右半平面调和映照的卷积
吴东东, 陈行堤
(华侨大学 数学科学学院, 福建 泉州 362021)

右半平面调和映照的卷积
吴东东, 陈行堤
(华侨大学 数学科学学院, 福建 泉州 362021)

调和映照; 卷积; 凸映照; 单叶性判别; 几何特征;Cohn法则
1 预备知识




两个调和映照的卷积映照的单叶性判别得到不少学者的研究[3-9].Dorff[5]证明了如下定理.

Dorff等[6]证明了如下的引理以及两个定理.



2 主要结果及证明

式(3)中:-A,-B,-C是三次多项式
的3个根(A,B,C可能相等).



下面引用Cohn法则[10]的引理B.

证明 假设-A,-B,-C是式(4)的3个根,则有
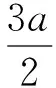
从而有|ABC|=|a/2|≤1/2<1,即-A,-B,-C这3个根中至少有一个根在单位圆盘D内.
当a∈(0,1]时,由t(z)可构造



所以有|-3a2/4-a/2+1|<|1-a2/4|.再应用t1(z)可构造


当a∈(0,1]时,有
(-2+2a+a2)2-(-4+a+2a2)2=-3(a+1)(a-1)(a+2)(a-2)≤0.

另外,当a=0时,第二复伸张w(z)=-z2为定理B中θ=π,n=2的特殊情形.因此,a∈[0,1]时定理1成立.

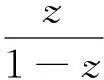
对h+g=z/(1-z)进行求导,可得
进一步对h′,g′求积分可得

而且有
通过Mathematica软件,f和f0*f分别把单位圆盘映成的图像,如图1所示.

(a) f (b) f0*f 图1 单位圆盘映成的图像Fig.1 Mapping unit disk onto domains
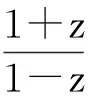
因此,可得
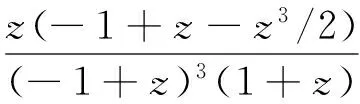
类似的有
所以有

[1] LEWY H.On the nonvanishing of the Jacobian in certain one-to-one mappings[J].Bulletin of the American Mathematical Society,1936,42(10):689-692.
[2] CLUNIE J G,SHEIL-SMALL T.Sheil-small, harmonic univalent functions[J].Annales Academi Scientiarum Fennic Series A I,1984,9(1):3-25.
[3] PONNUSAMY S,SINGH V.Convolution properties of some classes of analytic functions[J].Journal of Mathematical Sciences,1998,89(1):1008-1020.
[4] KUMAR R,DORFF M,GUPTA S,etal.Convolution properties of some harmonic mappings in the right half-plane[J].Bulletin of the Malaysian Mathematical Sciences Society,2016,39(1):439-455.
[5] DORFF M.Convolutions of planar harmonic convex mappings[J].Complex Variables Theory and Application An International Journal,2001,45(3):263-271.
[6] DORFF M,NOWAK M,WOLOSZKIEWICZ M.Convolutions of harmonic convex mappings[J].Complex Variables and Elliptic Equations,2012,57(5):489-503.
[7] LI Liulan,PONNUSAMY S.Solution to an open problem on convolutions of harmonic mappings[J].Complex Variables and Elliptic Equations,2013,58(12):1647-1653.
[8] JIANG Yueping,RASILA A,SUN Yong.A note on convexity of convolutions of harmonic mappings[J].Bulletin of the Korean Mathematical Society,2015,52(6):1925-1935.
[9] LI Liulan,PONNUSAMY S.Convolutions of slanted half-plane harmonic mappings[J].Analysis (Munich),2013,33(2):159-176.
[10] RAHMAN Q I,SCHMEISSER G.Analytic theory of polynomials, London mathematical society monographs new series[M].Oxford:Oxford University Press,2002:375-376.
(责任编辑: 钱筠 英文审校: 黄心中)
Convolution of Harmonic Mapping in Right-Half Plane
WU Dongdong, CHEN Xingdi
(School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China)

harmonic mapping; convolution; convex mapping; univalent criterion; geometric properties; Cohn′s rule
10.11830/ISSN.1000-5013.201703026
2016-09-05
陈行堤(1976-),男,教授,博士,主要从事函数论的研究.E-mail:chxtt@hqu.edu.cn.
国家自然科学基金资助项目(11471128); 福建省自然科学基金资助项目(2014J01013); 华侨大学中青年教师科研提升计划项目(ZQN-YXl10); 华侨大学研究生科研创新能力培育计划项目(2016年度)
O174.55
A
1000-5013(2017)03-0430-05

