离散多智能体系统分组一致性分析

林瑜阳， 李钟慎

(华侨大学 机电及自动化学院， 福建 厦门 361021)

离散多智能体系统分组一致性分析

林瑜阳， 李钟慎

(华侨大学 机电及自动化学院， 福建 厦门 361021)

在有向拓扑结构下，研究离散多智能体系统的分组一致问题，提出无入度平衡假设条件的控制协议设计方法.首先，根据系统模型，设计离散多智能体系统的分组一致控制协议.其次，利用代数图论和矩阵论，分析并得到离散多智能体系统实现分组一致的充要条件.最后，仿真结果验证了理论分析结论的正确性.数值仿真结果表明:系统实现分组一致仅要求有向图Gn含有一个有向生成树，不要求拓扑结构满足入度平衡条件.

多智能体系统； 离散时间系统； 入度平衡； 分组一致性

自然界中生物群体的群集现象，如蚂蚁聚集、大雁编队飞行等，均呈现出整体一致行为.多智能体一致性问题来源于自然界的群集现象，是指系统中所有个体通过局部间的彼此通信，最终状态收敛至一个值.一致性问题的研究可揭示生物群集现象的内在规律，解释生物群体行为[1-2].同时，由于多智能体系统比单一系统更具有灵活性、经济性，其一致性的研究在无人机编队控制、通信网络拥塞控制、机器人设计和搜索优化等领域得到广泛地应用[3-5].近年来，多位学者从智能体动态模型、通信拓扑和一致性协议等3个基本方面对一致性问题展开大量研究[6-10].考虑实际问题的复杂性，个体的最终状态往往不能收敛至一个值.当个体最终状态收敛至多个值时，一致性问题转化为分组一致问题，分组一致问题是一致性问题的推广，在理论研究上也具有重要意义[11-18].然而，相关的研究均基于入度平衡假设条件展开，忽略了组间彼此影响.本文研究无入度平衡条件下离散多智能体系统的分组一致问题，提出分组一致控制策略，得到实现分组一致的充要条件，并通过数值仿真验证所得结论的正确性.

1 预备知识与问题描述

考虑具有n个智能体的系统，智能体之间的通信拓扑可用有向图G={V,E}表示.其中，节点集合V={v1,v2,…,vn}；边集合E⊆V×V.节点vi的邻居集合为Ni={vj∈V：(vi,vj)∈E}.图G的邻接矩阵A={ai,j}∈Rn×n.其中，矩阵元素ai,j为与有向边(vi,vj)对应的连接权重.当(vi,vj)∈E时，ai,j>0；反之，ai,j=0.如果(vi,vj)∈E，则表示从节点vi有一条有向路径指向节点vj，节点vi称为父节点，节点vj称为子节点.如果有向图中除了一个节点(根节点)没有父节点外，其余每个节点有且仅有一个父节点，且根节点可以通过一条有向路径到达其余所有节点，则称该图为有向树.当一个有向图中的有向树含有与该图相同的节点集，则称该有向树为有向图的有向生成树.在包含多个分组的多智能体系统中，节点入度平衡条件要求一个分组中每个节点到其他分组中所有节点的邻接权重和等于零.

包含n个智能体的一阶离散系统模型为

式(1)中:k∈{0,1,…}为离散时间序列;xi∈Rm,ui∈Rm分别表示第i个智能体的状态及控制输入.不失一般性，设m=1，对于m>1的情况，通过Kronecker算子容易进行扩展.

考虑系统(1)，假设{X1,X2,…,Xp}为所有智能体的一个分割，给出如下分组一致的定义.

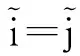
针对一阶离散多智能体系统(1)，设计包含p个分组的一致性协议,即

(2)

(3)

2 主要结果

针对离散多智能体系统，分析在一致性协议(2)下实现分组一致需满足的充要条件.首先，给出若干引理.

引理1[19]设矩阵A=[ai,j]∈Rn×n，令

|ai,j|,i=1,2,…,n，

表示矩阵A的去心绝对行和，则A的所有特征值都落在n个圆盘的区域G(A)中，其中,

|z-ai，i|

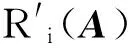
定理1 设非负矩阵A=[ai,j]∈Rn×n具有相同恒定正行和，则μ为矩阵A的一个特征值，对应的特征向量为1n，且矩阵A的谱半径ρ(A)=μ.当且仅当矩阵A对应的有向图G(A)含有一个有向生成树时，特征值μ的代数重数为1.若ai,i>0，i=1,2,…,n，则对所有λ≠μ的特征值，|λ|<μ.如果G(A)含有一个有向生成树，且ai,i>0，i=1,2,…,n，则μ为矩阵A的最大特征单根.

证明 定理第1部分，矩阵A具有相同恒定正行和μ，即有A1n=μ1n，μ为矩阵A的一个特征值，对应的特征向量为1n，由引理1可知，A的所有特征值都落在n个圆盘的区域G(A)中，圆盘区域G(A)为

|z-ai，i||ai,j|

定理第2部分，需对充要性进行论证.

设矩阵B=A-μIn，有λi(A)=λi(B)+μ，i=1,2,…,n,λi(·)表示第i个特征值.若矩阵A对应的有向图G(A)含有一个有向生成树，则B对应的有向图G(B)也含有一个有向生成树.又因为矩阵B满足引理2的条件，可知B具有一个代数重数是1的零特征值，即矩阵A具有代数重数为1的特征值μ.

矩阵A的特征值μ的代数重数为1，假设A对应的有向图G(A)不含有一个有向生成树，由引理2可知，矩阵B=A-μIn的零特征值个数不为1，即矩阵A特征值μ的个数不为1，与条件矛盾，因此，有向图G(A)含有一个有向生成树.

定理第3部分，如果ai,i>0，易知集合(4)包含于圆形区域{z∈：|z|=μ}中，且n个圆盘的边界仅在z=μ处与圆形区域有一个交点.因此，对A的所有λ≠μ的特征值，均有|λ|<μ.

由定理第2部分和第3部分，可直接得到第4部分的结论.

推论1 设随机矩阵A=[ai,j]∈Rn×n，当且仅当A对应的有向图G(A)含有一个有向生成树时，矩阵A具有代数重数为1的特征值λ=1，且ρ(A)=1.若ai,i>0,i=1,2,…,n，则对所有非1特征值而言，|λ|<1.如果G(A)含有一个有向生成树，ai,i>0,i=1,2,…,n，则λ=1为随机矩阵A的最大特征单根.

引理4[19]如果矩阵A∈Rn×n是非负的，则谱半径ρ(A)是A的一个特征值，且存在一个正向量x>0，使Ax=ρ(A)x.

对离散多智能体系统

的一致性分析有如下引理.

引理5 当且仅当

时，离散时间算法(5)可实现渐进一致.其中，A=[ai,j]∈Rn×n是一个随机矩阵;当k→∞时，c是一个n阶常系数列向量.

证明 当节点vi和vj位于相同分组时，令ej,i，对系统(3)有

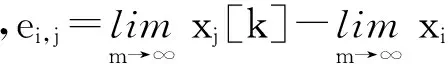
(8)

系统(3)实现分组一致即等价于系统(8)实现一致.现对系统(8)进行一致性证明.

综上，当且仅当有向图Gn含有一个有向生成树时，系统(8)可实现一致，即系统(3)可实现分组一致.定理得证.

3 数值仿真

结合具体实例进行数值仿真，以验证所得结论的正确性.

实验1 具有5个智能体2个分组的系统，如图1所示.其中,C1={1,2};C2={3,4,5}.易知系统含有一个有向生成树，且不满足入度平衡条件，其随机矩阵A和组关联矩阵E分别为

智能体初始状态x(20)=[3 5 0 4 6]T,在一致性协议(2)下,系统经k=20步响应后,智能体状态为x(20)=[3.2581 3.2581 2.2581 1.2580 1.2581]T,状态响应过程,如图2所示.图2中:x(k)为智能体状态;k 为离散时间序列.

图1 系统通信拓扑图 图2 系统的状态响应Fig.1 Communication topology of system Fig.2 State response of system

由图2可知：在一致性协议(2)下，对于图1的系统，离散智能体状态随着时间的增加趋于分组一致，收敛值关系与组关联矩阵对应，仿真结果与理论分析结果相吻合.

实验2 现将智能体数目扩充至8个，组数扩充至3个，其拓扑结构如图3所示.其中，C1={1,2};C2={3,4,5};C3={6,7,8}.系统含有一个有向生成树，同样不满足入度平衡条件，其随机矩阵A和组关联矩阵E分别为

智能体初始状态x(0)=[1 2 3 4 5 6 7 8]T,在一致性协议(2)下,经过k=30步响应,智能体状态为x(30)=[6.6530 6.6423 4.6530 4.6530 4.6530 3.6450 3.65303.6530]T,状态响应过程,如图4所示.

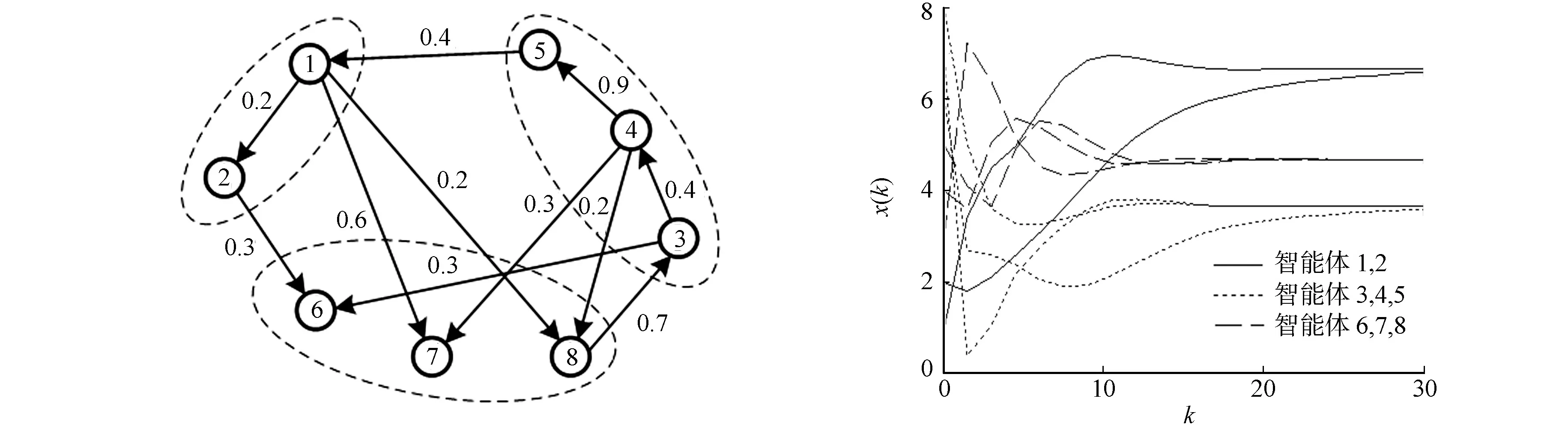
图3 系统通信拓扑图 图4 系统的状态响应 Fig.3 Communication topology of system Fig.4 State response of system

由图4可知：在一致性协议(2)下，对于离散多智能体系统，随着时间的增加，智能体状态趋于分组一致，且收敛值之间的关系与组关联矩阵相对应，进一步验证了理论分析结果的正确性.此外，结合实验1和实验2可知，系统能否实现分组一致与智能体个数无关.

4 结束语

研究无入度平衡条件下的离散多智能体系统分组一致问题.通过引入个体收敛值之差，设计离散多智能体分组一致协议，并利用图论和矩阵论的方法，得到系统实现分组一致的充要条件.数值仿真结果表明:系统实现分组一致仅要求有向图Gn含有一个有向生成树，不要求拓扑结构满足入度平衡条件.

[1] COUZIN I D,KRAUSE J,JAMES R,etal.Collective memory and spatial sorting in animal groups[J].Journal of Theoretical Biology,2002,218(1):1-11.

[2] PARRISH J K,VISCIDO S V,GRUNBAUM D.Self-organized fish schools: An examination of emergent properties[J].Biology Bull,2002,202(2):296-305.

[3] 唐贤伦,张衡,周家林,等.基于多Agent混沌粒子群优化的磁悬浮系统PID控制器[J].信息与控制,2013,42(6):758-764.

[4] WERFEL J,PETERSEN K,NAGPAL R.Designing collective behavior in a termite-inspired robot construction team[J].Science,2014,343(6172):754-758.

[5] SHARMA A,SRIVASTAVA S C,CHAKRABARTI S.Multi-agent-based dynamic state estimator for multi-area power system[J].IET Generation, Transmission and Distribution,2016,10(1):131-141.

[6] VICSEK T,CZIROOK A,BEN-JACOB E,etal.Novel type of phase transition in a system of self-driven particles[J].Physical Review Letters,1995,75(6):1226-1229.

[7] OLFATI-SABER R,MURRAY R M.Consensus problems in networks of agents with switching topology and time-delays[J].IEEE Transactions on Automatic Control,2004,49(9):1520-1533.

[8] XIE Guangming,WANG Long.Consensus control for a class of networks of dynamic agents[J].International Journal of Robust and Nonlinear Control,2007,17(10/11):941-959.

[9] YU Wenwu,CHEN Guanrong,CAO Ming,etal.Second-order consensus for multi-agent systems with directed topologies and nonlinear dynamics[J].IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics,2010,40(3):881-891.

[10] 许耀赆,田玉平.线性及非线性一致性问题综述[J].控制理论与应用,2014,31(7):837-849.

[11] YU Junyan,WANG Long.Group consensus in multi-agent systems with switching topologies and communication delays[J].System and Control Letters,2010,59(6):330-348.

[12] YU Junyan,WANG Long.Group consensus of multi-agent systems with undirected communication exchange[J].International Journal of Systems Science,2012,43(2):334-348.

[13] 王强,王玉振,杨仁明.一类多智能体系统分组一致控制协议的设计与分析[J].控制与决策,2013,28(3):369-373，378.

[14] XIA Hong,HUANG Tingzhu,SHAO Jinliang,etal.Group consensus of multi-agent systems with communication delays[J].Neurocomputing,2016(171):1666-1673.

[15] XIA Weiguo,CAO Ming.Clustering in diffusively coupled networks[J].Automatica,2011,47(11):2395-2405.

[16] WANG Yuzhen,ZHANG Chenghui,LIU Zhenbin.A matrix approach to graph maximum stable set and coloring problems with application to multi-agent system[J].Automatica,2012,48(7):1227-1236.

[17] 纪良浩,廖晓峰,刘群.时延多智能体系统分组一致性分析[J].物理学报,2012,61(22):5-12.

[18] QIN Jiahu,YU Changbin.Cluster consensus control of generic linear multi-agent systems under directed topology with acyclic partition[J].Automatica,2013,49(2):2898-2905.

[19] HORN R A,JOHNSON C R.Matrix analysis[M].Cambridge:Cambridge University Press,1985:344,498,503.

(责任编辑： 钱筠 英文审校： 崔长彩)

Group Consensus Analysis of Discrete-Time Multi-Agent Systems

LIN Yuyang, LI Zhongshen

(College of Mechanical Engineering and Automation, Huaqiao University, Xiamen 361021, China)

In this paper, the protocol design method without in-degree balanced assumption was presented under the directed graph topology to investigate the grouping consensus problem for a class of discrete-time multi-agent systems. Firstly, based on the model of discrete-time multi-agent systems, a grouping consensus protocol was designed. Then, according to the algebraic graph theory and the matrix theory, the grouping consensus problem was studied. The sufficient and necessary condition of group consensus for the discrete-time multi-agent systems was obtained. Finally, simulation results demonstrated that the grouping consensus of the systems only required that the directed graphGnhad a direct spanning tree however the in-degree balanced assumption was not necessary. Keywords：multi-agent systems; discrete-time systems; in-degree balanced; group consensus

10.11830/ISSN.1000-5013.201703005

2016-04-11

李钟慎(1971-)，男，教授，博士，主要从事先进控制理论与控制工程的研究.E-mail:lzscyw@hqu.edu.cn.

福建省自然科学基金资助项目(2013J05077)； 中央高校基本科研业务基金资助项目(JB-ZR1107)； 福建省厦门市集美区科技计划项目(20137C01)； 华侨大学研究生科研创新能力培育计划项目(2014年度)

TP 273

A

1000-5013(2017)03-0306-06