可产生多翼吸引子的混沌系统及其电路实现
胡春华, 王忠林, 王春梅, 孙平
(1. 滨州学院 电气工程系, 山东 滨州 256603;2. 山东师范大学 物理与电子科学学院, 山东 济南 250014;3. 滨州学院 航空工程学院, 山东 滨州 256603;4. 滨州学院 信息工程学院, 山东 滨州 256603)

可产生多翼吸引子的混沌系统及其电路实现
胡春华1,2, 王忠林3, 王春梅4, 孙平2
(1. 滨州学院 电气工程系, 山东 滨州 256603;2. 山东师范大学 物理与电子科学学院, 山东 济南 250014;3. 滨州学院 航空工程学院, 山东 滨州 256603;4. 滨州学院 信息工程学院, 山东 滨州 256603)
构造一个只有一个零平衡点的新混沌系统,与广义Lorenz系统族相比,该系统可以产生单、双、三及四翼的混沌吸引子.研究表明:当参数d=2时,其平衡点为鞍结点;当参数d=5时,其平衡点为鞍焦点,且系统的散度随着参数d的变化而改变,不是一个固定值.在Multism 12仿真平台上设计该系统的电子电路,仿真结果与数值仿真、动力学特性分析结论一致,进一步验证该混沌系统的混沌特性.
混沌系统; 多翼吸引子; 电子电路; Lyapunov指数; Multism 12平台
自1963年Lorenz发现第一个混沌吸引子[1]以来,作为非线性科学的一个重要分支——混沌理论引起了国内外研究者的广泛关注,有目的地产生新型混沌系统成为研究的热点.利用混沌反控制方法,Chen等[2]构造了Chen系统,Lü等构造了Lü系统[3],其他研究者也构造了新型混沌系统,如Liu系统[4]等.这类系统称为广义的Lorenz混沌系统族[5-8].在广义Lorenz混沌系统族的基础上通过增加饱和函数或正弦函数等方法,可以构造多翼混沌系统.但采用这种方法构造的多翼混沌系统,一方面,要增加系统的平衡点,另一方面,系统具有某种对称性,即出现四翼、八翼等,比较难出现如三翼、六翼等[9-14].本文构造了一个新的混沌系统,与广义Lorenz系统族相比,它可以产生单翼、双翼、三翼及四翼混沌吸引子,具有更加丰富的动力学特性.
1 混沌系统模型
文中提出的混沌系统模型为
式(1)中:x,y,z为状态变量;d为系统参数.
当d等于2.0,3.0,3.6,5.0时,系统(1)产生单翼、双翼、三翼和四翼的吸引子,相图如图1所示.

(a) x-y平面(d=2.0) (b) x-z平面(d=2.0)

(c) y-z平面(d=2.0) (d) x-y平面(d=3.0)

(e) x-z平面(d=3.0) (f) y-z平面(d=3.0)

(g) x-y平面(d=3.6) (h) x-z平面(d=3.6)
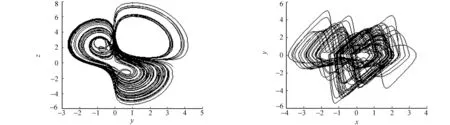
(i) y-z平面(d=3.6) (j) x-y平面(d=5.0)

(k) x-z平面(d=5.0) (l) y-z平面(d=5.0)图1 混沌系统(1)的混沌吸引子在相平面上的投影Fig.1 Phase portraits of chaotic attractors of chaotic system (1)
2 混沌系统的特性分析
2.1 对称性
系统(1)关于y=-x对称,即做变换(x,y,z)→(-x,-y,-z)后,系统保持不变,这与一般混沌系统关于Z轴对称不同.
2.2 耗散性
因为有
因此,系统(1)的散度不一定总小于0,故直接决定系统(1)的散度是比较困难的.这与一般具有散度小于零的混沌系统有着显著的不同.
2.3 平衡点及稳定性
由此可解得系统(1)只有一个平衡点S(0,0,0).
在平衡点S(0,0,0),线性化系统(2)得其Jacobian矩阵为
令det(J-λI)=0,可解得Jacobian矩阵的特征方程为

1) 当d=2.0时,解得相应的特征根λ1=-1,λ2,3=0.333 3±0.471·i;
2) 当d=3.0时,解得相应的特征根λ1,λ2,3=0.5±0.288 7·i,特征根λ1为负实根,λ2,3是一对具有正实部的共轭复根,根据Routh-Hurwitz条件,这时平衡点S(0,0,0)是不稳定鞍焦点;
3) 当d=3.6时,解得相应的特征根λ1=-1,λ2=0.763 3,λ3=0.436 7;
4) 当d=5.0时,解得相应的特征根λ1=-1,λ2=1.434 3,λ3=0.232 4,特征根不全为正或负,根据Routh-Hurwitz条件,这时平衡点S(0,0,0)是不稳定鞍结点.
2.4 Lyapunov指数和Lyapunov维数
1) 当d=2.0时,计算得系统(1)的Lyapuvnov指数分别为LE1=0.048 4,LE2=0,LE3=-0.395,则系统(1)的Lyapunov维数为
这时系统产生单翼混沌吸引子.
2) 当d=3.0时,可得系统(1)的Lyapuvnov指数分别为LE1=0.048 4,LE2=0,LE3=-0.276 2,系统(1)的Lyapunov维数为
这时系统产生双翼混沌吸引子.
3) 当d=3.6时,可得系统(1)的Lyapuvnov指数分别为LE1=0.028 6,LE2=0,LE3=-0.244 3.系统(1)的Lyapunov维数为
这时系统产生三翼混沌吸引子.
4) 当d=5.0时,计算得系统(1)的Lyapuvnov指数分别为LE1=0.077 8,LE2=0,LE3=-0.244.系统(1)的Lyapunov维数为
这时系统产生四翼混沌吸引子.
系统(1)具有一个正的Lyapunov指数,且其Lyapunov维数是分数,因而系统(1)是混沌的.
3 系统的电路实现
文中用线性电阻、电容、模拟乘法器和运算放大器设计了一个模拟电路系统,以实现所提出的新混沌系统(1),其实现电路如图3所示.采用模拟乘法器AD633JN,实现系统中非线性乘积项的乘法运算;运算放大器选用LF347N,其电源电压VCC=15 V,VEE=-15 V,输出饱和值Vsat=±13.5 V,它分别与电容、线性电阻组合实现积分、加减和反相等运算.

图2 混沌系统(1)的电路实现Fig.2 Circuit of implemented chaotic system (1)
通过在Multism 12仿真平台上运行图2所示的电路系统,并借助于虚拟示波器分别得到了当d等于2.0,3.0,3.6,5.0时的相图,如图3所示.

(c) 三翼 (d) 四翼图3 混沌系统(1)的混沌吸引子的仿真分析Fig.3 Experimental observation of chaotic attractor of chaotic system (1)
由图3可知:与数值仿真相比,所获得的结果与数值仿真非常接近,这说明系统(1)中存在的混沌吸引子可以通过实际电路实现.
4 结束语
提出一个新的混沌系统,与己有混沌系统相比较,该系统只有一个零平衡点,并且在不同参数下零平衡点性质不同,可以产生单、双、三及四翼混沌吸引子,具有更加丰富的动力学特性.此外,系统是关于y=-x对称的,其散度不是常数.该混沌系统在较大的参数范围内具有复杂的动力学特性,在通信的同步控制和图像处理方面更具有理论和工程应用价值.
[1] LORENZ E N.Deterministic non-perodic flows[J].Atoms Sci,1963,20:130.
[2] CHEN Guangrong,UETA T.Yet another chaotic attractor[J].International Journal of Bifurcation and Chaos,1999,9(7):1465-1466.
[3] LYU Jinhu,CHEN Guangrong.A new chaotic attractor coined[J].International Journal of Bifurcation and Chaos,2002,12(3):659-661.
[4] LIU Chongxin,LIU Tao,LIU Ling,etal.A new chaotic attracator[J]. Chaos Solitons and Fractals,2004,22(2):1031-1038.
[5] 蔡国梁,谭振梅,周维怀,等.一个新的混沌系统的动力学分析及混沌控制[J].物理学报,2007,56(11):6230-6237.
[6] 王忠林.一个混沌系统设计及其FPGA实现[J].滨州学院学报,2008,24(6):89-93.
[7] 吴淑花,刘振永,张若洵,等.一个新三维系统的电路实现及其混沌控制[J].重庆邮电大学学报(自然科学版),2012,24(4):473-478.
[8] 黄沄,罗小华,张鹏.一种新的具有光滑二次函数多涡卷混沌系统及其FPGA实现[J].重庆邮电大学学报(自然科学版),2012,24(4):479-482.
[9] 乔晓华,包伯成.三维四翼广义增广Lü系统[J].物理学报,2009,58(12):8152-8159.
[10] WANG Guangyi,QIU Shuisheng,LI Hongwei.A new chaotic system and its circuit realization[J].Chinese Physics B,2006,15(12):2872-2877.
[11] 王忠林,姚福安,李祥峰.基于FPGA的一个超混沌系统的设计与实现[J].山东大学学报(理学版),2008,43(12):89-91.
[12] 王杰智,陈增强,袁著祉.一个新的混沌系统及其性质研究[J].物理学报,2006,55(8):3956-3963.
[13] LYU Jinhu,CHEN Guangrong,CHENG Dong,etal.Bridge the gap between the Lorenz and the Chen system[J].International Journal of Bifurcation and Chaos,2002,12(12):2917-2926.
[14] LYU Jinhu,CHEN Guangrong,ZHANG Suochun.Controlling in between the Lorenz and the Chen system[J].Theological Studies in Japan,2011,21(2):77-79.
(责任编辑: 钱筠 英文审校: 崔长彩)
Construction of Chaotic System With Multi-Winged Attractors and Its Circuit Implementation
HU Chunhua1,2, WANG Zhonglin3, WANG Chunmei4, SUN Ping2
(1. Department of Electronics Engineering, Binzhou University, Binzhou 256603, China;2. School of Physics and Electronics, Shandong Normal University, Jinan 250014, China;3. College of Aeronautical Engineering, Binzhou University, Binzhou 256603, China;4. College of Information Engineering, Binzhou University, Binzhou 256603, China)
A novel chaotic system with single zero-balanced point is constructed in this research. The system is different from the generalized Lorenz system with its divergence, symmetry and the stability of zero-balanced point. The new system is able to produce single-winged, double-winged, three-winged and four-winged chaotic attractors. In addition, a simulation circuit of the system is designed to implement the proposed system. The circuit simulation results are inagreement with numerical simulation and dynamic analysis, which verifies the chaotic characteristics of the proposed system. Keywords:chaotic system; multi-winged attractor; electronic circuit; Lyapunov index; Multism 12 simulation platform
10.11830/ISSN.1000-5013.201703004
2016-11-16
胡春华(1979-),女,副教授,博士,主要从事EDA技术与混沌理论应用的研究.E-mail:bzhuchunhua@126. com.
山东省自然科学基金资助项目(ZR2014FQ019); 山东省滨州市科技发展计划项目(2014ZC0208); 滨州学院科研基金资助项目(BZXYG1618)
TN 914.42
A
1000-5013(2017)03-0300-06

