马铃薯泥鼓风冷冻数值模拟与实验
万金庆 岳占凯 厉建国 王友君
(上海海洋大学食品学院, 上海 201306)
马铃薯泥鼓风冷冻数值模拟与实验
万金庆 岳占凯 厉建国 王友君
(上海海洋大学食品学院, 上海 201306)
为掌握马铃薯泥在鼓风冷冻过程中的温度变化规律,建立了短圆柱状马铃薯泥鼓风冷冻的三维数值模型,进行了三维非稳态数值模拟,并结合流场及不同时刻的温度场对马铃薯泥的冷冻过程进行了分析。实验验证表明该模型与实际情况吻合较好,冷冻时间相对误差为3.9%。以此为基础,研究了送风速度和温度对马铃薯泥冷冻过程的影响。结果表明,随着风速的提高,冷冻时间缩短,马铃薯泥内外温差增大,冷冻结束时马铃薯泥中心温度之间的差异先减小后增大。降低送风温度可以缩短冷冻时间,增大马铃薯泥中心温度之间的差异性和马铃薯泥内外温差。送风速度和温度对相变阶段的影响大于预冷段和深冷段。
马铃薯泥; 鼓风; 冷冻时间; 降温特性; 数值模拟
引言
冷冻食品质量很大程度上取决于食品的冻结速度。研究者从冰晶在食品组织中的形成这一角度对食品的快速冷冻和慢速冷冻进行了研究[1-3]。准确预测食品的冷冻时间对优化冷冻装置、降低生产能耗具有关键作用[4-6]。数值计算方法将食品热物性参数与冷冻过程的流体力学特性相结合,在预测食品冷冻时间方面比其它传统方法更加准确可靠,而且应用方便,节约时间和经费。目前,食品冷冻数值计算的主要研究方向有2个:一个是食品冷冻数学模型的研究,包括不同数值离散方法的使用,相变潜热、热质耦合、水分转移和应力变化的处理等,这些研究扩大了数值计算方法在食品冷冻领域的适用范围,提高了计算结果的准确性。文献[7]对以上内容作了较为详细的论述。另一个研究方向是食品冷冻数学模型的应用,包括预测食品冷冻时间、冷冻速率、干耗、传递系数、不同冷冻时刻的温度场和流场等[8-11]。根据模拟结果,可以优化食品冷冻工艺和冷冻设备,提高冻品质量,降低能耗。
食品冷冻数值模型大多用于预测单体食品的冷冻时间和降温特性,而在实际生产中,往往是大量食品按批次进行冷冻处理,因此,对多个食品同时进行冷冻模拟更具实际意义。本文以规则排列的多个无包装短圆柱状马铃薯泥的冷冻过程为研究对象,建立三维数值模型,使用Gambit软件对模型实体进行网格划分,Fluent 软件对模型进行求解,研究马铃薯泥冷冻过程中的降温特性,并通过实验验证该模型的准确性,为相关冷冻过程的研究与优化提供参考。
1 物理模型
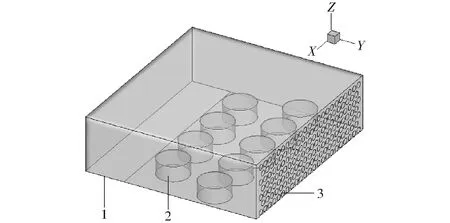
图1 食品与厢体三维模型Fig.1 Three-dimensional model of food and freezing room1.回风口 2.马铃薯泥 3.均流板进风口
本文主要研究短圆柱状无包装马铃薯泥冷冻降温特性,以鼓风冷冻装置(Pr.c-15型普龙通高效保鲜冷冻机)和马铃薯泥组成的整体(图1)为研究对象。厢体内部空间尺寸(长×宽×高)为600 mm×555 mm×180 mm,厢体内胆、外壳材料为不锈钢,绝热材料为氨基甲酸乙酯。圆柱状马铃薯泥高50 mm、直径100 mm,共9个,分两排布置。进风口均流板孔直径20 mm,回风口尺寸(长×宽)为600 mm×125 mm。
使用Gambit建立三维实体模型,采用非结构化网格划分方法,网格类型为Tet/Hybrid混合网格。流体区域网格尺寸为15 mm,马铃薯泥区域网格尺寸为5 mm,整体网格数量为225 290。
2 数学模型
为了计算方便,建模时做如下假设:马铃薯泥初始温度分布均匀,各向同性且质地均匀;马铃薯泥内部热交换只考虑导热,忽略对流换热;忽略马铃薯泥表面水分蒸发和内部水分转移对换热过程的影响;忽略马铃薯泥表面和厢体壁面之间的辐射换热;厢体密封性良好,不存在漏气现象;厢体内空气近似为不可压缩流体,符合Boussinesq假设。
2.1 食品传热微分方程
基于上述假设,将马铃薯泥的冷冻过程视为一个无内热源的变物性、非稳态导热问题,直角坐标系下的三维数学模型为[12]
(1)
式中T——马铃薯泥各几何点处温度,Kt——时间,sCp——马铃薯泥比热容,kJ/(kg·K)k——马铃薯泥导热系数,W/(m·K)ρ——马铃薯泥密度,kg/m3
马铃薯泥的顶面和侧面与冷冻装置内的冷风发生强制对流换热,视为第三类边界条件[12],即
(2)
式中w——边界符号n——马铃薯泥表面外法线方向h——马铃薯泥表面对流换热系数,W/(m2·K)Tw——马铃薯泥表面温度,KText——冷风温度,K
在Fluent软件中,马铃薯泥(固体)与空气(流体)的接触面设为耦合面,耦合面的对流换热系数由软件自行计算。
马铃薯泥底面与托盘直接接触,托盘材料为不锈钢,冷冻过程中托盘温度假设与冷风温度相等,马铃薯泥底面温度近似为托盘温度,即Td=Text,Td为马铃薯泥底面温度。初始条件为T=T0,T0为马铃薯泥初始温度。
2.2 食品热物性参数
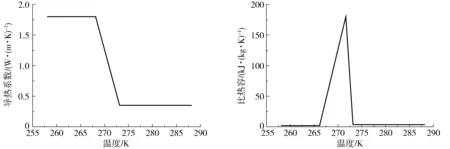
图2 食品冷冻过程热物性参数的典型变化过程Fig.2 Typical variation process of thermal properties with temperature
对于大多数食品的冷冻过程而言,相变并非发生在一个明确的温度上,而是发生在一个相对较小的温度范围之内。食品的比热容和导热系数等热物性参数在相变前后会发生很大的变化[13](图2)。本文通过8个独立的参数对马铃薯泥冷冻过程中的导热系数和比热容做分段线性化处理[14],公式为
(3)
式中Ts——马铃薯泥相变结束温度,KTl——马铃薯泥初始冻结温度,Kks——马铃薯泥冻结后导热系数,W/(m·K)kl——马铃薯泥冻结前导热系数,W/(m·K)
将处于相变段的导热系数作为温度的线性函数,预冷段和深冷段的导热系数设为常数。
(4)
式中Cs——马铃薯泥冻结后比热容,kJ/(kg·K)Cmax——马铃薯泥冻结过程中最大比热容,kJ/(kg·K)
Cl——马铃薯泥冻结前比热容,kJ/(kg·K)
Tmax——马铃薯泥冻结过程中最大比热容对应的温度,K
将预冷段和深冷段的比热容设为常数,相变段分两段,设为温度的线性函数。马铃薯泥的密度在整个冷冻过程中假定不变,取1 018 kg/m3。所提到的8个独立参数如表1所示[14]。
2.3 进风口、回风口边界及内壁
进风口设置为Velocity-inlet(速度入口),选用湍流强度和水力直径定义湍流,进风口风速4 m/s(热线风速仪实际测量值),温度243.15 K。回风口设置为Outflow(自由出流)。厢体壁面设置为绝热壁面。马铃薯泥与冷风接触的表面设置为耦合壁面,其对流传热系数由Fluent自行计算。
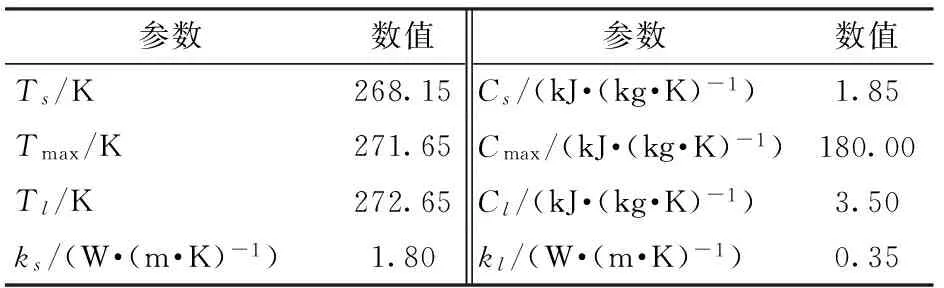
表1 马铃薯泥相关物性参数
3 模型求解与实验验证
3.1 模型求解
根据上述各项参数对模型进行设置。选用SSTk-ω紊流模型[15],采用基于压力的瞬态求解器对模型进行求解。初始时间步长设为0.01 s,待残差曲线收敛后逐渐增大时间步长至5 s,能量方程收敛精度设为10-6,其余方程收敛精度为10-3。以降温最慢的马铃薯泥几何中心温度达到255.15 K作为冷冻结束的标志。
3.2 模拟结果与分析
以厢体底面中心位置为坐标原点,沿Z轴方向取Z=25 mm截面流场速度分布云图,如图3所示。流场速度分布云图显示:气流在马铃薯泥的迎风面和背风面会出现附于其表面的现象,而且第1排5个马铃薯泥背风面风速滞止区明显大于第2排4个马铃薯泥背风面的风速滞止区;由于第1排的遮挡,第2排马铃薯泥周围风速均匀性要好于第1排,但是其被最大风速吹过的表面积明显小于第1排。
马铃薯泥在冷冻过程中经历预冷、相变、深冷3个阶段。根据冷冻降温曲线,分别选择40、140、190、200 min时Z=25 mm截面的温度场云图进行对比分析。
如图4所示,冷冻开始40 min时,所有马铃薯泥处于预冷段,降温较快,第2排马铃薯泥周围的温度场稍高于第1排,但两者的降温速度基本相等。140 min时,马铃薯泥处于相变段,迎风面降温明显快过背风面,而且第1排的降温速度比第2
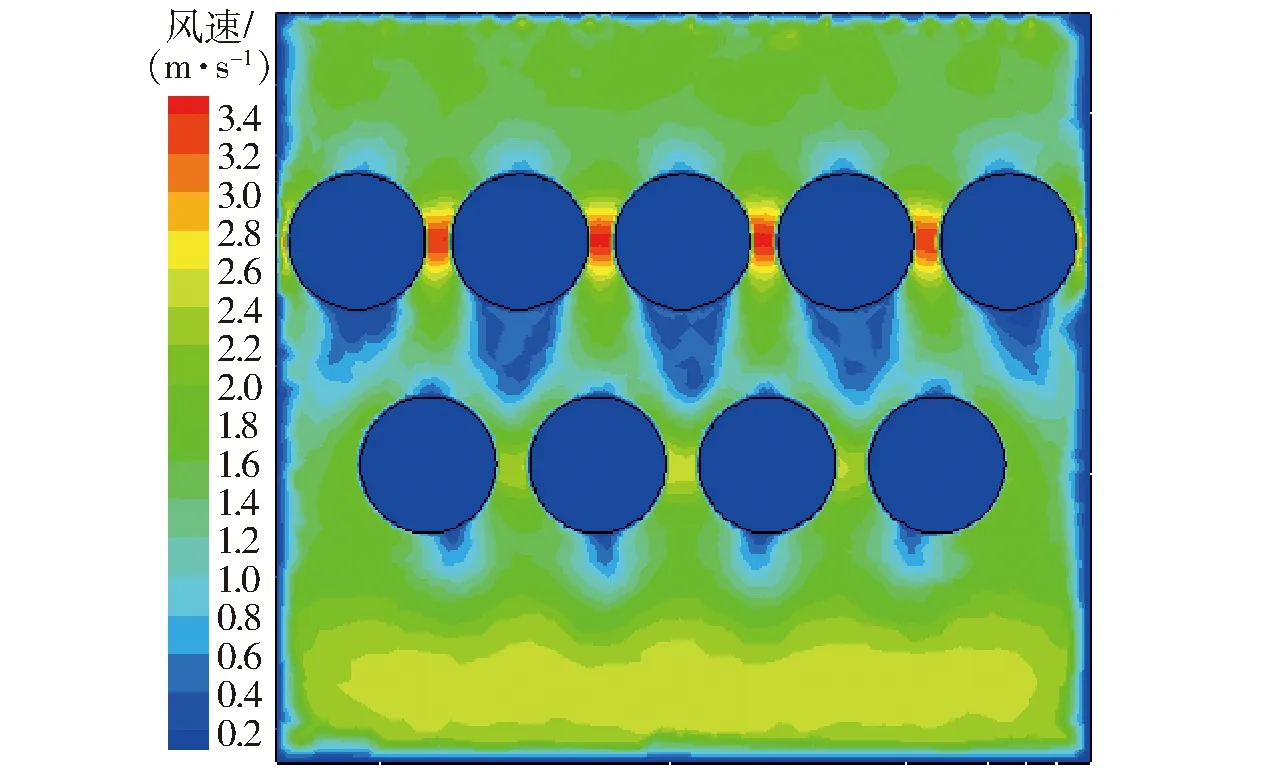
图3 流场速度云图Fig.3 Velocity contour in container
排快,二者周围温度场的差异性较40 min时减小,相变界面由外向内推进。190 min时,第1排马铃薯泥的相变完成,进入深冷段,只有两侧马铃薯泥的中心部分尚未降到255.15 K。处在深冷段的马铃薯泥,迎风面的降温速度依然快过背风面。第2排马铃薯泥的中心仍然处于相变阶段,而且热中心稍向背风面移动,第1排和第2排周围的温度场差异性进一步减小。200 min时,所有马铃薯泥热中心温度降到255.15 K,冷冻结束。第1排马铃薯泥的温度明显低于第2排,而且第1排的温度分布更加均匀。
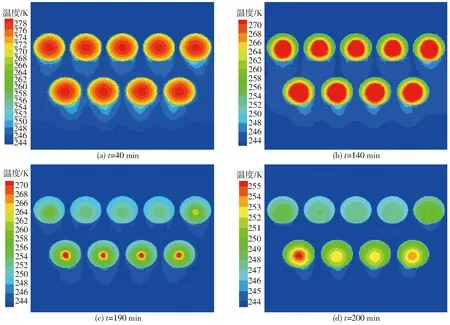
图4 不同冷冻时刻的二维温度场Fig.4 Contours of static temperature of freezing process
在预冷段,由于马铃薯泥与冷风之间温差较大,风速对降温速度的影响较小,使得迎风面与背风面之间的降温差异不够明显。在相变段和深冷段,风速对降温速度的影响增大,迎风面的降温速度快过背风面,使得马铃薯泥的热中心稍微向背风面偏移。虽然流场分布云图表明第2排马铃薯泥周围风速更加均匀,但这并没有加快它们的降温速度,由此可见,在马铃薯泥周围温度场基本相同的情况下,流场的均匀性对降温速度的影响小于流速对降温速度的影响,这与文献[16]得出的结论相吻合。
3.3 模型的实验验证
实验仪器:Agilent 34972A型数据采集仪,T型铜-康铜热电偶(外径1 mm,精度±0.3℃)。实验材料为自制马铃薯泥。热电偶插在马铃薯泥几何中心,当厢体内温度降到243.15 K并维持30 min后放入马铃薯泥,温度数据每隔10 s采集一次。冷冻结束时马铃薯泥如图5所示。以所有马铃薯泥几何中心的平均温度降到255.15 K所用的时间做冷冻曲线,实验结果与模拟结果的对比如图6所示。

图5 冷冻结束时马铃薯泥Fig.5 Frozen mashed potatoes
在预冷段、相变段、深冷段的最大温度误差为1.5、2.7、7.1 K,分别发生在28、188、198 min。冷冻时间的模拟值为198 min,实验值为206 min,冷冻时间相对误差为3.9%。结果证明,该模型具有一定的准确性。
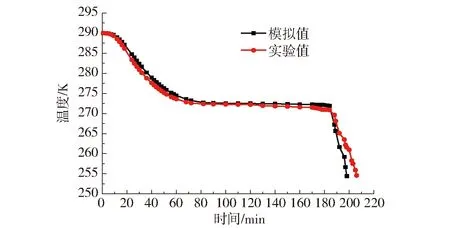
图6 马铃薯泥中心平均温度实验值与模拟值的比较Fig.6 Comparison of simulated and test temperatures during freezing
4 设计参数对冷冻过程的影响
4.1 送风速度对冷冻过程的影响
风速是影响食品冷冻时间的关键因素之一[17]。进风口风速分别为2、4、6、8、10 m/s时,马铃薯泥平均中心温度的变化曲线如图7所示,相应的各阶段降温时间如表2所示。
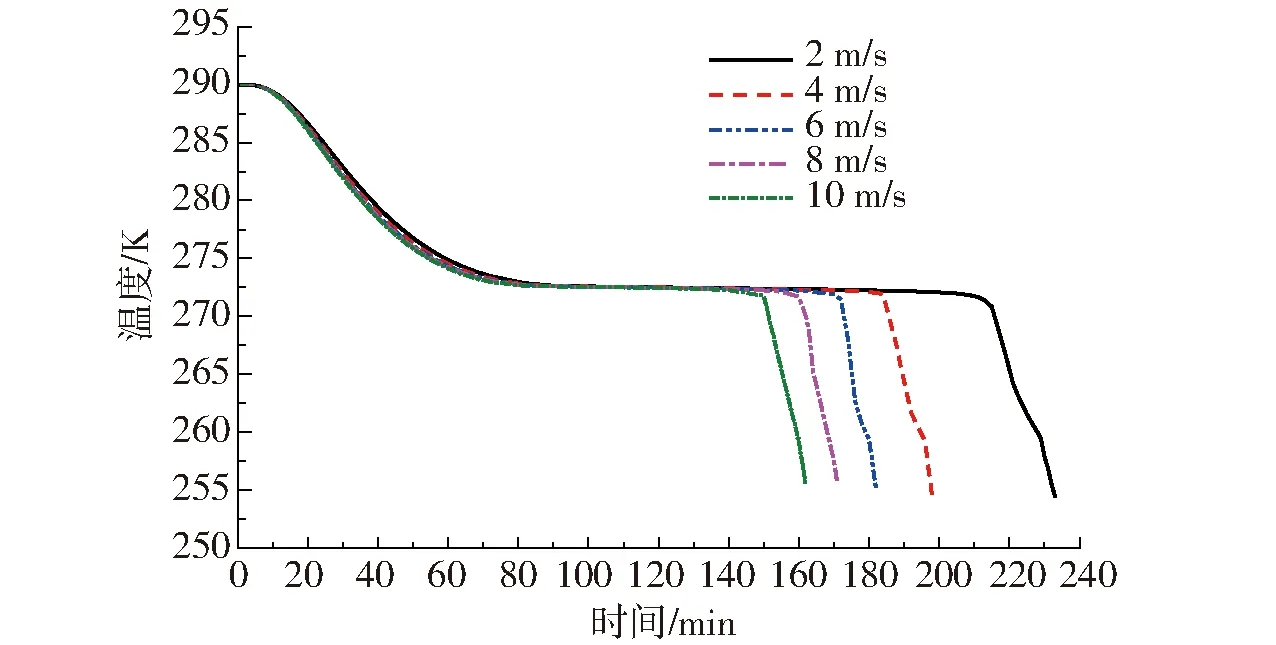
图7 风速对马铃薯泥中心降温过程的影响Fig.7 Effect of air velocity on freezing process
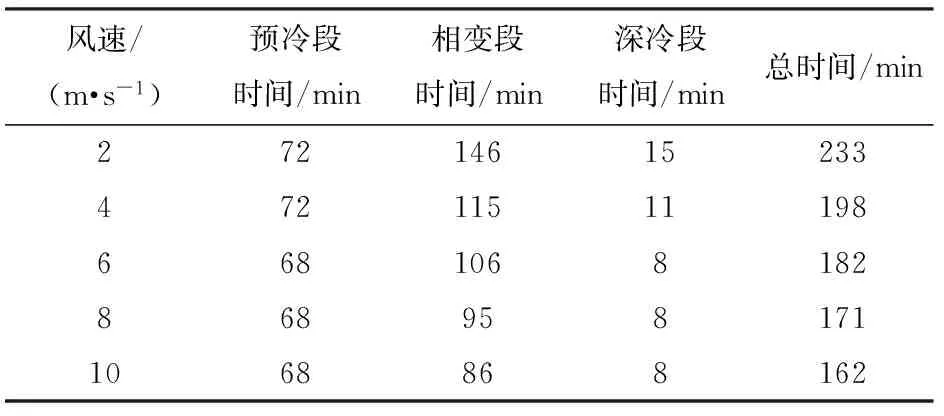
风速/(m·s-1)预冷段时间/min相变段时间/min深冷段时间/min总时间/min272146152334721151119866810681828689581711068868162
可以看出,在送风温度相同的情况下,风速对预冷段的影响很小,对相变段的影响最大,对深冷段的影响也较为明显。这与文献[18]的结论一致。随着风速的增加,整体冷冻时间呈现递减趋势,而缩短的时间中相变段减少的时间占比超过50%。冷冻时间的递减幅度随风速的增加逐渐放缓,考虑到风机能耗与频率是三次方的关系[19],在实际生产中可以根据能耗指标和冷冻时间合理选择不同冷冻阶段的风速。当预冷段、相变段、深冷段的风速分别为4、8、4 m/s时,模拟得到的冷冻时间为184 min,这与全过程风速为4 m/s的情况相比,时间缩短了27 min。
冷冻结束时,不同位置的马铃薯泥中心温度并不相等,利用温度变异系数[20]来评价不同位置马铃薯泥之间的温度差异性。计算式为
(5)
风速对马铃薯泥中心温度变异系数的影响如图8所示。马铃薯泥中心温度变异系数随着风速的增加呈现先减小后增大的变化趋势,风速为6 m/s时中心温度变异系数最小,即不同位置的马铃薯泥之间中心温度差异性最小。
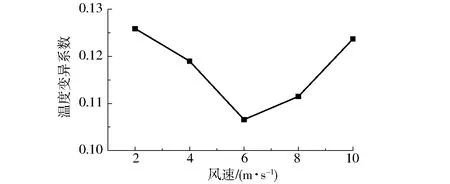
图8 风速对马铃薯泥中心温度差异性的影响Fig.8 Effect of air velocity on variation coefficient of temperature
除了不同位置马铃薯泥之间的温度差异性,还应该关注冷冻过程中风速对马铃薯泥内外温度均匀性的影响。不同风速下马铃薯泥几何中心点与沿Y轴方向距离中心40 mm点的平均温差变化曲线如图9所示。马铃薯泥在冷冻过程中,其内外温差会出现2次大的升降变化[21]。第1次升高是由于冷量在由外向内传播的过程中逐渐被吸收,降温速率由外向内递减,二者温差逐渐增大;当距离中心40 mm处的点进入相变段后,由于潜热的释放,其降温速率大大降低,而中心点依然处于预冷段,降温速率大于外侧相变点的降温速率,使得二者温差逐渐减小。当外侧点相变结束时,若中心点尚未进入相变段,则二者温差会出现一个小的波动,在风速大于6 m/s时该现象较为明显。这也说明,随着风速的增大,冷冻过程中马铃薯泥内外温度均匀性会降低。当中心点进入相变段后,其降温速率远小于已经处于深冷段的外侧点,二者温差逐渐增大到整个冷冻过程的最大值。中心点相变结束后,二者温差迅速减小。图9还表明,随风速的增大,冷冻过程中的最大温差也增大。
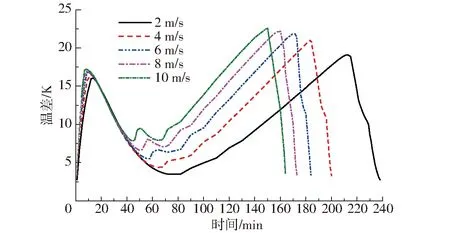
图9 风速对马铃薯泥内外温差的影响Fig.9 Effect of air velocity on temperature difference
4.2 送风温度对冷冻过程的影响
根据以上模拟结果,在风速为6 m/s的条件下,模拟马铃薯泥在不同送风温度下的冷冻过程。图10是在送风速度为6 m/s的条件下,送风温度对马铃薯泥冷冻时间的影响。冷冻过程中各个阶段的具体时间如表3所示。可以看出,随着送风温度降低,马铃薯泥冷冻时间逐渐缩短,而且相变段缩短的时间在缩短的总时间中比重最大。送风温度对预冷段的影响最小。当预冷段、相变段、深冷段的送风温度分别为248.15、238.15、248.15 K时,模拟得到的冷冻时间为175 min,这比全过程使用248.15 K节省了44 min。考虑到送风温度越低,制冷系统的制冷系数越小,因此,从节能方面考虑,结合不同冷冻阶段对温度的敏感程度,可以在预冷段采用较高的送风温度,等食品进入相变段后再降低送风温度,即满足了冷冻时间的要求,还可以降低能耗。
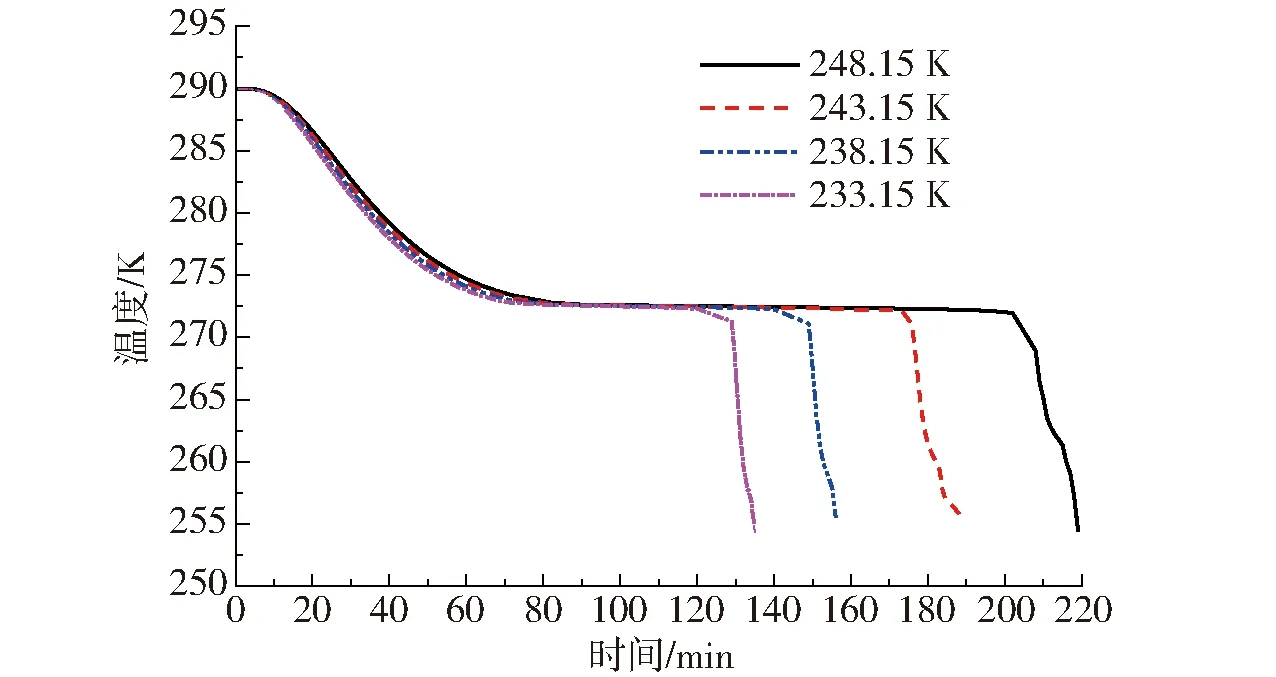
图10 温度对马铃薯泥中心降温过程的影响Fig.10 Effect of temperature on freezing time
冷冻结束后,送风温度对马铃薯泥中心温度变异系数的影响如图11所示。从图11可看出,随着送风温度的降低,马铃薯泥中心温度变异系数呈先上升而后略有下降的趋势。图12是送风温度对马铃薯泥内外温差的影响。随着送风温度的降低,内外温差均匀性下降,最大温差增大。
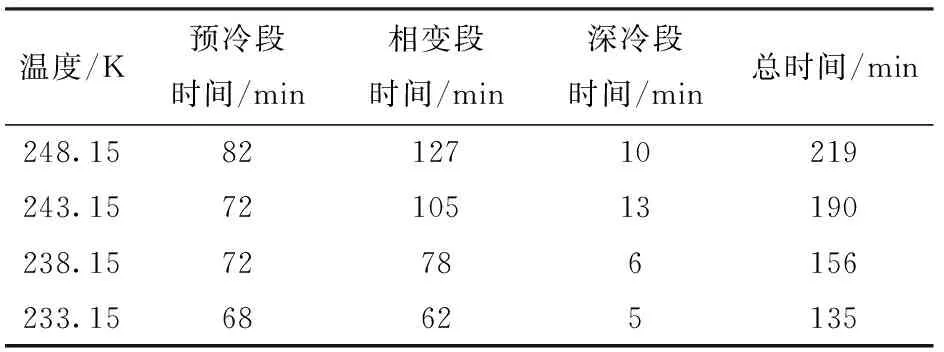
表3 不同温度条件下各阶段降温时间
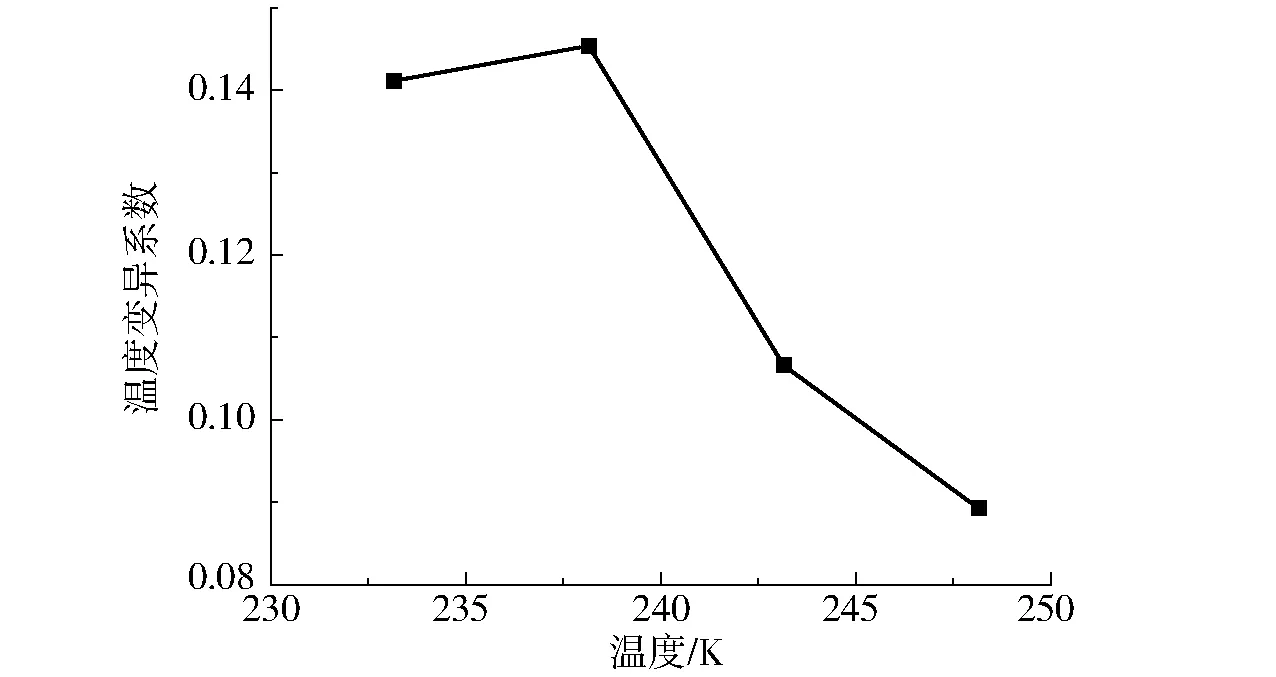
图11 温度对马铃薯泥中心温度差异性的影响Fig.11 Effect of air temperature on variation coefficient of temperature

图12 温度对马铃薯泥内外温差的影响Fig.12 Effect of air temperature on temperature difference
5 结论
以无包装短圆柱状马铃薯泥的冷冻过程为研究对象,采用数值模拟方法建立了马铃薯泥鼓风冷冻三维数值模型,通过改变送风速度和温度,分别研究两者对马铃薯泥冷冻过程的影响。结论如下:
(1)模拟结果与实验结果吻合较好。模拟结果和实验结果的温差最大值出现在深冷段,为7.1 K,冷冻时间相对误差为3.9%。
(2)冷冻时间随送风速度的增加而缩短,当风速超过6 m/s时,冷冻时间缩短的程度放缓。冷冻结束时马铃薯泥中心温度之间的差异性随着风速的增加呈现先减小后增大的趋势。随着风速的增大,冷冻过程中马铃薯泥内外温度均匀性会降低,最大温差增大。风速对相变段的影响比预冷段和深冷段大。
(3)降低送风温度可以缩短冷冻时间,但会提高马铃薯泥中心温度之间的差异性,降低马铃薯泥内外温度均匀性。送风温度对相变段的影响大于预冷段和深冷段。在实际冷冻过程中,可以在不同的冷冻阶段选用不同的送风速度和温度,做到缩短冷冻时间和降低能耗二者兼顾。
1 ZARITZKY N E. Factors affecting the stability of frozen foods[M]∥KENNEDY C J. Managing frozen foods. Cambridge:Wood-head Publishing Limited,2000:111-133.
2 朱迪斯 A E. 冷冻食品科学与技术[M]. 许学勤,译.北京:中国轻工业出版社,2009:4-8.
3 ZARITZKY N E. Physical-chemical principles in freezing[M]∥Handbook of frozen food processing and packaging. Boca Raton/London/New York: CRC Taylor/Francis Group, 2011:3-38.
4 CAMPANONE L A,SALVADORI V O,MASCHERONI R H. Food freezing with simultaneous surface dehydration: approximate prediction of freezing time[J]. International Journal of Heat and Mass Transfer,2005,48(6):1205-1213.
5 ERDOGDU F. Fundamental of heat transfer in food processing[M]∥Mathematical modeling of food processing. Boca Raton:CRC Press/Taylor and Francis Group,2010:69-88.
6 DELGADO A E,SUN D W. Heat and mass transfer models for predicting freezing processes—a review[J]. Journal of Food Engineering,2001,47(3):157-174.
7 PHAM Q T. Modeling heat and mass transfer in frozen foods: a review[J]. International Journal of Refrigeration,2006,29(6):876-888.
8 WIDELL K N. Energy efficiency of freezing tunnels:towards an optimal operation of compressors and air fans[D]. Trondheim:Norwegian University of Science and Technology,2012:37-38.
9 PHAM Q T. Freezing time formulas for foods with low moisture content, low freezing point and for cryogenic freezing[J]. Journal of Food Engineering,2014,127:85-92.
10 赵文峰,杨洲. 微型冷库货物降温特性的CFD数值模拟[J].中国科技论文,2015,10(5):546-551. ZHAO Wenfeng,YANG Zhou. Study on the temperature-dropping characteristics of products in the mini cooling store using CFD model[J]. China Science Paper,2015,10(5):546-551. (in Chinese)
11 李杰,谢晶. 鼓风冻结虾仁时间的数值模拟及实验验证[J]. 农业工程学报,2009,25(4):248-252. LI Jie,XIE Jing. Numerical simulation of freezing time of shelled shrimps in an air blast freezer and experimental verification[J]. Transactions of the CSAE,2009,25(4):248-252. (in Chinese)
12 杨世铭,陶文铨. 传热学[M]. 4版. 北京:高等教育出版社,2010:41-45.
13 DIMA J B,SANTOS M V,BARON P J,et al. Experimental study and numerical modeling of the freezing process of marine products[J]. Food and Bioproducts Processing,2014,92:54-66.
14 STEVEN D,ROCCA A L,POWER H,et al. Estimating the temperature evolution of foodstuffs during freezing with a 3D meshless numerical method[J]. Engineering Analysis with Boundary Elements,2015,53:46-55.
15 韩佳伟,赵春江,杨信廷, 等. 基于CFD数值模拟的冷藏车节能组合方式比较[J]. 农业工程学报,2013,29(19):55-62. HAN Jiawei,ZHAO Chunjiang,YANG Xinting,et al. Comparison of combination mode of energy conservation for refrigerated car based on CFD numerical simulation[J].Transactions of the CSAE,2013,29(19):55-62. (in Chinese)
16 HUAN Zhongjie,HE Shaoshu,MA Yitai. Numerical and analysis for quick-frozen food processing[J]. Journal of Food Engineering,2003,60:267-273.
17 王娟,谭金翠,王相友. 风速对双孢蘑菇预冷过程的影响[J/OL]. 农业机械学报,2013,44(10):203-208. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20131033&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2013.10.033. WANG Juan,TAN Jincui,WANG Xiangyou. Effect of air velocity on pre-cooling process ofAgaricusbisporus[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2013,44(10):203-208. (in Chinese)
18 洪乔荻. 馒头变温速冻过程的数值模拟与实验研究[D]. 天津:天津商业大学,2014:47-49. HONG Qiaodi. Numerical simulation and experiment on multi-temperature quick-frozen process of steamed bread[D]. Tianjin:Tianjin University of Commerce,2014:47-49. (in Chinese)
19 吕恩利,陆华忠,韩小腾, 等. 气调保鲜运输车变频通风系统调控与能耗分析[J]. 农业工程学报,2012,28(16):248-253. LÜ Enli,LU Huazhong,HAN Xiaoteng,et al. Regulation and energy consumption analysis on frequency conversion ventilation system of fresh-keeping truck with controlled atmosphere[J]. Transactions of the CSAE,2012,28(16):248-253. (in Chinese)
20 郭嘉明,吕恩利,陆华忠, 等. 盒装荔枝果实降温特性数值分析与验证[J/OL]. 农业机械学报,2016,47(5):218-224. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160530&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.05.030. GUO Jiaming,LÜ Enli,LU Huazhong,et el. Numerical simulation on temperature field effect of strack method of garden stuff for fresh-keeping transportation[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016,47(5):218-224. (in Chinese)
21 杨瑞丽. 土豆冻结过程中相变界面的模拟及实验研究[D]. 天津:天津商业大学,2014:29-31. YANG Ruili. Simulation and experimental study on phase change interface during the freezing process of potato[D]. Tianjin:Tianjin University of Commerce,2014:29-31. (in Chinese)
Numerical Analysis and Test on Characteristics of Temperature Decreasing of Mashed Potatoes
WAN Jinqing YUE Zhankai LI Jianguo WANG Youjun
(CollegeofFoodScienceandTechnology,ShanghaiOceanUniversity,Shanghai201306,China)
In order to investigate the characteristics of temperature decreasing of mashed potatoes without packages during freezing in an air blast freezer,a three-dimensional unsteady numerical model was established to simulate the freezing process of mashed potatoes. According to the thermo-physical properties of mashed potato, the process of the temperature decreasing during freezing was simulated by Fluent,after which the airflow information in the container was obtained.A test was done to verify the accuracy of the model,and it was found that the simulation values and test values were in good agreement,the maximum temperature difference between the test data and simulation result was 7.1 K and the relative error of freezing time was 3.9%. After that,two design parameters (air velocity and air temperature) which would affect the freezing process were analyzed.Improving the air velocity can shorten the time of freezing but would improve the maximum temperature difference between the mashed potato’s core and edge. The variation coefficient of temperature among mashed potatoes was firstly increased and then decreased with the increase of air velocity, and it was minimum when the air velocity was 6 m/s. When the air velocity was bigger than 6 m/s,the freezing rate trended to be steady along with the growing of air velocity. Reducing the air temperature can effectively improve the temperature decreasing of mashed potatoes during freezing but also would improve the variation coefficient of temperature among mashed potatoes. The results reviewed some characteristics of the freezing of mashed potatoes without packages in an air blast freezer, which can provide a reference value for the optimization of the equipments and technologies for the freezing of foodstuffs.
mashed potatoes; air blast; freezing time; characteristics of temperature decreasing; numerical simulation
10.6041/j.issn.1000-1298.2017.04.039
2016-12-29
2017-02-13
国家高技术研究发展计划(863计划)项目(2012AA092301)
万金庆(1964—),男,教授,博士,主要从事制冷系统节能技术与食品保鲜技术研究,E-mail: jqwan@shou.edu.cn
TB69; TS205.7
A
1000-1298(2017)04-0298-07

