潜在特质模型在疾病易感性评价中的应用*

刘 娜 石志红 曹红艳 郭兴萍 张岩波△

潜在特质模型在疾病易感性评价中的应用*

刘 娜1石志红1曹红艳1郭兴萍2△张岩波1△

目的 介绍潜在特质模型的原理、方法和技术，探讨潜在特质模型在疾病易感性评价中的应用。方法 以出生缺陷数据为实例，采用R 2.5.1软件的Ltm包例证潜在特质模型的构建和分析原理。结果 通过对出生缺陷数据进行潜在特质模型拟合，潜在特质得分能够很好地预测评估其发病危险。结论 潜在特质模型用于疾病患病风险评价有很好的效果。

潜在特质模型 疾病易感性评价 出生缺陷 潜在特质得分

潜变量模型(latent variable model)利用外在直接观察到的变量分析内在因素，通过分析外在变量与内在变量(潜变量)及内在变量之间的关系来探究事物的发生、发展、变化规律及特点[1]。潜在特质模型(latent trait model)属于潜在变量模型的一种，兼具因子分析与聚类分析的功能，具有数据降维、数据挖掘和理论验证的统计学功能，适用于显变量为分类型，潜变量为连续型的资料[2]。在医学研究中，对疾病易感性的评价涉及影响因素非常多，既有能够较为准确测量的因素，又存在许多无法直接测量的指标，同时，各指标间可能存在相关。对这些因素的研究，不仅要研究单个变量的效应，也要研究一组变量的整体效应。传统的患病风险评价，直接对暴露因素得分进行简单相加求和以考察疾病危险程度，并采用卡方检验和logistic回归进行分析，显然远不足以挖掘疾病的潜在暴露因素，无法综合地评价疾病的患病风险。因此，本文将介绍潜在特质模型在疾病患病风险评价中的应用，为易感性评价提供良好的分析策略。

方法与原理

1.模型结构

潜在特质模型包括两个部分：第一部分是测量模型，反映了显变量与潜变量之间的关系，可以解释各显变量之间的潜在结构；第二部分是结构模型，研究潜变量之间的结构关系。

(1)测量模型

假定条目yj是分类变量，它有Lj个可能分类水平：l=1,…,Lj，不同类型的条目，分类变量水平是不同的。对于等级资料的条目，其分类变量水平是等级的，顺序不能发生改变，除非采用反向记分；对于无序分类资料，其分类变量水平是随机的；而对于二分类资料，既可以看成是等级资料也可以看成是无序分类资料。yi的测量模型其实是一个分类概率回归模型：

πjl(η)=p(yj=l|η)

其中，η为解释变量。

(2)结构模型

潜在特质模型假定潜在变量η取某一固定值时，j维列联表x可通过其边际分布来解释，在此假设条件下，潜在因子分布pη为结构模型。一般情况下，假设潜在因子η服从均数为k，标准差为φ的正态分布，即η～N(k,φ)。在模型设定中，一般限定k=0，φ=1，否则需调整测量模型中的参数。

2.常见的潜在特质模型

潜在特质模型在心理测量领域被称为项目反应理论，它建立了组成测验的项目与测验分数之间的函数关系。到目前为止，潜在特质模型产生了至少20余种模型。可以根据不同的反应数据选择相应的模型来估计参数。

(1)Rasch模型

Rasch模型在1960年首次被Rasch提出，是一个单维潜在特质模型的特例，它的区分度是相同的，主要应用于教育测验，目的是研究特定个体的能力值，可以用潜在因子对量表内的项目进行评估[4]。模型被定义为：

其中，P(Yij=1)代表第i个个体对第j个条目正确回答的概率。θ表示能力值，β表示难度系数[5]。

(2)双参数logistic模型(Ltm模型)

对于显变量为二分类的数据，潜在特质模型与因子分析模型相似，是潜在特质模型的一种。模型假设有相互依赖关系的外显变量可以被少数的几个潜变量所解释。该模型的公式是项目反应理论框架下的一种方法。

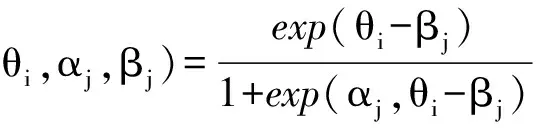
其中，α代表区分度系数。

3.参数估计方法

潜在特质模型的参数估计一般采用极大似然法(maximumlikelihoodestimators)[3]，其迭代过程常用的算法有EM算法和拟牛顿法(quasi-Newton)。本文参数估计选用混合算法进行计算，即开始时使用EM算法进行迭代，然后用拟牛顿算法迭代直至收敛。

4.模型评价

潜在特质模型常用的评价方法有似然比检验、Pearson检验及AIC(akaikeinformationcriterion)指标和BIC(bayesianinformationcriterion)指标。AIC和BIC的值越小，模型拟合越好[6-8]。本文综合使用AIC、BIC及似然比检验进行模型拟合优劣比较。同时，采用双变量边际残差进一步地判断模型拟合是否良好。

5.潜在特质得分与主成分得分

最优模型确定后，将观察值代入模型中，获得个体潜在特质的预测值，即给出各条目综合得分。其条件均数为：

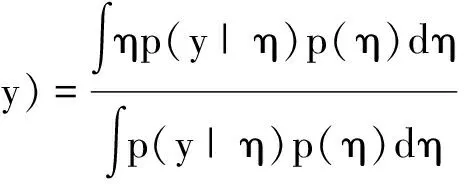
同时，计算出外显变量对公共因子贡献的权重αi1，即得出该模型的主成分得分：

C1(y)=∑αi1yi

潜在特质得分与主成分得分对不同条目进行了聚类，挖掘了其隐含的内在信息，综合反映了各条目之间的整体效应，实现了降维的目的，可以作为衡量疾病易感性的重要指标，得分越高，患病的危险性越大。

实例分析

为实证潜在特质模型应用原理，本文利用2006-2008年在山西省6个出生缺陷高发县(市)收集的有效问卷36712份进行潜在特质模型分析。问卷内容包括七个方面：调查儿母亲一般情况、母亲既往病史、妊娠早期营养状况、妊娠早期患病、妊娠早期服药、妊娠早期周边环境、妊娠早期生活习惯，共计25个条目。将所有条目转化为二分类变量，如母亲年龄大于等于35岁的为1，小于35岁的为0。本文仅对调查儿母亲一般情况和妊娠早期患病这两个维度进行潜在特质分析。采用R 2.5.1软件的Ltm包进行分析。

结 果

对调查儿母亲一般情况和妊娠早期患病这两个维度进行模型拟合，得到参数估计结果，结合AIC、BIC和似然比检验对Ltm模型与Rasch模型进行拟合优度评价，选出最优模型。此外还可用双变量边际残差的方法对模型进行评估。最后通过计算潜在特质得分及主成分得分，对出生缺陷患病风险进行评价。

1.参数估计结果

本文采用最大似然估计算法得到双参数的值，其中α代表区分度系数，β代表难度系数。由表1可知各条目的区分度系数为0.2819～7.6206，总的来讲能很好的反映不同受试者的能力。β值在1.6486～7.8763，本文中我们暂不对其难度系数进行考虑。具体参数估计结果见表1。

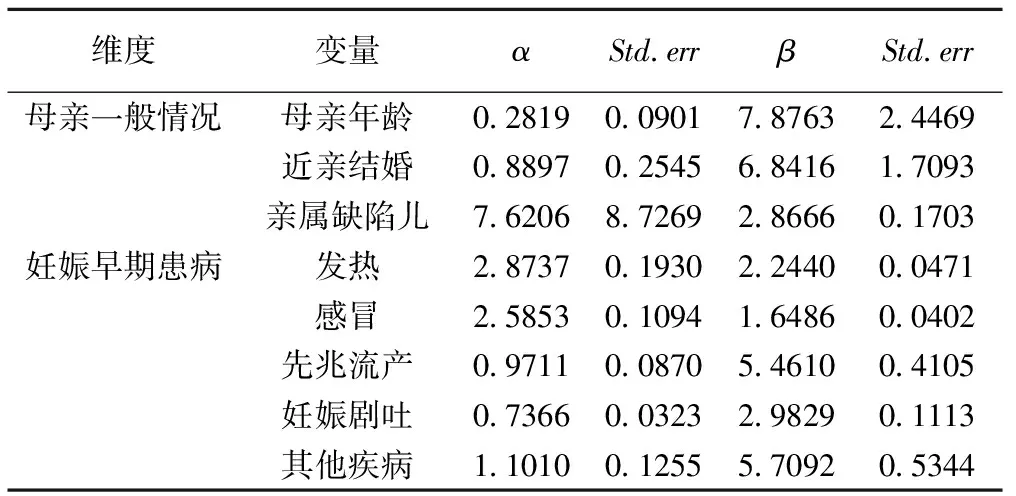
表1 出生缺陷母亲一般情况及妊娠早期患病参数估计结果

2.模型适配结果及拟合优度评价

对出生缺陷数据进行Ltm与Rasch模型拟合，其中，母亲一般情况及妊娠早期患病两个维度拟合Ltm与Rasch模型结果见表2。

由表2可知，Ltm模型的AIC和BIC值比Rasch模型所得值小，AIC和BIC值越小，模型拟合越好。似然比检验显示，两个模型检验都有统计学意义。Ltm模型比Rasch模型能更好的拟合出生缺陷数据。同时双变量边际残差结果也显示模型拟合效果良好。

表2 母亲一般情况及妊娠早期患病Ltm与Rasch模型拟合结果

3.潜在特质得分与主成分得分

将出生缺陷相关暴露因素放入Ltm模型进行拟合，可以得到多个反应模式。为了便于比较，将每个暴露因素为“是”的赋值为1，为“否”的赋值为0，直接相加求和得分，定义为“表面得分”。母亲一般情况和妊娠早期患病两个维度的表面得分与潜在特质得分结果见表3。

表3中，不同反应模式下，潜在特质得分为-0.029～3.009，即随着暴露因素的增多，潜在特质得分增大，出生缺陷发生的危险性变大。另一方面，通过对不同反应模式的比较，如(0 0 1)和(0 1 0)可知各主成分得分是不一样的。显然，在母亲一般情况维度，亲属有缺陷儿的孕母发生出生缺陷的风险更大。同理，表4结果提示单因子暴露下，发热与感冒发生出生缺陷的风险较大，不同暴露组合发病风险可由潜在特质得分评价。

进一步将出生缺陷组的潜在特质得分与非出生缺陷组的潜在特质得分做t检验，所得结果见表5。

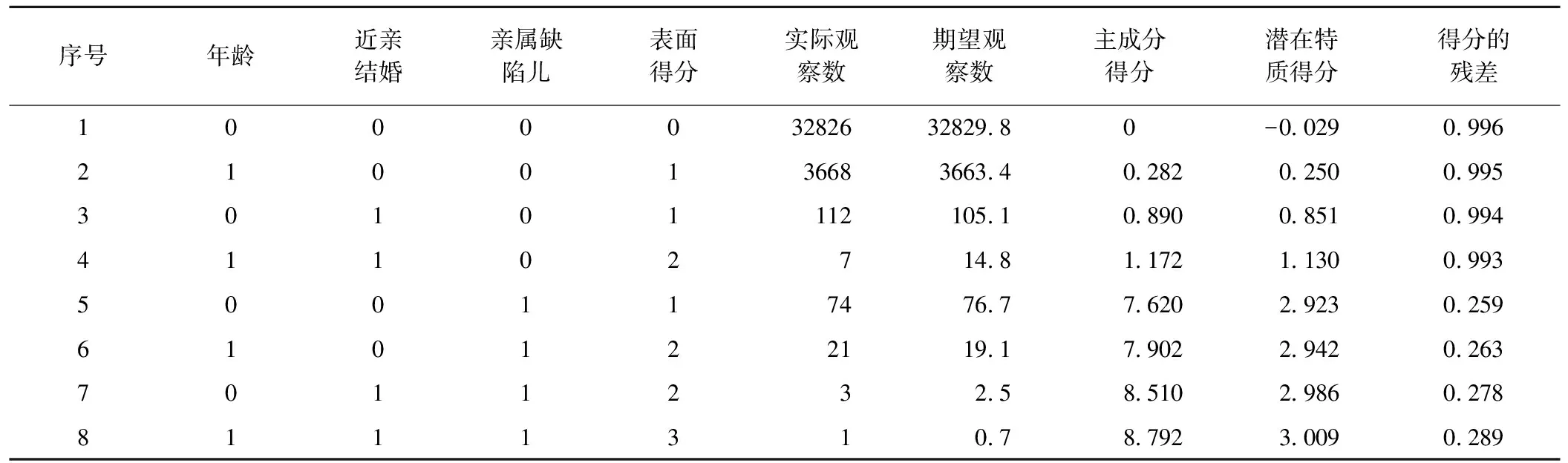
表3 母亲一般情况潜在特质得分

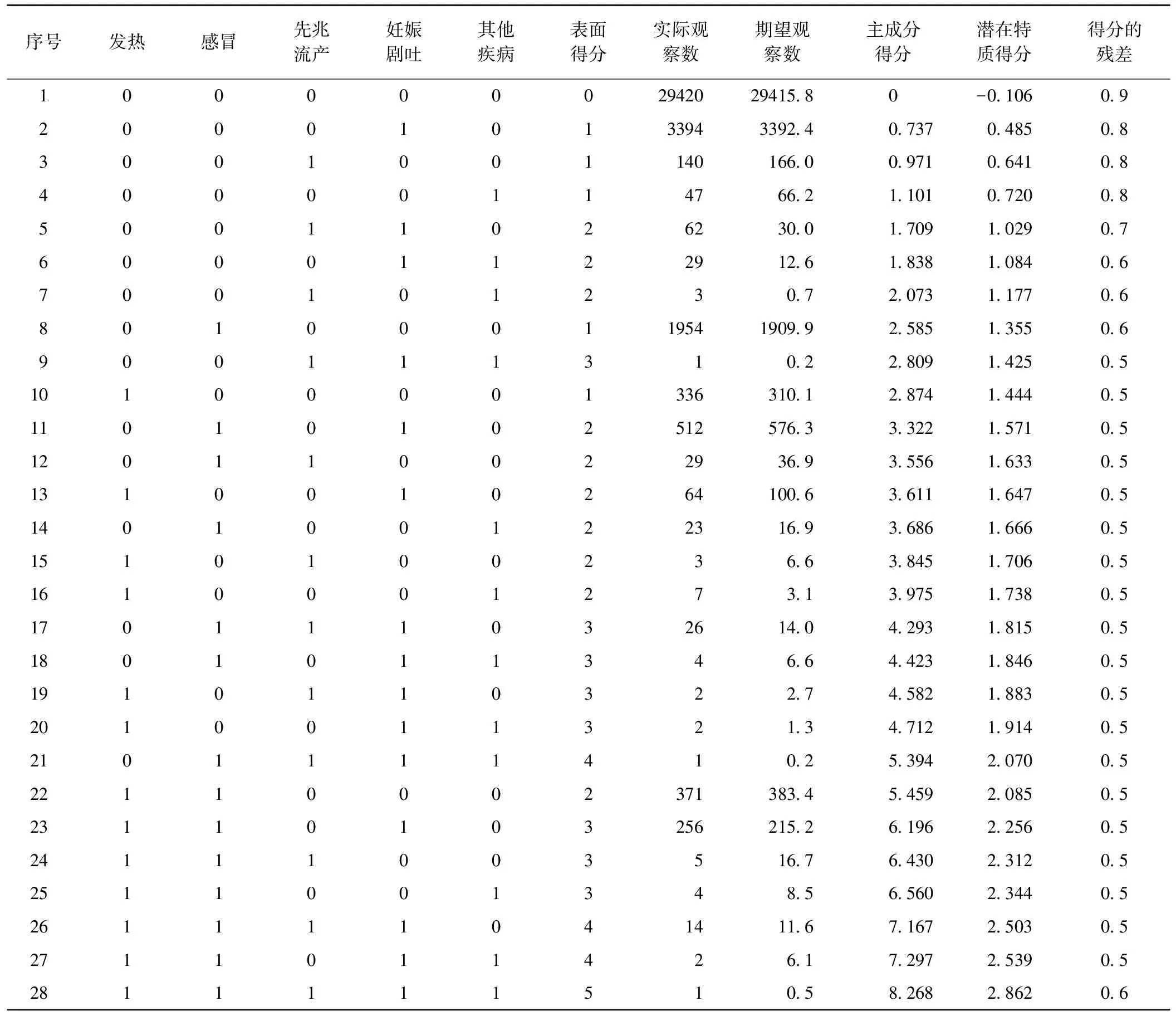
表4 妊娠早期患病情况潜在特质得分

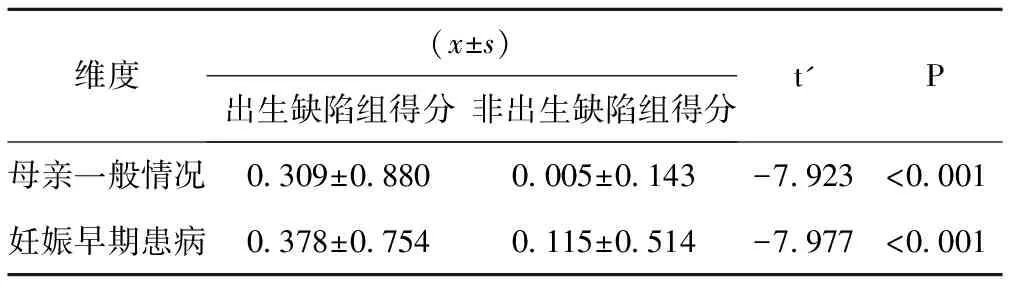
表5 出生缺陷组和非出生缺陷组在母亲一般情况与妊娠早期患病两个维度中的潜在特质得分比较

由表5可知，两个维度出生缺陷组和非出生缺陷组的潜在特质得分差异有统计学意义，认为出生缺陷组的潜在特质得分明显高于非出生缺陷组。

讨 论

潜在特质模型是潜变量分析的一种，是探讨外显变量为分类变量，潜变量为连续变量的一种最佳统计方法。通过潜在特质变量解释多个外显变量间的复杂关系，并将其外显变量综合为一个潜变量，使之能够代替外显变量分析整体效应。通过所得到的潜在特质得分的大小可以对疾病患病风险进行评价。实例分析中的外显变量为二分类变量，但在实际应用中潜在特质模型还可应用于多分类的名义变量、有序变量等[9]。

目前，潜在特质模型分析的软件很多，如R、Mplus、Multilog等。本文运用R软件中的Ltm包进行分析，相对于其他软件，不仅能够得到潜在特质得分，而且具有语法结构简单，易于掌握的特点和优势。

本文分析母亲一般情况和妊娠早期患病两个维度，采用的是双参数logistic模型(Ltm模型)。不同反应模式下，潜在特质得分不同。暴露因素越少，得分越低，反之，得分越高。同时根据不同反应模式的主成分得分不同，对各维度暴露因素权重进行了比较。可进一步探索多因子潜在特质模型，将暴露因素综合为几个潜在因子，并对其关联性进行分析；也可采用多样本潜在特质模型，对不同样本的暴露因素进行比较，进一步挖掘出疾病暴露因素，提高疾病预测精度。

[1]张岩波.潜变量分析.北京:高等教育出版社,2009:220-246.

[2]Moustaki I,Knott M.Generalized latent trait models.Psychometrika,2000,65(3):391-411.

[3]David J.Latent Variable Models and Factor Analysis:A Unified Approach,3rd;Edition.International Statistical Review,2013,81(2):333-334.

[4]晏子.心理科学领域内的客观测量—Rasch 模型之特点及发展趋势.心理科学进展,2010,18(08):1298-1305.

[5]Yu-Feng Huang,Mei-Yung Tsou,En-Tzu Chen,et al.Item response analysis on an examination in anesthesiology for medical students in Taiwan:A comparison of one-and two-parameter logistic models.Journal of the Chinese Medical Association,2013,76(6):344-349.

[6]Gollini I,Murphy TB.Mixture of latent trait analyzers for model-based clustering of categorical data.Statistic & Computing,2013,24(4):569-588.

[7]Choi I.Model Selection for Factor Analysis:Some New Criteria and Performance Comparisons.Working Papers,2013.

[8]Hirose K,Kawano S,Konishi S,et al.Bayesian Information Criterion and Selection of the Number of Factors in Factor Analysis Models.Journal of Data Science,2011,9.

[9]David Kaplan.The Sage Handbook of Quantitative Methodology for the Social Sciences.Applied Psychological Measurement,2006,30(5):447-451.

(责任编辑：刘 壮)

国家自然科学基金(71403156)

1.山西医科大学公共卫生学院卫生统计学教研室(030001)

2.山西省计生委科研所

△通信作者：张岩波，E-mail：sxmuzyb@126.com;郭兴萍，E-mail：13934527993@163.com