MIMU/GNSS紧组合精密单点定位协方差成形自适应滤波方法

刘 斌，穆荣军，马新普，蒋金龙，崔乃刚

（1. 哈尔滨工业大学 航天学院，哈尔滨 150001；2. 航天科工集团第四研究院 第九总体设计部，武汉 100191）

MIMU/GNSS紧组合精密单点定位协方差成形自适应滤波方法

刘 斌1，穆荣军1，马新普2，蒋金龙2，崔乃刚1

（1. 哈尔滨工业大学 航天学院，哈尔滨 150001；2. 航天科工集团第四研究院 第九总体设计部，武汉 100191）

针对精密单点定位应用需求，研究了MIMU/GNSS紧组合协方差成形自适应滤波方法。给出了“位臵滤波器+速度滤波器”的分布式滤波器设计方案以降低计算复杂度；推导了地理系紧组合导航系统模型，并把伪距测量不一致性偏差扩展至系统状态向量中予以估计，从而提高系统对于动态环境下伪距测量偏差抖动的适应能力。协方差成形自适应滤波算法利用 Frobenius范数来衡量系统残差噪声水平建模状态与实际状态的匹配程度，并以最小化 Frobenius范数作为优化指标，动态调节滤波增益，以此来提高状态估计精度、平稳性与鲁棒性。地面静态试验表明：紧组合协方差成形自适应滤波器定位误差均值与均值稳定性均优于标准卡尔曼滤波器，定位精度提高了约50%，能够提供亚米级单点定位导航服务。相较于集中式滤波器设计方案，分布式滤波器方案计算复杂度降低了63.5%。

紧组合；惯性导航；卫星导航；协方差成形；精密单点定位；自适应滤波

SINS/GNSS紧组合导航方法已经被广泛研究并应用于车辆与飞行器系统中。在现有的研究工作中，松散组合与紧组合导航系统能够在无遮挡条件下提供相同精度的导航定位服务[1]，且对于松散组合系统而言，卫星接收机内部采用最小二乘迭代器或卡尔曼滤波器进行导航解算，通常情况下系统收敛性与动态性能均优于紧组合导航系统[2-3]。但在复杂应用环境下，例如，卫星可见性较差、受外界干扰导致接收机性噪比减弱以及卫星星座频繁切换时，采用紧组合系统具有一定优势[4-5]。

无人驾驶飞行器（Unmanned Aerial Vehicle，UAV）在很多应用场合需要高精度单点定位服务，且UAV工作环境一般较为复杂[6-8]。大的姿态机动导致卫星接收机可见卫星星座的频繁切换，以及复杂应用环境下卫星星座的遮挡和多路径效应的影响，导致采用松散组合方式一般无法满足系统精度与数据平稳性要求[9-11]。采用紧密组合方式，并对传统紧组合导航系统模型与滤波方法进行改进，以提高系统对于复杂环境的适应性，将可能成为解决UAV精密单点定位问题的一种有效解决途径。

本文主要对改进的SINS/GNSS紧组合导航方法进行研究，在系统模型中引入伪距偏差不一致性作为待估计状态向量，通过合理设计滤波器参数以补偿不同仰角卫星伪距测量偏差不一致性与伪距偏差抖动对于滤波平稳性与精度的影响。与此同时，为提高系统对于外界干扰的抑制能力，增强系统鲁棒性与快速收敛性，在传统卡尔曼滤波方法基础上，增加协方差成形环节，综合实测与预测信息，把协方差分为固定与可变两部分，通过比对系统残差建模状态与实测状态的匹配程度，以最小化协方差Frobenius范数[12]为优化指标，完成可变协方差部分自适应增益因子计算，实现对滤波器的自适应调节，以此来保证滤波估计精度与平稳性。

采用低成本微机械惯性测量单元（Miniature Inertial Measurement Unit, MIMU）与低成本多频卫星接收机组建地面实验系统，开展紧组合导航单点定位地面静态试验，对紧组合导航方法进行性能分析与精度评估验证。

1 改进的紧组合导航系统模型

传统紧组合系统模型建立在WGS-84坐标系下[13-14]，而常用惯性导航系统模型建立在地理坐标系下[15]，且对于地面应用来说，地理系模型更加有利于分析系统可观测性以及直观评价系统性能。为方便工程应用，在传统模型基础上，推导给出地理系下紧组合导航系统模型。

不同仰角导航卫星信号的信噪比差异，以及多路径等影响，导致接收机伪距测量偏差的一致性较差，从而极大地降低了系统定位精度。为解决该问题，引入伪距一致性偏差作为状态向量的增广予以估计，以此来提高系统对于观测信息扰动的适应能力，增强系统精度与鲁棒性。

1.1 改进的紧组合导航系统结构

采用“位置滤波器单元+速度滤波器单元”的分散式系统结构，以解决传统集中式滤波器高维矩阵计算量过大的问题。利用速度反馈修正以阻尼惯性导航系统位置积分偏差的发散，保持系统状态模型精度，分散式紧组合系统结构见图1。

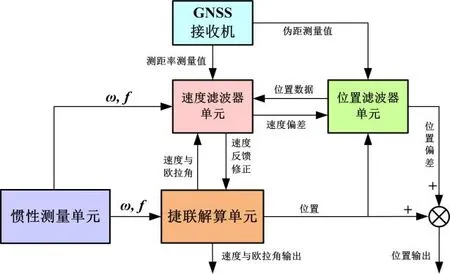
图1 SINS/GNSS紧组合导航系统结构Fig.1 Structure of SINS/GNSS tightly-coupled inertial navigation system

1.2 位置通道紧组合系统模型

状态模型以惯性导航误差传播模型为基础，引入卫星伪距偏差不一致性作为扩展的状态向量以提高系统稳定性与精度；观测模型以卫星导航伪距模型泰勒级数展开得到。

1.2.1 状态模型

状态向量xp选取为

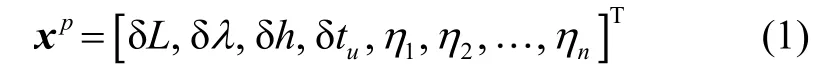
离散化后的状态方程为

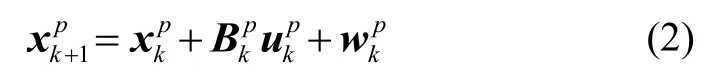
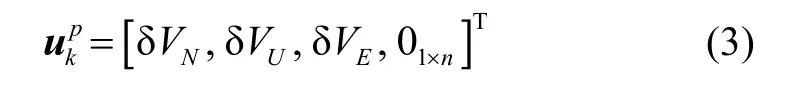
1.2.2 观测模型

地心地固坐标系紧组合系统伪距观测模型为：

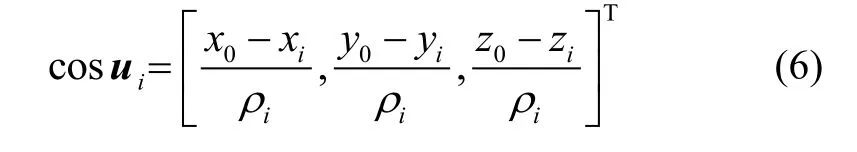
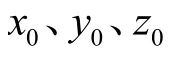
地理系与地心地固系位置转换关系为：

忽略纬度变化对卯酉圈半径RN的影响，对式(7)在(,,)

Lλh处进行泰勒级数展开，有：

写为矩阵形式有：

联合式(5)与式(10)，并且考虑每颗导航卫星测量伪距偏差的不一致性偏差，得到地理系下观测方程为

1.3 速度通道紧组合系统模型

状态模型根据惯性导航误差传播特性得到，观测模型利用伪距率模型泰勒级数展开得到。

1.3.1 状态模型

状态向量xv选取为

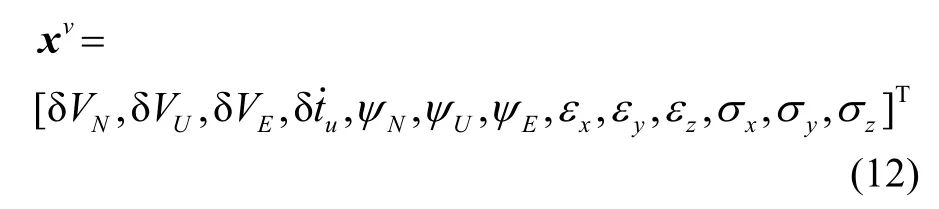
离散化后的状态方程为

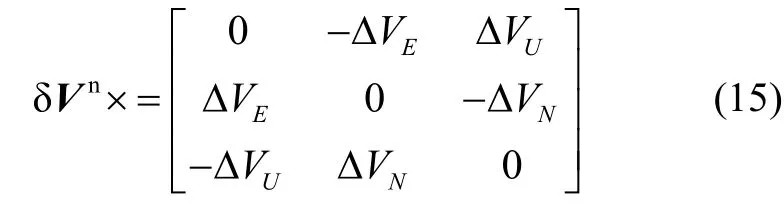
1.3.2 观测模型

地心系紧组合系统伪距率观测模型为

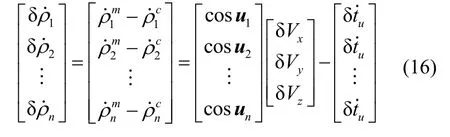
地理系速度偏差可通过坐标变换矩阵直接转换至地心系，即：

把式(17)代入式(16)中，得到地理系下伪距率对速度偏差的观测方程为

2 协方差成形自适应卡尔曼滤波方法

惯性导航系统误差传播模型可以采用如下线性系统进行表示：

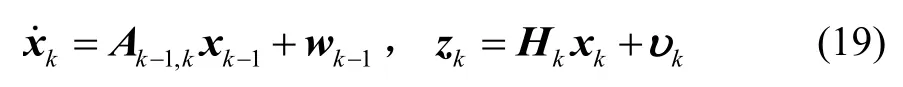
系统残差ek为

则系统测量残差方差Sk-1,k为

其中，Rk为测量噪声方差。

把状态预测协方差矩阵Pk-1,k写成如下形式：

其中，α为自适应增益因子。

把式(22)代入式(21)中，有：

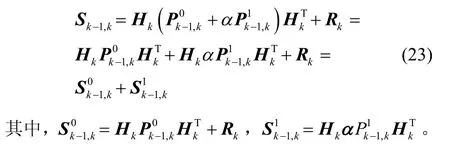
由式(22)可知，可以改变自适应增益因子α，实现对滤波器的自适应调节。系统实际残差方差的均值可以通过N点采样得到，即：

式(23)是卡尔曼滤波估计的残差协方差矩阵，式(24)是实测计算得到的残差协方差矩阵。以α为优化变量，可以得到使得式(23)与式(24)间偏差最小的代价函数，代价函数采用Frobenius范数表示，定义为

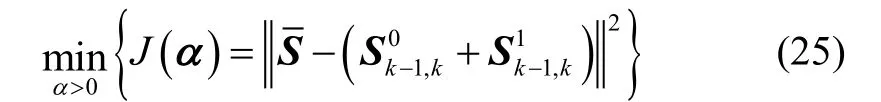
把式(22)与式(23)代入式(25)中，有：

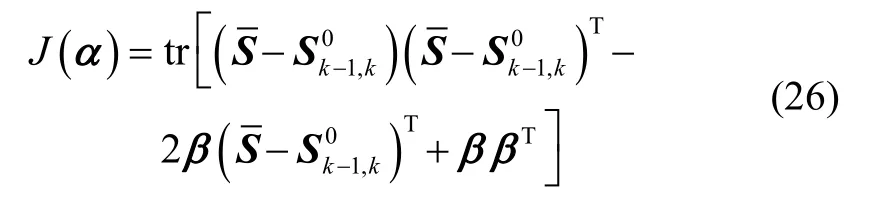
其中，

式(26)对α进行微分，考虑到β为反对称矩阵，有：

使得代价函数J(α) 最小，则有：

由于自适应增益矩阵α为对角矩阵，联合式(27)与式(29)，得到自适应增益矩阵α的计算公式为：

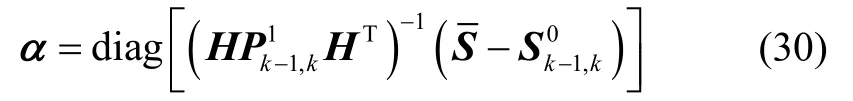
其中，diag[·]表示取对角线元素。

3 地面静态试验与分析

地面静态试验系统主要由微机械惯性测量单元、卫星导航接收机、数据采集计算机、数据融合处理计算机构成，系统结构、传感器指标以及硬件系统实物图如图2所示。

开展地面静态搜星试验以考核卫星接收机的伪距测量精度与稳定度，伪距测量偏差及与卫星仰角间的关系见图3。

由图3给出的静态搜星结果可以看出，高仰角卫星的测量伪距精度（6 m）明显优于低仰角卫星（10 m），且高低仰角卫星测量伪距的误差特性不一致。若采用标准卡尔曼滤波方法进行组合导航计算，伪距偏差的不一致性会影响导航定位精度（不满足高斯白噪声特性）。单次紧组合单点定位试验结果见图4。

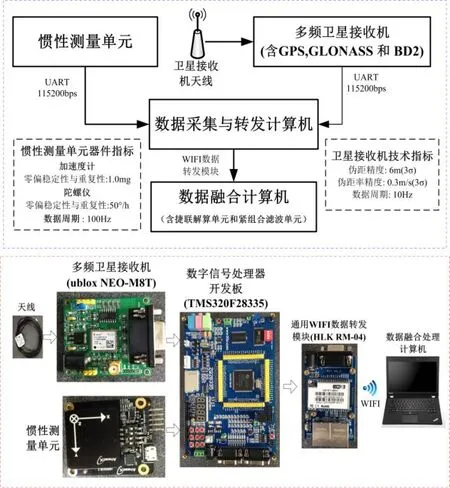
图2 地面静态试验系统结构与硬件实物图Fig.2 Structure and hardware of ground static test system

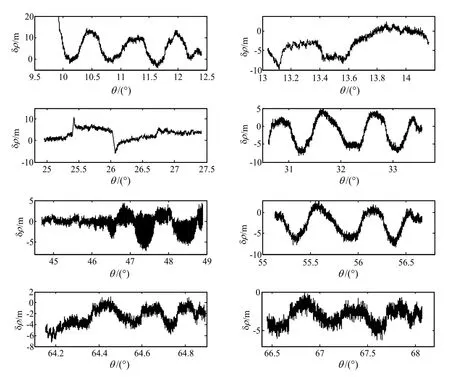
图3 卫星仰角-伪距偏差曲线Fig.3 Elevation angle vs. pseudorange deviation of satellite

由图4给出的单次试验数据可知，在定位数据平稳性与精度上，协方差成形自适应滤波器均优于标准卡尔曼滤波器，表明协方差成形自适应滤波算法具有更好的抗干扰能力。重复开展99次试验，得到紧组合精度统计结果见图5和图6。

图5和图6的精度统计结果表明：协方差成形自适应滤波器的定位均值精度与偏置稳定性均优于标准卡尔曼滤波器，定位精度提高了约50%。在无差分辅助的静态情况下，紧组合协方差成形自适应滤波器能够提供亚米级（水平1σ：0.65 m；高程1σ：0.82 m）的导航定位服务，能够有效解决UAV的高精度单点定位问题。

集中式与分布式紧组合滤波器的计算复杂度分析见表1。由表1可知，采用分布式滤波器结构较集中式滤波器结构，计算复杂度降低了63.5%。

表1 滤波器每万步计算耗时(实测)Tab.1 Time consuming per 104steps of filtering calculation

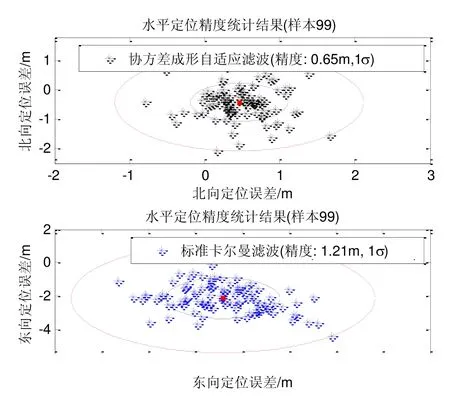
图5 水平定位精度统计结果Fig.5 Statistical results of horizontal positioning accuracy

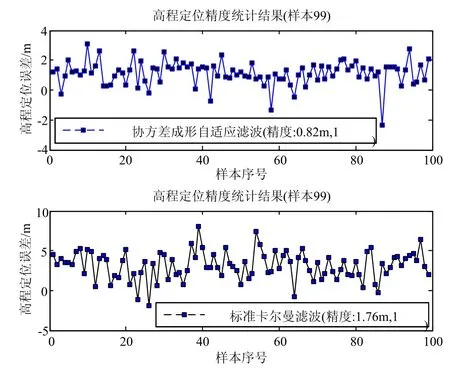
图6 高程定位精度统计结果Fig.6 Statistical results of vertical positioning accuracy

4 结 论

本文针对MIMU/GNSS紧组合精密单点定位自适应滤波方法开展研究，取得了以下三个较为典型的研究成果：

1）针对工程应用中对计算实时性要求，给出了“位置滤波器+速度滤波器”的分布式滤波器结构设计方案，与传统的集中式滤波器方案相比，计算实时性提高了63.5%。

2）推导给出了地理系下紧组合导航系统模型，与传统的WGS-84系模型相比，更加有利于分析系统可观测性等性能；把不同仰角卫星伪距测量偏差不一致程度扩展至状态向量中予以估计，提高了系统对于测量伪距偏差抖动的适应能力，进而有效保证状态估计的平稳性。

3）在标准卡尔曼滤波方法基础上，把状态预测协方差矩阵划分为固定部分与可变部分，通过对比残差协方差建模状态与实测状态的匹配程度，以最小化Frobenius范数为优化代价函数，动态计算状态预测协方差的自适应增益矩阵，实现对滤波器的自适应调节，提高滤波器对于测量抖动以及外界干扰的抑制能力，保证滤波估计的平稳性，提高滤波估计精度。地面静态试验表明：采用协方差成形自适应滤波方法能够提高定位精度约50%，在静态条件下能够获取亚米级定位精度。

（References）：

[1] Rabbou M A, El-Rabbany A. Tightly coupled integration of GPS precise point positioning and MEMS-based inertial systems[J]. GPS Solutions, 2015, 19(4): 601-609.

[2] Montillet J P, Yu K. Modified leaky LMS algorithms applied to satellite positioning[C]//2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall). 2014: 1-5.

[3] Nguyen T T T, Ta T H, Nguyen H L T, et al. An adaptive bandwidth notch filter for GNSS narrowband interference mitigation[J]. REV Journal on Electronics and Communications, 2015, 4(3-4): 59-68.

[4] Chiang K W, Lin C A, Peng K Y. The performance analysis of an AKF based tightly-coupled INS/GNSS sensor fusion scheme with non-holonomic constraints for land vehicular applications[C]//Applied Mechanics and Materials. Trans Tech Publications, 2013, 284: 1956-1960.

[5] 杨涛, 赵子阳, 李醒飞, 等. 多星座 GNSS/INS紧耦合方法[J]. 中国惯性技术学报, 2015, 23(1): 38-42. Yang Tao, Zhao Zi-yang, Li Xing-fei, et al. Tightly-cou pled integration method for multi-constellation GNSS/INS[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 38-42.

[6] Jiang F, Swindlehurst A L. Dynamic UAV relay positioning for the ground-to-air uplink[C]//2010 IEEE Globecom Workshops. 2010: 1766-1770.

[7] Caliskan F, Hacizade C. Sensor and actuator FDI applied to an UAV dynamic model[J]. IFAC Proceedings Volumes, 2014, 47(3): 12220-12225.

[8] Rahimi A M, Ruschel R, Manjunath B S. UAV Sensor fusion with latent-dynamic conditional random fields in coronal plane estimation[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016: 4527-4534.

[9] Falco G, Einicke G A, Malos J T, et al. Performance analysis of constrained loosely coupled GPS/INS integration solutions[J]. Sensors, 2012, 12(11): 15983-16007. [10] Nguyen V H. Loosely coupled GPS/INS integration with Kalman filtering for land vehicle applications[C]//2012 International Conference on Control, Automation and Information Sciences. 2012: 90-95.

[11] Hirokawa R, Ebinuma T. A low-cost tightly coupled GPS/INS for small UAVs augmented with multiple GPS antennas[J]. Navigation, 2009, 56(1): 35-44.

[12] Custódio A L, Rocha H, Vicente L N. Incorporating minimum Frobenius norm models in direct search[J]. Computational Optimization and Applications, 2010, 46(2): 265-278.

[13] 李增科, 高井祥, 姚一飞, 等. GPS/INS紧耦合导航中多路径效应改正算法及应用[J]. 中国惯性技术学报, 2014, 22(6) : 782-787. Li Zeng-ke, Gao Jing-xiang, Yao Yi-fei, et al. GPS/INS tightly-coupled navigation with multipath correction algorithm[J]. Journal of Chinese Inertial Technology, 2014, 22(6) : 782-787.

[14] 王琰, 张传定, 胡小工, 等. 卫星分群的抗差 Kalman滤波在GPS/BDS融合精密单点定位中的应用[J]. 中国惯性技术学报, 2016, 24(6): 769-774. Wang Yan, Zhang Chuan-ding, Hu Xiao-gong, et al. Robust Kalman filtering based on different satellite types and it's application in GPS/BDS precise point positioning [J]. Journal of Chinese Inertial Technology, 2016, 24(6): 769-774.

[15] 郑辛, 付梦印. SINS/GPS紧耦合组合导航[J]. 中国惯性技术学报, 2011, 19(1): 33-37. Zheng Xin, Fu Meng-yin. SINS GPS tightly-coupled integrated navigation[J]. Journal of Chinese Inertial Technology, 2011, 19(1): 33-37.

Covariance shaping adaptive filter method for tightly-coupled GNSS precise single-point positioning inertial navigation

LIU Bin1, MU Rong-jun1, MA Xin-pu2, JIANG Jin-long2, CUI Nai-gang1
(1. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China;
2. China Aerospace Science and Industry Corporation, Wuhan 100191, China)

According to the application requirement of the precision single-point positioning, the adaptive filtering method for MIMU/GNSS tightly-coupled system based on covariance shaping is studied. The distributed filter design of the “position filter + speed filter” is given to reduce the computational complexity. The model of MIMU/GNSS tightly-coupled system in geography system is deduced, and the pseudo-range measurement inconsistency is extended into the system state vector to improve the system’s ability to suppress the pseudo-range deviation jitter in dynamic environments. The covariance shaping adaptive filtering algorithm utilizes the Frobenius norm to measure the matching degree between the modeling and actuality of residual noise, and dynamically adjust the filter gain to minimize the Frobenius norm which is taken as the optimization index, in order to improve the state estimation accuracy, stability and robustness. The ground static test shows that the positioning error’s mean values and the mean-value’s stability of the covariance shaping adaptive filter are both better than those of the standard Kalman filter, and the positioning accuracy is increased by approximately 50%, and the sub-level single-point positioning navigation services can be provided. Compared with the centralized filter design scheme, the computational complexity of the distributed filter scheme is reduced by 63.5%.

tight combination; inertial navigation; satellite navigation; covariance shaping; precise point positioning; adaptive filtering

V249. 322；U666. 11

A

1005-6734(2017)02-0221-06

10.13695/j.cnki.12-1222/o3.2017.02.015

2017-01-04；

2017-03-28

国家高技术研究发展计划（863计划）（2015AA7026083）

刘斌（1989—），男，博士研究生，主要从事惯性导航初始对准、组合导航研究。E-mail: xiaobin_hit@163.com

联 系 人：崔乃刚（1965—），男，教授，博士生导师。E-mail: Cui_Naigang@163.com