晃动基座行进间对准问题的QUEST算法

郭玉胜，付梦印，邓志红，庄广琛，邓 亮

（1. 北京理工大学自动化学院，北京 100081；2. 北京自动化控制设备研究所，北京 100074 ）

晃动基座行进间对准问题的QUEST算法

郭玉胜1,2，付梦印1，邓志红1，庄广琛2，邓 亮2

（1. 北京理工大学自动化学院，北京 100081；2. 北京自动化控制设备研究所，北京 100074 ）

针对惯导系统晃动基座行进间初始对准问题，提出了一种基于重力矢量的QUEST（Quaternion Estimator）姿态最优估计算法。在传统基于重力矢量的初始对准方法基础上，将方向余弦矩阵的求解过程转换为Wahba问题，实现对重力矢量信息的充分利用，并通过QUEST算法实现了晃动基座下行进间粗对准的最优算法，改善了原有算法鲁棒性以及实时性等方面的问题。仿真和湖试实验验证表明，更改后的算法能够明显提高惯导系统在动基座下的姿态估计速度和精度，特别在周期性线振动环境下的对准精度能够提高一个数量级。多航次的湖试实验结果表明，改进后的算法能够有效提高航向对准精度，综合导航速度精度能够提高50%左右。

捷联惯导系统；晃动基座；初始对准；重力矢量

惯导系统的粗对准问题一直是惯性导航领域的关键性问题，传统解析式粗对准方法早已无法满足动态环境下对准的需求[1-7]。文献[8]通过计算重力矢量在惯性空间内旋转的角度，摆脱了对信噪比极低的地球旋转角速度的要求，解决了晃动基座下的对准问题，适用于水面系泊状态下舰船的对准需求，但当载体存在线运动情况时，无法消除由于运动产生的加速度和角速度，从而会产生对准误差。文献[9]在此基础上进一步考虑了载体线运动的影响，通过重新分解，提出了一种解决行进间粗对准的新方法。但在这些方法中，为了减小载体摇摆产生的加速度的干扰，使用了加速度积分来对重力积分进行平滑。由于求解方向余弦矩阵需要至少两组重力矢量在不同坐标系下的观测量，同时为了防止出现矩阵病态的问题，又需要这两组矢量不能过于平行，因此这就要求两组矢量积分的积分时间不能过于相近。权衡平滑效果和矢量夹角的要求，一般情况下会选择取和时刻的两组积分值（为对准时间），这种情况下，后时间内的计算过程对前时间内积分值没有帮助，这样便导致对重力信息的利用并不充分，结果也不是最优的。与此同时，积分计算使得整个tk时间内无法输出姿态信息，这对于系统实际应用来说是非常不方便的。针对以上缺点，本文将矩阵的求解过程转换为Wahba问题，实现对重力矢量信息的充分利用，并通过QUEST算法实现了晃动基座下行进间粗对准的最优算法。

1 晃动基座行进间对准算法

定义惯导系统载体坐标系，以航行器艏向为X正向，以垂直向上方向为Y正向，Z向定义满足右手定则，记为b系。惯导系统在上电时刻载体坐标系为，上电后在惯性空间内保持不动，其他坐标系定义如图1所示。

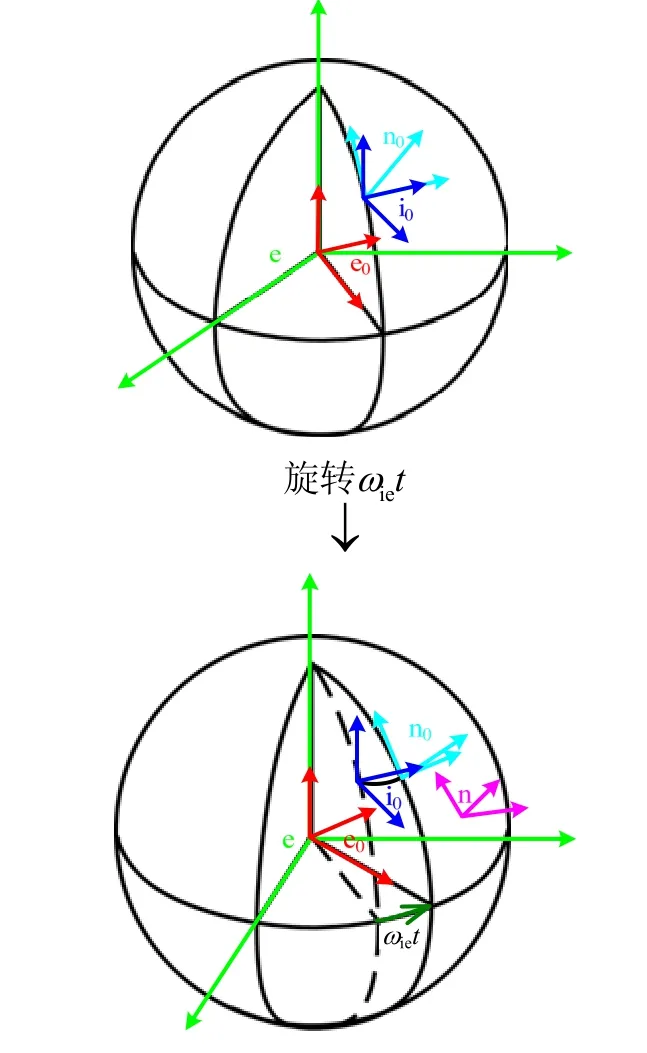
图1 坐标系转换关系示意图Fig.1 Schematic of coordinate transformation

粗对准的目的是求取对准结束时刻惯导系统载体坐标系b和导航坐标系n之间的转换关系。

初始对准姿态矩阵可分为两个矩阵相乘的形式：

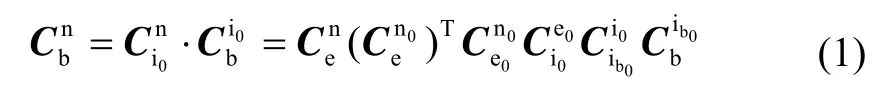
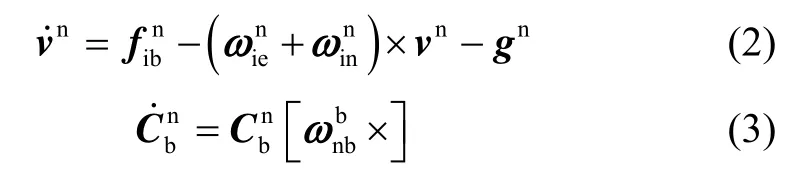
经转换可得：

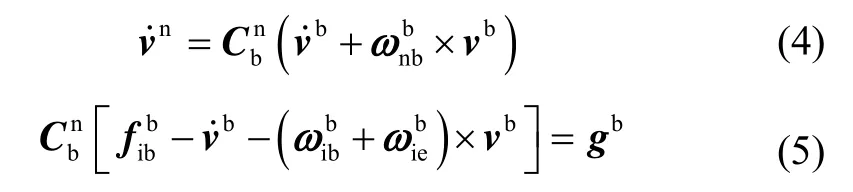
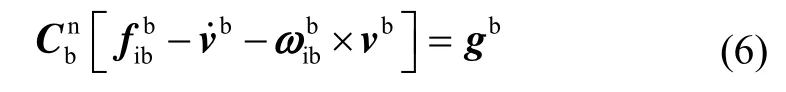
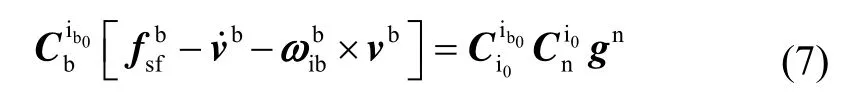
分别取当前时刻t以及时刻的积分值(t)、(t/2)、Vi0(t)和Vi0(t/2)构造正交矩阵，则有：

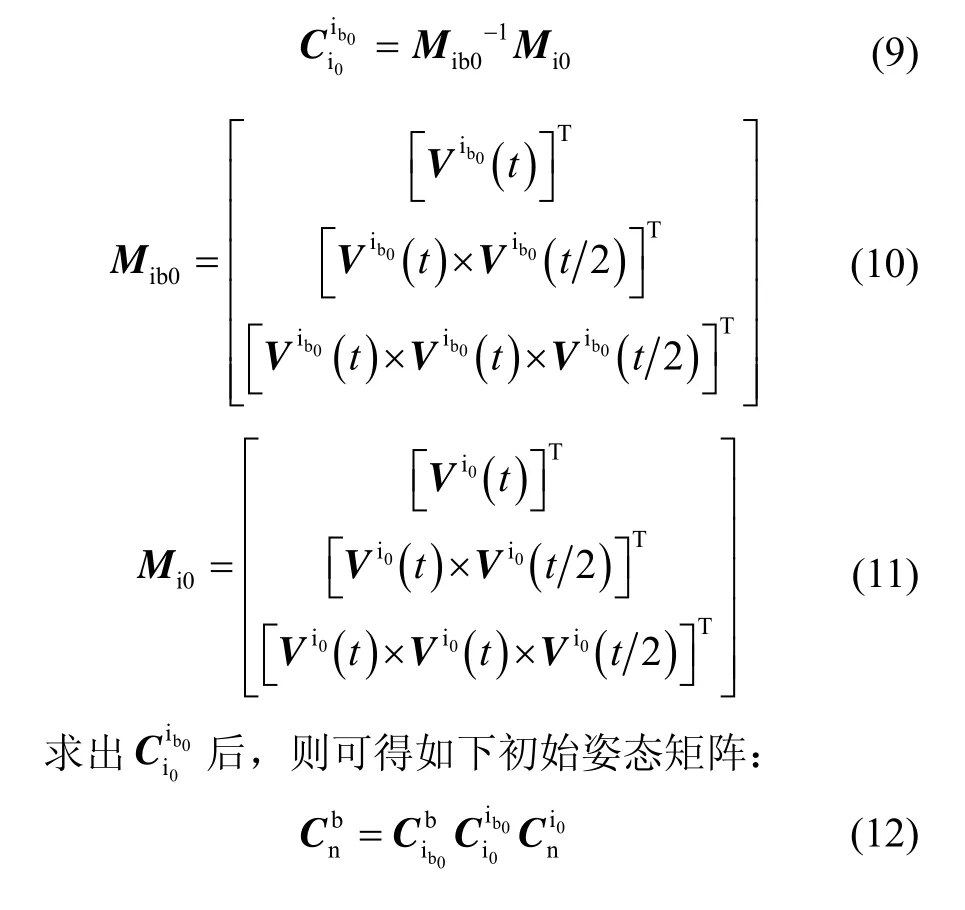
2 Wahba问题及QUEST算法

Wahba问题是Grace Wahba针对空间飞行器定姿问题提出的一种算法[10-11]，定义如下的最优估计：

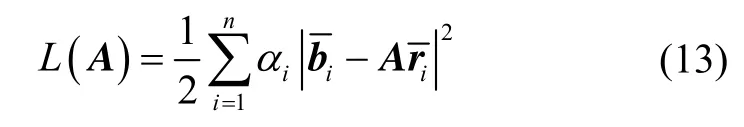
其中，A为所要求取的方向余弦阵，和为同一个矢量在两个坐标系下的测量值，αi为权重系数。

因此求L(A)最小值转变为求g(A)的最大值。

但是由于A包含9个元素，并且元素之间互相约束，直接求取A比较困难。因此转换思路，求取等效的四元数。四元数表示如下：

其中，为旋转轴，θ为旋转角度。

四元数的元素具有唯一约束：

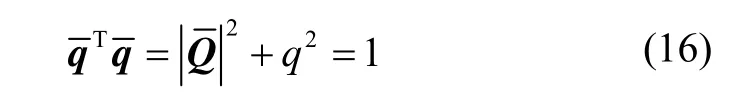
姿态矩阵A与四元数之间的转换关系为

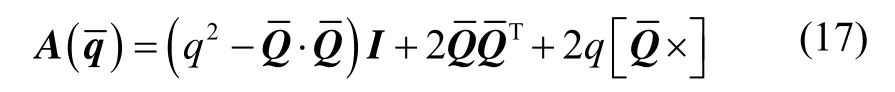
将式(17)带入式(14)中得：

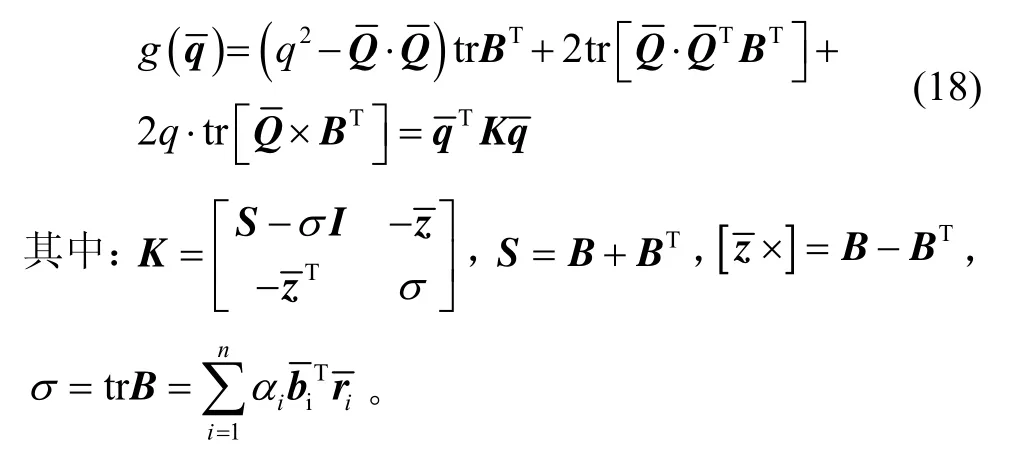
为了求取式(18)在约束条件(16)下的最大值，构建如下方程：

由此可知，λ是K的一个特征根，则是对应的特征向量。因此，当λmax为K的最大特征向量时，对应的特征向量为最优的四元数估计值。

根据算法的实时性要求，需要避免直接求取特征根和特征向量，QUEST算法便是其中一种递推算法。

将式(20)改写为如下形式：

根据Wahba问题原理可知，应该有λmax>>1，因此将λ0=1带入式(22)中，使用牛顿-拉夫逊法进行迭代：

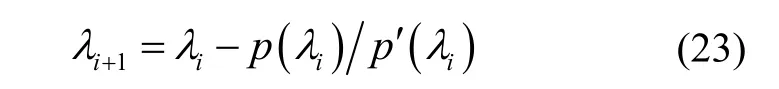
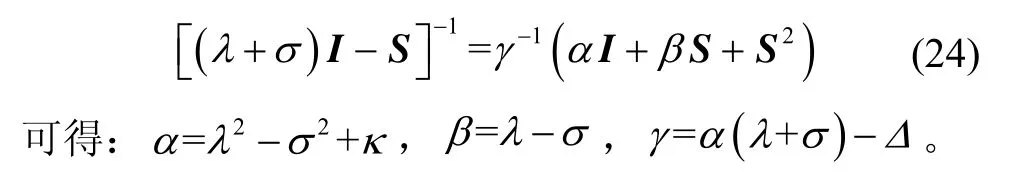
将α、β和γ带入式(22)和式(24)中，可以得到转换后的特征多项式：

可得姿态四元数的最优解为

3 仿真和试验验证

为了验证本文算法的效果，通过仿真和湖试试验对对准结果进行验证。

仿真条件为：参照第1节中载体系定义，以惯导系统z轴为中心轴摇摆，幅值10°，周期8 s；沿惯导系统x轴做线运动，0.1 m/s，周期5 s，系统对准过程曲线如图2所示（为了便于比较，在计算过程中保留了改进前算法的全部数值以显示对准过程中的姿态），姿态对准结果如表1所示。从对准结果可以看出，改进后的算法对姿态的估计要明显优于改进前的算法。

图2 仿真对准过程姿态曲线Fig 2 Attitude curve during alignment in simulation test

表1 仿真试验姿态对准误差Tab.1 Statistics of attitude error during alignment in simulation test

湖试试验共进行了3个航次，所使用的惯导系统为某光纤捷联惯导系统，精度指标为：陀螺漂移0.05 (°)/h，随机游走0.001(°)/h1/2；加速度计零位100μg，随机游走300μg/Hz1/2。其中一个航次的对准姿态曲线如图3所示；对准后开始航行，速度误差如图4所示。3个航次速度误差统计结果如表2所示。

航次1和航次3是在匀速直行情况下的对准结果，改进算法后系统的综合速度精度提高 42.2%。航次 2为存在随机加减速的情况，改进算法后系统的综合速度精度提高了56.7%。

图3 湖试对准过程姿态曲线Fig.3 Attitude curve during alignment in lake tes

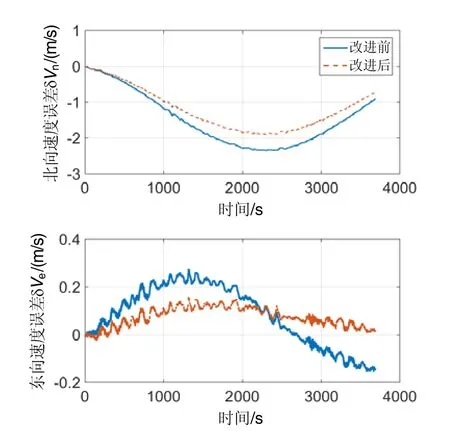
图4 湖试导航速度误差曲线Fig.4 Velocity error curve during navigation in lake test

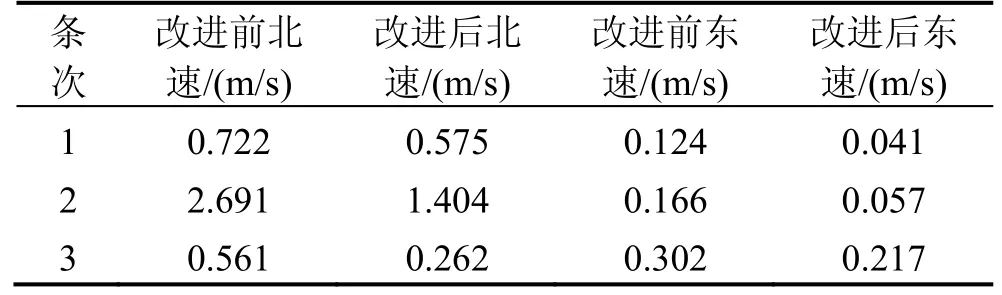
表2 湖试速度误差统计表（1σ）Tab.2 Statistics of velocity errors during navigation in lake test ( 1σ)

4 结 论

从仿真和湖试试验的结果可以看出，使用改进后的QUEST算法估计得到的姿态精度要明显高于改进前的算法，这是由于改进后的算法使用了整个对准过程中的全部信息，得到了最优估计，也因此使得惯导系统对线运动过程中的线振动干扰具有更强的鲁棒性，航向的收敛速度更快。虽然改进后的算法也是批处理算法，但是由于计算过程只需要计算各个变量的累加和，因此能够得到与递推算法相同的效果，能够满足实际系统对姿态的实时性需求。

（References）：

[1] Chang G. Robust Kalman filtering based on Mahalanobis distance as outlier judging criterion[J]. IEEE Transactions on Instrumentation and measurements, 2015, 64(3): 784-794.

[2] Liu Fei, Li Jie, Wang Haifu, et al. An improved quarternion Gauss-Newton algorithm for attitude determination using magnetometer and accelerometer[J]. Chinese Journal of Aeronautics, 2014, 27(4): 986-993.

[3] 王勇军, 徐景硕, 盛飞, 等. 基于最优三轴姿态测定算法的舰载惯导粗对准方法[J]. 中国惯性技术学报, 2013, 21(3): 294-297. Wang Yong-jun, Xu Jing-shuo, Sheng Fei, et al. Coarse alignment method based on optimized three-axis attitude determination algorithm for shipboard SINS[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 294-297.

[4] Wang B, Deng Z, Liu C, et al. Estimation of information sharing error by dynamic deformation between inertial navigation systems[J]. IEEE Transaction on Industrial Electronics, 2014, 61(4): 2015-2023.

[5] Chang L, Hu B, Li A, etal. Strapdown inertial navigation system alignment based on marginalised unscented Kalman filter[J]. IET Science, Measurement & Technology, 2013, 7(2): 128-138.

[6] Wu Xu, Sun Feng. Simulation study for FOG strapdowninertial navigation nonlinear alignment based on SVD-cubature Kalman filter[C]//Symposium on Photonics and Optoelectronics. Shanghai, 2012: 1-4.

[7] Hu Jie, Cheng Xiang-hong. A new in-motion initial alignment for land-vehicle SINS/OD integrated system [C]// 2014 Position, Location and Navigation Symposium. Monterey, CA, 2014: 407-412.

[8] 秦永元, 严恭敏, 顾冬晴, 等. 摇摆基座上基于信息的捷联惯导粗对准研究[J]. 西北工业大学学报, 2005, 23(5): 681-684. Qin Yong-yuan, Yan Gong-min, Gu Dong-qing, et al. A clever way of SINS coarse alignment despite rocking ship[J]. Journal of Northwestern Poly technical University, 2005, 23(5): 681-684.

[9] 严恭敏, 秦永元, 卫育新, 等. 一种适用于 SINS动基座初始对准的新算法[J]. 系统工程与电子技术, 2009, 31(3): 635-637. Yan Gong-min, Qin Yong-yuan, Wei Yu-xin etal. New initial alignment algorithm for SINS on moving base[J]. Systems Engineering and Electronic, 2009, 31(3): 635-637.

[10] Wahba G. A least squares estimate of satellite attitude[J]. SIAM Review, 1965, 7(3): 409-409.

[11] Markley F L, Crassidis J L. Fundamentals of spacecraft attitude determination and control[M]. New York: Springer New York, 2014.

[12] 刘义亭, 徐晓苏, 张涛, 等. 基于外参考速度辅助的行进间罗经法对准[J]. 中国惯性技术学报, 2015, 23(2): 165-171. Liu Yi-ting, Xu Xiao-su, Zhang Tao, et al. Compassing alignment in motion based on external reference velocity[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 165-171.

Application of quaternion estimator algorithm dedicated on alignment of swaying and moving carrier

GUO Yu-sheng1,2, FU Meng-yin1, DENG Zhi-hong1, ZHUANG Guang-chen2, DENG Liang2
(1. School of Automation, Beijing Institute of Technology, Beijing 100081, China;
2. Beijing Automation Control Equipment institute, Beijing 100074, China)

An optimal attitude estimation method with Quaternion Estimator based on gravity vectors is developed to solve the initial alignment problem of the inertial navigation system in swaying and moving carrier. Based on the traditional initial alignment method with gravity vectors, the process of solving the direction cosine matrix is converted to Wahba problem, which can make full use of the gravity vector information and realize the optimal algorithm for the coarse alignment of the swaying basement by Quaternion Estimator algorithm. Simulation and lake experiments demonstrate that the modified method can significantly increase the precision and rapidity of the attitude estimation and the precision of the heading alignment on a swaying and moving carrier. The precision can be increased by one order of magnitude on the carrier with periodically linear movement, and the overall velocity precision can be increased by 50%.

strapdown inertial navigation system; swaying base; initial alignment; gravity vectors

U666.1

A

1005-6734(2017)02-0182-04

10.13695/j.cnki.12-1222/o3.2017.02.008

2017-01-12；

2017-03-28

海装“十三五”预先研究课题（3020603030403）

郭玉胜 (1982—)，男，博士研究生，主要从事惯性系统及组合导航技术研究。E-mail: guoyusheng7209@139.com

联 系 人：付梦印（1964—），男，教授，博士生导师。E-mail: fumy@bit.edu.cn