基于黎曼与巴氏距离的脑磁图信号分类方法*

吴 煜，杨爱萍，章宦记，王 建，刘 立

天津大学 电子信息工程学院，天津 300072

基于黎曼与巴氏距离的脑磁图信号分类方法*

吴 煜+，杨爱萍，章宦记，王 建，刘 立

天津大学 电子信息工程学院，天津 300072

针对人脑对不同视觉目标刺激产生的脑磁图（magnetoencephalography，MEG）信号，提出了一种新型的脑磁图信号分类算法。该算法首先将滤波后的脑磁图信号投影到新的特征空间，然后将脑磁图信号投影后新特征的协方差特征投影到切线空间中，用协方差特征作为信号的特征，进而对样本进行预分类；接着将预分类的样本通过巴氏距离的调整，得到二次标记结果；最后采用黎曼距离对协方差特征矩阵在流形上进行调整，得到最终的分类结果。实验结果表明，该有监督与无监督相结合的算法有助于提高脑磁图信号分类的准确率。

脑磁图（MEG）；分类算法；协方差矩阵；黎曼距离；巴氏距离

1 引言

大脑活动会产生记录大脑活动的神经影像数据，分析在神经影像数据背后大脑对实际刺激的真实反应，称为脑解码（brain decoding），相关文献可以追溯至上世纪90年代[1-2]。在过去20多年的研究中，对脑解码的研究主要涉及三方面，即功能性磁共振成像（functional magnetic resonance imaging，fMRI）、脑电图（electroencephalograph，EEG）和脑磁图（magnetoencephalography，MEG）共三类信号。脑解码在这三类信号中问题的一般形式是，先对测试者给定外部的刺激，用设备记录测试者相应脑活动的神经影像数据；然后通过获得的神经影像数据，进行对应模型的训练；再通过训练得到的模型，分析当前测试者脑活动产生的波形所对应的神经状态。从早期的Wagner等人[3]通过功能性磁共振成像数据研究人类识别记忆的脑区域功能，到近些年Haynes等人[4]通过fMRI记录的脑活动数据分析人们阅读时的潜在意图，以及Tzovara等人[5]用电压图（voltage topographies）的方法解码外在视觉刺激与EEG信号间的对应关系，都取得了显著的成果。而MEG信号相关的研究有很多，有对疾病的研究[6-9]，比如Alonso等人[9]结合脑磁图，采用交叉互信息和光谱相干研究老年痴呆症；有对脑磁图信号源重建的研究[10-13]，如Lopez等人[10]采用贝叶斯模型对MEG信号进行信号源重建，Haufe等人[14]采用一种新型的复杂傅里叶系数对感觉运动皮层获取的脑磁波信号进行信号源的重建和定位；有对MEG信号解码的研究，近几年，Kauppi等人[15]研究了针对四类图像的视觉刺激对应的大脑活动状态，Olivetti等人[16]研究了对于人脸和刮去人脸的两类图的视觉刺激及相关的脑磁图对应的大脑活动状态。这些研究都取得了一系列重要的成果。

脑解码是指通过采集的脑信号来分析大脑受外界刺激所引发的神经状态。其解决框架一般是对信号进行预处理后，结合机器学习的办法，采用有监督的方法对信号进行分类，进而判断大脑对应的神经状态受何种刺激。相关的方法有Subasi等人[17]采用神经网络和逻辑回归的方法对正常人和癫痫病患者记录24小时8通道的EEG信号进行二分类；Chan等人[18]对于视觉和听觉刺激的语言任务，采用SVM（support vector machine）进行有监督的分类；Huttunen等人[19]采用正则化的多项式逻辑回归（regularized multinomial logistic regression）对MEG信号进行分类；Ford等人[20]采用Fisher线性判别（Fisher linear discriminant，FLD）的方法对阿尔兹海默症、精神分裂症和轻型颅脑损伤（mild traumatic brain injury，MTBI）三类患者的fMRI信号进行区分。

上述框架采用基于有监督的分类方法，过往的文献对于该问题或相关问题分析的一般框架是，分类器对信号进行检测后直接得到最终的分类结果。本文拟采用在有监督的预分类的基础上，引入类似无监督的方法，即采用巴氏距离和黎曼距离，对脑磁图信号进行调整分类。传统的方法注重从训练模型中判断未知数据的标记，而忽视了未知数据本身的结构特性对数据标记的作用。本文的贡献在于，将黎曼距离与巴氏距离这两种方法相结合，用于脑磁图信号分析，在有监督的传统机器学习方法的基础上结合数据自身特性，执行进一步的无监督调整。

本文组织结构如下：第1章简述脑磁图相关的应用与研究；第2章对本文的算法步骤进行详细描述；第3章采用本文算法对数据进行结果分析；第4章总结全文。

2 基于黎曼距离与巴氏距离的分类算法

本文采用的算法步骤如下：第一步，用SVM和Lasso方法对已有MEG数据集进行预标记；第二步，用无监督方法改进预测结果。对数据进行预标记前，对脑磁图信号进行了滤波处理。

2.1 预标记样本

脑磁图数据样本是包含多通道和多时间采样点的高度冗余信号，可通过对信号降维以压缩冗余信息[17，21-23]，提高后续的处理效率。本节首先设计线性滤波器，在抑制原始信号噪声的同时对信号进行降维，其次构造滤波信号的协方差矩阵作为进一步分析时的输入特征，最后用SVM和Lasso方法对样本进行标记。

2.1.1 空域滤波

具有N通道T时间点的采样信号x∈RN×T可以看作是大脑内部S个信号源s∈RS×T和噪声信号n的混合，其过程可以表达为：

其中，W∈RN×S是转换矩阵；n是零均值独立同分布噪声向量。考虑到采集信号的冗余性，可认为S＜N。由式（1），对采集信号逆变换可得到降维的信号。然而实际中变换矩阵未知，因此借助xDAWN算法[24]来获得低维度信号，即构造一组线性滤波器U，使得滤波后的无噪信号与有噪信号的比值最大，即：

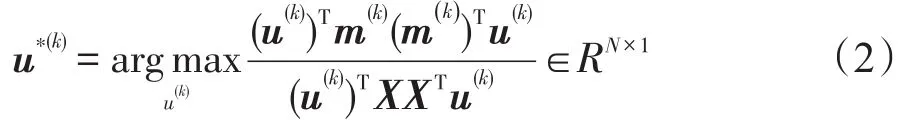
其中，无噪信号由同类测试信号均值 m(k)∈RN×T，k∈{0,1}来近似，而X=[x1,x2,…,xn]是测试者采集到的所有数据样本的联合矩阵。对于每类刺激，对式（2）采用特征值-特征向量的方法求解的特征值和特征向量，选择最大的m个特征值对应的特征向量构造矩阵，进而获得变换矩阵U=[u(0),u(1)]∈RN×2m。而降维后的信号s为：

而新的均值为ms=Um。

2.1.2 滤波后数据的协方差矩阵表示

2000年，Seung等人[25]在Science上发表文章提出感知可能以流形存在。流形是局部具有欧氏空间性质的空间，而采样的二维数据的协方差矩阵满足正定对称条件，具有黎曼度量的特性。协方差矩阵是二维采样数据在黎曼空间中表现的形式，协方差矩阵所在的空间便是黎曼空间。两个协方差样本在黎曼空间中的距离定义为[26]：

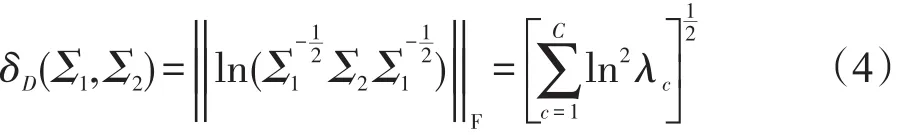
采样数据的协方差矩阵为：

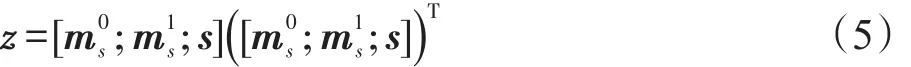
为适应进一步的预测操作，采用切线空间映射[26]的方法将协方差矩阵z从黎曼空间映射到欧氏空间：

式（6）求出在黎曼空间上协方差矩阵z的均值zmean，对于所有的协方差矩阵，可按照下式计算：

取s的上三角产生一维向量作为输入特征变量。

2.1.3 使用标记数据的有监督方法

本文假定预测信号正负样本比例已知，改进组合回归模型用于样本标记预测。为此以h为输入特征，利用有标记数据集分别训练SVM和Lasso两种回归模型。

预测时，将全部样本对SVM和Lasso的回归模型G1、G2的结果相加，在所有输出值中根据两类样本的比例选取阈值α1，得到预测的标记：

2.2 使用标记数据的无监督方法

对于预分类训练的模型，每一个测试者产生的脑磁图数据的分布是不相同的[16]，因此产生的模型只能对样本进行一个大致的分类；而更加精确的分类，需要在第一次分类的基础上结合其他方式，来挖掘测试样本的内在特性，以进行重新调整。

本文假定数据在某个空间上存在着区别，在该空间上结合预标记的结果，对预标记的样本分别采用巴氏距离和黎曼距离调整，充分挖掘样本数据的内在特征，从而对预标记的结果进行重新调整。

2.2.1 采用巴氏距离更新预标记样本

用样本到两类中心的巴氏距离重新对样本分类。巴氏距离在距离度量的时候考虑类的均值和方差的统计特征，可用来对两类样本的相关性进行测量，对预标记的样本衡量每个样本与两类预标记样本中心点的相关性，能够重新调整样本的标记。

巴氏距离对类的可分离性有比较好的度量[27]效果。对于给定的样本特征h，巴氏距离通过度量每一个特征，对所有的特征度量结果进行求和来调整预先标记的样本类别。

为了较精确地得到两类样本的中心点，对预标记的样本h，随机进行多次测试样本的抽取操作，每次抽取比例一定的两类预标记样本，根据抽取的两类样本比例分别计算每次两类样本中每个特征的阈值。对多次阈值的结果计算每个特征阈值的均值和方差。这些方差和均值分别为，其中 μ1表示预标记为1的样本特征均值，表示预标记为1的样本特征方差，μ2表示预标记为0的样本特征均值，表示预标记为0的样本特征方差。对每一个特征，按照如下步骤计算。

步骤1计算：

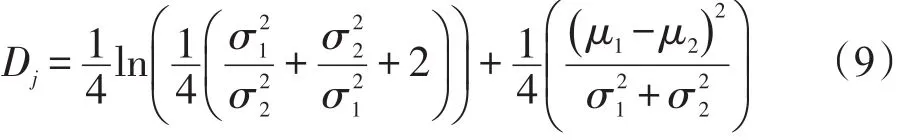
其中，j∈{1,2,…,l}，l为方差和均值向量的长度；Dj表示对一个特征的权值。

步骤2采用巴氏距离计算特征向量与两类样本中心之间的相似度：

步骤3将结果Dis根据测试样本比例选出阈值α2；若大于阈值的计算结果，将相对应的样本重新标记为1，否则标记为0：

2.2.2 采用黎曼距离更新巴氏距离标记结果

巴氏距离衡量样本与中心点间的相似度采用的是欧氏空间中距离度量的方式，为了区分样本间的相似度，这种度量方法仅仅对特征进行简单的权重求和。但针对特征实际的空间分布对分类的影响，因为与欧氏空间相比，MEG信号特征实际的空间分布在黎曼流形上更容易区分，所以巴氏距离体现得不是很好。因此在黎曼空间上运用黎曼几何分析方法，采用黎曼距离对样本进行聚类。

对于采用巴氏距离进行第二次标记的测试样本，首先结合测试样本标记信息，仅对测试样本进行空间和时间上的降维，用式（1）～（6）得到第二次标记的测试样本的协方差矩阵Σ；其次，分别计算标记为1和0的测试样本协方差矩阵的黎曼均值，得到Σ(1)和 Σ(0)：

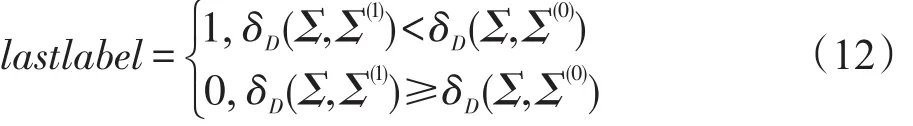
重复上述步骤若干次，得到最终的测试样本标记结果。

3 实验结果

3.1 实验1

采用The ATTEND projec（tcharacterizing and improving brain mechanisms of attention）数据集，该脑磁图数据记录了大脑对不同视觉目标的响应，记录了测试者看到人脸图像和刮去人脸图像时的大脑活动信号。测试采用了306通道全头型脑磁图系统，其中204个通道是倾斜计（gradiometer）传感器测量通道，102个通道是磁力计（magnetometer）传感器测量通道。每个测试样本的脑磁图记录时间是1.5 s，其中刺激的信号产生前0.5 s，刺激后的时间1 s。单个通道脑磁图信号的采样率是250 Hz，有375个采样点。一个测试样本共306×375个采样数据。本文采用刺激后0.5 s的数据，即一个测试样本306×125个采样数据。实验中每个测试者平均采集了588个样本，人脸和刮去人脸图像各半。整个数据集包括16个测试者，9 414个样本。

将数据集分成训练样本集和测试样本集，对每个样本信号依次采用50 Hz的带陷滤波器、100 Hz的低通滤波器、均值滤波器进行滤波。对构成训练样本集的15个测试者，每个测试者提取一组降维参数，共计15组参数。所有16个测试者（15个做训练和1个做测试）的样本在15组参数映射下得到新的特征，对新的特征空间下的数据集，采用SVM和Lasso组合进行分类，并对测试样本集进行对应的预分类标记1或0。对预分类标记后的测试样本集，采用巴氏距离在新的特征空间下对测试样本进行第二次标记。对第二次标记后的测试样本集，采用黎曼距离对测试样本进行若干次重复迭代标记，得到最终的标记结果。

当迭代前后两个类别标记的误差小于0.1%时，即认为已迭代至收敛。通过修改迭代次数，发现迭代7次以上时即收敛，迭代次数与分类正确率的曲线如图1所示。其中，迭代0次代表标记只经过巴氏距离而未经过黎曼距离的处理。

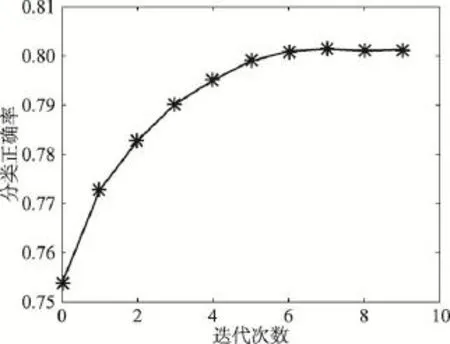
Fig.1 Relationship between classification accuracy and iterations图1 分类正确率与迭代次数的关系曲线

本文采用的算法得到的实验结果如表1所示。表1的第一列表示16个测试者中每一位个体都要作为训练集；表1的第二列表示对每个测试者预分类的正确率；表1的第三列表示对每个测试者使用巴氏距离调整后分类的正确率；表1的第四列表示对每个测试者使用黎曼距离调整后分类的正确率。

Table 1 Experimental results表1 实验结果

该数据集来源于著名数据分析竞赛网站Kaggle举办的关于视觉目标刺激的脑磁图信号分类比赛，因此将本文的实验结果与此次比赛中前几名选手的成绩进行比较。在本次比赛中，第一名的交叉验证的测试正确率为73.6%，第二名的交叉验证的测试正确率为75.8%，而本文采用的算法显著地提高了测试的正确率，为80.1%。第一名的算法先采用Lasso、SVM、TrSVM分类器融合对测试样本进行预标记，之后用巴氏距离对306×375个特征进行重新标记，但是该算法仅TrSVM分类器的训练时间就需要16个小时左右，而本文所有代码的运行时间不足1个小时；同时第一名对预标记的结果采用306×375个特征进行标记，导致样本维度过高，从而难以提取有效的特征，而本文仅对2 000多个特征向量进行调整；同时，由表1可知，使用本文算法时，即便仅用巴氏距离标记所得的结果是75.4%，也略高于第一名的交叉验证结果，况且本文基于黎曼距离的分类准确率为80.1%；因此，能够看出，尽管第一名的TrSVM分类器的效果比起SVM和Lasso会有所提升，但是其总体交叉验证的准确率与本文算法比起来还是稍逊一筹。第二名算法对输入的样本直接采用了刺激后1 s的数据，输入的样本维度306×250远远高于本文的输入样本维度。

3.2 实验2

本文还在另外一个脑磁图数据库[28]上验证了算法性能，该数据库记录了一个测试者连续两天观看5类不同的无声视频时，对各类视频图像刺激所产生的脑磁图信号。5类视频分别是Artificial、Nature、Football、Bean和Chaplin，记录的脑磁图数据样本大小是204×200，其中204为采用倾斜磁力计的通道个数，200为每一类样本在1 s周期内的采样点数，即采样率。同时该数据库还提供了5个子数据库，分别是对原始数据经过带通滤波后，中心频点为2、5、10、20和35 Hz的数据库。针对该数据库，采用试验者第一天的数据，预测测试者第二天数据对应的刺激类别。

Huttunen等人[19]采用正则化的多分类逻辑回归算法，对Bean和Chaplin类别区分的正确率达到96.5%；在ICANN’11比赛中，对于Bean和Chaplin类别区分的正确率最高能达到97.1%；而本文采用中心频率为2 Hz，带宽为3 Hz的5阶巴特沃思滤波器，先对原始脑磁图信号进行滤波，最终本文算法对Bean和Chaplin类别区分的正确率能够达到99.2%。因此，在本数据集所代表的脑磁图信号的二分类问题方面，本文算法也是较优的。

4 总结

本文提供了一种对脑磁图信号分类的新算法，将基于SVM和Lasso的有监督分类和基于黎曼几何和巴氏距离的无监督分类相结合，显著地提高了检测结果。

本文较重要的因素是预处理滤波器的选择，滤波器的有效选择能够滤除无关信号和噪声信号，提取有效的信号，并提高预分类的正确率。比如Xu等人[29]研究语言刺激对精神分裂所涉及不同频率段α（8～13 Hz）与β（13～30 Hz）对数据特征的有效选择。Shyu等人[30]研究稳态视觉诱发电位（steady-state visual evoked potential，SSVEP）信号时采用三阶的低通巴特沃思滤波器和高通的滤波器组合选择20～26 Hz的频段信号。本文对实验1的数据库采用3种滤波器相结合的方法进行滤波，该滤波器的目的是为了提取20 Hz以下的脑磁波频段信号，而实验2采用巴特沃思滤波器是为了提取0.5～3.5 Hz的频段信号。对于实验1，当采用的滤波器包含有高频段信号或采用巴特沃思滤波器0.5～20 Hz时，取得的效果都比实验1采用的这3种滤波器的组合效果差。对于实验2，当采用中心频率分别为5 Hz、10 Hz、15 Hz、30 Hz，带宽为3 Hz的5阶巴特沃思滤波器时，效果也不如中心频率为2 Hz，带宽为3 Hz的5阶巴特沃思滤波器；而不滤波，直接对信号采用本文所设计的算法，实验2的正确率为89.6%。

本文基于有监督的学习方式，并且采用Lasso和SVM相结合的形式对样本进行预分类。采用Lasso和SVM组合最终的测试正确率可以达到80.11%，而Lasso最终的测试正确率是79.77%，SVM最终的测试正确率是79.65%，最终分类效果都略逊于两者组合的效果。可能的原因是，Lasso对样本进行的模型训练是在原始特征的基础上，使对预测结果影响小的特征对应的权值为0；而SVM的模型训练是在原始特征的基础上，将原始特征映射到更高维的空间上进行区分，两种不同属性的线性分类方式可能优势互补，提升最终的测试结果。

由于不同的测试者之间的脑磁图信号差异较大，就目前的脑磁图信号分类的研究进展而言，难以给出一般性的阈值计算方法，故阈值通常是取一个与数据特性相关的经验值。该数据集是由不同的测试者在观看两类不同的图像（脸部图像/残缺的脸部图像）时采集的脑磁图信号而得来，该数据集的特性便导致问题成为一个二分类问题；同时在此二分类问题中，该数据集整体所带的先验是两类图像产生刺激信号相对应的实验次数；假定在后续过程中作为标记分类准则的阈值α1与α2与该数据集整体所隐含的两类的分布比例有关。又由于只知道16位测试者总体的正负类比例，而不知每个测试者的具体正负类比例，因此阈值的选取可根据总体样本中的正负类比例而定。

本文的另一个问题是降维。采用Pires等人[31]在P300诱发电位的脑机接口技术中采用的降维方法对脑磁图信号进行空间和时间的降维。在空间降维过程中采用特征值特征向量的方式对进行求解。该矩阵不是正定对称的，因此所求的特征值和特征向量可能存在复数，导致特征向量h也会存在复数；而Lasso作为分类算法，输入的信号需要为实数，因此在本文的实验中特征向量h需要去除复数部分的特征，剩下的实数部分特征作为Lasso和SVM的输入，实际h输入的大小是1 600维。对数据采用6阶巴特沃思滤波器滤除信号后，采用特征值特征向量求解没有出现复数的情况。不同滤波器的性能会导致最终处理结果的不同。后续的研究应对式（2）求解的方式做深入探讨。同时在本文中，降维后需要选择特征值最大的4项特征向量，而若选择更多的几项或选择特征值实数项最大的几项组成线性投影空间U，对分类结果会有怎样的影响，都有待进一步的研究。

本文算法对两种类别信号的检测能够得到比较好的效果，对多类别信号的检测与自适应阈值的计算问题还需要进行深入的研究。但本文算法可以应用于其他与脑磁图像类似的数据库，比如脑电图数据、心电图数据、功能性神经影像数据等。

[1]Kippenhan J S,Barker W W,Pascal S,et al.Evaluation of a neural-network classifier for PET scans of normal and Alzheimer's disease subjects[J].Journal of Nuclear Medicine, 1992,33(8):1459-1467.

[2]Mørch N,Hansen L K,Strother S C,et al.Nonlinear versus linear models in functional neuroimaging:learning curves and generalization crossover[C]//LNCS 1230:Proceedings of the 15th International Conference on Information Processing in Medical Imaging,Poultney,USA,Jun 9-13,1997. Berlin,Heidelberg:Springer,1997:259-270.

[3]Wagner A D,Desmond J E,Glover G H,et al.Prefrontal cortex and recognition memory functional-MRI evidence for context-dependent retrieval processes[J].Brain,1998, 121(10):1985-2002.

[4]Haynes J D,Sakai K,Rees G,et al.Reading hidden intentions in the human brain[J].Current Biology,2007,17(4): 323-328.

[5]Tzovara A,Murray M M,Plomp G,et al.Decoding stimulusrelated information from single-trial EEG responses based on voltage topographies[J].Pattern Recognition,2012,45(6): 2109-2122.

[6]Gomez C,Hornero R,Abasolo D,et al.Study of the MEG background activity in Alzheimer's disease patients with scaling analysis methods[C]//Proceedings of the 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society,Minneapolis,USA,Sep 3-6,2009. Piscataway,USA:IEEE,2009:3485-3488.

[7]Anzellotti F,Franciotti R,Onofrj M.Temporal recruitment of cortical network involved in reading epilepsy with paroxysmal alexia:a combined EEG/MEG study[J].Seizure,2013, 22(2):156-158.

[8]Miao Ailiang,Xiang Jing,Tang Lu,et al.Using ictal highfrequency oscillations(80-500Hz)to localize seizure onset zones in childhood absence epilepsy:a MEG study[J].Neuroscience Letters,2014,566(18):21-26.

[9]Alonso J F,Poza J,Mañanas M A,et al.MEG connectivity analysis in patients with Alzheimer's disease using cross mutual information and spectral coherence[J].Annals of Biomedical Engineering,2011,39(1):524-536.

[10]López J D,Litvak V,Espinosa J J,et al.Algorithmic procedures for Bayesian MEG/EEG source reconstruction in SPM[J].NeuroImage,2014,84(1):476-487.

[11]Fukushima M,Yamashito O,Knosche T R,et al.MEG source reconstruction based on identification of directed source interactions on whole-brain anatomical networks[J]. NeuroImage,2015,105:408-427.

[12]Strobbe G,van Mierlo P,De Vos M,et al.Multiple sparse volumetric priors for distributed EEG source reconstruction [J].NeuroImage,2014,100:715-724.

[13]Zhang Jian,Liu Chao,Green G.Source localization with MEG data:a beamforming approach based on covariance thresholding[J].Biometrics,2014,70(1):121-131.

[14]Haufe S,Tomioka O R,Dickhus T,et al.Large-scale EEG/ MEG source localization with spatial flexibility[J].Neuro-Image,2011,54(2):851-859.

[15]Kauppi J P,Parkkonen L,Hari R,et al.Decoding magnetoencephalographic rhythmic activity using spectrospatial information[J].NeuroImage,2013,83(12):921-936.

[16]Olivetti E,Kia S M,Avesani P.MEG decoding across subjects[C]//Proceedings of the 4th International Workshop on Pattern Recognition in Neuroimaging,Tubingen,Germany, Jun 4-6,2014.Piscataway,USA:IEEE,2014:1-4.

[17]Subasi,A,Gursoy M I.EEG signal classification using PCA,ICA,LDA and support vector machines[J].Expert Systems withApplications,2010,37(12):8659-8666.

[18]Chan A M,Halgren E,Marinkovic K,et al.Decoding word and category-specific spatiotemporal representations from MEG and EEG[J].NeuroImage,2011,54(4):3028-3039.

[19]Huttunen H,Manninen T,Kauppi J P,et al.Mind reading with regularized multinomial logistic regression[J].Machine Vision andApplications,2013,24(6):1311-1325.

[20]Ford J,Farid H,Makedon F,et al.Patient classification of fMRI activation maps[C]//LNCS 2879:Proceedings of the 6th International Conference on Medical Image Computing and Computer-Assisted Intervention,Montréal,Canada,Nov 15-18,2003.Berlin,Heidelberg:Springer,2003:58-65.

[21]Hassanien A,Vorobyov S A.A robust adaptive dimension reduction technique with application to array processing[J]. IEEE Signal Processing Letters,2009,16(1):22-25.

[22]Haufe S,Dähne S,Nikulin V V.Dimensionality reduction for the analysis of brain oscillations[J].NeuroImage,2014, 101:583-597.

[23]Barachant A,Bonnet S,Congedo M,et al.Classification of covariance matrices using a Riemannian-based kernel for BCI applications[J].Neuro Computing,2013,112:172-178.

[24]Rivet B,Souloumiac A,Attina V,et al.xDAWN algorithm to enhance evoked potentials:application to brain-computer interface[J].IEEE Transactions on Biomedical Engineering,2009,56(8):2035-2043.

[25]Seung H S,Lee D D.The manifold ways of perception[J]. Science,2000,290(5500):2268-2269.

[26]Barachant A,Bonnet S,Congedo M,et al.Multiclass braincomputer interface classification by Riemannian geometry [J].IEEE Transactions on Biomedical Engineering,2012, 59(4):920-928.

[27]Coleman G B,Andrews H C.Image segmentation by clustering[J].Proceedings of the IEEE,1979,67(5):773-785.

[28]Klami A,Ramkumar P,Virtanen S,et al.ICANN/PASCAL2 challenge:MEG mind reading-overview and results[C]//Proceedings of the International Conference on Artificial Neural Networks and Sponsored by the PASCAL2 Challenge Programme,Espoo,Finland,Jun 14-17,2011:3-19.

[29]Xu Tingting,Stephane M,Parhi K K.Classification of singletrial MEG during sentence processing for automated schizophrenia screening[C]//Proceedings of the 6th International IEEE EMBS Conference on Neural Engineering,San Diego,USA,Nov 6-8,2013.Piscataway,USA:IEEE,2013: 363-366.

[30]Shyu K K,Chiu Y J,Lee P L,et al.Total design of an FPGA-based brain-computer interface control hospital bed nursing system[J].IEEE Transactions on Industrial Electronics, 2013,60(7):2731-2739.

[31]Pires G,Nunes U,Castelo-Brancob M.Statistical spatial filtering for a P300-based BCI:tests in able-bodied,and patients with cerebral palsy and amyotrophic lateral sclerosis [J].Journal of Neuroscience Methods,2011,195(2):270-281.

WU Yu was born in 1992.He is an M.S.candidate at Tianjin University,and the student member of CCF.His research interests include digital image processing,pattern recognition and machine learning,etc.

吴煜（1992—），男，甘肃兰州人，天津大学视觉模式分析实验室硕士研究生，CCF学生会员，主要研究领域为数字图像处理，模式识别，机器学习等。

YANG Aiping was born in 1977.She received the Ph.D.degree in signal and information processing from Tianjin University in 2008.Now she is an associate professor at Tianjin University.Her research interests include digital image processing,pattern recognition and machine learning,etc.

杨爱萍（1977—），女，山东聊城人，2008年于天津大学获得博士学位，现为天津大学视觉模式分析实验室副教授，主要研究领域为数字图像处理，模式识别，机器学习等。发表学术论文30余篇，发表译著3部，获授权发明专利2件，主持国家自然科学基金（面上项目）1项，国家自然科学基金（青年项目）1项。

ZHANG Huanji was born in 1990.He is an M.S.candidate at Tianjin University.His research interests include digital image processing,pattern recognition and machine learning,etc.

章宦记（1990—），男，浙江温州人，天津大学视觉模式分析实验室硕士研究生，主要研究领域为数字图像处理，模式识别，机器学习等。获授权发明专利2件。

WANG Jian was born in 1976.He received the Ph.D.degree in communication and information system from Shanghai Jiao Tong University in 2006.Now he is a lecturer at Tianjin University,enterprise post-doctor in National Ocean Technology Center,and the member of CCF.His research interests include digital image processing and computational photogrammetry,etc.He has published more than 20 papers,hosted the youth program of National Natural Science Foundation,and participated in National Natural Science Foundation project as main participant.

王建（1976—），男，山东济南人，2006年于上海交通大学获得博士学位，现为天津大学讲师，国家海洋技术中心在站企业博士后，CCF会员，主要研究领域为数字图像处理，计算摄影学等。发表学术论文20余篇，主持并完成国家自然科学基金（青年项目）1项，参与国家自然科学基金（面上项目）3项。

LIU Li was born in 1975.He received the Ph.D.degree in color signal processing from Illinois Institute of Technology in 2005.His research interests include real-time data perception and visualization,pattern recognition and machine learning,etc.

刘立（1975—），男，湖北荆州人，2005年于美国伊利诺伊理工大学获得博士学位，主要研究领域为实时数据感知与可视化，模式识别，机器学习等。发表学术论文30余篇。

MEG Signals Classification Algorithm Based on Riemann and Bhattacharyya Distances*

WU Yu+,YANGAiping,ZHANG Huanji,WANG Jian,LIU Li
School of Electronic and Information Engineering,Tianjin University,Tianjin 300072,China

+Corresponding author:E-mail:gorbachev@tju.edu.cn

WU Yu,YANG Aiping,ZHANG Huanji,et al.MEG signals classification algorithm based on Riemann and Bhattacharyya distances.Journal of Frontiers of Computer Science and Technology,2017,11(5)：776-784.

This paper proposes a new algorithm on MEG(magnetoencephalography)signals to classify MEG signals generated when human brain confronts the stimulation of different visual objects.At first,filtered MEG signals are projected to a new feature space and they will generate new features.The covariance features of new features,on behalf of the MEG signals features,will be used to presort samples in a vector space named tangent space.Then,the second time labeling results can be derived after adjusting prelabeled samples using Bhattacharyya distance.Finally, the ultimate classification results can be got by applying the Riemann distance method to adjust covariance matrices in manifold.The extensive experiments show that the combination of supervised and unsupervised algorithms can remarkably improve the classification accuracy of MEG signals.

magnetoencephalography(MEG);classification algorithm;covariance matrices;Riemann distance; Bhattacharyya distance

10.3778/j.issn.1673-9418.1603090

A

TP391

*The National Natural Science Foundation of China under Grant Nos.61372145,61172121,61002030,61002027(国家自然科学基金).

Received 2016-03,Accepted 2016-07.

CNKI网络优先出版:2016-07-01,http://www.cnki.net/kcms/detail/11.5602.TP.20160701.1646.008.html