边缘覆盖去重的社交网络影响力最大化算法*

胡 敏，孙欣然，黄宏程,2+

1.重庆邮电大学 通信与信息工程学院，重庆 400065

2.重庆大学 计算机学院，重庆 400044

边缘覆盖去重的社交网络影响力最大化算法*

胡 敏1，孙欣然1，黄宏程1,2+

1.重庆邮电大学 通信与信息工程学院，重庆 400065

2.重庆大学 计算机学院，重庆 400044

社交网络；影响力最大化；边缘贡献；启发式算法

1 引言

人们因共同学习、生活、工作，形成了不同圈中的复杂社交关系，人与人在现实生活中的交往形成了线下的社交网络，这便是复杂社交网络的开端。随着互联网的普及和高速发展，人们获取信息的方式和途径从以前的报刊、杂志、电视等扩展到了互联网之中，他们复杂的社会交往关系也从现实社会延伸到虚拟网络之中，形成了线上的社交网络。

Domingos等人[1]在2001年提出节点影响力最大化问题，之后该问题便得到了极大的关注。随着社交网络的兴起，网络监管与舆论引导控制变得越来越重要。此外，互联网社交网络中的用户数激增，商家逐渐趋向于在社交网络这个巨大的平台上发布广告信息，进行商品的推广营销。从根本上说，舆论引导和商品推广是特定价值信息在社交网络平台上的最大范围扩散，其中一个关键问题是如何选取网络中这些信息传播影响力最大的节点集，也就是影响力最大化问题，这也一直是研究的热点和难点。

Kempe等人[2]提出爬山贪心算法Basic-greedy，这是针对节点影响力最大化问题最初始的解决方案。由于贪心算法的时间复杂度过高，不适用于大规模网络。针对该问题，研究者对算法进行了改进优化[3-6]，提出了CELF（cost-effective lazy forward）、CELF++、New-greedy、Mix-greedy等算法。这些改进算法虽提高了时间效率，但对于大规模网络仍然不能适用。为了研究大规模网络中的节点影响力最大化问题，启发式算法应运而生。启发式算法通常具有运行时间短的特点，但算法准确度相对较差，传播范围相对较小。阶段式算法是贪心算法与启发式算法的综合型算法[7-9]，通常在算法初始选取阶段采用启发式思想评估节点影响力，后续采用贪心算法细化选取。

社交网络中通常节点数量多，关系连边复杂，属于大规模复杂网络，贪心算法难以满足目前大规模社交网络的要求，因此本文采用启发式算法的思想。针对启发式算法中传播影响范围相对较小的问题，本文考虑节点全局结构信息和邻近结构信息两方面来评估节点影响力，发现并解决了边缘节点影响范围重合问题，提出了基于边缘覆盖去重的启发式算法（edge cover algorithm，ECA）。

本文组织结构如下：第2章介绍了相关工作；第3章研究了基于边缘覆盖去重的影响力最大化算法；第4章给出了实验结果及分析；第5章对本文工作进行总结。

2 相关工作

2.1 传播模型

在寻找特定网络中的影响力节点集时，需要借助相应的传播模型。一般将社会网络抽象为有向图G(V,E)，将用户抽象为节点，V表示网络中所有节点的集合；将用户之间的连接关系抽象为连边，E表示网络中所有连边的集合。目前常用的传播模型有线性阈值模型（linear threshold model，LT）[10]和独立级联模型（independent cascade model，IC）[11]。在这两种模型中，网络中的节点存在活跃或非活跃两种状态且只处于其中之一，节点可以从非活跃状态转变为活跃状态，反之则不成立。本文选取独立级联模型作为传播模型，并对其进行详细介绍。

IC模型假设一个活跃节点尝试激活其每个邻居节点的机会有且只有一次，若激活失败，则对其失去影响力，且每一次激活行为的激活概率相对独立。假设A为初始活跃节点集，活跃节点的传播规则如下：

（1）非活跃节点v的邻居节点u在传播的t时刻尝试激活节点v，且u激活v的概率为pu,v。

（2）若v被激活，则v的v+1时刻转换为活跃节点；反之，v的状态不发生改变。

（3）不断重复上述过程，当网络中的活跃节点都没有影响力时，传播结束。

2.2 启发式算法研究

基于Random、Degree、Centrality的算法[2]是启发式算法最基本的算法。常见的权威算法包括陈卫等人提出的Degree-discount、基于最大影响力子树的PMIA（prefix excluding maximum influence arborescence）启发式[12]、基于有向无环图的LDAG（labeled directed acyclic graph）启发式[13]以及Jung等人提出的综合效果最优的IRIE（influence ranking influence estimation）启发式[14]等。很多人针对这些算法进行了改进，并且取得了更优的效果。2010年，Kitsak等人[15]提出了k-core算法来评估节点的传播影响力，并且提出了基于覆盖的最大核算法和最大度算法。2011年，Goyal等人[16]分析了LDAG算法的不足，针对LDAG算法中存在的影响力路径忽略的问题进行改进，提出了基于节点影响力的简单路径SIMPATH启发式算法。2015年，曹玖新等人[17]提出了一种基于 k-core的影响力最大化算法（core covering algorithm，CCA），算法结合k-core算法和度中心性求出每个节点的影响力，对节点的影响半径（d=1和d=2）进行了讨论。

相比于贪心算法，启发式算法的求解时间具有较大优势，但其算法准确度较差，因此提高算法准确度是启发式算法研究的长期目标。

在以上提到的影响力最大化启发式算法研究中忽略了影响范围重合问题。一些考虑影响范围重合的覆盖类算法研究也并没有考虑边缘贡献的问题。针对这一问题，本文在考虑边缘贡献的条件下研究了影响力最大化算法。

3 基于边缘覆盖去重的影响力最大化算法

本文采用启发式算法的思想，在IC模型的基础上，提出了基于边缘覆盖去重的启发式算法ECA。该算法考虑节点全局结构信息和邻近结构信息两方面来评估节点影响力，并通过去除已选节点影响范围内的所有节点的方式来屏蔽已选节点对未标记范围内边缘节点的影响，以此来除去节点之间的影响重合范围。下面首先介绍构成ECA算法的评估单个节点影响力、去除边缘节点影响力范围重合两部分，然后整体描述算法的总流程，最后进行实例分析。

3.1 单个影响力节点选取

利用节点影响力最大化算法选取的节点称为种子节点。根据实际需求或成本等的不同，不同应用场景中需要选取的节点数也存在差异。若需要选取网络中的k个种子节点，ECA算法利用以下方式来选取网络中最具信息传播影响力的节点集。

3.1.1 根据k-core算法批量选取

k-core算法通过对网络层次结构的层层分解，评估出节点在整个网络的全局性核心程度，即k-core算法是把网络中节点度小于ks的节点去除的过程。

本文利用节点的k-core数ks值来评估节点的全局结构影响力。从k-core算法可以看出，该算法虽然可以在一定程度上评估出节点在网络中的影响力大小，但仍然不够细分，无法挑选出唯一的影响力最大节点。因此本文在进行节点信息传播影响力评估时，在k-core的基础上进一步考虑节点邻近结构信息。

3.1.2 根据节点邻近结构信息细化选取

结合独立级联模型的特点，评估节点邻近结构影响力Iv-near时，ECA算法考虑了节点v对其邻居的贡献程度以及节点v的集聚系数。v的每一条连边对其邻居节点的贡献度体现了v对其每个邻居节点的影响程度大小，取邻居节点度的倒数即1/di为贡献值；节点集聚系数（clustering coefficient）Cv描述了节点的邻居节点连接的紧密性，v的集聚系数越大，v的邻居节点之间存在的边数ev越大，则当以v为初始传播节点时，信息成功传播给其邻居节点的可能性越大。因此定义节点v的邻近结构影响力如下：

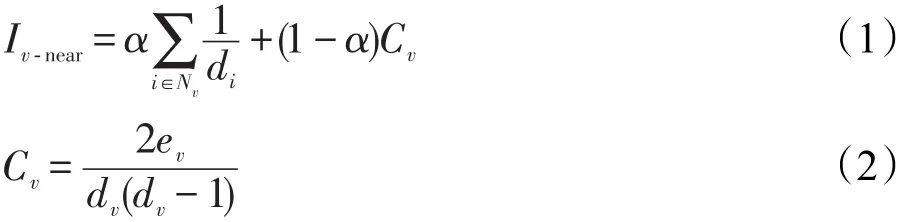
式中，α是权值，根据实验结果调整得出具体值且α＞0.5；Nv是v的邻居节点集，根据图论知识可以推出；dv(dv-1)/2是v的邻居节点组成的全连通图具有的连边数量。通过式（1）计算Iv-near值，选取Iv-near值最大的节点为种子节点。

3.2 去除边缘节点影响范围重合

节点影响范围定义为：利用节点（集）作为信息初始传播节点，信息传播结束后已激活的节点总数。节点影响范围重合是指：通过指定的方法评估出来的具有较大影响力节点的影响区域部分重叠的情况。

影响范围重合出现的原因是种子节点之间存在共邻节点，且任意两个节点i、j影响力重合范围（overlapped range，OR）满足：

由于在独立级联传播模型中，每条边具有传播概率独立的特性，基于独立级联模型的影响力最大化算法在选取种子节点时需要考虑将节点可能影响范围最大化。节点影响力重合问题使节点信息传播影响力不能得到最大的发挥。针对上述问题，覆盖类算法如最大度覆盖、最大核覆盖以及CCA算法均利用标记已选取节点的影响区域的方法来解决。但由于此类算法在选取节点后，并没有考虑已标记区域对未标记区域边缘节点的影响，从而导致后续选取的节点仍然存在边缘影响范围的重合问题。为了更好地阐述边缘节点影响范围重合问题，现做出以下定义。

定义1（边缘贡献）边缘贡献是指在覆盖类影响力最大化算法中，由于已标记区域与未标记区域节点存在连边，从而对这些节点的传播影响力评估产生贡献。

图1表示节点X、Y与已标记区域的连接结构。从图中可以看出，覆盖类算法选取种子节点后将其邻居节点标记为节点影响范围，而已标记区域与未标记区域的边缘节点X仍存在连边，即已标记区域对节点X存在边缘贡献，这就导致了选取后续种子节点时节点影响力评估存在过量估计。在X、Y的节点影响力比较中对边缘节点X更有利，从而导致边缘节点影响范围重合且重合范围满足：

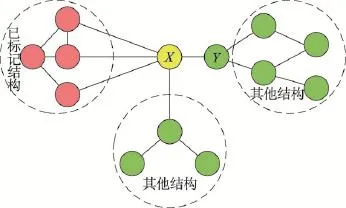
Fig.1 Sketch map of edge node图1 边缘节点示意图

下面通过一个具体的网络W直观分析现有覆盖类影响力算法存在的边缘节点影响范围重合问题。图2展示了W的网络拓扑。

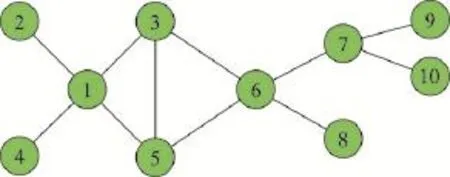
Fig.2 Network topology structure ofW图2 网络W的网络拓扑结构

若需要的种子节点数为2，即k=2，利用CCA算法（d=1）的节点影响力评估方法可以得到以下结果。

不同核数的节点集合分别是：

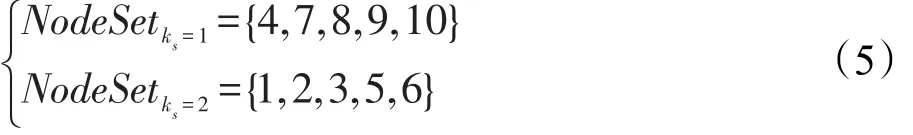
不同度数的节点集合分别是：

综合节点核数与度数选取出的备选种子节点为{1,3,6}。从这里可以看出，最大核覆盖、最大度覆盖、CCA算法的节点影响力评估方式均无法将节点影响力进一步细分。为了后面问题分析更为直观，这里将节点1选为种子节点，则按照现存覆盖类算法的标记方式，将节点1的邻居节点标记。继续根据节点原有核、度属性选取标记区域以外的节点，则下一个种子节点为6，选取结束。

从上述算法种子节点第二轮选取过程中可以看出，由于已标记区域（图3中的红色节点）中节点3、5与未标记区域边缘节点6存在连边，则已标记区域对节点6产生边缘贡献，导致节点1与节点6的影响范围重合且重合范围OR1,6满足：

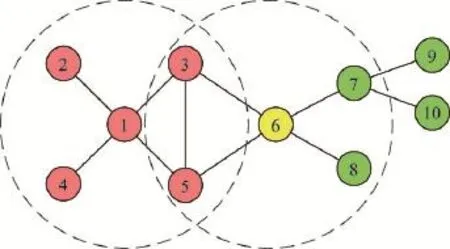
Fig.3 Edge node influence range overlap图3 边缘节点影响范围重合

针对上述边缘节点影响范围重合问题，本文通过去除已标记区域节点及连边，并在下一次循环选取种子节点之前更新网络拓扑结构，最后根据当前网络结构重新计算节点影响力值，以新的节点影响力值大小为标准选取种子节点，以此来达到屏蔽已标记区域对未标记区域边缘产生影响的目的。具体实现流程如下。

对于网络G=(V,E)，当选取第一个种子节点u后，删除种子节点u和邻居节点及其它们所有连边，即：

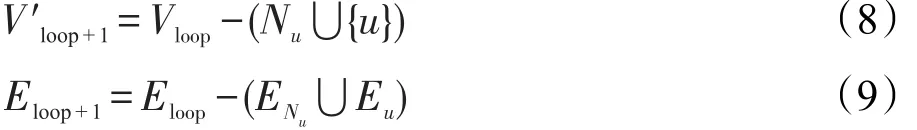
式中，V′loop+1是删除u及u的邻居节点后的网络节点集；Eloop+1是选取下一个种子节点前网络的边集；Eu、分别是u和其邻居的边集。

已标记区域删除后，在下一次循环开始前网络更新为：

式中，Visolated是网络中的孤立节点集；Vloop+1是选取下一个种子节点前网络的节点集。

由于删除已标记区域而出现的孤立节点信息传播影响力极小，不具有被选取为种子节点的可能。因此利用式（10）检测网络中存在的孤立节点集，并将其从当前网络中删除，最后形成全新的连通网络并进入下一次循环。通过上述去重方法，可有效避免边缘贡献带来的节点影响力评估误差，从而解决边缘节点影响力范围重合问题。

3.3 ECA算法总流程

综上所述，结合单个影响力节点选取和去重方案，ECA算法整体详细步骤为：

（1）根据k-core算法选取ks值最大的节点。若出现多个节点ks值相同的情况，则到第（2）步；若结果唯一，则选为种子节点，到第（3）步。

（2）选取Iv-near值最大的节点。若出现多个节点Iv-near值相同的情况，则任意选取其中之一，到第（3）步；若结果唯一，则选为种子节点，到第（3）步。

（3）将选取的种子节点及其邻居节点从网络中删除，同时也删除它们的所有连边。

（4）更新网络拓扑结构。

（5）检测网络中是否存在孤立节点，若存在则删除孤立节点，更新网络结构；若不存在，则到第（6）步。

（6）回到步骤（1）继续选取节点，直到选取k个种子节点为止。

根据上述原理，算法伪代码如下。

算法1 ECA

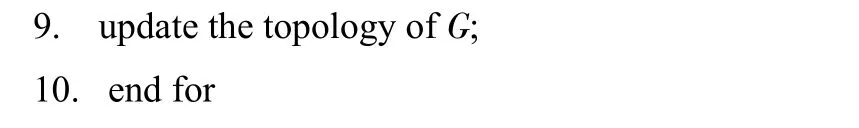
假设网络G=(V,E)有n个节点，m1条边，要选取k个种子节点，ECA算法的复杂度分析如下：首次进行种子节点选取时，利用k-core算法，复杂度为O(m1)；在选取种子节点后，删除相关节点及连边后更新网络，此时网络中有m2条边，再次利用k-core算法，选取下一种子节点，此时复杂度为O(m1+m2)；以此类推，选取第k个种子节点时，网络中的边为mk，复杂度为O(mk-1+mk)。一共需要选取k个节点，因此ECA算法的复杂度为O[m1+(m1+m2)+…+(mk-1+mk)]，即O[2(m1+m2+…+mk)-mk]。相比于CCA算法的复杂度O(km)，该算法的复杂度略高，处于同一个数量级，但其准确度优于CCA算法。相比于贪心算法的复杂度O(kmn)，该算法的复杂度明显优于贪心算法。

4 仿真验证

4.1 实验数据集

为了验证ECA算法的合理性，本文利用IC模型作为传播模型，美国安然公司E-mail网络、DBLP网络结构数据作为算法的仿真网络。E-mail网络是公司员工邮件交流形成的社交网络。DBLP（Digital Bibliography Library Project）网络是论文作者合作网络。ca-HepPh（High Energy Physics-Phenomenology）网络是高能物理现象科学合作作者提交论文的协作网络。3个网络均属于无向网络，且具有明显的无标度特性。网络基本数据如表1所示。

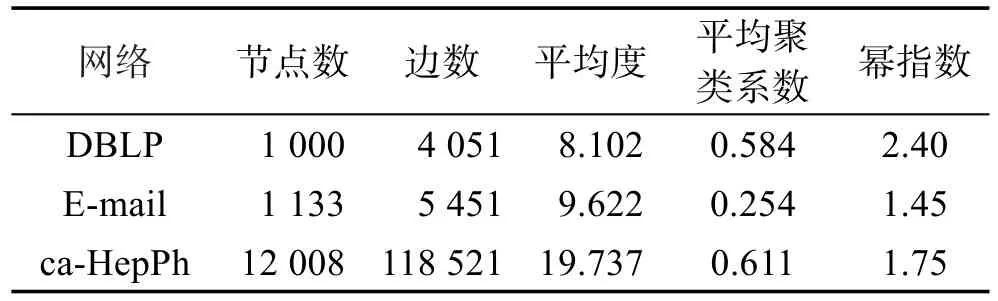
Table 1 Network basic data表1 网络基本数据

4.2 衡量指标

通常情况下，准确度是在给定的传播模型基础上，算法选定的种子节点在传播结束后最终能够影响到的节点数量，即节点影响范围。在社交网络的商品推广等应用领域中，商品信息的传播范围一定程度上代表了推广工作的成功程度，算法准确度越高，节点影响范围越大，则影响到的社交用户越多。因此，准确度是评价影响力最大化算法的重要指标。本文考察种子节点数k从1增加到30传播范围的变化情况，并与其他相关算法进行比较分析。另外，为了更加显著地体现出每种算法效果的差异性，定义：

式中，wk是两种算法在种子节点数为k时的影响范围差异；RECA是ECA算法的节点传播影响范围；RA是算法A的节点传播影响范围；A分别是度启发式（2003年）、k-core启发式（2010年）、最大度覆盖（2010年）、最大核覆盖（2010年）以及CCA算法（2015年）；waverage是差异百分比平均值。每种算法选取1到30个节点分别在IC模型中运行50次，影响范围结果取平均值。

4.3 结果分析

4.3.1 DBLP网络上的结果分析

图4～图8分别展示了传播概率 p取0.01到0.10之间5种不同值时各种算法的影响范围情况，横轴代表种子节点数k，纵轴代表节点影响范围。从图中可以看出：ECA算法在传播概率大于等于0.03时，效果优于其他算法；随着种子节点数增大，不同算法的差别更加明显；随着传播概率的增大，ECA算法的优势更加显著。下面针对不同传播概率下的算法结果走势进行具体分析。

当传播概率为0.01时，由于概率极小，除k-core算法外，其他最大化算法之间的效果差异较小。这种情况下，Degree算法表现出了微弱的优势，这是因为当传播概率极小时，单个节点可能影响到的范围非常有限，节点局部影响力发挥相对重要的作用。此时节点的度数基本决定了影响范围的大小。另外，在种子节点数越大时，k-core算法的表现越差，这是由于k-core算法注重节点全局影响力，并且根据kcore算法选取出的核数最大的节点集通常联系较为紧密，从而节点影响范围存在大面积重合，导致算法结果较差。

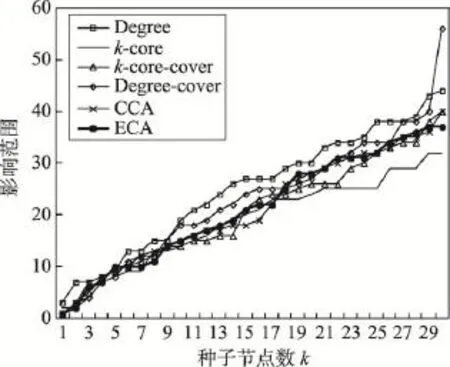
Fig.4 Influence range ofp=0.01in DBLP network图4 DBLP网络中p=0.01时不同算法影响范围

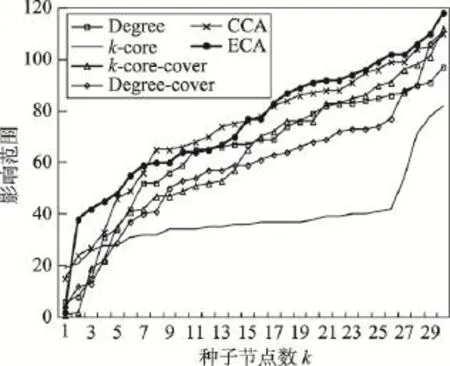
Fig.6 Influence range ofp=0.05in DBLP network图6 DBLP网络中p=0.05时不同算法影响范围

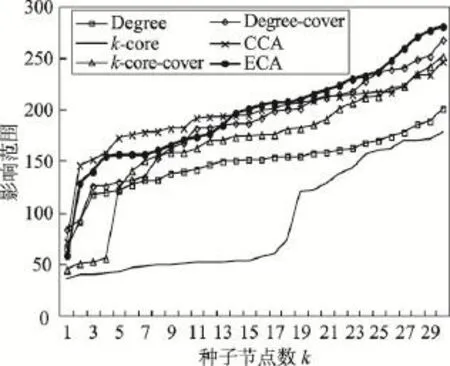
Fig.8 Influence range ofp=0.10in DBLP network图8 DBLP网络中p=0.10时不同算法影响范围

Fig.5 Influence range ofp=0.03in DBLP network图5 DBLP网络中p=0.03时不同算法影响范围

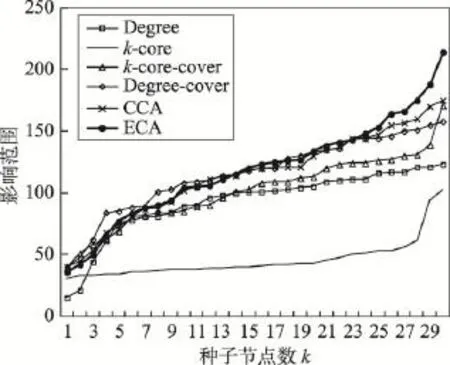
Fig.7 Influence range ofp=0.07in DBLP network图7 DBLP网络中p=0.07时不同算法影响范围

当传播概率为0.03时，虽然各大算法的差距并不算特别明显，但可以看出，Degree算法的效果有了较大幅度下降，基于覆盖类算法ECA、CCA、最大度覆盖、最大核覆盖的效果开始提升。这是因为随着传播概率的增大，节点影响力不再局限于节点局部度数，全局结构信息开始发挥作用。在种子节点数大于24时，ECA算法具有明显的优势。

当传播概率为0.05时，算法之间出现了较为明显的差距，特别是基于k-core的启发式算法效果已经无法和其他算法相提并论，这也体现了节点影响力最大化算法中去除重合范围的重要性。ECA、CCA算法略领先于其他算法，两者差距不明显。

当传播概率为0.07时，ECA、CCA算法的优势已经相当明显。特别是当种子节点数越大时，ECA算法优势极其明显。相对的，Degree算法效果急剧下降，在除了k-core算法的几种算法中，结果最为不理想，说明了随着传播概率的增大，节点影响力范围从邻居节点逐步扩大，因此仅仅考虑节点度数不能恰当评估节点影响力。

当传播概率为0.10时，ECA和CCA算法已经和其他算法存在较大差距。种子节点数较少时，CCA算法表现优异，但当种子节点数增多时，ECA算法表现更为优异且与CCA有明显差距。

表2展示了DBLP网络中ECA算法与其他算法的影响范围平均差异百分比。从表2中可以看出，度启发式算法随着传播概率的增大算法效果下降趋势最为明显，k-core启发式算法效果最差，CCA算法在5种对比算法中最优，而本文算法ECA比CCA算法更有优势。整体来说，ECA算法在传播概率大于0.03时优势明显，并且随着k值增加，ECA算法的优化效果更加显著。这是因为ECA算法在去除影响范围重合时考虑了未标记区域边缘节点影响范围的重合问题。因此，相比其他算法而言，选取的节点数越多，ECA算法在去重方面更具有优势，最后的优化结果也更为明显。

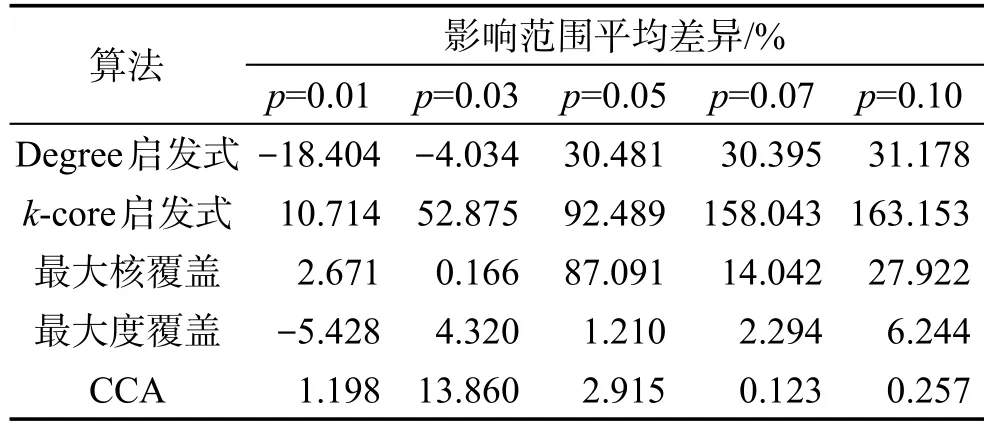
Table 2 Mean difference of influence range of ECA algorithm and other algorithms in DBLP network表2 DBLP网络中ECA算法与其他算法影响范围平均差异

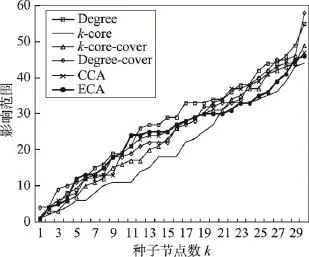
Fig.9 Influence range ofp=0.01in E-mail network图9 E-mail网络中p=0.01时不同算法影响范围

4.3.2 E-mail网络上的结果分析

图9～图13分别展示了传播概率取0.01到0.10之间5种不同值时各种算法的影响范围情况。从图中可以看出：ECA算法在传播概率大于等于0.05时，效果优于其他算法；随着种子节点数k增大，ECA算法的优势更加显著。

从前面DBLP网络的结果分析可知，当传播概率为0.01时，由于传播概率极小，信息很难在网络中扩散，导致各种算法的影响范围较为接近。

传播概率为0.03时，Degree算法具有相当的优势，除了k-core算法，其他算法的差距较小。从E-mail网络和DBLP网络的基本数据可以看出，DBLP网络的平均集聚系数是E-mail网络的2.3倍左右。经过仿真运算，在DBLP网络中，节点核数最大为23，相同核数的节点数量为322；在E-mail网络中，节点核数最大为11，共有66个节点。从这些数据可以看出，E-mail网络结构更为疏松，因此度中心性在节点信息传播影响力中发挥了非常重要的作用，这也是Degree算法在E-mail网络比DBLP网络表现更为优越的原因。

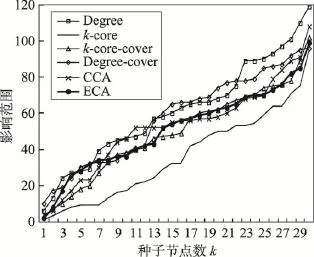
Fig.10 Influence range ofp=0.03in E-mail network图10 E-mail网络中p=0.03时不同算法影响范围

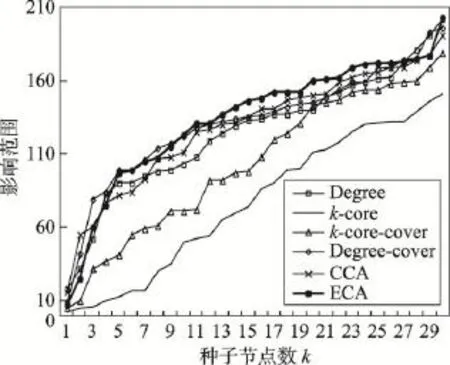
Fig.11 Influence range ofp=0.05in E-mail network图11 E-mail网络中p=0.05时不同算法影响范围

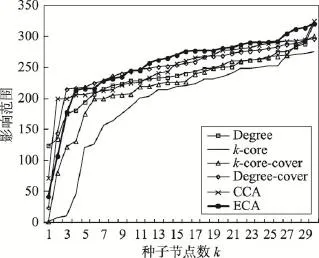
Fig.12 Influence range ofp=0.07in E-mail network图12 E-mail网络中p=0.07时不同算法影响范围

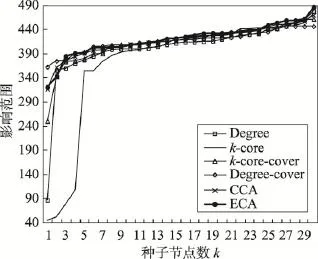
Fig.13 Influence range ofp=0.10in E-mail network图13 E-mail网络中p=0.10时不同算法影响范围

随着传播概率增大到0.05，以Degree算法为代表的通过局部影响力来评估节点影响力的方法结果开始变差，基于影响力覆盖的算法开始发挥优势，ECA、CCA算法目前效果较优。

传播概率为0.07时，ECA算法仍然存在优势，而Degree算法效果持续下降，但k-core算法和其他算法的差距却逐渐缩小，比起DBLP网络中k-core算法极差的表现，在E-mail网络中其效果较好。出现这种现象的原因是对于拓扑结构越疏松的网络，利用k-core算法选取的节点影响力重合范围越小，因此算法效果比平均集聚系数大的网络较优。

当传播概率为0.10时，ECA较其他算法存在一定优势，效果优化程度由大到小为ECA＞CCA＞最大度覆盖＞最大核覆盖＞Degree＞k-core。

表3展示了E-mail网络中ECA算法与其他算法的影响范围平均差异百分比，从表中可以更为清晰地看出，ECA算法在基于k-core的最大化算法中具有较大的优势，而Degree启发式的效果随着传播概率增大明显变差。

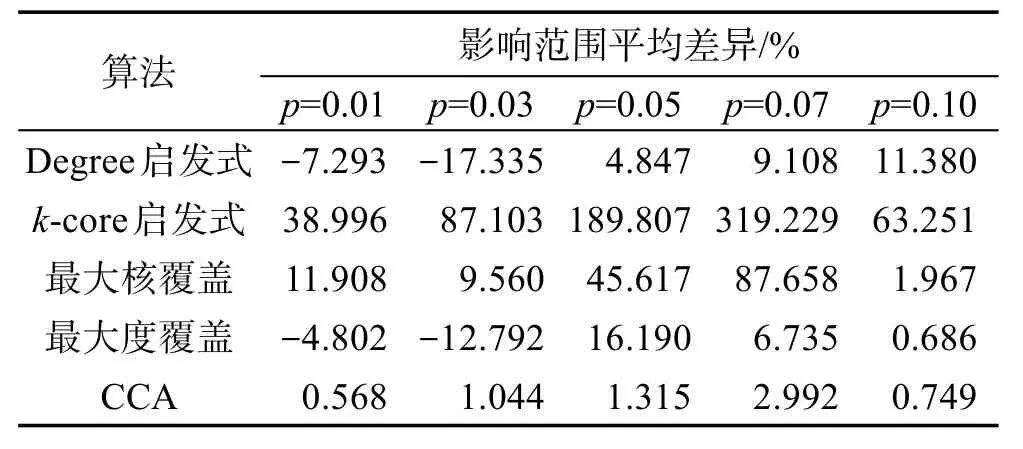
Table 3 Mean difference of influence range of ECA algorithm and other algorithms in E-mail network表3 E-mail网络中ECA算法与其他算法影响范围平均差异

4.3.3 ca-HepPh网络上的结果分析

图14～图18分别展示了传播概率取0.01到0.10之间的5种不同值时各种算法的影响范围情况。从图中可以看出：ECA算法在传播概率大于等于0.01时，效果优于其他算法；随着种子节点数k和传播概率的增大，ECA算法优势更加明显。下面是针对不同传播概率下的算法结果的具体分析。

从前面两个网络的结果分析可知，当传播概率取0.01时，传播概率极小，信息在网络中进行传播较为困难，因此各种算法之间的效果差异较小。

当传播概率为0.03时，各个算法的差距不大，随着种子节点数量的增加，ECA算法的优势越来越明显。

在传播概率大于0.05时，基于影响力覆盖的ECA算法与CCA算法优势明显，并且随着种子节点数量的增加及传播概率的增大，ECA算法优势更为明显。而仅考虑局部影响力评估节点影响力的Degree算法等效果较差。

表4展示了ca-HepPh网络中ECA算法与其他算法的影响范围平均差异百分比。整体来说，ECA算法在传播概率大于0.03时优势明显，并且随着k值增加，ECA算法的优势更加显著。

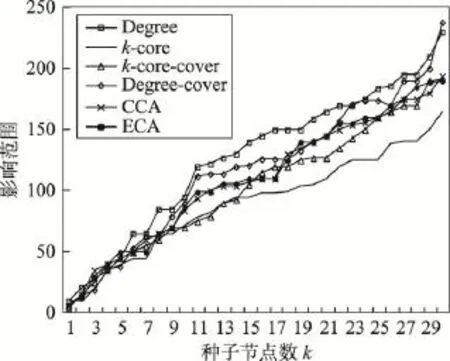
Fig.14 Influence range ofp=0.01in ca-HepPh network图14 ca-HepPh网络中p=0.01时不同算法影响范围

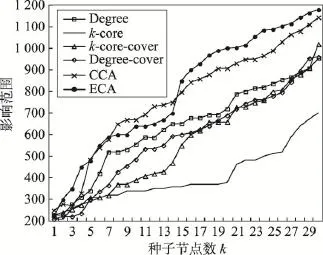
Fig.16 Influence range ofp=0.05in ca-HepPh network图16 ca-HepPh网络中p=0.05时不同算法影响范围

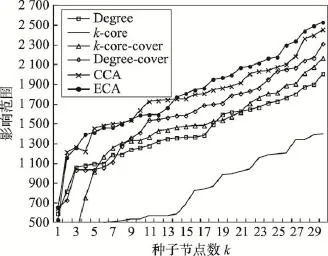
Fig.18 Influence range ofp=0.10in ca-HepPh network图18 ca-HepPh网络中p=0.10时不同算法影响范围

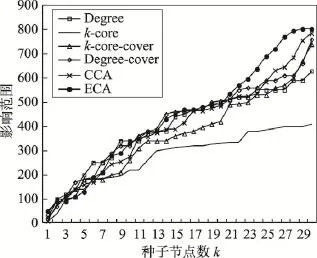
Fig.15 Influence range ofp=0.03in ca-HepPh network图15 ca-HepPh网络中p=0.03时不同算法影响范围

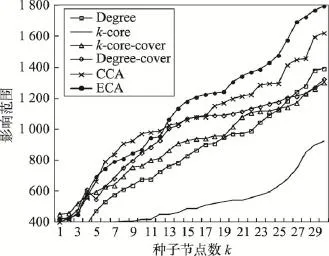
Fig.17 Influence range ofp=0.07in ca-HepPh network图17 ca-HepPh网络中p=0.07时不同算法影响范围

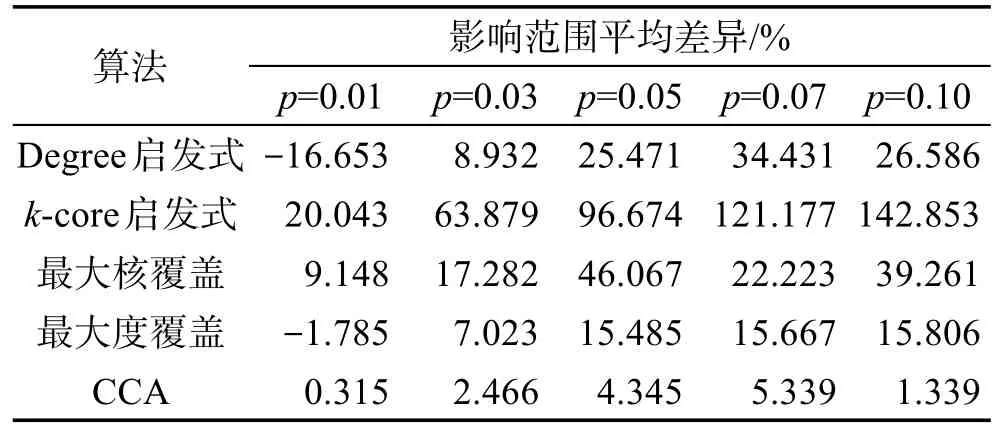
Table 4 Mean difference of influence range of ECA algorithm and other algorithms in ca-HepPh network表4 ca-HepPh网络中ECA算法与其他算法影响范围平均差异

在同等的硬件坏境下，DBLP网络和E-mail网络中Degree启发式和最大度覆盖的运行时间平均在2 s以下，k-core启发式、最大核覆盖以及CCA算法的运行时间在37 s左右，ECA算法为80 s左右。在数据规模较大的ca-HepPh网络中，Degree启发式和最大度覆盖的运行时间在100 s以下，k-core启发式、最大核覆盖以及CCA算法的运行时间在4 000 s左右，ECA算法为7 000 s左右。Degree启发式算法运行时间较短，但其效果最差。相较于其他算法中效果最好的是CCA算法，ECA算法运行时间略长，但是ECA算法的准确度优于其他算法，其运行时间在可被接受的范围内，可以看出ECA算法整体效果较优。

通过在3种网络中的影响范围结果比较可以看出，种子节点越多、网络规模越大时，ECA算法的效果越好。此外，p从0.01到0.10，DBLP网络中节点影响力最大范围依次为56，80，118，214，281；E-mail网络中节点影响力最大范围依次为58，119，203，325，487。在相同的传播概率条件下，两者差距极其明显，E-mail网络的最大范围比DBLP网络更大。由此可以得出结论，在相同初始条件下，集聚系数越大的网络信息传播范围越小。

5 结束语

影响力最大化问题是社会网络信息传播研究中的关键问题之一，目的是发现网络中最具有传播影响力的节点，在广告发布、舆情控制、市场营销等许多重要场景中都有广泛的应用。本文提出了基于IC模型的节点影响力最大化算法ECA，结合k-core算法及节点邻近结构信息来评估节点影响力，并通过去除已选节点影响范围的方式来屏蔽已选区域对边缘节点的影响，以此来除去节点之间的影响重合范围。仿真结果证明ECA算法能够增大节点信息传播影响范围，比其他算法效果更优。

在后续研究工作中，考虑将网络结构基本数据分析与节点影响力最大化问题联系起来，根据网络实际情况和初始传播节点数量需求不同，实现算法中节点影响力评估方法的自适应调整，从而在影响传播范围以及运行时间优化方面提高影响力最大化算法的性能，进而拓展影响力最大化算法应用领域。

[1]Domingos P,Richardson M.Mining the network value of customers[C]//Proceedings of the 7th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco,USA,Aug 26-29,2001.New York ACM,2001: 57-66.

[2]Kempe D,Kleinberg J,Tardos É.Maximizing the spread of influence through a social network[C]//Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Washington,Aug 24-27, 2003.New York:ACM,2003:137-146.

[3]Leskovec J,Krause A,Guestrin C,et al.Cost-effective outbreak detection in networks[C]//Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,San Jose,USA,Aug 12-15,2007.New York:ACM,2007:420-429.

[4]Goyal A,Lu Wei,Lakshmanan L V S.CELF++:optimizing the greedy algorithm for influence maximization in social networks[C]//Proceedings of the 20th International World Wide Web Conference,Hyderabad,India,Mar 28-Apr 1, 2011.New York:ACM,2011:47-48.

[5]Chen Wei,Wang Yajun,Yang Siyu.Efficient influence maximization in social networks[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Paris,Jun 28-Jul 1,2009.New York:ACM,2009:199-208.

[6]Liu Xiaodong.Research on efficient processing techniques of influence maximization in large-scale socialnetworks[D]. Changsha:National University of Defense Technology,2013.

[7]Tian Jiatang,Wang Yitong,Feng Xiaojun.A new hybrid algorithm for influence maximization in social networks[J]. Chinese Journal of Computers,2011,34(10):1956-1965.

[8]Chen Hao,Wang Yitong.Threshold-based heuristic algorithm for influence maximization[J].Journal of Computer Research and Development,2012,49(10):2181-2188.

[9]Guo Jingfeng,Lv Jiaguo.Influence maximization based on information preference[J].Journal of Computer Research and Development,2015,52(2):533-541.

[10]Guo Jing,Cao Yanan,Zhou Chuan,et al.Influence weights learning under linear threshold model in social networks[J]. Journal of Electronics and Information Technology,2014, 36(8):1804-1809.

[11]Zhang Bolei,Qian Zhuzhong,Wang Qinhui,et al.Maximize information coverage algorithm for target marke[J]. Chinese Journal of Computers,2014,37(4):894-904.

[12]Chen Wei,Wang Chi,Wang Yajun.Scalable influence maximization for prevalent viral marketing in large-scale social networks[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Washington,Jul 25-28,2010.New York:ACM,2010: 1029-1038.

[13]Chen Wei,Yuan Yifei,Zhang Li.Scalable influence maximization in social networks under the linear threshold model[C]//Proceedings of the 10th International Conference on Data Mining,Sydney,Dec 13-17,2010.Washington:IEEE Computer Society,2010:88-97.

[14]Jung K,Heo W,Chen Wei.IRIE:a scalable influence maximization algorithm for independent cascade model and its extensions[J].arXiv:1111.4795,2011.

[15]Kitsak M,Gallos L K,Havlin S,et al.Identification of influential spreaders in complex networks[J].Nature Physics, 2010,6(11):888-893.

[16]Goyal A,Lu Wei,Lakshmanan L V S.SIMPATH:an efficient algorithm for influence maximization under the linear threshold model[C]//Proceedings of the 11th International Conference on Data Mining,Vancouver,Canada,Dec 11-14, 2011.Washington:IEEE Computer Society,2011:211-220.

[17]Cao Jiuxin,Dong Dan,Xu Shun,et al.A k-core based algorithm for influence maximization in social networks[J].Chinese Journal of Computers,2015,38(2):238-248.

附中文参考文献：

[6]刘晓东.大规模社会网络中影响最大化问题高效处理技术研究[D].长沙:国防科学技术大学,2013.

[7]田家堂,王轶彤,冯小军.一种新型的社会网络影响最大化算法[J].计算机学报,2011,34(10):1956-1965.

[8]陈浩,王轶彤.基于阈值的社交网络影响力最大化算法[J].计算机研究与发展,2012,49(10):2181-2188.

[9]郭景峰,吕加国.基于信息偏好的影响最大化算法研究[J].计算机研究与发展,2015,52(2):533-541.

[10]郭静,曹亚男,周川,等.基于线性阈值模型的影响力传播权重学习[J].电子与信息学报,2014,36(8):1804-1809.

[11]张伯雷,钱柱中,王钦辉,等.面向目标市场的信息最大覆盖算法[J].计算机学报,2014,37(4):894-904.

[17]曹玖新,董丹,徐顺,等.一种基于k-核的社会网络影响最大化算法[J].计算机学报,2015,38(2):238-248.

HU Min was born in 1971.She received the M.S.degree from Chongqing University of Posts and Telecommunications in 2002.Now she is an associate professor and M.S.supervisor at School of Communication and Information Engineering,Chongqing University of Posts and Telecommunications.Her research interests include wireless communication,communication network system and protocol etc.

胡敏（1971—），女，重庆人，2002年于重庆邮电大学获得硕士学位，现为重庆邮电大学通信与信息工程学院副教授、硕士生导师，主要研究领域为无线通信通信，网体系与协议等。

SUN Xinran was born in 1991.She is an M.S.candidate at School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications.Her research interest is communication network.

孙欣然（1991—），女，河北石家庄人，重庆邮电大学通信与信息工程学院硕士研究生，主要研究领域为通信网络。

HUANG Hongcheng was born in 1979.He received the M.S.degree in communication and information engineering from Chongqing University of Posts and Telecommunications in 2006.Now he is an associate professor at School of Communication and Information Engineering,Chongqing University of Posts and Telecommunications,and the member of CCF.His research interests include ad hoc network and delay tolerant network,etc.

黄宏程（1979—），男，河南南阳人，2006年于重庆邮电大学通信与信息工程专业获得硕士学位，现为重庆邮电大学通信与信息工程学院副教授，CCF会员，主要研究领域为无线自组织网络，容迟网络等。

Edge-CoverAlgorithm for Influence Maximization in Social Network*

HU Min1,SUN Xinran1,HUANG Hongcheng1,2+
1.School of Communication and Information Engineering,Chongqing University of Posts and Telecommunications, Chongqing 400065,China
2.College of Computer Science,Chongqing University,Chongqing 400044,China

+Corresponding author:E-mail:huanghc@cqupt.edu.cn

HU Min,SUN Xinran,HUANG Hongcheng.Edge-cover algorithm for influence maximization in social network.Journal of Frontiers of Computer Science and Technology,2017,11(5)：720-731.

Influence maximization is a problem of obtaining a subset of nodes in social network to maximize the influence spread.Aiming at the problem of the poor accuracy of heuristic algorithm,existing works consider the overlapped range,and ignore the problem of edge contributions.This paper focuses on how to select a seed set that has the maximum influence based on edge contributions.The algorithm evaluates the influence of information spread by calculating the global influence and adjacent influence.Then it removes the selected node influence range and updates the network to eliminate the interference of edge contributions to node influence evaluation.Finally,this paper proposes an edge-cover algorithm for influence maximization based on independent cascade model.The experimental results show that the proposed algorithm has a greater impact on the spread of range.

social network;influence maximization;edge contributions;heuristic algorithm

10.3778/j.issn.1673-9418.1605063

A

：TP391.9

*The National Natural Science Foundation of China under Grant No.61401051(国家自然科学基金);the Foundation and Frontier Research Project of Chongqing Science and Technology Commission under Grant No.cstc2014jcyjA40039(重庆市科委基础和前沿研究项目);the Science and Technology Research Project of Chongqing Municipal Education Committee under Grant No.KJ1400402 (重庆市教委科学技术研究项目).

Received 2016-05,Accepted 2016-07.

CNKI网络优先出版:2016-07-14,http://www.cnki.net/kcms/detail/11.5602.TP.20160714.1616.012.html

摘 要：影响力最大化问题是在社交网络中寻找具有最大影响范围的节点集。针对启发式算法准确度相对较差的问题，现有的研究考虑了影响范围重合，但忽略了边缘贡献导致的节点影响力过量评估。重点研究了在考虑边缘贡献的情况下，如何选取影响范围最大的节点集合。采用启发式算法的思想，首先计算节点全局和邻近影响力来评估节点信息传播影响力，通过去除已选节点影响范围并更新网络的方式，消除边缘贡献对节点影响力评估的干扰，在独立级联模型基础上提出了基于边缘去重的节点影响力最大化算法。仿真结果表明所提出算法相比其他算法，能够有效增大节点信息传播影响范围。