标记分布学习中目标函数的选择*
赵 权,耿 新+
1.东南大学 计算机网络和信息集成教育部重点实验室,南京 211189
2.东南大学 计算机科学与工程学院,南京 211189
标记分布学习中目标函数的选择*
赵 权1,2,耿 新1,2+
1.东南大学 计算机网络和信息集成教育部重点实验室,南京 211189
2.东南大学 计算机科学与工程学院,南京 211189
标记分布学习;最大熵模型;拟牛顿法;目标函数选择
1 引言
标记多义性问题是目前机器学习和数据挖掘领域的热门研究方向。目前已有两种比较成熟的学习范式,分别是单标记学习(single-label learning)和多标记学习[1]multi-label learning)。多标记学习是对单标记学习的拓展。通过大量的研究和实验[2-8]表明,多标记学习是一种有效且应用场景广泛的学习范式。
多标记学习仍有可以拓展的地方。多标记学习虽然对于一个示例允许标上多个标记,拓展了单标记学习,但是仍有一些问题是不太适合用多标记学习解决的。例如,后面的实验中提到的人类基因数据集,这个数据中每个基因示例上不是若干个标记,而是一个标记分布。一个标记分布中每个标记通过一个0到1之间的值表示对示例的描述程度。对于这类数据集,不仅希望预测新示例的正确标记,还希望预测每一个标记对示例的描述程度。多标记学习不容易直接求解这类问题。因此,为了解决这类问题,Geng等人[9]拓展了多标记学习,提出了标记分布学习(label distribution learning)范式。与多标记学习输出一个标记集合不同,标记分布学习输出的是一个标记分布,分布中的每个分量表示对应标记对示例的描述程度。标记分布学习是一种适用场景更广的学习范式,能够解决更多的标记多义性问题。相关的研究成果[9-15]也说明了这一点。
目前,已有一些标记分布学习算法[9-15]被提出来。这些算法的设计策略主要分为以下3类:(1)将标记分布学习问题转换为单标记学习等问题进行求解。(2)对现有的算法(例如k近邻、神经网络等算法)进行调整和拓展以解决标记分布学习问题。(3)直接匹配标记分布学习,设计专门的算法。相关的研究成果[9]表明,在这3种策略中,第三种直接针对标记分布学习设计专门算法的策略是效果最好的。基于这一点,对第三种策略进行分析,泛化出一种框架,并对泛化框架中的某些组成部分进行深入研究,将有可能提升用第三种策略设计出的标记分布学习算法的效果。因此,本文提出一种泛化框架,并着重研究框架中的目标函数部分对算法预测效果的影响。
本文的主要贡献有以下几点:首先针对较为有效的标记分布学习算法设计策略,泛化出一种算法设计框架。其次,根据标记分布学习的特点,选取若干较具代表性的距离(度量两个分布间的不相似程度的函数)进行研究。基于5个真实标记分布数据集的实验结果,本文分析了选取不同距离作为泛化框架中的目标函数对算法预测效果的影响。最后,提出了若干选择目标函数的建议。
本文组织结构如下:第2章简要介绍标记分布学习。第3章针对上述提到的第三种标记分布算法设计策略,泛化出一种算法设计框架,然后根据一定的策略选取若干具有代表性的距离,并使用这些距离特化出若干个标记分布学习算法。第4章在5个真实的标记分布数据集上进行实验,比较这些特化算法的预测效果;基于实验结果,分析选择不同距离作为目标函数对特化算法预测效果的影响,并给出相应的结论和建议。第5章总结全文。
2 标记分布学习
标记分布学习是对多标记学习的拓展。在多标记学习中,对于一个新示例,会输出一个预测标记集合。因此,对于一个标记,多标记学习的输出只有0(表示不是正确标记)和1(表示是正确标记)两种结果。假设共有n个标记,则多标记学习不同的输出总数是2n-1个,而单标记学习的输出总数是n个。单从输出总数上就可以直观地发现多标记学习对示例具有更丰富的标记表示。图1形象地说明了这一点。图1表示的是在只有两个标记情况下的典型学习问题中,3种学习范式的特征空间决策域。其中,单标记学习可能的标记表示只有两种,红色色块对应标记1的决策域,黄色则对应标记2。而多标记学习则有3种,除了单标记学习输出的两种表示外,还有同时输出标记1和标记2(中间的橙色色块)。标记分布学习的标记表示则有无穷多种,图1中每一个点都代表一个标记分布的决策域。直观上这是一种从离散值表示到连续值表示的拓展。标记分布学习不再是输出一个标记的集合,而是输出一个标记分布。下面将正式给出这种输出的形式化表示。
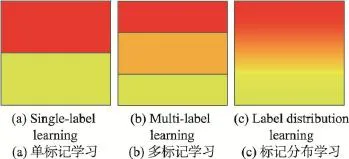
Fig.1 Decision regions of 3 learning paradigms for a learning problem with two labels图1 两标记的学习问题中3种学习范式的特征空间决策域
对于数据集中的第i个示例,用xi来表示。第i个示例对应的标记分布,用Di来表示。Di可以表示为,其中n表示一共有n个标记。表示第 j个标记对示例i的描述程度(简称描述度),其值为0到1之间的实数,值越大,表示越能描述第i个示例,并且满足,表示所有标记共同完备地描述一个示例。
单标记学习和多标记学习都可以看成是标记分布学习的特例。如图2所示,对于单标记学习,可以通过将示例的真实标记的描述度设为1,而其他标记的描述度设为0的方式,将单标记输出转换为标记分布输出。同样的,在多标记学习中,假设一个示例有两个正确的标记,可以将这两个标记的描述度都设为0.5,其他标记的描述度设为0。这样就可以把标记集合转换为标记分布了。通过上述方式可以将单标记学习和多标记学习问题都转换为标记分布学习问题。这说明标记分布学习的泛化程度更高,具有更多的适用场景。
3 泛化标记分布学习框架
3.1 基于专门算法设计策略的泛化框架
目前针对标记分布学习,设计算法的策略主要有以下3种:
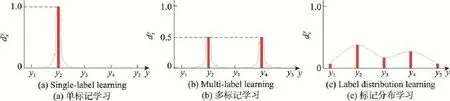
Fig.2 Label distribution of 3 learning paradigms图2 3种学习范式对应的标记分布
第一种策略是问题转换。这种策略首先将标记分布学习问题转换为单标记学习等问题后,再利用相应范式中已有的算法进行求解,然后将输出结果转换为标记分布。例如:PT-SVM(problem transformation support vector machine)算法[9]就是先通过重采样,将标记分布数据集转换为单标记数据集;然后在单标记数据集上训练单标记支持向量机(support vector machine,SVM)分类器;最后将分类器输出的结果转换为标记分布。显然这类算法并不是直接求解标记分布学习问题,而是将问题转换为其他范式的学习问题后再求解,求解后还需要将其他范式的输出转换为标记分布。两次转换过程有可能丢失部分原来标记分布中包含的信息。例如:在重采样过程中,以标记的描述度为权重进行采样。描述度越高的标记,在采样后得到的单标记示例越多。对于一些描述度较低的标记,会采样到比较少的单标记示例,甚至有可能没有训练示例出现在单标记训练集中,这就丢失了标记分布的部分信息。同时这种非直接的算法把一个标记分布整体分拆成多个单标记问题求解,忽略了标记之间的相关关系,这可能导致算法的效果不理想。
第二种设计策略是算法调整。这种设计策略没有将标记分布学习问题转换成其他学习范式问题后再进行求解,而是首先寻找一些可以解决多变量回归问题的算法,然后对这些算法进行调整来解决标记分布学习问题。例如:LDSVR(label distribution support vector regressor)算法[15]就是先将标记分布数据集当成多变量回归数据集来训练支持向量机得到一个多变量回归器,再将这个回归器的输出调整为一个标记分布。这种设计策略虽然没有问题转换的过程,不会出现信息丢失和忽略标记间相关性的问题,但是这种设计策略仍存在导致算法效果不佳的因素。多变量回归和标记分布学习本质上还是有区别的。标记分布本质上是一个描述度分布,所有标记对示例的描述具有完备性,也就是说所有标记的描述度的和为1,且每个标记描述度的值为0到1之间。显然,一个标记分布可以认为是一个多变量,但是一个多变量不一定就是一个分布。有一些多变量回归相关的算法是不能保证输出一个分布的,例如LDSVR算法的输出就不一定是一个分布,需要对输出进行调整后转换为一个分布。这个调整过程就有可能影响算法的效果。
第三种策略是针对标记分布学习设计专门的算法。这种策略没有问题转换过程,直接求解标记分布学习问题。而且和第二种策略不同,使用第三种策略设计的算法的输出模型可以直接输出标记分布。因此,这种直接设计专门算法的策略,不存在问题转换过程中的信息丢失问题和对输出结果进行转换导致算法效果受影响的问题。相关研究[9]也表明,用第三种策略设计的算法效果要好于第一、第二种策略设计的算法。因此本文将针对第三种算法设计策略,提出一种泛化标记分布学习算法设计框架,并对框架中的目标函数部分做深入研究,以分析选择不同距离作为目标函数对算法预测效果的影响。
针对第三种算法设计策略可以泛化出一种标记分布学习算法设计框架。仔细分析第三种算法设计策略,发现以这种策略设计的算法由输出模型、优化方法和目标函数三部分组成。因此,本文提出的泛化框架也主要由这三部分组成。这里的输出模型指的是能够直接输出标记分布的输出模型,而不像LDSVR算法那样还要对算法的原始输出做调整才能得到标记分布。用第三种策略设计的算法都可以统一到这个泛化框架中,只不过对应的泛化框架中的三部分不相同。以IIS-LLD和BFGS-LLD算法[9]为例,虽然是两种不同的算法,但是都可以统一到本文所提的泛化标记分布学习框架中。这两种算法在框架中使用的输出模型都是最大熵模型(maximum entropy model)[16],使用的目标函数都是Kullback Leibler散度。不同的是优化方法,IIS-LLD算法使用的优化方法是改进的迭代尺度法(improved iterative scaling,IIS)[17],而BFGS-LLD算法使用的优化方法是拟牛顿法中的BFGS算法[18]。在这个泛化标记分布学习框架中,通过组合不同的输出模型、目标函数及优化方法可以设计出不同的标记分布学习算法。对框架中三部分的改进都有可能提升算法的效果。
已有的研究在设计算法时都主要关注输出模型和优化方法的选择和设计,关于目标函数的研究则相对少些。但是作为框架中的重要组成部分,对目标函数选择方法的改进也能提升算法效果。在使用泛化标记分布学习框架设计算法时,如何选择目标函数的距离是一个十分有价值的问题。因此,基于这个动机,本文将主要关注用不同距离作为目标函数对算法预测效果的影响。
3.2 代表性距离的选取
在泛化标记分布学习框架中,输出模型的输出是一个标记分布,数据集中每个示例对应的也是一个标记分布。因此,标记分布学习中的目标函数必须是能够度量两个分布间不相似程度的距离或相似度。
为了表述方便,本文将距离和相似度统称为距离。可以用来度量两个分布间不相似程度的距离有很多,文献[19]对41种距离进行了语法和语义上的系统研究。本文基于这些系统研究的结果,将选取若干具有代表性的距离作为泛化标记分布学习框架中的目标函数。为了分析41个距离间的相关性,文献[19]使用agglomerative single linkage clustering算法[20]进行了30次独立的相关性分析实验,最终得到的结果如图3所示。图3中横坐标表示两个距离间的相关程度,数值越大表示越不相关。纵坐标则代表不同的距离。横坐标对应的不同树状图分支表示的是用对应的横坐标数值做聚类分析后得到的不同聚类类别。例如:用0.40这个数值进行聚类分析后,可以将所有距离分成两个类别,反映到图3中,就是对应的两个树状图分支。逐渐减小横坐标的数值继续进行聚类分析,可以对树状图的分支进行不断的细分,最后便得到了距离相关性聚类树状图(如图3)。
图3中的每个树状图分支都可以认为是一个距离类别,横坐标数值取得越小,划分得越精细,反之则越粗糙。因此,为了尽可能全面地研究用不同距离作为目标函数对标记分布学习算法预测效果的影响,如图3所示,在横坐标较小值0.05处做横坐标的垂直线,将距离划分为12个类别,并在每个类别中选取一个距离作为这个类别的代表。
在选取距离时,本文会按照以下准则剔除掉一些不合适的距离。(1)当预测分布和真实分布完全一致时,所选距离的计算结果必须达到最小值(相似度则达到最大值),如果不满足则剔除。例如:图3的2号分支中的Inner Product在计算两个相同分布的相似度值时就不一定能达到最大值,因此在选择代表性距离时就剔除它。(2)距离的表达式还必须是连续的,如果不连续则剔除。例如:3号分支中的Chebyshev就不是连续的,选择时也剔除这个距离。(3)在距离的公式中不允许出现除于0的情况,由于本文使用的标记分布输出模型是最大熵模型,这种输出模型不会输出值为0的分量。在执行这条准则时,只需考虑示例的真实分布中有值为0的分量存在的情况。按照这条准则,第4、9及11号分支都被剔除。执行上述准则剔除掉部分距离后,还剩7个分支。需要在这7个分支中分别选出7个代表性距离。
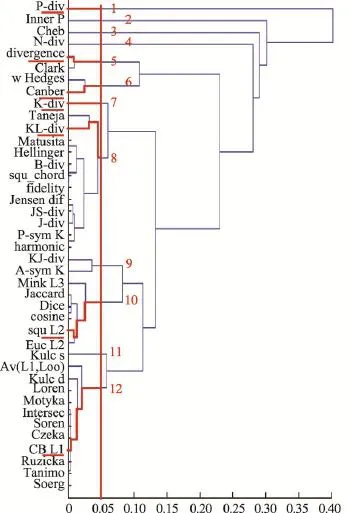
Fig.3 Selected typical distances and cluster hierarchical tree of different distances图3 距离相关性聚类树状图和所选取的代表性距离
在7个分支中选择代表性距离时,如果分支中的距离只有一个,则直接选取。如果有多个,则先按照上面提到的3个准则剔除掉部分不合适的距离后,再通过以下过程选取代表距离。首先某些距离在度量两个分布的不相似程度时是线性等价的。例如:12号分支中的Sørensen和City block,这两个距离在度量两个分布的不相似程度时,通过Sørensen距离公式计算得到的值相当于通过City block距离公式计算得到的值乘上0.5。对于这种情况,本文选择形式最简单的距离代表这一类线性等价的距离。接着,如果还是存在不止一个距离,则选择比较常用和经典的距离作为代表。例如:8号分支中的Kullback Leibler散度。通过上述过程,如图3所示,本文最后选出了7个代表距离。表1给出了这7个距离的名称和形式。在表1中示例的真实标记分布用D={d1,d2,…,dc}表示,输出模型输出的预测标记分布用表示。

Table 1 Name and calculation formula of 7 typical distances表1 7个代表性距离的名称和计算公式
3.3 模型和优化方法
本文接下来将介绍实验中使用的标记分布输出模型和优化方法。由于本文主要关注的是泛化标记分布学习框架中的目标函数部分,为了排除选择不同输出模型和优化方法造成的干扰,实验部分将使用相同的输出模型和优化方法。
实验部分使用的标记分布输出模型是最大熵模型[9,16]。假设一个示例的特征向量用x表示,则最大熵模型输出的第i个标记的预测描述度可以表示为如下形式:
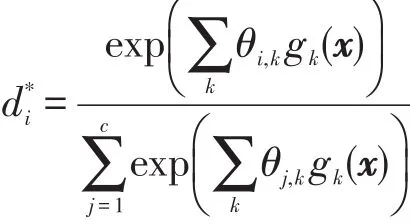
其中,c表示一共有c个标记;θj,k是需要学习的模型参数,和第 j个标记及示例特征向量的第k个分量相对应,假设特征向量有K维,则共有c×K个模型参数;gk(x)表示的是特征向量的第k个分量。
实验部分使用的优化方法是拟牛顿法中的BFGS算法[18]。用牛顿法进行优化时,需要求目标函数的二阶导数矩阵Hessian矩阵的逆矩阵。这个过程不仅是一个计算十分耗时的过程,而且不一定能保证Hessian矩阵是可逆的。拟牛顿法为了解决这个问题,对Hessian矩阵的逆矩阵进行了近似,不同的近似方法得到不同的拟牛顿法,BFGS算法便是其中的一种拟牛顿法。文献[9]给出了BFGS的近似方法和优化过程。对于Canberra和City block距离中不可导的点,使用次梯度作为替代进行梯度下降[21]。
4 实验
4.1 算法预测效果评价指标
为了研究评价指标和目标函数间的关系,本文将7个代表性距离同时作为目标函数和特化算法预测效果的评价指标。文献[19]把41个距离按照其计算公式的语法特点分成了8个语义家族。观察7个代表距离所属的家族,可以发现它们来自4个不同的语法家族。因此,无论在不相关性方面,还是在语法特点方面,这7个距离都具有一定的多样性和广泛的代表性,能在一定程度上从不同方面评价一个特化算法预测效果的好坏。
4.2 数据集
本文在5个真实标记分布数据集上进行实验,表2给出了这些数据集的基本信息。
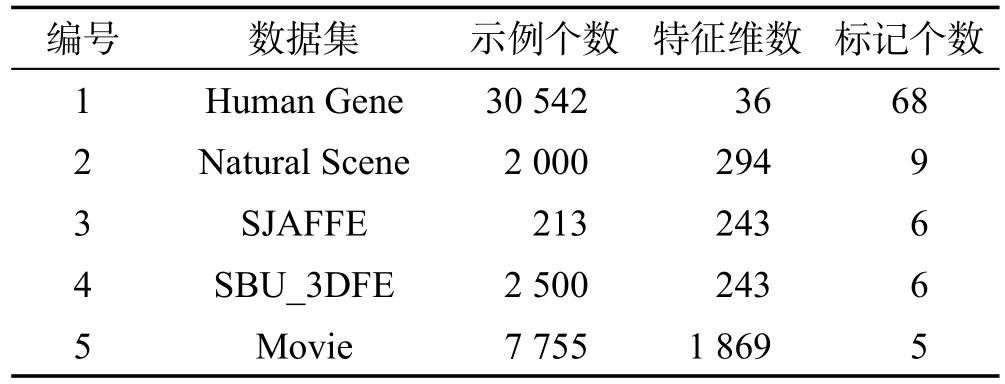
Table 2 5 real label distribution learning datasets表2 5个真实标记分布学习数据集
1号数据集是人类基因数据集,每个示例代表一种人类基因。文献[22]给出了基因特征的提取方法。通过对一种基因在68种疾病中的基因表达强度进行归一化,可以得到示例的标记分布。
2号数据集是自然场景数据集。数据集中每个示例代表一幅自然场景图片,示例的特征使用文献[21]的方法得到。每个示例原本对应的是具有9个标记的排序集合(由10个人给出的排序),排序的依据是标记和图片的相关程度。通过文献[23]的方法可以将排序集合转换为标记分布。
3号和4号数据集是两个人类表情数据集JAFFE[24]和BU_3DFE[25]。示例的特征是使用文献[25]的方法处理得到的。一共有6个标记,代表6种人类的表情分别是开心、难过、惊讶、害怕、生气及厌恶。示例的标记分布是通过以下过程得到的。首先请多个不同的人根据图片中的人脸表情对6种表情进行打分,分数分成5个级别,级别越高,对应表情越符合图片中的人脸表情。最后对分数进行归一化得到标记分布。
5号数据集是一个电影评分数据集。数据集的每个示例代表一部电影。一个示例的特征是根据电影的类别、导演、主演及预算等信息生成的特征向量。一部电影的评分有5个级别,相当于有5个标记。将每个级别的评分人数占总评分人数的比例作为对应标记的描述度,则可以生成一个标记分布。
4.3 实验方法
本文用所选的7个代表距离作为目标函数,以最大熵模型作为标记分布输出模型,优化方法使用BFGS算法,对泛化标记分布学习框架进行特化,得到7种具体算法。为了简便,采用目标函数所用的距离名称代表对应的算法。为了比较这些算法的预测效果,在5个真实标记分布数据集上进行实验。实验过程采用十倍交叉验证。如前面提到的一样,7个代表距离同时作为评价指标,实验结束后会得到每种算法7种评价指标各自的平均值和标准差,通过平均值和标准差可以对7种算法进行排序。对5个数据集的实验结果进行汇总后,可以得到一个具有统计意义的实验结果,本文将对实验结果进行观察和分析。
4.4 实验结果与分析
表3~表7分别给出了5个数据集的实验结果。表格中的每一行对应一种算法的实验结果,每一列对应一种评价指标的实验结果。为了简便,表格中距离的名称使用了简写,简写和全称的对应关系为:KL对应Kullback Leibler,Pear对应Pearson,Dive对应Divergence,Canb对应Canberra,Kdiv对应K divergence,SE对应Squared Euclidean,CB对应City block。表中的实验结果形式为:平均值±标准差。表中7个评价指标均为距离,数值越小表示预测效果越好。每个实验结果后面有一个括号括起的数字,代表对应算法在对应评价指标上的表现排名,表现越好排名越靠前。例如在表3中,K divergence算法的Kullback Leibler评价指标平均值是7个算法中最小的,则对应的括号里的数字为1,表示其表现最好。每个表格的最后一列给出的是平均排名,表示一个算法在7个评价指标上的排名的平均值。为了方便观察排名最好的算法,每张表中把每个评价指标上排名第一的实验结果加黑。平均排名最好的算法和其平均排名也加黑。
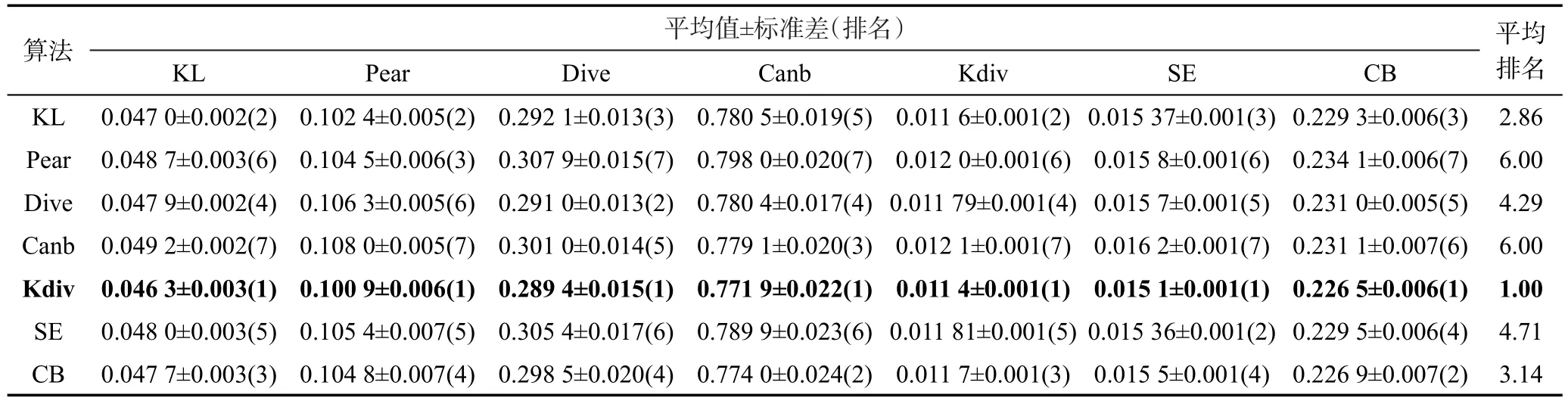
Table 3 Experimental results on SBU_3DFE dataset表3 SBU_3DFE数据集实验结果
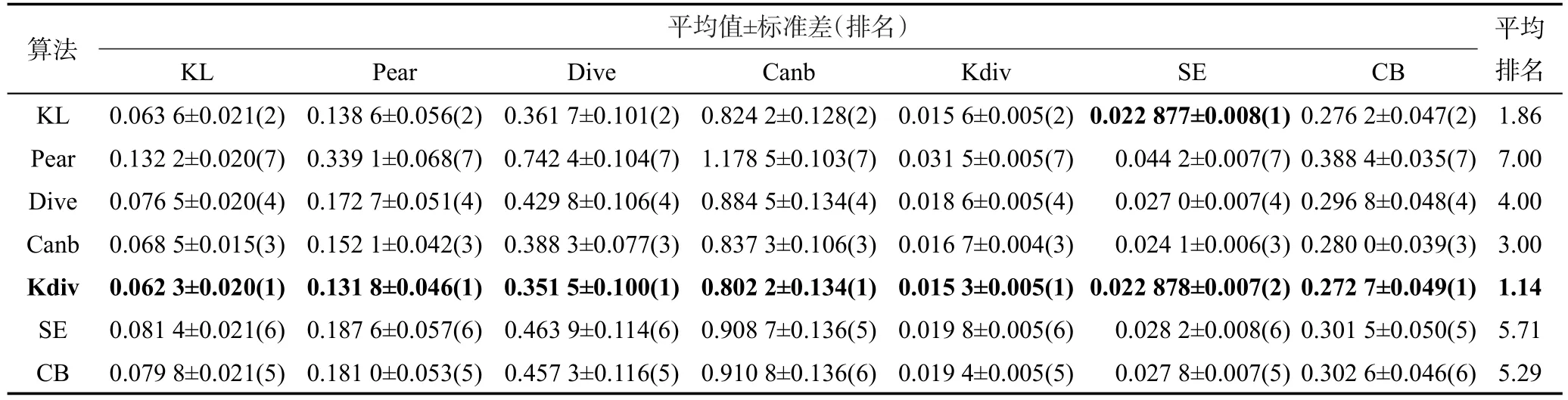
Table 4 Experimental results on SJAFFE dataset表4 SJAFFE数据集实验结果
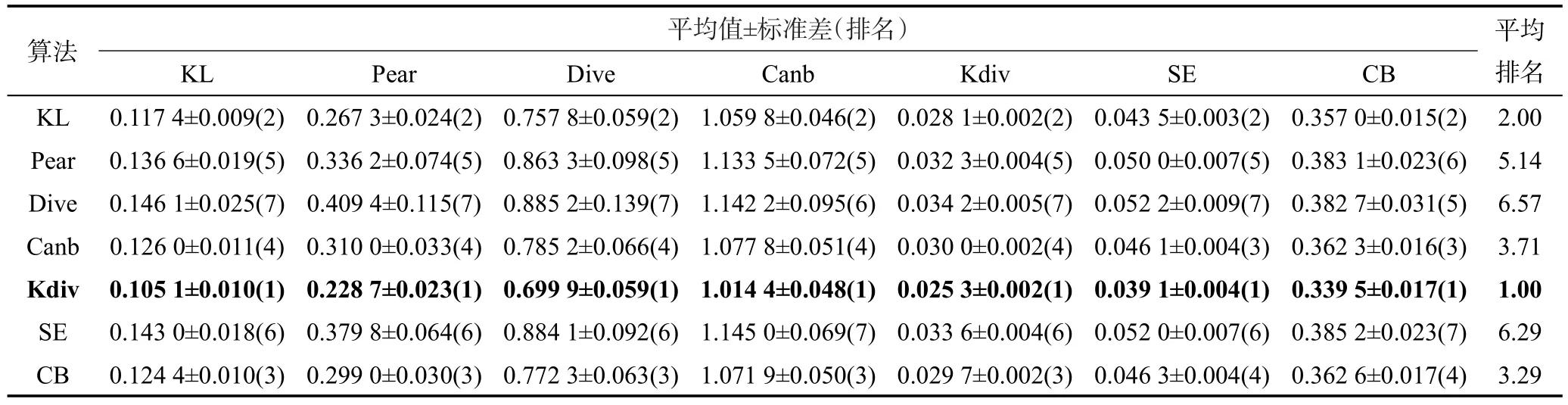
Table 5 Experimental results on Movie dataset表5 Movie数据集实验结果
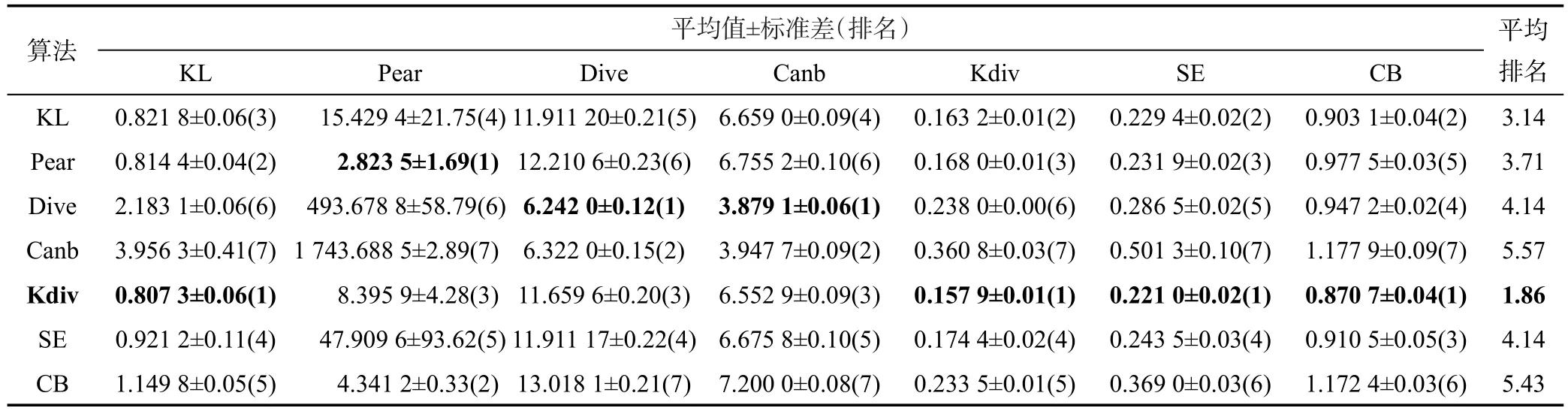
Table 6 Experimental results on Natural Scene dataset表6 Natural Scene数据集实验结果
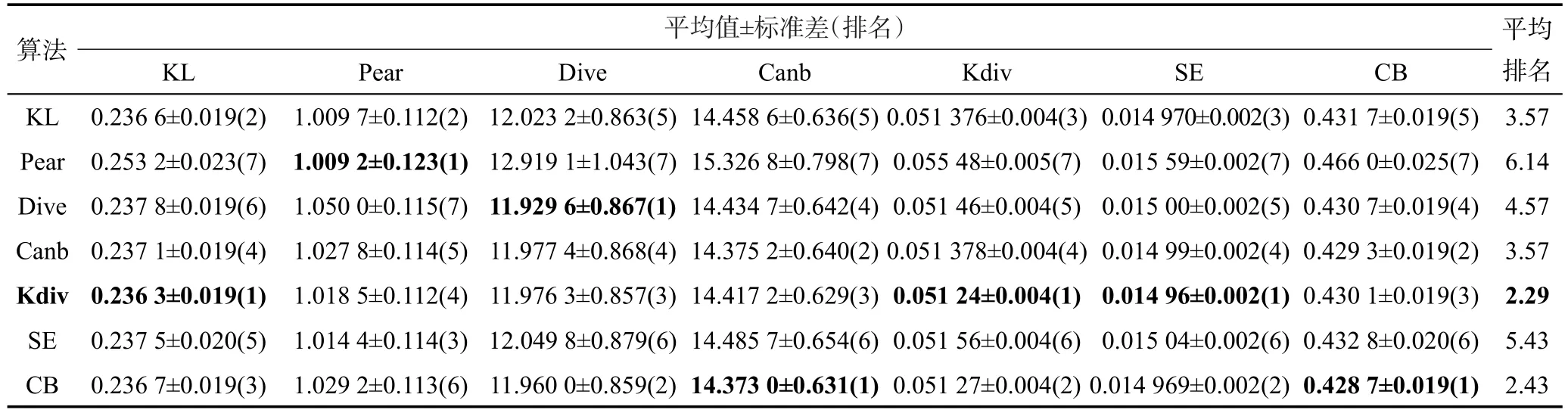
Table 7 Experimental results on Human Gene dataset表7 Human Gene数据集实验结果
在表6给出的Natural Scene数据集的实验结果中,观察Pear评价指标列中的数据,可以发现一些比较大的数值,例如Canberra算法的数值达到了1 000以上。这些较大的数值和同一列中的其他数值在数量级上并不统一。而其他评价指标列中的数值在数量级上是比较统一的。出现这种现象并不是实验和算法本身的问题,而是与数据集及Pearson距离公式的特点有关系。Natural Scene数据集示例的真实标记分布中出现了大量描述度接近于0的分量,使得训练完后的最大熵模型,对于新示例倾向于输出包含较多的描述度接近于0的分量的标记分布。Pearson距离公式(如表1所示)用预测描述度做分母,当预测描述度较接近于0,且真实描述度较大时,就相当于用真实描述度的平方除以预测描述度。因此,当真实分布中和预测分布中那些描述度接近于0的分量对应的描述度较大时(由于真实分布中会出现很多描述度接近于0的分量,加上所有分量的描述度和为1,因此会出现一些描述度比较大的分量),用Pearson距离公式计算出的值就会比较大。这说明Pearson距离对分布中包含较多描述度接近于0的分量的数据集的测试结果变化起伏较大。
虽然在Natural Scene数据集中Canberra算法在Pear指标上的表现并不理想,但是其在Dive和Canb两个指标上的表现却不错。类似的情况在所提供的实验结果中是普遍存在的。这一现象说明,和多标记学习一样,评价一个标记分布学习算法预测效果的好坏不能单纯只看一项指标,需要用不同的指标从不同的侧面进行反映。
仔细观察5个数据集的实验结果可以发现,在某些指标上,两个排名相邻的算法的指标平均值比较接近。例如:在Human Gene数据集中,K divergence算法和Kullback Leibler算法的KL评价指标平均值就十分接近(和标准差的数量级不匹配)。虽然存在这种现象,但是选择不同的距离作为目标函数并非对算法的预测效果没有影响。例如:在Human Gene数据集中K divergence算法和Kullback Leibler算法的KL评价指标平均值虽然比较接近,但是在0.05的显著性水平条件下,对在十倍交叉验证过程中得到的10次实验结果进行T检验,能够得出两个算法在KL评价指标上存在显著性差异的结论。这说明选择不同距离作为目标函数对算法的预测效果还是有影响的。
观察5个数据集的实验结果可以发现,K divergence和Kullback Leibler两个算法的平均排名一般情况下都会好于其他算法,尤其是K divergence算法在5个数据集中的平均排名都是最好的。本文将5个数据集的实验结果汇总成表8。表8的每一行对应一种算法,每一列对应一种评价指标。表8中的数字表示一个算法在5个数据集中排名的平均值。最后一列给出的是一个算法的7个指标的平均排名(对应5个数据集)的平均值。为了更加直观地对比不同算法的预测效果,本文将表8中的排名转换为灰度表示,如图4所示。图4中色块的灰度和表8中的平均排名相对应,色块越白表示排名越靠前,反之则越靠后。通过表8和图4可以看出,在统计意义上K divergence和Kullback Leibler两个算法的效果是最好的。通过表1分析7个代表距离计算公式上的特点,可以发现这7个代表距离大致可以分为两类:第一类距离是基于真实描述度和预测描述度的比值的对数来度量两个分布的不相似程度,这类距离有K divergence和Kullback Leibler。第二类距离是基于真实描述度和预测描述度的差来度量两个分布的不相似程度,这类距离包括除两个第一类距离外的剩余5个距离。两类距离度量不相似程度的基本方法不同,导致了以其为目标函数的标记分布学习算法的预测效果不同。以第二类距离为目标函数的算法,会倾向于学习描述度高的标记。这是因为减少描述度高的标记的预测误差将能减少更多第二类距离的值。以第二类距离为目标函数的算法的这种学习倾向会导致在训练过程中忽略对描述度低的标记的学习,这显然是不合适的。在标记分布学习问题中,希望预测的是一个整体的标记分布,而不是只单纯预测描述度高的标记。第一类距离则不会出现这种问题。虽然第一类距离以标记的真实描述度为权重,也倾向于学习描述度大的标记,但是通过求比值的对数的方式,减小描述度小的标记的预测误差仍能较为明显地减小第一类距离的值,使得这种倾向控制在合理范围内。
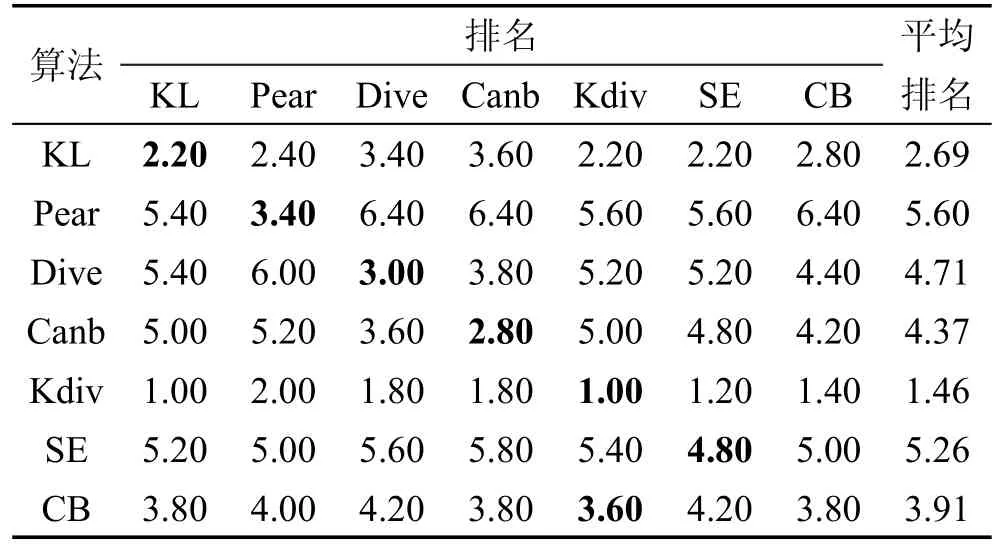
Table 8 Summary of average rank of 7 algorithms表8 7个算法的平均排名汇总

Fig.4 Gray scale image of average rank of 7 algorithms图4 7个算法平均排名灰度图
在第一类距离中,K divergence算法的效果要优于Kullback Leibler算法。图5展示的是K divergence和Kullback Leibler距离的变化曲线,其中绿色实线表示K divergence距离,红色虚线表示Kullback Leibler距离。以一个只有两个标记的标记分布{0.5, 0.5}为真实分布。通过将一个标记的描述度在0.01到0.99的范围内按0.01的步长连续变化,可以得到一个预测分布集合。通过计算真实分布和预测分布集合的距离值得到图5中的变化曲线。图5的纵坐标代表距离的值,横坐标表示预测分布中一个标记的描述度。通过图5不难发现,在预测较不准确的情况下(图5中曲线的两端部分),K divergence距离的变化曲线更加平坦。当预测较为准确时(图5中曲线的中间部分),两个距离的变化曲线是十分相似的,这一点通过表1中两者的计算公式也可以看出来。以上两点说明,当快接近于最优参数值时,两个距离的变化曲面是近似等价的,以两个距离作为目标函数的标记分布学习算法都能找到相似的最优参数。而当处于极端情况时,K divergence距离平坦的变化曲线意味着以模型参数为自变量形成的局部最优曲面深度会较浅,当算法陷入局部最优值后能更容易地迭代出来。这就是K divergence算法预测效果比Kullback Leibler算法预测效果好的原因。
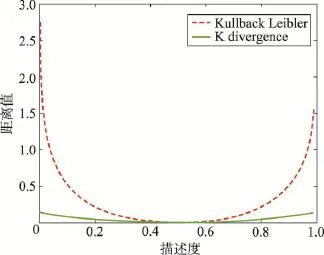
Fig.5 Changing curves of K divergence and Kullbacd Leibler图5 K divergence和Kullback Leibler距离变化曲线
分别观察表8中的每一列数据还可以发现,在每个评价指标上表现最好或次好的算法一般都是用和该评价指标相同的距离作为目标函数的算法。例如:Divergence算法在Dive评价指标上的平均排名是除K divergence算法外最好的。继续观察每一行还可以发现,在7个评价指标中,一个算法平均排名最靠前的评价指标一般都是这种算法用来作目标函数的距离所对应的指标。把表8每一行中最靠前的平均排名加黑,可以发现表8基本呈现出一条对角线。从图4中则可以观察到,对角线上的色块要相对偏白。这说明以某个距离作为目标函数的算法倾向于优化这个距离。反过来也可以说明,在某些情况下,想要使预测的标记分布在某个距离上表现最好,可以使用这个距离作为目标函数来特化泛化框架设计算法。例如:在表6中观察Pear评价指标对应的列,可以发现Pearson算法的效果是最好的,说明以Pearson距离为目标函数的算法能比其他算法更好地优化Pearson距离。
4.5 选取合适的目标函数
基于以上的分析,对于在通过泛化标记分布学习框架设计算法的过程中如何选择目标函数,本文提出以下几点建议:一个算法输出的标记分布预测效果怎样,从表3到表8的实验结果和前面的分析可以看出,是不能只用单一的评价指标来评价的。不同的评价指标从不同的侧面反映一个算法的预测效果。例如:前面提到的第二类距离,受描述度大的标记影响较大,倾向于反映描述度大的标记的预测效果。而第一类距离则从整体的分布反映一个算法的预测效果。因此在选择目标函数时,首先需要确定更关注算法哪方面的预测效果。如果希望算法能更好地预测描述度大的标记的描述度,则可以用第二类距离作为预测效果的评价指标,并且选择第二类距离中的距离作为目标函数。例如:在Natural Scene数据集中,存在不少包含大量值接近于0的分量的标记分布,在这些标记分布中只有少数几个标记的描述度较大,而其他标记的描述度则十分接近于0。此时,可以只关注对这些描述度大的标记的预测效果,因此选用Pear指标作为预测效果的评价指标。同时,如表6中Pear列的数据所示,Pearson算法在Pear评价指标上的效果是最好的,因此可以同时选择Pearson距离作为目标函数。如果关注的是算法的综合性能,希望算法既给予描述度高的标记较大的学习权重,同时又兼顾对描述度小的标记的学习,则可以考虑使用第一类距离作为目标函数。通过实验和分析,本文发现以K divergence作为目标函数能获得更好的综合表现,因此在第一类距离中,本文更推荐使用K divergence距离。
5 结束语
本文针对一种较为有效的标记分布学习算法设计策略,提出了一种泛化标记分布学习框架。这个泛化框架主要由输出模型、目标函数和优化方法三部分组成。通过三部分的不同组合,可以特化出不同的标记分布学习算法。然后,本文以目标函数部分为研究对象,通过在5个真实标记分布数据集上进行实验,分析了目标函数和评价指标间的关系,及以不同的距离作为目标函数对算法预测效果的影响。最后,本文基于这些分析,就在使用泛化标记分布学习框架设计算法时如何选择目标函数这一问题,提出了一些建议。本文对于泛化框架中的输出模型和优化方法两部分并未进行深入研究,这两部分的设计对一个标记分布学习算法来说是十分重要的,因此有待进一步的研究。
[1]Tsoumakas G,Katakis I.Multi-label classification:an overview[J].International Journal of Data Warehousing and Mining,2007,3(3):1-13.
[2]Tsoumakas G,Zhang Minling,Zhou Zhihua.Tutorial on learning from multi-label data[C]//Proceedings of the 2009 European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases,Bled,Slovenia, Sep 7-11,2009.Berlin,Heidelberg:Springer,2009.
[3]Read J,Pfahringer B,Holmes G,et al.Classifier chains for multi-label classification[J].Machine Learning,2011,85(3): 333-359.
[4]Hüllermeier E,Fürnkranz J,Cheng W,et al.Label ranking by learning pairwise preferences[J].Artificial Intelligence, 2008,172(16):1897-1916.
[5]Read J,Pfahringer B,Holmes G.Multi-label classification using ensembles of pruned sets[C]//Proceedings of the 8th IEEE International Conference on Data Mining,Pisa,Italy, Dec 15-19,2008.Washington:IEEE Computer Society,2008: 995-1000.
[6]Cheng Weiwei,Hüllermeier E.Combining instance-based learning and logistic regression for multilabel classification [J].Machine Learning,2009,76(2):211-225.
[7]Clare A,King R D.Knowledge discovery in multi-label phenotype data[C]//LNCS 2168:Proceedings of the 5th European Conference on Principles of Data Mining and Knowledge Discovery,Freiburg,Germany,Sep 3-5,2001.Berlin, Heidelberg:Springer,2001:42-53.
[8]Sapozhnikova E P.ART-based neural networks for multi-label classification[C]//Proceedings of the 8th International Symposium on Intelligent Data Analysis,Lyon,France,Aug 31-Sep 2,2009.Berlin,Heidelberg:Springer,2009:167-177.
[9]Geng Xin,Ji Rongzi.Label distribution learning[C]//Proceedings of the 13th International Conference on Data Mining Workshops,Dallas,USA,Dec 7-10,2013.Washington:IEEE Computer Society,2013:377-383.
[10]Zhang Zhaoxiang,Wang Mo,Geng Xin.Crowd counting inpublic video surveillance by label distribution learning[J]. Neurocomputing,2015,166(C):151-163.
[11]Geng Xin,Yin Chao,Zhou Zhihua.Facial age estimation by learning from label distributions[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35 (10):2401-2412.
[12]Geng Xin,Xia Yu.Head pose estimation based on multivariate label distribution[C]//Proceedings of the 2014 IEEE International Conference on Computer Vision and Pattern Recognition,Columbus,USA,Jun 23-28,2014.Washington:IEEE Computer Society,2014:1837-1842.
[13]Geng Xin,Wang Qin,Xia Yu.Facial age estimation by adaptive label distribution learning[C]//Proceedings of the 22nd International Conference on Pattern Recognition,Stockholm,Sweden,Aug 24-28,2014.Washington:IEEE Computer Society,2014:4465-4470.
[14]Geng Xin,Smith-Miles K,Zhou Zhihua.Facial age estimation by learning from label distributions[C]//Proceedings of the 24th AAAI Conference on Artificial Intelligence,Atlanta, USA,Jul 11-15,2010.Menlo Park,USA:AAAI,2010:451-456.
[15]Geng Xin,Hou Peng.Pre-release prediction of crowd opinion on movies by label distribution learning[C]//Proceedings of the 2015 International Joint Conference on Artificial Intelligence,Buenos Aires,Argentina,Jul 25-31,2015. San Francisco,USA:Morgan Kaufmann,2015:3511-3517.
[16]Berger A L,Pietra V J D,Pietra S A D.A maximum entropy approach to natural language processing[J].Computational Linguistics,2002,22(1):39-71.
[17]Pietra S D,Pietra V D,Lafferty J.Inducing features of random fields[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(4):380-393.
[18]Nocedal J,Wright S.Numerical optimization[M].2nd ed. New York:Springer,2006.
[19]Cha S H.Comprehensive survey on distance/similarity measures between probability density functions[J].International Journal of Mathematical Models and Methods in Applied Sciences,2007,1(4):300-307.
[20]Duda R O,Hart P E,Stork D G.Pattern classification[M]. New York:John Wiley&Sons,2012.
[21]Liu Jun,Yuan Lei,Ye Jieping.An efficient algorithm for a class of fused Lasso problems[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Washington,Jul 25-28,2010. New York:ACM,2010:323-332.
[22]Yu Jiafeng,Jiang Dongke,Xiao Ke,et al.Discriminate the falsely predicted protein-coding genes in aeropyrum pernix K1 genome based on graphical representation[J].Match Communications in Mathematical and in Computer Chemistry, 2012,67(3):845-866.
[23]Geng Xin,Luo Longrun.Multilabel ranking with inconsistent rankers[C]//Proceedings of the 2014 IEEE International Conference on Computer Vision and Pattern Recognition, Columbus,USA,Jun 23-28,2014.Washington:IEEE Computer Society,2014:3742-3747.
[24]Lyons M,Akamatsu S,Kamachi M,et al.Coding facial expressions with gabor wavelets[C]//Proceedings of the 1998 IEEE International Conference on Automatic Face and Gesture Recognition,Nara,Japan,Apr 14-16,1998.Washington: IEEE Computer Society,1998:200-205.
[25]Yin Lijun,Wei Xiaozhou,Sun Yi,et al.A 3D facial expression database for facial behavior research[C]//Proceedings of the 10th IEEE International Conference on Automatic Face and Gesture Recognition,Southampton,UK,Apr 10-12,2006.Washington:IEEE Computer Society,2006:211-216.

ZHAO Quan was born in 1990.He is an M.S.candidate at School of Computer Science and Engineering,Southeast University.His research interests include data mining and machine learning.
赵权(1990—),男,海南东方人,东南大学计算机科学与工程学院硕士研究生,主要研究领域为数据挖掘,机器学习。

GENG Xin received the M.S degree from Nanjing University in 2004,the Ph.D.degree from Deakin University of Australia in 2008.Now he a professor and vice dean at School of Computer Science and Engineering,Southeast University,and the member of CCF.His research interests include pattern recognition,machine learning and computer vision.He has published over 40 refereed papers and holds 4 patents in these areas.
耿新,2004年于南京大学计算机科学与技术系获得硕士学位,2008年于澳大利亚Deakin大学获得博士学位,现为东南大学计算机科学与工程学院教授、副院长,CCF会员,主要研究领域为模式识别,机器学习,计算机视觉。发表学术论文40余篇,获得4项授权发明专利。
Selection of Target Function in Label Distribution Learning*
ZHAO Quan1,2,GENG Xin1,2+
1.Key Laboratory of Computer Network and Information Integration(Southeast University),Ministry of Education, Nanjing 211189,China
2.School of Computer Science and Engineering,Southeast University,Nanjing 211189,China
+Corresponding author:E-mail:xgeng@seu.edu.cn
ZHAO Quan,GENG Xin.Selection of target function in label distribution learning.Journal of Frontiers of Computer Science and Technology,2017,11(5):708-719.
Label distribution learning is a new machine learning paradigm proposed in recent years.In theory,this paradigm can be seen as a generalization of multi-label learning paradigm.Previous studies show that label distribution learning paradigm is an effective learning paradigm.It can solve some label ambiguity problems effectively. For label distribution learning,a number of special algorithms which have good prediction effect have been proposed.For these special algorithms,this paper proposes a generalization frame of label distribution learning.In this learning frame,a special algorithm consists of three parts,they are target function,output model and optimization algorithm.This paper studies the part of target function in this generalization frame.In order to study the relationship between prediction effect of a label distribution learning algorithm and different target functions,this paper selects 7 representative distances.Based on the characteristics of each distance and experiment results of 5 real label distribution learning datasets,this paper proposes some suggestions how to choose a target function.
label distribution learning;maximum entropy model;quasi-Newton method;selection of target functions
10.3778/j.issn.1673-9418.1603051
A
:TP391
*The National Natural Science Foundation of China under Grant Nos.61273300,61232007(国家自然科学基金);the Natural Science Funds for DistinguishedYoung Scholar of Jiangsu Province under Grant No.BK20140022(江苏省自然科学基金杰出青年基金项目).
Received 2016-03,Accepted 2016-05.
CNKI网络优先出版:2016-05-13,http://www.cnki.net/kcms/detail/11.5602.TP.20160513.1434.006.html
摘 要:标记分布学习是近年提出的一种新的机器学习范式。从理论上来说,这一范式可以看作是对多标记学习的泛化。已有的研究表明标记分布学习是一种有效的学习范式,能够很好地解决某些标记多义性问题。针对标记分布学习,已有一些预测效果不错的专门算法被提出来。针对这些专门的标记分布学习算法提出了一种泛化标记分布学习框架。在这个框架中,一个专门的标记分布学习算法由目标函数、输出模型和优化方法三部分组成。针对这个泛化框架中的目标函数部分展开研究。为了研究选择不同的距离作为目标函数对标记分布学习算法预测效果的影响,选取7个代表性距离作为研究对象。通过对5个真实标记分布数据集上的实验结果进行分析,结合每个距离的特点,提出了一些选取目标函数的具体建议。

