基于贝叶斯网的知识图谱链接预测*

韩 路，尹子都，王钰杰，胡 矿，岳 昆+

1.云南大学 信息学院，昆明 650504

2.云南大学 信息技术中心，昆明 650504

基于贝叶斯网的知识图谱链接预测*

韩 路1，尹子都1，王钰杰1，胡 矿2，岳 昆1+

1.云南大学 信息学院，昆明 650504

2.云南大学 信息技术中心，昆明 650504

结合外部知识，使用特定方法进行知识图谱的链接预测，即知识图谱中缺失信息的发现和还原，是目前知识图谱领域研究的热点和关键。以电子商务应用为背景，基于已经构建好的描述用户兴趣的知识图谱，结合外部数据集，以贝叶斯网这一重要概率图模型作为不同商品之间相似性及其不确定性的表示和推理框架，通过对商品属性进行统计计算，构建反映商品之间相似关系的贝叶斯网，进而基于概率推理机制，定量地判断商品节点与用户节点之间存在链接的真实性，得到真实和完整的知识图谱，为个性化推荐和关联查询提供依据。建立在真实数据上的实验结果表明，提出的模型和算法是有效的。

知识图谱；链接预测；贝叶斯网；相似性；概率推理

1 引言

随着信息技术的不断发展和成熟，Web技术正在从网页之间的链接向包含各种实体以及实体之间关系的数据链接转变，传统的文本万维网逐步发展成为数据万维网，互联网公司逐步开始以此为基础构建知识图谱（knowledge graph，KG）[1]。借助KG，人们可以从过去单一的网页链接转向实体链接：基于KG的搜索引擎，通过图结构反馈知识，帮助用户简单精确地实现知识的获取和定位，从而实现真正意义上的语义搜索[2]。KG是一种由节点和边组成的图结构，本质上是由数据构成的语义网[3]。KG中的节点对应现实世界中存在的实体，节点之间的边代表实体之间的关系。KG的研究涉及自然语言处理、机器学习和数据挖掘等多个领域的知识，基于KG的数据挖掘是未来相关研究的趋势[4]。

网络关系的链接预测是数据挖掘和机器学习领域中一个新兴的课题[5]，它是指如何通过网络中已知的节点以及网络结构等信息来预测网络中无边相连的两个节点之间产生链接关系的可能性，能为缺失信息还原和错误信息检测提供支撑技术[6]。

目前，KG研究主要包括如下两方面：（1）KG的构建，其中包含信息抽取、知识融合等多个过程[7]。（2）KG中知识的推理，KG上的规则主要是针对关系的，即通过规则（一般为链式规则）发现实体之间隐含的关系[1]。

KG链接预测是KG推理领域的研究方向之一[8]，由于数据来源广泛，尤其是Web数据更加杂乱，构建KG的源数据中往往存在大量错误及缺失信息。对于存储KG的知识库而言，尽管拥有大规模的数据，但许多数据库仍然不完整，例如，Google Knowledge Vault项目[9]中的核心元素Freebase[10]中，71%的个人信息缺失“出生地”，75%缺失“国籍说明”等。通过链接预测，可以发现现有KG中缺失和错误的信息，得到更为完整和真实的KG，进而更新知识库。具体而言，KG链接预测主要涉及如下两方面的任务[5]：

（1）预测异常链接。由于数据来源的复杂性，现有KG存在部分错误边的情况，通过链接预测可以发现异常链接，进而得到更为真实的KG。

（2）预测未知链接。针对预测查询或搜索服务，来预测KG中尚未包含的链接。

例如，图1所示的KG描述了用户对电影兴趣的KG，未知链接预测的任务是判断图中虚线边是否真实存在，异常链接预测旨在发现已经存在，但其存在概率很低且可能需要删除的链接关系。

近年来，对于链接预测相关问题，国内外学者开展了较为全面和系统的研究。例如，Getoor等人[11]系统地综述了链接挖掘的相关概念和研究领域，介绍了链接预测的问题、定义和经典模型。对于KG中的链接预测，目前大多数方法都是基于组成KG的RDF（resource description framework）三元组进行，而基于KG图结构的链接预测方法仍有待进一步深入研究。Bordes等人[12]提出了TransE模型，将KG中的关系看作实体间的某种向量；Drumond等人[13]利用张量分解对不完整KG中的RDF三元组进行预测，从而支持KG的更新；Socher等人[14]提出了基于神经网络的方法，应用于链接预测，但方法的复杂性和模型训练及参数调优是其主要缺点；Richardson等人[15]定义了马尔科夫逻辑网，基于逻辑准则定义KG潜在函数语言的方法，从而进行链接预测，但规则学习以及参数估计成为其应用中的瓶颈。同时，现有方法对于KG中尚未描述但又必须的知识获取及融合还有许多不足之处，且对于链接关系存在的可能性或不确定性不能较好地进行定量计算。

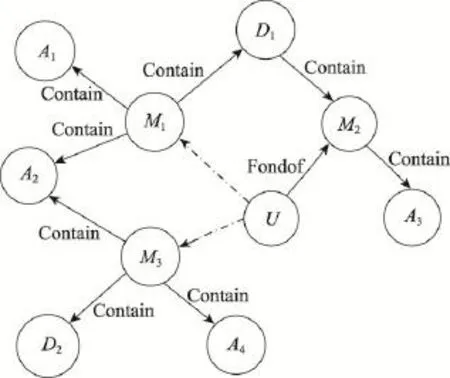
Fig.1 KG of user interest on movies图1 用户对电影兴趣的KG

贝叶斯网（Bayesian network，BN）[16]是典型的概率图模型[17]，同时考虑了网络结构和节点属性信息，具有坚实的概率论理论基础和广泛应用[18]。适用于表达和分析不确定性知识，能够对不确定性知识做出有效的推理，是目前不确定知识表达和推理领域最有效的模型之一[19]。KG中实体之间的相互关系存在不确定性，通过BN的概率推理可以发现这种不确定性。同时，KG中链接预测的实质是通过KG中已有的链接对未知链接进行判断，这是BN的优势所在。

事实上，除了KG中描述的知识外，现实世界中存在许多与KG相关联的外部知识（例如描述商品类型的标签数据集），这些知识中存在大量人们已经构建好的丰富的先验知识，可以提供更为全面和真实的信息，KG中提供的数据与外部知识结合，可提高KG链接预测的准确性。

本文从已有KG出发，结合标签数据集外部知识，构建链接贝叶斯网（link Bayesian network，LBN）模型，基于LBN进行概率推理，从而完成KG链接预测的任务。

具体而言，本文的研究主要包括如下几方面：

（1）针对KG中属性节点单一，数据量不够充分的特点，引入与KG相关联的描述商品类别的标签数据集这一外部知识，以便实现将KG中数据和外部数据集结合。标签数据中对应描述KG中商品实体的标签，可以充分用于表达商品之间的相似性，提高链接预测的准确性。

（2）为了描述商品节点之间的相似性，利用商品属性，构建针对KG链接预测的LBN。将KG和标签数据集相结合而构成的商品属性，构建描述商品之间相关性的LBN，作为BN概率推理及链接预测的基础。

（3）针对KG的链接预测，当KG中节点较多且链接比较紧密时，构建的LBN的规模也会随之增大。Gibbs采样是应用最广泛的马尔科夫链蒙特卡罗（Markov chain Monte Carlo，MCMC）概率算法，可有效地获取一系列近似等于指定多维概率分布的观察样本[20-21]。为了实现基于LBN的高效链接预测，本文基于Gibbs采样给出了LBN的概率推理算法，量化了未知链接真实存在的可能性，基于此实现了KG的链接预测。

（4）基于MovieLens站点数据（http://grouplens. org/），本文实现并测试了LBN的构建、近似推理和链接预测方法的有效性。

本文组织结构如下：第2章描述KG链接预测问题，并给出LBN的定义；第3章讨论构建LBN模型的方法；第4章研究基于LBN的近似推理算法和KG链接预测方法；第5章给出实验结果和性能分析；第6章总结全文并展望将来的工作。

2 问题描述和相关定义

根据用户浏览信息可以针对特定用户构建个性化的用户兴趣KG，通过链接预测，可以获得更加完整的KG，进一步应用于查询和个性化推荐等，从而实现KG对于用户的核心价值。对于描述用户兴趣的KG，用户和商品之间的联系是研究的重点：为了进行链接预测，借助已有的联系以及商品属性，发现用户和不存在链接商品之间的关系，是本文研究的核心。KG本质上是一种基于图的数据结构，首先给出KG的形式化定义。

定义1（KG）KG用Gk=(V,E)表示，其中V={v1, v2,…,vn}表示KG中实体对应节点的集合，E={e1, e2,…,en}表示实体之间边的集合。任意一条边对应一个节点二元组ex={vi,vj}，节点vi称为始点，节点vj称为终点。

用户兴趣KG主要包括用户、商品和商品属性信息3类实体。KG中的节点分别代表不同实体，与实体类型对应，集合V中节点也对应这3种类型。

对于Gk的节点集合V，用U表示其中的用户节点，O={O1,O2,…,Om}表示商品节点集合，Si={s1,s2,…,sk} (1≤i≤m)表示商品节点Oi在Gk中对应的属性节点集。

例1图1为用户电影兴趣KG，图中节点分为用户、电影以及电影属性3类，该KG中的电影属性主要包括演员和导演等。其中，用户节点为U，电影实体集合为O={M1,M2,M3}。M1对应的属性信息集合S1= {A1,A2,A3}。

此外，KG中实体之间的相互关系存在不确定性，这种不确定性体现在Gk对应边上，即Gk中的边以一定的概率真实存在。需要对这种不确定性进行量化，作为链接预测的依据，为此引出可信度的概念。

定义2（可信度）KG图结构Gk中的边真实存在的概率值称为可信度。对于有向边{vi,vj}，用Wij表示其可信度。

可信度越大，表示对应链接存在的可能性越大。给定阈值ε，对应特定的链接进行可信度计算，可信度大于等于ε的认为其真实存在，若可信度小于阈值ε，则忽略。Gk中已有边的可信度都大于等于ε，是本文讨论的前提。

BN是一个DAG（directed acyclic graph）Gb=(V, E)，其中V代表随机变量节点集，每一个节点对应一个随机变量，E中的有向边用来表示节点之间的条件依赖关系。V中的每一个变量都有一个条件概率表（conditional probability table，CPT），用来表示已知父亲节点状态来计算当前状态的概率。基于BN的基本概念，提出LBN模型，作为链接预测的模型基础。下面给出LBN的定义。

定义3（LBN）LBN用一个二元组G=(Gl,P)表示，其中：

（1）Gl=(Ol,El)为LBN的DAG结构，Ol={O1,O2,…, Om}为节点集合，每个节点对应KG中的一个商品节点，有向边集El为节点之间相似关系的集合。Oi(1≤i≤m)取值为1或0，分别表示Oi在Gk中是否和用户节点U之间存在链接。若存在有向边{Oi,Oj}，则称Oi为Oj的一个父节点，Oj的父节点集记为Pa(Oi)。

（2）P={p(Oi|Pa(Oi)|Oi∈O)}为条件概率分布的集合，由各节点CPT中概率参数值构成，p(Oi|Pa(Oi))表示节点Oi在其父节点的影响下的条件概率，用来描述Pa(Oi)的状态对Oi的影响。

本文构建商品属性之间相似关系的LBN。对于图1中的用户兴趣KG而言，描述商品属性的信息较少，而且比较单一，无法充分表达商品节点之间的相似性。本文引入标签数据集D（所谓标签即商品所对应的类型）这一“外部知识”。D中主要描述的是KG中集合O的商品实体对应的标签类型信息：数据集D中一条商品的标签类型记录Item可以表示为{Oi,Ti,Li}，其中Oi(1≤i≤m)用以标识KG中商品集合O中的实体，Ti表示Oi对应商品的名称，Li={l1,l2,…, ln}表示Oi所对应的标签。

图1中KG对应的数据集D如表1所示。商品节点Oi(1≤i≤m)的属性内容可表示为一个二元组Ci=＜Oi,Bi＞，其中属性Bi由KG中的节点集合Si和数据集D中的Li共同组成，即Bi=Si⋃Li(1≤i≤n)。

Table 1 Data of labels表1 标签数据集

例2对于商品节点M2而言，KG中对应的节点集合S2={D1,A3}，数据集D对应的标签为L2={l1,l4,l5, l8}，则C2=＜M2,{l1,l4,l5,l8,D1,A3}＞。

3 LBN的构建

构建LBN，首先构建其DAG。基于构建的DAG，可以发现商品节点之间的相似关系，从而基于此进行概率推理。以下讨论基于Gk和标签数据集D来构建LBN的DAG的方法。

3.1 节点选取

LBN的Gl基于KG中商品节点之间的相似性而构建，因此Ol由KG中的商品节点组成。构建DAG的第一步是选取商品节点，对于Gk中的商品节点，与其相关联的边数多于其余类型的节点。为此，引入节点度的概念，作为选取特定节点的重要依据之一。

定义4（节点度）节点度d是指和该节点相关联的边的条数。对于类似KG的有向图而言，节点Oi的入度dp(Oi)是指进入该节点的边的条数，节点的出度do(Oi)是指从该节点出发的边的条数，d(Oi)为入度和出度之和。

本文通过判断节点度的大小来获取集合O中的节点，对于给定的KG，设置节点度d，遍历KG中的所有节点，依次求节点的节点度，对于节点度不小于d的节点，加入到集合Ol中，直到遍历结束，输出集合Ol。

例3由图1可知，“电影”节点对应的最小节点度d=3，依次遍历Gk节点集V中的所有节点，将节点度不小于d的节点添加到集合Ol中，然后输出Ol，从而可以得到Ol={M1,M2,M3}。

3.2 DAG的构建

LBN中有向边的集合El描述节点间的相似关系，DAG的构建包括如下三方面的问题：（1）确定商品对应节点间是否存在边，即判断商品是否相似；（2）若商品之间存在相似关系，则要确定对应节点之间边的方向；（3）构建DAG的过程中保证不出现环。

针对问题（1），对于任意两个商品，考虑这两个商品同时具有的属性占它们所具有全部属性的比例，该比例越高，则这两个商品相似度越高；若该值高于相似度阈值ε，则在这两个商品对应节点之间存在一条无向边。下面给出基于对商品属性信息统计计算得到的用户间相似度计算方法，商品节点Oi和Oj的相似度用sim(Oi,Oj)表示：

其中，Bi⋂Bj描述两个商品同时具有的属性，N(Bi⋂Bj)表示属性个数；Bi⋃Bj表示两个商品共同具有的属性，N(Bi⋃Bj)为属性个数；N(Bi⋂Bj)和N(Bi⋃Bj)可基于简单的统计计算得到。

设ε为给定相似度阈值，当Oi和Oj的相似度sim(Oi,Oj)＞ε时，认为两个商品是相似的，即商品Oi和Oj对应节点之间存在一条无向边。

针对问题（2），考虑任意两个有边相连的节点，这两个商品的共同属性占各自属性的比例反映了它们的共同属性所占各自属性的比例，该比例值高的商品吸引的用户对于该比例值较低者也可能会感兴趣；基于此可确定相似关系的指向，从而确定图中边的方向。下面给出基于对商品属性信息统计计算来判断商品间指向关系的方法，商品Oi对Oj的依赖度用D(Oi|Oj)表示，商品Oj对Oi的依赖度用D(Oj|Oi)表示：

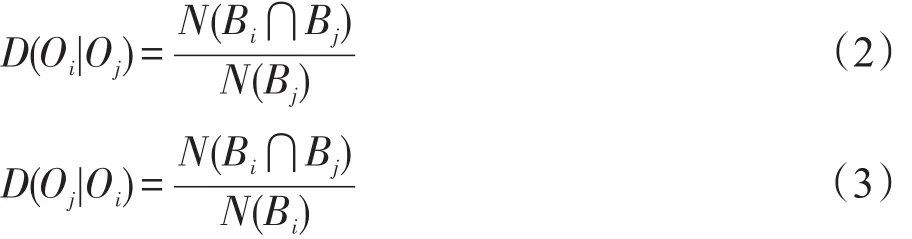
若D(Oi|Oj)＞D(Oj|Oi)，则表示Oi对Oj的依赖程度高于Oj对Oi的依赖程度，即Oj对Oi之间的有向边应由Oj指向Oi。

针对问题（3），首先建立一个已处理节点集合，用于存放处理后的节点。接着选取一个节点作为初始节点，分别通过相似性计算方法确定与其他节点之间的链接关系，当此链接关系指向的节点已有指向已处理集合中节点的边时，就忽略此链接关系，否则就保留此链接关系；处理完所有节点，就得到了目标结构。

算法1描述了上述思想。

算法1构建LBN的DAG

基于以上相似度和兴趣依赖度两个度量标准，可以得到LBN的DAG结构。然后，本文采用似然估计的方法[22]来计算贝叶斯网络中每个节点的概率参数表，从而最终得到LBN。

例4对于图1中KG，构建LBN的节点集Ol={M1, M2,M3}，其中S1={A1,A2,A3}，S2={D1,A3}，S3={A2,D2, A4}，再结合数据集D便可得到属性集。按照式（1），计算每两个电影节点之间的相似度，得到结果为sim(M1, M2)=0.66，sim(M1,M3)=0.35，sim(M3,M2)=0.54。假设ε的值预先设定为0.50，那么大于该值的两个节点之间应该有一条无向边。通过式（2）、式（3），计算每条边的方向，例如D(M2|M3)=0.42，D(M3|M2)=0.50，则两个节点之间的边应由节点M2指向节点M3。基于似然估计，计算各个节点的条件概率表CPT。最终得到的LBN如图2所示。

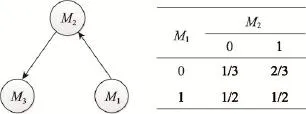
Fig.2 Asimple LBN图2 简单的LBN

4 基于LBN近似推理的KG链接预测

BN推理是指利用BN结构及其条件概率表，在给定证据后进行某些节点取值概率的计算。然而，BN的精确推理具有指数时间[23]。随着节点数的增加，推理的时间复杂度也会大幅度增加，尤其对于较大规模的KG而言，精确推理并不适用。因此，本文选择BN的近似推理算法。马尔科夫链蒙特卡罗算法[20-21]是目前被广泛应用的一种贝叶斯近似推理方法，Gibbs采样是MCMC方法中应用最广泛的一种。

本文基于Gibbs采样，利用已经和用户存在链接的商品节点作为证据节点，根据证据节点的取值来计算其他非证据节点在不同状态下的概率值。基于此计算用户和商品节点之间的边的可信度，作为KG链接预测的依据。为了便于计算，同时保证方法的普遍性，对于当前采样节点，本文仅考虑其马尔科夫覆盖（X的马尔科夫覆盖是包括X的直接孩子节点、直接父亲节点以及直接孩子其他父亲节点的节点集合，记为MB(X)）中的节点对它的影响[24]。算法2给出了具体的描述。

算法2基于Gibbs采样的LBN近似推理

利用算法2，可以得到 p(Oj=1|Oi=1)的值，即在给定证据变量Oi=1的情况下，非证据变量Oj=1的概率。由定义4可知，Oj的取值决定节点Oj与用户节点U之间是否存在链接。因此，p(Oj=1|Oi=1)的值为{Oi,U}已经存在的情况下{Oj,U}的可信度W。由上述可知，若W≥ε，则该链接真实存在。

例5对于图2中的LBN，{M2,U}已经存在，因此选择M2为证据节点，然后计算 p(M1=1|M2=1)，即{M1,U}的可信度。假设当前节点的状态是[M1=1,M2= 1,M3=0]。在当前状态下，通过M3马尔科夫覆盖中变量在当前状态下的值来对非证据节点M3进行采样，经过计算便可以得到p(M3=1|M1=1,M2=1)=1和p(M3=0|M1=1,M2=1)=0。假设生成的随机数r3=0.5，那么采样结果为M3=0，同时生成新的状态[M1= 1,M2=1,M3=0]。若采样次数为300，其中M1=1的次数为240，则p(M1=1|M2=1)=0.6，即未知链接{M1,U}的可信度为0.6。若ε=0.5，则该未知链接真实存在。

利用基于Gibbs采样的LBN推理算法，通过设定Ol中不同节点为非证据变量，可以依次获得该节点取值为1的概率，即该节点在Gk中与用户节点U之间未知链接的可信度，然后与给定阈值进行比较，则可判断该未知链接的真实存在性，从而发现用户和未存在链接商品之间是否存在关系。针对KG的链路预测，需要将真实存在的链接关系反映在KG的边上。对于描述用户兴趣的KG，若用户和商品之间存在关系，统一用“fondof”对其进行标注，实现用户兴趣KG中对于未知链接的预测。

5 实验结果

本文测试了LBN构建和LBN近似推理算法的效率以及KG链接预测的有效性。实验环境如下：Intel®CoreTMi5 2.40 GHz处理器，4 GB内存，Windows7操作系统，以Eclipse为开发平台，MySQL存储LBN的CPT，使用Java语言编写程序。实验中，针对形如图1的描述用户对电影兴趣的KG，将MovieLens站点数据与KG中原有数据结合，作为本文的测试数据。MovieLens数据集中包含6 040个用户对3 900部电影的1 000 209条评价数据，数据集格式为UserId：：MovieId：：Title：：Genres：：Rating，依次为用户Id、电影Id、电影名称、电影标签类型和电影评分，每个用户至少为20部电影评分，其中MovieId：：Title：：Genres构成了本文的外部数据集D。

5.1 LBN的构建效率

为了测试构建LBN算法的时间开销，选取包含10，20，…，100个节点的LBN，并分别测试了是否包含数据库I/O开销的LBN构建时间，如图3所示。可以看出，构建LBN的时间随着节点数的增加基本呈线性增长趋势。

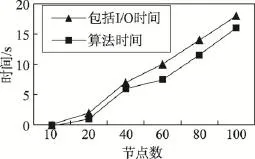
Fig.3 Efficiency of LBN construction图3 构建LBN的效率

5.2 LBN推理效率和收敛性测试

本文测试了基于Gibbs采样的LBN近似推理算法的效率。图4和图5分别给出了在不同节点数目情况下，随着采样次数的不断增加，算法2返回结果的收敛性和时间开销。从图4中可以看出，随着采样次数的增加，不同节点数目情形下LBN推理结果均能较快收敛到一个稳定的值（即静态分布），这从一定程度上说明了算法2的有效性。从图5中可以看出，不同节点数目情形下算法2的执行时间都随着采样时间呈线性趋势增加，这说明了LBN近似推理算法的高效性。

5.3 KG链接预测有效性测试

KG中的用户和商品节点之间的链接表示用户对于商品的偏好，因此通过判断预测用户偏好的准确性作为本文KG链接预测有效性的衡量标准。从MovieLens数据集中随机地选择某一个用户评分较高的5部电影，将其作为KG中的已知链接，再选取5部该用户未评过分的电影作为KG中的未知链接。给定预测阈值，高于阈值，则链接预测成功。为了测试基于LBN的概率推理进行KG链路预测方法的有效性，将已知边分为训练集和测试集两类。本文实验中，选择AUC（area under the receiver operating characteristic curve）、准确率（precision）和召回率（recall）作为衡量链接预测算法的指标。

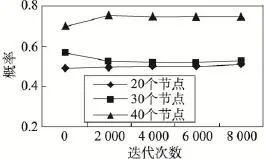
Fig.4 Convergence of LBN approximate inference图4 LBN近似推理结果的收敛性

Fig.5 Efficiency of LBN approximate inference图5 LBN近似推理算法的效率

实验中，测试不同迭代次数、不同训练集比例下3个指标的结果。从图6、图7和图8中可以看出，迭代次数的不同对于结果影响较小，而训练集比例的不同结果也会受到影响。对于AUC而言，AUC高于0.5的程度反映了算法在多大程度上比随机选择的方法精确[6]。由图6可以看出，在不同比例的训练集情况下，AUC的值都大于0.5，且随着训练集比例的增加，AUC的值不断增加。实验结果在一定程度上说明了本文提出的KG链路预测方法的有效性。

Fig.6 AUC of KG link prediction图6KG链路预测方法的AUC

Fig.7 Precision of KG link prediction图7 KG链路预测方法的准确率

Fig.8 Recall of KG link prediction图8 KG链路预测方法的召回率

同时，测试了不同迭代次数、不同训练集比例下的F值，如图9所示。F值综合了准确率和召回率，普遍在0.45以上，整体上说明了本文方法的准确性。

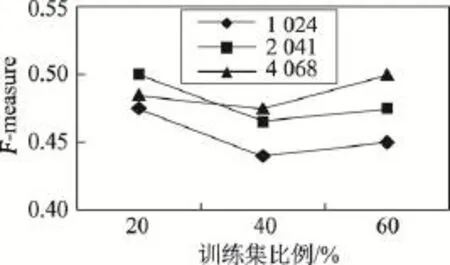
Fig.9 F-measure of KG link prediction图9KG链路预测方法的F值

综上，实验结果表明，本文基于LBN的KG链路预测方法在模型构建和链路预测方面都有较好的性能，也从一定程度上证明了本文方法的可行性。

6 总结与展望

本文以电子商务应用为背景，针对描述用户兴趣的KG，提出将KG与标签数据集结合，充分描述商品节点的属性，并构建了描述各属性间关联关系及其不确定性的LBN。然后基于BN的近似推理算法实现了对于未知链接不确定性的高效量化计算，从而发现KG中缺失的信息。通过建立在真实数据集上的实验，测试了本文方法的有效性，实验结果在一定程度上验证了所提出思路的可行性。

本文从用户和商品之间的关联度出发，为KG中未知链接的预测提供了一种新的思路，但仍是KG链路预测的初步探索。从KG链路预测问题的特点和应用来看，如何处理大规模的KG和海量的标签数据集，合理实现与现有思路的实验对比，将未知链路预测方法扩展到异常链路预测，是今后将要开展的工作。

[1]Wang Haofen.semantic search on large scale RDF data[D]. Shanghai:Shanghai Jiao Tong University,2013.

[2]Liu Qiao,Li Yang,Duan Hong,at el.Knowledge graph construction techniques[J].Journal of Computer Research and Development,2016,53(3):582-600.

[3]Doan A H,Madhavan J,Dhamankar R,et al.Learning to match ontologies on the semantic Web[J].The VLDB Journal,2003,12(4):303-319.

[4]Liu Ye,Zhu Weiheng,Pan Yan,et al.Multiple sources fusion for link prediction via low-rank and sparse matrix decomposition[J].Journal of Computer Research and Development,2015,52(2):423-436.

[5]Nickel M,Murphy K,Tresp V,et al.A review of relational machine learning for knowledge graphs[J].Proceedings of the IEEE,2016,104(1):11-33.

[6]Lv Linyuan,Zhou Tao.Link prediction in complex networks: a survey[J].Physica A:Statistical Mechanics and Its Applications,2011,390(6):1150-1170.

[7]Meng Xiaofeng,Du Zhijuan.Research on the big data fusion: issues and challenges[J].Journal of Computer Research and Development,2016,53(2):231-246.

[8]Bordes A,Gabrilovich E.Constructing and mining Web-scale knowledge graphs:KDD 2014 tutorial[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,New York,Aug 24-27, 2014.New York:ACM,2014:1967-1967.

[9]Dong Xin,Gabrilovich E,Heitz G,et al.Knowledge vault: a Web-scale approach to probabilistic knowledge fusion[C]// Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,New York,Aug 24-27,2014.New York:ACM,2014:601-610.

[10]Bollacker K,Evans C,Paritosh P,et al.Freebase:a collaboratively created graph database for structuring human knowledge[C]//Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data,Vancouver,Canada, Jun 9-12,2008.New York:ACM,2008:1247-1250.

[11]Getoor L,Diehl C P.Link mining:a survey[J].ACM SIGKDD Explorations Newsletter,2005,7(2):3-12.

[12]BordesA,Usunier N,Garcia-DuranA,et al.Translating embeddings for modeling multi-relational data[C]//Proceedings of the 27th Annual Conference on Neural Information Processing Systems,Lake Tahoe,USA,Dec 5-8,2013.Cambridge,USA:MIT Press,2013:2787-2795.

[13]Drumond L,Rendle S,Schmidt-Thieme L.Predicting RDF triples in incomplete knowledge bases with tensor factorization[C]//Proceedings of the 27th Annual ACM Symposium on Applied Computing,Trento,Italy,Mar 26-30,2012.New York:ACM,2012:326-331.

[14]Socher R,Chen D,Manning C D,et al.Reasoning with neural tensor networks for knowledge base completion[C]//Proceedings of the 27th Annual Conference on Neural Information Processing Systems,Lake Tahoe,USA,Dec 5-8,2013. Cambridge,USA:MIT Press,2013:926-934.

[15]Richardson M,Domingos P.Hybrid Markov logic networks [C]//Proceedings of the 23rd National Conference on Artificial Intelligence,Chicago,USA,Jul 13-17,2008.Menlo Park, USA:AAAI,2008:1106-1111.

[16]Heckerman D,Dan G,Chickering D M.Learning Bayesian networks:the combination of knowledge and statistical data [J].Machine Learning,1995,20(3):197-243.

[17]Koller D,Friedman N.Probabilistic graphical models:principles and techniques adaptive computation and machine learning[M]//Probabilistic Graphical Models:Principles and Techniques.Cambridge,USA:MIT Press,2009:161-168.

[18]Zhang Hongyi,Wang Liwei,Chen Yuxi.Research progressof probabilistic graphical models:a survery[J].Journal of Software,2013,24(11):2476-2497.

[19]Zhang Lianwen,Guo Haipeng.Introduction to Bayesian networks[M].Beijing:Science Press,2006.

[20]Mcculloch E,Variable selection via Gibbs sampling[J].Journal of theAmerican StatisticalAssociation,1993,88(423):881-889.

[21]Bayarri M J,Castellanos M E,Morales J.MCMC methods to approximate conditional predictive distributions[J].Computational Statistics&DataAnalysis,2015,51(2):621-640.

[22]Wang Tianren,Sayre E C.Maximum likelihood estimation (MLE)of students'understanding of vector subtraction[J]. American Institute of Physics Conference Series,2010,1289 (1):329-332.

[23]Pearl J.Probabilistic reasoning in intelligent systems[J].Computer ScienceArtificial Intelligence,1988,70(14):521-538.

[24]Zhu Zexuan,Ong Y S,Dash M.Markov blanket-embedded genetic algorithm for gene selection[J].Pattern Recognition,2007,40(11):3236-3248.

附中文参考文献：

[1]王昊奋.面向大规模RDF数据的语义搜索[D].上海:上海交通大学,2013.

[2]刘峤,李杨,段宏,等.知识图谱构建技术综述[J].计算机研究与发展,2016,53(3):582-600.

[4]刘冶,朱蔚恒,潘炎,等.基于低秩和稀疏矩阵分解的多源融合链接预测算法[J].计算机研究与发展,2015,52(2): 423-436.

[7]孟小峰,杜治娟.大数据融合研究:问题与挑战[J].计算机研究与发展,2016,53(2):231-246.

[18]张宏毅,王立威,陈瑜希.概率图模型研究进展综述[J].软件学报,2013,24(11):2476-2497.

[19]张连文,郭海鹏.贝叶斯网引论[M].北京:科学出版社,2006.

HAN Lu was born in 1990.He is an M.S.candidate at Yunnan University.His research interests include data analysis and knowledge discovery.

韩路（1990—），男，河北邯郸人，云南大学硕士研究生，主要研究领域为数据分析，知识发现。

YIN Zidu was born in 1990.He is a Ph.D.candidate at Yunnan University.His research interests include knowledge engineering,massive data analysis and services.

尹子都（1990—），男，甘肃天水人，云南大学博士研究生，主要研究领域为知识工程，海量数据分析与服务。

WANG Yujie was born in 1990.He is an M.S.candidate at Yunnan University.His research interests include knowledge engineering,massive data analysis and services.

王钰杰（1990—），男，河北唐山人，云南大学硕士研究生，主要研究领域为知识工程，海量数据分析与服务。

HU Kuang was born in 1982.He received the M.S.degree in software engineering from Yunnan University in 2009.Now he is a research associate at Information Technology Center,Yunnan University.He is working on Internet data center,and his research interest is container-based virtualization.

胡矿（1982—），男，云南楚雄人，2009年于云南大学软件工程专业获得硕士学位，现为云南大学信息技术中心助理研究员，主要从事数据中心建设工作，主要研究基于容器的虚拟化。

YUE Kun was born in 1979.He received the M.S.degree from Fudan University in 2004,and the Ph.D.degree from Yunnan University in 2009.Now he is a professor and Ph.D.supervisor at Yunnan University,and the member of CCF.His research interests include knowledge engineering,massive data analysis and services.

岳昆（1979—），男，云南曲靖人，2004年于复旦大学获得硕士学位，2009年于云南大学获得博士学位，现为云南大学教授、博士生导师，CCF会员，主要研究领域为知识工程，海量数据分析与服务。

Link Prediction of Knowledge Graph Based on Bayesian Network*

HAN Lu1,YIN Zidu1,WANG Yujie1,HU Kuang2,YUE Kun1+
1.School of Information Science and Engineering,Yunnan University,Kunming 650504,China
2.Information Technology Center,Yunnan University,Kunming 650504,China

+Corresponding author:E-mail:kyue@ynu.edu.cn

HAN Lu,YIN Zidu,WANG Yujie,et al.Link prediction of knowledge graph based on Bayesian network. Journal of Frontiers of Computer Science and Technology,2017,11(5)：742-751.

Link prediction is to discover and recover missing information in a knowledge graph(KG).Combining external knowledge and employing some specified methods to fulfill link prediction is the topic with great attention and key problem in KG research.Taking e-commerce application as the background,this paper combines the KG that has been constructed to describe user interest with external data,and adopts Bayesian network(BN),an important probabilistic graphical model,as the framework for representing and inferring the similarities among commodities as well as corresponding uncertainties.This paper constructs the BN to reflect the similarities by statistic computations upon commodity properties,and evaluates the authenticity of the links between commodity and user nodes based on the probabilistic inference mechanism of BN.Consequently,the real and complete KG can be obtained,as the basis of personalized recommendation and correlation query processing.The experimental results established onreal data show the effectiveness of the model and algorithms proposed in this paper.

knowledge graph;link prediction;Bayesian network;similarity;probabilistic inference

10.3778/j.issn.1673-9418.1608042

A

TP391

*The National Natural Science Foundation of China under Grant Nos.61472345,61562090,61402398(国家自然科学基金);the Applied Basic Research Project of Yunnan Province under Grant No.2014FA023(云南省应用基础研究计划);the Program for Innovative Research Team in Yunnan University under Grant No.XT412011(云南大学创新团队培育计划);the Program for Excellent Young Talents in Yunnan University under Grant No.WX173602(云南大学青年英才培养计划);the Innovative Research Foundation for Graduate Students of Yunnan University(云南大学研究生科研创新基金项目).

Received 2016-08,Accepted 2016-10.

CNKI网络优先出版:2016-10-31，http://www.cnki.net/kcms/detail/11.5602.TP.20161031.1650.012.html