双站阵列交叉定位系统误差控制优化

李国汉，孟晓军，修瑞云

(1.解放军69079部队，新疆 乌鲁木齐 830013；2. 解放军69029部队，新疆 乌鲁木齐 830013)



双站阵列交叉定位系统误差控制优化

李国汉1,2，孟晓军1，修瑞云1

(1.解放军69079部队，新疆 乌鲁木齐 830013；2. 解放军69029部队，新疆 乌鲁木齐 830013)

为了提高双站阵列交叉定位精度，提出了联合双站几何配置和阵列测向角度分析的方法，实现了几何精度因子(GDOP)条件下最小误差控制。理论分析和仿真表明，其定位精度取决于目标与测量站的相对几何位置、双站基线长度、阵列接收信噪比、阵元数、处理快拍数和阵列与双站基线夹角。双站配置应当根据重点监视和防范的空域来进行，阵列朝向应当正对重点威胁空域。

交叉定位；双站；几何精度因子；误差控制

0 引 言

双站交叉定位是无源定位技术的一种，由于双站交叉定位是一种准实时定位技术，因此在军事领域具有很大的应用潜力，特别是在对敌空中武器平台定位中，俄罗斯、美国等军事强国都有成功的应用。双站交叉定位利用几何关系通过计算进行定位，其定位精度与布站有密切关系。双站布站问题可以归纳为当目标位于某一位置时双站系统在何种条件下能够达到最佳的定位精度；更一般地，该问题可以表述为双站系统在何种条件下能够达到较好的定位精度。对于该问题，可以提高算法的定位性能，也可以改进双站的配置结构。目前定位精度分析大多限于几何位置带来的误差[1-2]，事实上不同的测向体制也会造成影响[3-4]。阵列测向是近年发展起来的高分辨率测向技术，对于低信噪比短时截获信号的定位具有独特优势。本文通过阵列测角误差定量分析测距误差，并以对美军数据链信号被动定位为例，联合分析阵列几何关系和阵列结构，提出控制双站阵列交叉定位误差的方法。

1 双站交叉定位系统数学模型

1.1 几何精度因子(GDOP)准则下最优配置

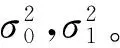
(1)

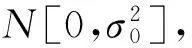
(2)

=tan(π-θ1)

(3)

或者：

=tanθ1

(4)

同理：

=tanθ0

(5)

那么：

(6)

同理：

(7)

(8)

其中：

(9)

估计方差为：

(10)

由此得到双站交叉定位下的几何分布误差：

(11)

(12)

得到：

(13)

(14)

式中：α为过S0,S1的直线与坐标横轴夹角。

如果把过S0,S1的直线作为坐标系的横轴，那么θ1+θ0=π，这表明当目标与两测量站构成等腰三角形时测量误差σGDOP最小。令x1-x0=L，把该约束关系代入GDOP函数有:

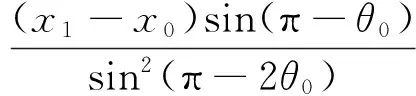
(15)

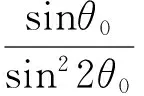
(16)

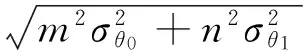
(17)

(18)

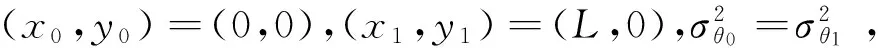
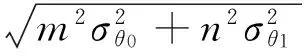
(19)

式中：θ为2站基线和目标所在的三角形顶角。

求导容易发现θ∈(0°,180°)时，只有1个极值点，且为极小值。基线长度值一定的条件下，目标离双站基线过近和过远都将导致定位误差的扩大。

1.2 阵列测向的角度误差

在上一节的模型中，未考虑到双站交叉定位时的测角误差，本节分析目标与阵列方向的相对位置对测角误差的影响。假设均匀直线阵列阵元间隔d，阵元数M，第一阵元为参考点并以此为坐标原点，考虑只有1个信号源S入射情况。各个阵元接收信号为xi(t)(i=0,1,…,M-1)，则:

xi(t)=ai(τi)s(t)+ni(t)

(20)

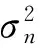
离散化为[5-6]：

(xi(0),xi(1),…,xi(N-1))=ai(Φ)(s(0),

s(1),…,s(N-1))+(n(0),n(1),…,n(N-1))

(21)

M个方程最终构成[6]：

x=a(Φ)⊗s+n

(22)

式中：⊗为直积；x的每一行为某一阵元的采样值，每一列为同一时刻各阵元采样值。

任意2行(m,n)采样相关函数：

(23)

(24)

那么，阵元接收数据协方差阵为：

(25)

而似然函数[4]为：

(26)

对于角度Φ估计[7]，克拉美-罗界C(Φ):

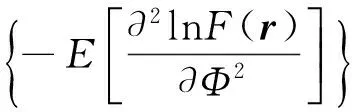
(27)

把R代入整理得到：

(28)

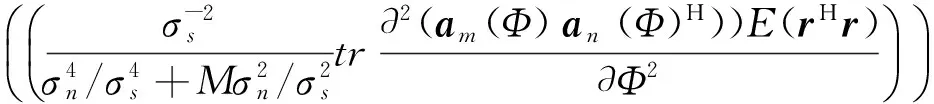
(29)

为进一步推导a(Φ)，如图2所示，设信号源到参考点距离为R，到第m阵元距离为Rm，那么根据三角形边和夹角关系:

(30)

Rm与信源参考点距离差为：

(31)

信源到第m个信元与到参考阵元时间差为：

(32)

任意2个阵元m,n时间差为：

(33)

到达方向(DOA)阵列估计一般情形是信号源为远场信号，R≫rm，式(33)后2项忽略，τmn有近似值：

(34)

ω=

(35)

代入式：

(36)

容易得到后面一项为零，那么上式简化为：

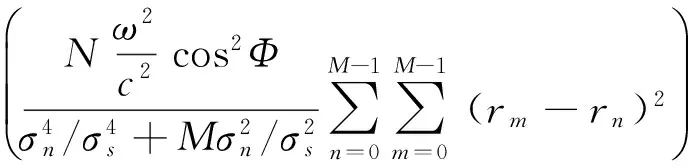
(37)

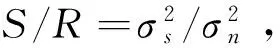
(38)

对于阵列测向体制，双站交叉定位存在最优几何配置解，在最优配置下定位精度存在下限，该下限与信噪比、阵元数量、阵元间距、方位角、信号频率和快拍数有关。考虑到测角误差，阵列交叉测向定位的最优配置是当阵列法向与最优角度重合时GDOP有最优解，具体配置如图3所示。

将式(38)代入式(19)，得到考虑阵列测角误差的最优配置GDOP误差下限为:

(39)

2 仿真比较

取某个联合战术信息分发系统(JTIDS)频点进行仿真，其中f=999 MHz,d=λ/2,M=4,N=2。取不同的信噪比进行仿真，如图4所示。在较低信噪比时，交叉定位误差迅速扩大。取信噪比为-10 dB，增加快拍数由2到50，仿真结果如图5所示。增加快拍数可以减少测量误差。取信噪比为-10 dB，快拍数2，改变阵元数，仿真结果如图6所示。可以看出，如果侦察环境处于低信噪比条件，可截获的快拍数较少，只能采取增大阵元数的方法来获得满意的定位误差。但增加阵元数会提高设备复杂度和运算复杂度，精度也不宜任意提高。

3 结束语

阵列交叉定位方法定位精度取决于目标与测量站的相对几何位置、双站基线长度、阵列接收信噪比、阵元数、处理快拍数和阵列与双站基线夹角。双站配置选址应当根据重点监视和防范的威胁空域来进行，阵列朝向应当正对重点威胁空域。本文对JTIDS信号阵列交叉定位测量站配置和阵列参数设计提供了有益参考。

[1] 叶映宇，文铁牛，陈俊，等.基于短波外辐射源的双站定位误差分析[J].现代雷达，2015(4):6-9.

[2] 王本才，何友，王国宏，等.双站无源均值定位算法精度分析[J].四川兵工学报,2010,31(4):78-81.

[3] 成先敏，李世中，乔晶晶，等.阵列信号处理中DOA估计的误差分析[J].科学技术与工程，2010,10(5):1153- 1155.

[4] 周宁.宽带源方位估计算法研究[D].开封：河南大学,2007.

[5] 由延军，黄建国，李雄.高分辨方位估计克拉美-罗界的改进算法[J].微处理机，2005(3):41-42.

[6] 刘云，李志舜.宽带波达方向估计的克拉美-罗界研究[J].声学学报，2006,31(2):126-131.

[7] TREES H L.Optimum Array Processing Part IV of Detection Estimation and Modulation Theory[M].New York:John Wiley Sons,Inc.,2002.

Error Control and Optimization of Dual-station Array Cross-location System

LI Guo-han1,2,MENG Xiao-jun1，XIU Rui-yun1

(1.Unit 69079 of PLA,Urumurqi 830013,China;2.Unit 69079 of PLA,Urumurqi 830013,China)

In order to improve the accuracy of dual-station array cross-location,this paper puts forward a method to perform combined bistatic geometric collocation and array direction-finding angle analysis,realizes the minimum error control under the condition of geometric dilution of precision (GDOP).Theoretic analysis and simulation indicate that the location accuracy is depend on the relative geometric position between target and measurement station,bistatic baseline length,signal and noise ratio of array reception,the number of array elements,the number of snapshots and the angle between array and dual-station baseline.Dual-station system should be configured in accordance with the important monitoried and protected airspace,the array orientation must be faced to the key threat airspace directly.

cross-location;dual-station;geometric dilution of precision;error control

cos3θ0-2sin2θ0cosθ0=0，θ0=35°

2016-07-08

TN971.1

A

CN32-1413(2017)02-0023-05

10.16426/j.cnki.jcdzdk.2017.02.006