基于遗传算法的机器人路径规划的仿真研究
雷艳敏,王 帅
(长春大学 电子信息工程学院,长春 130022)
基于遗传算法的机器人路径规划的仿真研究
雷艳敏,王 帅
(长春大学 电子信息工程学院,长春 130022)
鉴于其他传统机器人路径规划算法(如栅格法、人工势场法、A*算法等)存在搜索效率低、易于陷入局部最优解的问题,提出一种新的遗传算法。本文中将最短路径、避免碰撞(安全性能)和平滑度三者相结合作为新的适应度函数进行遗传优化,并给三个要素分配一定的权值。仿真结果表明:该算法搜索效率更高且能获得更好的路径规划结果。
遗传算法;适应度函数;路径规划
0 引言
在机器人研究领域中,路径规划是至关重要的。路径规划就是在有障碍物的环境中,按照某一性能指标(行走时间最短、路径最短或能量消耗最少等),为移动机器人规划出一条从起始点到目标点的最优或者近似最优的无碰撞路径[1]。机器人路径规划分为两种:一种是静态环境下的全局路径规划;另一种是动态环境下的局部路径规划。
机器人的路径规划有许多方法:如A*算法[2]、栅格法[3]、滚动窗口规划方法[4]、人工势场法[5]、神经网络法[6]和遗传算法等。每一种算法都有各自的优缺点,缺点主要有计算量大、搜索效率低、易陷入局部最优解等。为了提高算法的性能,对算法进行改进,主要包括算法本身的改进,或者把几种算法进行组合[7]。其中,遗传算法是一种全局寻优算法。由于具有鲁棒性、适应能力强的优点而得到了广泛的应用。为了提高遗传算法进行路径规划的安全性,并使规划的路径最短,本文提出一种新的适应度函数,该函数包含了最短路径、安全性和平滑度三个要素。最后通过仿真实验证明了该算法的可行性和有效性。
遗传算法首先要随机生成初始种群,然后用事先设定的评价标准适应度函数去筛选出优秀个体,之后优秀个体通过交叉、变异形成新的种群去优化目标函数,经过不断的迭代直到满足设定的算法终止条件为止,最终得到最优解[8]。
1 基于遗传算法的路径规划
1.1 环境建模
本文设定环境模型为二维结构化空间,障碍物在环境中的位置为Oi(xobs,i,yobs,i),将环境中设定的障碍物引入到初始种群的生成中。设置了检查装置,避免机器人经过的点或路径在障碍物内或边缘,防止陷入局部最优解。
1.2 适应度函数
适应度函数能有效地评价每条路径的优劣。适应度值的大小与路径的优劣成正比,因此,对遗传算法的收敛性和稳定性有着重要影响[9]。机器人路径规划的目的是使机器人从初始点到达目标点的运行路径最短并在行走的过程中无碰撞。因此,路径规划适应度函数的设计要满足三要素:机器人运行轨迹最短、运行过程中避开障碍物以及确保路径的平滑度。不与障碍物发生碰撞,是机器人在工作空间内行走的必要和基本条件。避免碰撞包括:任意路径点不能落在任何一个障碍物区域内及相邻两个路径点的连线与障碍物不相交。
1.2.1 最短路径
适应度函数的选取对于遗传算法来说很重要,适应度函数要能够快速计算每条路径长度。用公式(1)表示相邻两个路径点的长度:
(1)
公式(1) 中,(xi,yi)表示机器人的当前位置坐标,(xi-1,yi-1)表示机器人前一位置的坐标。则整条路径的长度可用公式(2)来计算:
(2)
公式(2)中,n为机器人的步数,因此,表示最短路径的适应度函数fit1为:
(3)
1.2.2 安全性能
对于遗传算法适应度函数的选取,除了要保证路径最短外,还要确保规划的机器人路径能安全行走(即无碰撞),则安全性能适应度函数fit2为:
(4)
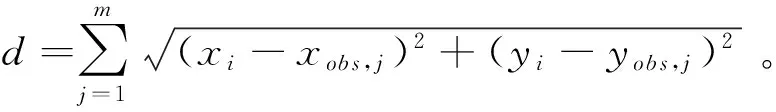
1.2.3 平滑度
机器人路径规划不仅要考虑到路径最短、避免碰撞,还要考虑到平滑度。本文利用余弦定理来解决平滑度问题,假设每个种群中每个线段的直线参数a、b、c(函数ax+by+c=0)。
公式(5)表示计算直线参数a:
(5)
公式(6)表示计算直线参数b:
(6)
公式(7)表示计算直线参数c:
(7)
公式(8)表示计算和值:
sumi=a2+b2-c2。
(8)
公式(9)表示计算总值:
(9)
则表示平滑度的适应度函数fit3为:
(10)
由公式(3)、公式(4)和公式(10)可知,用于表示移动机器人路径规划的最优适应度函数是:
fit=w1fit1+w2fit2+w3fit3。
(11)
其中w1、w2和w3分别为最短路径、安全性能和平滑度三个要素的加权系数。
2 仿真实验
Matlab是MathWorks公司的产品,是一个功能强大的数学软件,其优秀的数值计算能力使其在工业界和学术界的使用率非常高,所以,利用Matlab来编写遗传算法程序有着巨大优势。
2.1 设定初始数据
首先,建立环境模型,边界X轴Y轴都为20cm;设置障碍物个数为m=6;设定起始点坐标[0,0],目标点坐标[20,20];设定遗传算法种群规模为100;染色体长度为30;最大迭代次数为20代;种群变异率为0.01;种群交叉率为0.9。
2.2 仿真结果
2.2.1 最优适应度函数和平均适应度函数值变化趋势对比
在变异率pm=0.01,交叉率pc=0.9时,最优、平均函数值变化趋势如图1所示。从图中可以看出,在不断的迭代过程中,最优适应度函数值变化趋势趋于平稳,而平均适应度函数值始终保持不变。随着迭代次数的不断增加,最优适应度函数值不断地接近平均适应度函数值。当最优适应度函数值和平均适应度函数值相接近时,才能规划出理想中的路径。
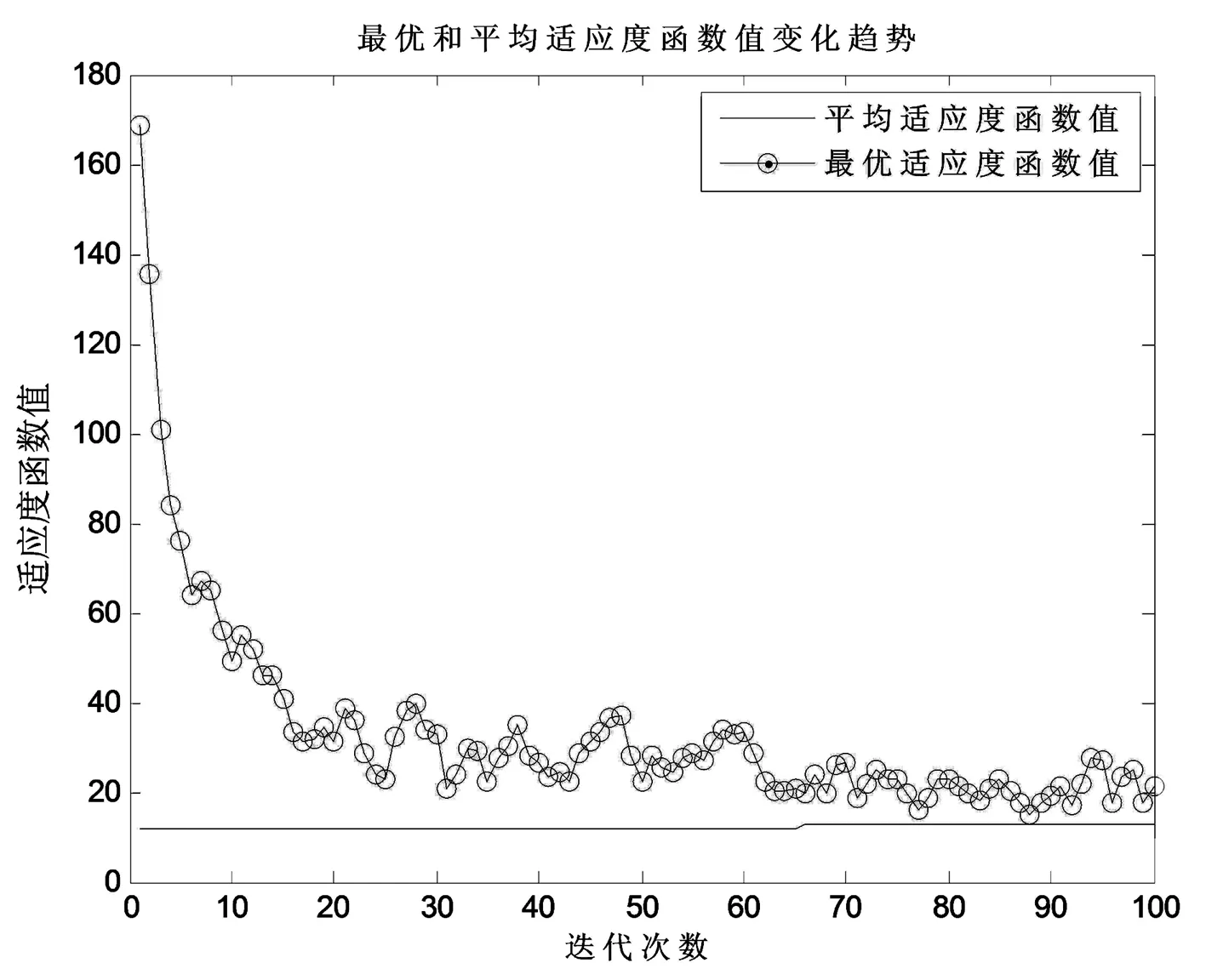
图1 最优和平均适应度函数值变化趋势
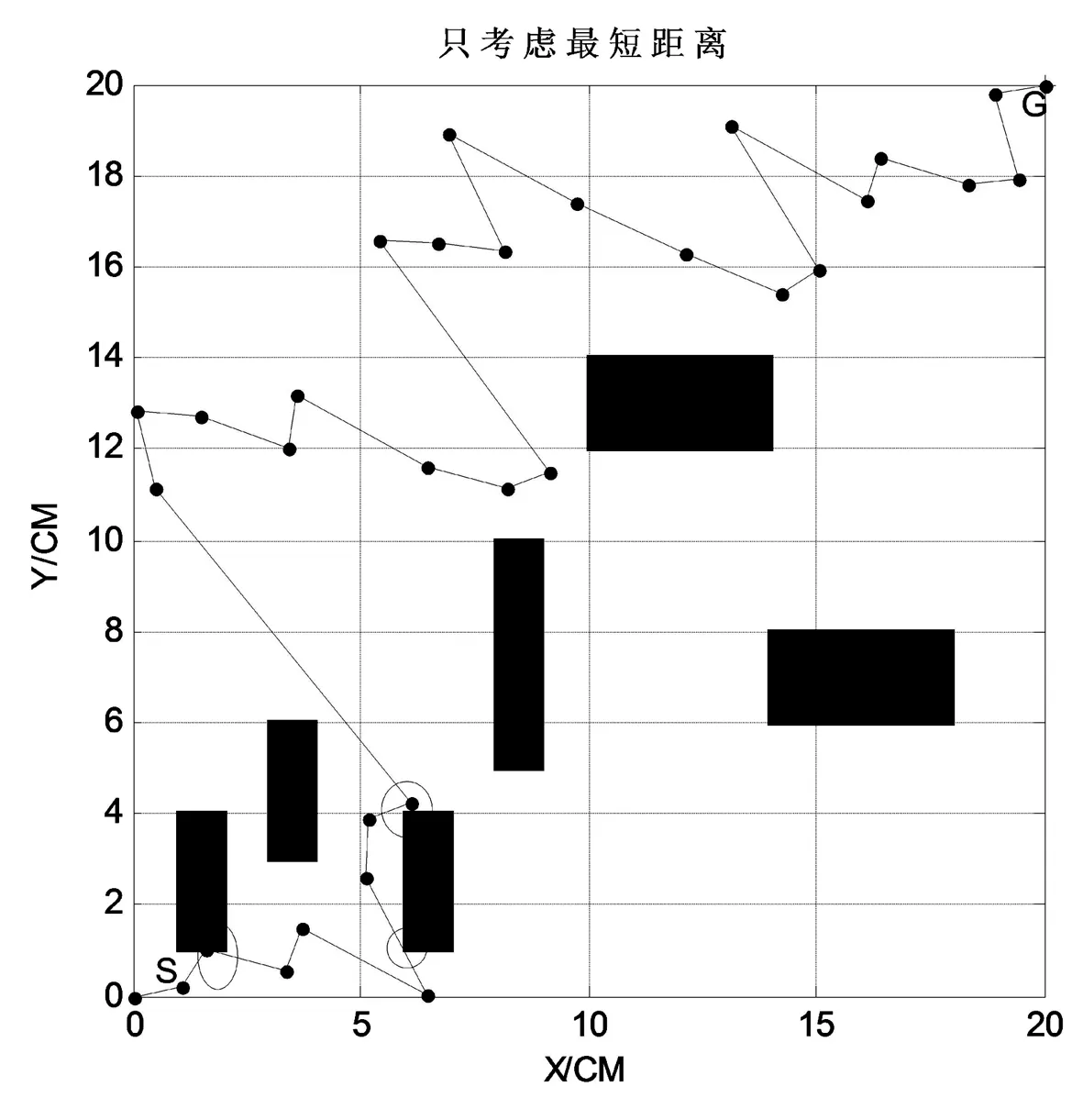
图2 只考虑最短路径的路径规划结果
2.2.2 路径规划实验结果
为了分析遗传算法中不同的适应度函数值对路径规划结果的影响,下面将分别对以下几种情况进行仿真。
(1)fit=fit1
fit=fit1,即只考虑机器人最短距离情况下路径规划,仿真结果如图2所示。从图中可以看出,只考虑最短距离的情况下,得到的并非是最优解,且如图中椭圆所标记的路径都无限地接近障碍物。因此,适应度函数只考虑路径最短是不全面的。
(2)fit=fit1+fit2
fit=fit1+fit2,即同时考虑最短距离与安全性能时的路径规划,仿真结果如图3所示。从图中可以看出,考虑到路径的安全性问题后,机器人在行进过程中明显避免了与障碍物发生碰撞的可能,但路径平滑度太差了。因此,在机器人路径规划中考虑最短距离与安全性能也是不全面的。

图3 考虑最短路径和安全性的路径规划结果

图4 考虑最短路径、安全性和平滑度的路径规划结果
(3)fit=fit1+fit2+fit3
fit=fit1+fit2+fit3,即综合考虑机器人最短距离、安全性能和平滑度情况下的路径规划,仿真结果如图4所示。从图中可以看出,综合考虑最短距离、安全性能和平滑度三个要素后基本上能够得到最优解,但规划出的路径并非完美。
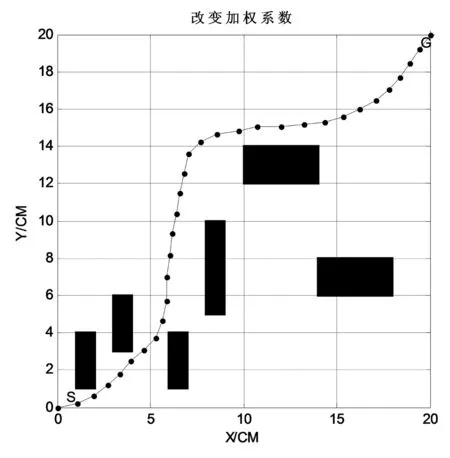
图5 改变适应度函数值时的路径规划结果
(4)fit=w1fit1+w2fit2+w3fit3
fit=w1fit1+w2fit2+w3fit3,即给最短路径、安全性和平滑度分配了一定的权值,使w1+w2+w3=1,加入权系数后可以得到完美的机器人路径,经过不断地实验验证得到当w1=0.4,w2=0.4,w3=0.2时规划的路径结果最好。
4 结论
本文在机器人路径规划问题的研究中,提出一种新的遗传算法。将最短路径、安全性能和平滑度三要素加入到适应度函数中,在存在障碍物的静态环境中,用该方法获得了最优路径。经过实验证明,通过多次迭代,最优适应度函数值变化趋于稳定,而且最优适应度函数值变化越小,寻找到的路径就越平滑。在适应度函数中加入权系数后,能获得更好的规划路径。但是,本文中适应度函数值中的权值是人为进行设置的,下一步将对权值的自寻优确定进行研究。
[1] 张毅,代恩灿,罗元. 基于改进遗传算法的移动机器人路径规划[J]. 计算机测量与控制,2016(1):313-316.
[2] 顾新艳,金世俊. 基于A*算法的移动机器人路径规划[J]. 科技信息(科学教研),2007(34):36-37+79.
[3] 王娟娟,曹凯. 基于栅格法的机器人路径规划[J]. 农业装备与车辆工程,2009(4):14-17.
[4] 孙斌,韩大鹏,韦庆. 基于滚动窗口算法的机器人路径规划应用研究[J]. 计算机仿真,2006(6):159-162.
[5] 赵荣齐. 基于人工势场法的机器人路径规划研究[D].济南:山东大学,2008.
[6] 黄磊. 基于神经网络的移动机器人路径规划研究[D].武汉:武汉理工大学,2008.
[7] 雷艳敏,冯志彬. 改进的势场栅格法在机器人路径规划中的应用[J]. 长春大学学报,2009,19(1):38-42.
[8] 巩敦卫,孙晓燕.协同进化遗传算法理论及应用[M].北京:科学出版社,2009.
[9] 石铁峰. 改进遗传算法在移动机器人路径规划中的应用[J]. 计算机仿真,2011(4):193-195+303.
责任编辑:程艳艳
SimulationStudyofRobotPathPlanningBasedonGeneticAlgorithm
LEIYanmin,WANGShuai
(CollegeofElectronicInformationEngineering,ChangchunUniversity,Changchun130022,Chine)
In view of the problems in other traditional robot path planning algorithms (such as grid method, artificial potential field method and A* algorithm etc.), including that the search efficiency is low and it is easy to fall into local optimal solution, this paper presents a new genetic algorithm, which makes a genetic optimization by combining the shortest path, avoidance of collision (safety performance) and smoothness as a new fitness function, and allocates a certain weight for the three elements. Simulation results show that the proposed algorithm is more efficient and can obtain better path planning results.
genetic algorithm; fitness function; path planning
2017-02-10
雷艳敏(1976-),女(满族),黑龙江五常人,副教授,博士,主要从事机器人智能控制及自动化控制方面的研究。
TP24
A
1009-3907(2017)04-0001-03

