利用智能算法优化支持向量机参数
崔君荣,苑薇薇
(沈阳理工大学 自动化与电气工程学院,辽宁 沈阳,110168)
利用智能算法优化支持向量机参数
崔君荣,苑薇薇*
(沈阳理工大学 自动化与电气工程学院,辽宁 沈阳,110168)
为了提高算法在实际问题中的应用能力,基于MATLAB仿真实验平台,研究了网格搜索算法、遗传算法和粒子群算法的参数优化方法,对支持向量机的惩罚因子和核函数参数进行优化处理,并利用标准的乳腺癌诊断数据集设计仿真实验。结果表明,利用智能算法优化支持向量机参数得到的分类精度比传统的根据经验选择参数的分类精度有了大幅度提高。
支持向量机;网格搜索算法;遗传算法;粒子群算法;参数优化
随着人工智能的发展,机器学习得到了越来越多的应用,机器学习主要研究计算机如何获取、发现所需要的知识,模拟和学习人类的行为,校正自我行为并利用已有经验优化自身性能。支持向量机(Support Vector Machine,SVM)是一种有监督的机器学习方法,在解决小样本、非线性及高维模式识别中表现出许多特有的优势[1]。支持向量机可以应用于入侵检测、故障诊断、模式识别、图像处理、数据挖掘等领域,因此建立一个泛化能力强的支持向量机模型尤为重要。
然而,SVM参数选取的好坏直接决定着支持向量机模型的优劣,传统支持向量机参数的选取一般是根据已有经验在一个区间内随机选取,容易引起过学习和欠学习问题,随机选取的参数偶然性比较大,对测试集合的准确率有很大的影响。关于SVM参数的选取优化,国际上也没有公认的最好的方法,因此对支持向量机参数优化的研究具有重要意义。
1 支持向量机参数的分析
支持向量机主要包括两大类:一类是支持向量分类机,另一类是支持向量回归机。对于支持向量机参数的选取对于这两大类具有相似的影响,因此可以平行应用[2]。本次主要基于支持向量机的分类机进行参数研究,支持向量机能否得到快速的发展,很大程度上取决于支持向量机参数的选取,对SVM影响比较大的参数主要是惩罚因子C和核函数参数g。
1.1 惩罚因子C
支持向量分类机的思想主要是通过输入向量从低维空间映射到高维空间,然后在高维空间构造最优分类面[3,4]。最优分类面问题又可以转化为如下的约束问题:
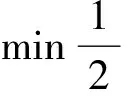
(1)
s.t.yi(wxi+b)-1≥0(i=1,2,…,l)
(2)
当训练集的数据集为线性不可分时,即两类数据有少量的交叉、融合,引入惩罚因子C和松弛变量ζ,松弛变量ζ表示舍弃距离最优分类面较近的线性不可分的数据所带来的损失,惩罚因子C表示对松弛变量引起的损失的重视程度。引入后最优分类面问题转化为如下约束问题[5,6]:
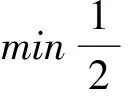
(3)
(4)
惩罚因子C值越大,表示越重视离群点。但是并不是C值越大越好,如果C值无穷大,需要满足的约束条件就越多,容易出现过拟合并且分类模型更复杂。如果C值越小,分类模型越简单但会出现欠拟合现象。惩罚因子C值过大过小都会导致模型泛化能力变差。因此,惩罚因子C的选择需要结合实际情况,在保证分类准确性的基础上尽量选取较小的C值得到简单的分类模型。
1.2 核函数参数g
现实生活中有大量数据之间的关系为非线性的,从低维空间映射到高维空间时映射关系及其复杂,针对此问题引入核函数。支持向量机使用核函数实现了在低维空间不可分的数据在高维空间线性可分[7],通过非线性变换将样本数据x映射到高维空间x‘,在高维空间设计线性可分算法,只需要知道样本数据x映射到高维空间后的x‘,将数据x和x‘做内积运算就可以实现低维空间中的非线性算法,甚至不需要知道映射关系,大大降低模型的复杂度。
选择不同的核函数就形成了不同的支持向量机算法[8],常用的核函数主要包括下面3类:
(1) 多项式核函数:
'
k(x,xi)=[(x,xi)+1]q
(5)
q为自由度,得到的是q维多项式分类器。
(2) 径向基函数(又称高斯核函数,RBF):
(6)
(3)Sigmoid函数:
k(x,xi)=tanh(v(x,xu)+c)
(7)
当高维空间维数很高时,多项式核函数q值很大,不仅计算量复杂而且也会影响分类的准确率。Sigmoid函数的应用也存在着一定的弊端,Sigmoid函数的参数只有部分值满足Mercer定理。径向基函数是应用最广的核函数,不仅适用于小样本和大样本,而且低维和高维也均适用,因此主要研究径向基函数的参数。
训练模型和测试模型的训练速度直接由支持向量的个数影响,核函数参数g越大,支持向量就越少,g值越小,支持向量就越多,但并不是g值越小越好,g值越小,测试模型的速度就会相对降低。
2 传统的参数选择方法
支持向量机的参数选择在国际上一直都没有公认最好的方法,传统的参数一般是根据经验进行选择。在[0,100]范围内进行参数C的选择,[-100,100]范围内进行参数g的选择,产生的C和g参数训练SVM,然后进行检测。结果表明,传统的根据经验随机选取参数的方法很难保证检测精度的理想效果(表1),虽然有时取到的参数也能得到较高的检测精度,但是随机性较大,也不能保证此时的参数是最优的。

表1 随机选取参数的检测结果
3 参数的优化方法
3.1 网格搜索算法
支持向量机网格搜索(Grid-Search,GS)的思想主要是针对惩罚因子C和核函数参数g设置搜索范围和步长[9],搜索范围确定了一个二维网格,假设M代表C的个数,N代表g的个数,以固定的步长在二维网格中搜索确定M*N个参数,将这些参数依次构建支持向量机训练模型,根据训练准确率确定最优参数C和g。若没有满意的参数则根据训练精度重新确定搜索范围和步长,直到确定最优参数[10]。
网格搜索算法是评估支持向量机分类准确率的方法之一。网格搜索算法可以并行搜索参数,并且搜索到M*N个参数是相互独立的,当参数较少时运算时间相对较低,但当参数较多时,例如D,E,F,G等4个参数,网格搜索后要处理D*E*F*G个参数,计算及其复杂。
3.2 基于遗传算法的参数优化
遗传算法(GeneticAlgorithm,GA)是模拟生物进化发展而来的优化算法,寻找支持向量机参数的最优值就是优化问题,并且遗传算法具有较强的实用性、高效性和鲁棒性,因此基于遗传算法对支持向量机进行参数优化是切实可行的[11,12]。遗传算法的基本思想主要如下:
Step1:将参数进行编码,得到种群染色体。
Step2:选择能表示个体优劣性的适应度。
Step3:对种群进行选择、交叉、变异,得到新种群。
Step4:对得到的新种群进行适应度评估,适应性强的个体保留,适应性差的个体淘汰。
Step5:重复进行step3和step4,直到满足预设的条件。
3.3 基于粒子群算法的参数优化
粒子群算法(ParticleSwarmOptimization,PSO)最早是从鸟类觅食得到启发形成的优化算法,鸟类捕获食物的最优路线就类似于粒子群算法所要求得的最优解[13,14]。粒子群算法中的每一个粒子都代表最优解集中的一个,主要由位置、速度和适应度来决定。
Vk+1=ωVK+c1r1(Pk-Xk)+c2r2(GK-XK)
(8)
Xk+1=XK+VK+1
(9)
其中, ω表示惯性权重;VK表示第k次迭代时的速度;c1和c2表示非负的加速度因子;PK是一个高维的列向量,表示个体极值;XK表示第K次迭代后的位置; GK表示所有粒子范围内全局极值点的位置。
利用公式(8)更新粒子的速度,利用公式(9)更新粒子的位置,选择合适的适应度公式计算粒子的适应度并提取粒子极值,重复更新粒子位置和速度,直到得到满足要求的极值。
3.4 智能算法对SVM的优化
通过以上3种算法分别对支持向量机参数进行优化,实验大体流程如下:
Step1:选取支持向量机的训练集和测试集。
Step2:对选取的数据进行预处理,去除噪声和冗余数据。
Step3:利用参数优化方法对参数进行优化,选取最优参数C和g。
Step4:对支持向量机进行训练,得到训练模型。
Step5:用测试集对训练模型进行验证,得到测试模型。
4 参数的优化实验分析
近年来,乳腺癌已成为危害女性健康的恶性肿瘤之一,发病率也呈明显上升趋势。因此,依据科学手段,对乳腺肿瘤良性和恶性的诊断具有重要的意义。本次优化实验分析的数据来源于威斯康辛大学医学院的乳腺癌数据集,共有569个病例,357个良性病例,212个恶性病例,标签“1”代表良性肿瘤,标签“2”代表恶性肿瘤,随机从中抽取500个病例作为训练数据,其余69个病例作为测试数据,选取不同的方法对支持向量机分类构造训练模型和测试模型,实验结果见图1~图6。
以上仿真实验对比表明,基于网格搜索算法的SVM分类得到的最优参数c=0.20,g=1.90,优化测试模型时间为0.700 607s,训练模型时间为6.608 805s(表2)。基于GA的SVM分类得到的最优参数c=0.81,g=0.86,优化测试模型时间为0.709 723s,训练模型时间为3.974 219s。基于PSO的SVM分类得到的最优参数c=1.69,g=0.39,优化测试模型时间为0.135 633s,训练模型时间为3.352 519s。
对表2分析,基于网格搜索算法的SVM分类对训练数据的检测精度较高,对测试数据分类稍差,当参数较多时利用网格搜索的运算量巨大,检测时间较长。基于遗传算法的SVM分类对测试数据具有较强的检测能力,对检测函数要求不是很高,但是实时操作较复杂,需要针对不同问题调整交叉变异等算子。基于粒子群算法的SVM分类对测试数据检测精度稍差,粒子群算法主要的缺点是容易陷入局部最优,但对训练数据检测精度较高,且检测时间大大缩短。
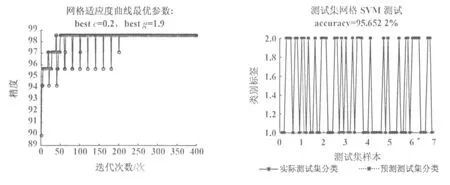
图1 网格搜索得到的最优参数 图2 基于网格搜索的SVM分类
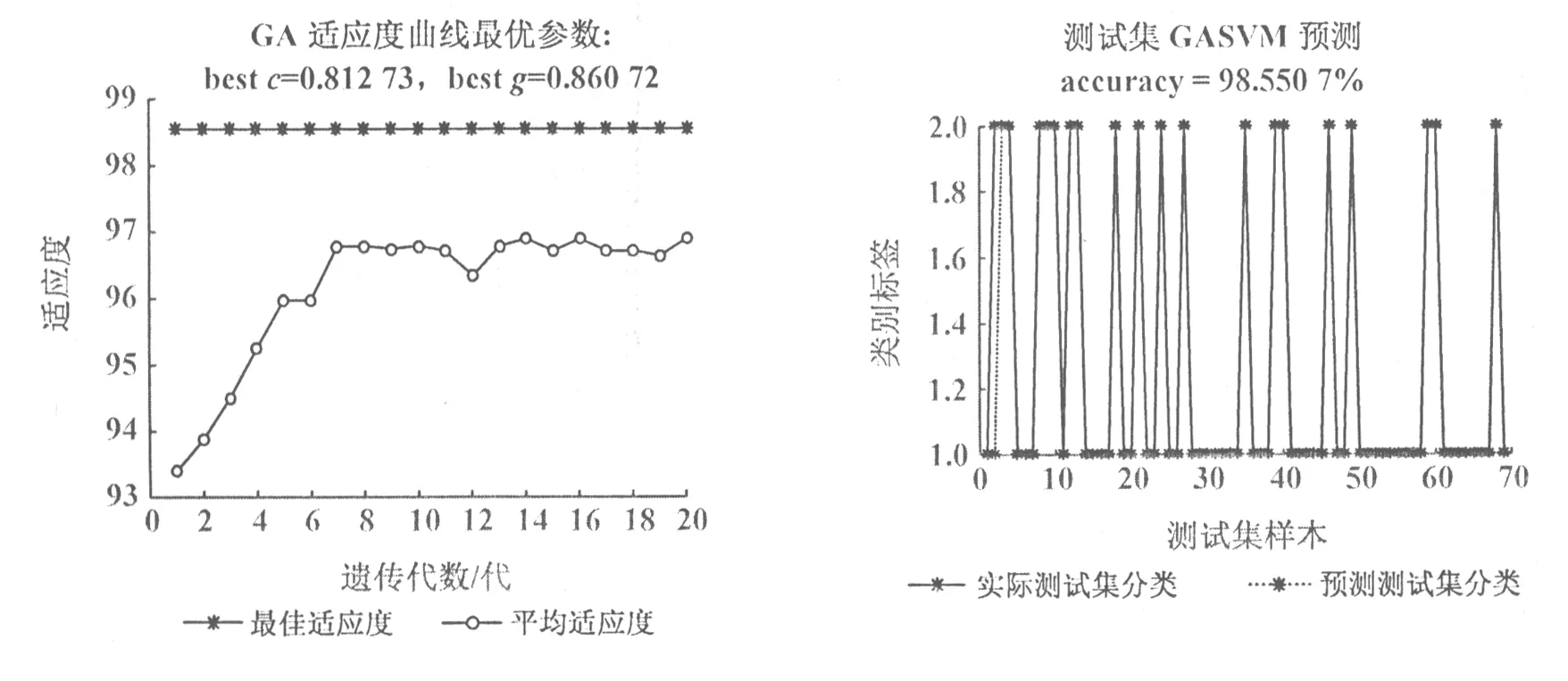
图3 GA得到的最优参数 图4 基于GA的SVM分类
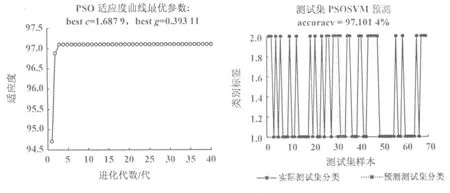
图5 PSO得到的最优参数 图6 基于PSO的SVM分类
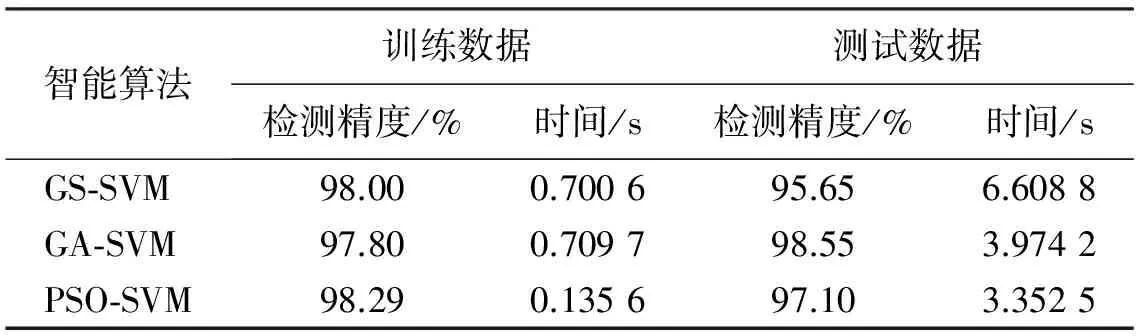
表2 智能算法优化支持向量机参数实验结果
5 结 论
通过网格搜索算法、遗传算法、粒子群算法分别对支持向量机的参数进行了优化,建立了3种训练模型,对matlab实验仿真结果的检测精度和训练时间比较分析,总结了3种智能算法优化支持向量机参数的优缺点,利用智能算法优化支持向量机参数的检测精度更高,比传统的根据经验选择的参数得到的结果更稳定,智能算法优化参数后的SVM在故障诊断、入侵检测等领域具有更好的应用效果。
[1] 李娇.支持向量机参数优化研究[D].武汉:华中师范大学,2011.
[2] 张楠.关于支持向量机中的参数优化的研究[D].西安:西北大学,2008.
[3] 魏峻.一种有效的支持向量机参数优化算法[J].计算机技术与发展,2015,25(12):97-104.
[4] 肖永良,朱韶平,刘文彬,等.基于优化支持向量机的高校教师绩效评价研究[J].赤峰学院学报(自然科学版),2014,24:25-27.
[5] 尚丹.基于参数优化的SVM分类器在肺癌早期诊断中的应用[D].郑州:郑州大学,2014.
[6] 徐晓明.SVM参数寻优及其在分类中的应用[D].大连:大连海事大学,2014.
[7] 冯新刚.支持向量机核函数选择方法探讨[D].赣州:江西理工大学,2012.
[8] 梁礼明,钟震,陈召阳.支持向量机核函数选择研究与仿真[J].计算机工程与科学,2015,37(6):1 135-1 141.
[9] 亢生彩.网格搜索法SVM参数优化在主扇风机故障诊断中的应用[J].煤炭技术,2015,34(1):295-297.
[10] 万飞.基于网格搜索的支持向量机在入侵检测中的应用[D].合肥:合肥工业大学,2015.
[11] Kuang F J,Xu W H,Zhang S Y.A novel hybrid KPCA and SVM with GA model for intrusion detection[J].Applied Soft Computing,2014,18(5):178-184.
[12] 刘东平,单甘霖,张岐龙,等.基于改进遗传算法的支持向量机参数优化[J].微计算机应用,2010,31(5):11-15.
[13] Subasi A.Classification of EMG signals using PSO optimized SVM for diagnosis of neuromuscular disorders[J].Computers in Biology and Medicine,2013,43(5):576-586.
[14] 张俊才,张静.使用粒子群算法进行特征选择及对支持向量机参数的优化[J].微电子学与计算机,2012,29(7):138-141.
(责任编辑:朱宝昌)
Optimization of Support Vector Machine Parameters Based on Intelligent Algorithm
CUI Junrong,YUAN Weiwei
(School of Automation and Electrical Engineering, Shenyang Ligong University,Shenyang Liaoning, 110168, China)
Parameter selection plays an important role in the algorithm of support vector machine (SVM) data processing performance. In order to improve the application ability of the algorithm in practical problems, the parameter optimization methods of grid search algorithm, genetic algorithm and particle swarm optimization algorithm were compared based on MATLAB simulation experiment platform. The penalty factor and kernel function parameters of SVM were optimized, and a simulation experiment using the standard breast cancer diagnosis data set was designed. The results showed that the classification accuracy of SVM parameters based on intelligent algorithm was better than that of the traditional method.
support vector machine; grid search algorithm; genetic algorithm; particle swarm optimization; parameter optimization
10.3969/J.ISSN.1672-7983.2017.01.007
2016-12-08; 修改稿收到日期: 2017-01-10
TP301.6
A
1672-7983(2017)01-0034-05
崔君荣(1991-),女,硕士研究生。主要研究方向:机器学习、工业控制入侵检测。
*通讯作者,女,副教授,硕士研究生导师。主要研究方向:机器学习、复杂系统故障诊断与监控技术。E-mail:yww131@126.com。

