带交叉扩散项的捕食模型正稳态解的存在性分析
黄喜娇 1,李景荣 2
(1 安阳学院,河南 安阳,455000;2 河南科技大学附属高级中学)
带交叉扩散项的捕食模型正稳态解的存在性分析
黄喜娇 1,李景荣 2
(1 安阳学院,河南 安阳,455000;2 河南科技大学附属高级中学)
讨论了一类具有交叉扩散项的Holling-Tanner捕食-食饵生态模型的正稳态解的存在性。利用最大值原理给出了此模型正解的先验估计,进一步利用特征值和单特征值的局部分歧理论,以物种v的增长率b作为分歧参数,证明了系统在半平凡解附近出现分歧。
交叉扩散项;Holling-Tanner捕食-食饵模型;先验估计;分歧解
研究了一类具有扩散和交叉扩散项的模型:
(1)
其中u,v分别代表捕食和食饵者的密度; Ω是RN(N≥1)中具有光滑边界∂Ω的有界区域; ∂v表示单位外法向量的方向导数;边界条件表示它们生活在同一个封闭的环境,参数a,b 是 u,v的固有增长率; γ表示捕食者依赖食饵者的程度; m是食饵者的饱和值。 d1,d2为交叉扩散系数,并且对应的 d1描述食饵者避开大群捕食者来避免侵害的趋向,对应的 d2描述食饵者聚在一起抵制来自捕食者的侵害的趋向,上述的参数 d1,d2是非负数,其他都是正的。
对于一些捕食模型,国内外已有许多研究,并且取得了许多有意义的成果,诸如捕食问题正稳态解的存在性、稳定性和局部分歧以及捕食模型解的渐进性研究[1~9]。在这些文献中,多数讨论的是不带交叉扩散项的模型,也即是(1)模型中 d1,d2=0时的情形。如PengR等[8]研究了相应的不带交叉扩散项模型平衡态非常数正解的存在与不存在性,PengR等[9]讨论了正解的一些性质,笔者在此基础上讨论(1)的平衡态模型
(2)
(3)
因为a>0,显然问题(3)有唯一一个正解,记为θa,因此模型(2)有一个半平凡解,记为(ω*, v*) ,则(u*, v*)=(θa, 0)。
本次研究用 λ1(q)表示下面问题的主要特征值。
(4)
1 模型(2)解的先验估计
假设在模型(2)中d1, d2≠0,为了讨论的方便,令ω=(1+d1v)u, χ=(1+d2u)v, 那么可得
(5)
显然(u,v)>0与(ω,χ)>0是一一对应的,那么模型(2)又可写为下面形式
(6)
其中u=u(ω,χ), v=v(ω,χ)是由(5)给出的关于ω,x的函数,易知(6)也有一个半平凡解记为(ω*, χ*),则(ω*, χ*)=(θa,0)。
为了给出模型(2)正解的估计,先介绍引理1。
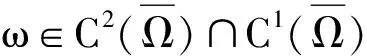

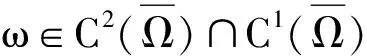

定理1 假设 (ω, χ)是模型(6)的正解, (u,v)是模型(2)的正解,那么
0 0 u(x0)≤a,v(x0)≤a(m+a) 因此 0 那么 又 v也是正解,所以 0 在此以 b作为分歧参数,其它参数固定,讨论模型(2)在半平凡解(θa,0)附近的正解。对系统 (7) 为了讨论模型(2)在半平凡解(θa,0)的某邻域存在正解,先介绍引理2。 引理2 L1的所有特征值均是负的,其中L1=Δ+a-2θa。 定理2 因a>λ1,模型(2)在半平凡解(θa,0)的某邻域内存在正解。 由于模型(6)与模型(2)是等价的,下面证明模型(6)在半平凡解(θa,0)的某邻域内存在正解,从而得出模型(2)在半平凡解(θa,0)的某邻域内存在正解。 (8) (9) 定义映射F:X×R→Y则(8)式的左端为 (10) 所以可知F(0,0,b)=0,从(9)和(10)知F在(0,0,b) 的导Fre'chet导数是 所以有 所以 (u(s),v(s),b(s))是模型(2)的解,其中 u(s),v(s)是由(5)给出的关于 w(s), χ(s)的函数。易见,当 0 本次研究了一类具有交叉扩散项的Holling-Tanner捕食-食饵生态模型。主要讨论了此模型的正解。利用最大值原理给出了此模型正解的先验估计,进一步利用特征值和单特征值的局部分歧理论,讨论了模型正解的存在性。 [1] Wollkind D J,Collings J B,Logan J A.Metastability in a temperature-dependent model system for prey-predator mite outbreak interactions on fruit flies[J].Bulletin of Mathematical Biology,1988,50:379-409. [2] Braza P A.The bifurcation structure of the Holling-Tanner modle for prey-predator interactions using two-timing[J].J Appl Math,2003,63:889-904. [3] Collings J B.Bifurcation and stability analysis of a temperature-dependent mite prey-predator interactions model incorporation a prey refuge[J].Bulletin of Mathematical Biology,1995,57:63-76. [4] 李景荣,李艳玲,闫焱.一类带交叉扩散项的捕食模型正解的存在性[J].陕西师范大学学报(自然科学版),2009,37(1):20-24. [5] 谢君辉,雷森文.一类带扩散的捕食者-食饵模型解的性态研究[J].湖北民族学院学报(自然科学版),2014,32(4):398-401. [6] 孙玉涛,常郝,张子振,徐勇.一类时滞食饵-捕食者系统的稳定性研究[J].赤峰学院学报(自然科学版),2014,30(8):7-8. [7] 谢君辉,刘婷婷,孙涛.一类具反应扩散的捕食模型平衡态模式的定性分[J].湖北民族学院学报(自然科学版),2015,33(3):247-251. [8] Peng R,Wang M X.Positive Steady-states of the Holling-tanner Prey-predator Model with Diffusion[J].Proc Roy Soc Edinburgh A,2005,135(1):149-164. [9] Peng R,Wang M X.Global stability of the equilibrium of a diffusive Holling-Tanner prey-predator model[J].Appl Math Lett,2007,20(6):664-670. [10] Crandall M G,Rabinowitz P H.Bifurcation from simple eigenvalues[J].Journal of Functional Analysis, 1971,8(2):321-340. [11] Lou Y, Ni W M.Diffusion,self-diffusion and cross-diffusion[J].Journal of Differential Equations,1996,131(l):79-131. [12] Wu J H.Global bifurcation of coexistence state for the competition model in the chemostat[J].Nonlinear Analysis,2000,39(7):817-835. [13] Smoller J.Shock waves and reaction-diffusion equations[M].New York:Springer-Verlag,1983. (责任编辑:朱宝昌) Existence of Positive Steady-state Solution for a Prey-Predator Model with Cross-Diffusion HUANG Xijiao1, LI Jingrong2 (1 Anyang University, Anyang Henan,455000; 2 Senior High School Affiliated To Henan University of Science And Technology; China) The existence of positive steady-state solution for a prey-predator model with cross-diffusion was discussed in this paper.The prior estimate to the positive solutions of the model was given by means of maximum principle. Furthermore, treating the increase ratebas the bifurcation parameter, the bifurcation from the semi-trivial solutions was obtained according to the local bifurcation theory with eigenvalues. cross-diffusion; Holling-Tanner prey-predator model;prior estimate; bifurcation solution 10.3969/J.ISSN.1672-7983.2017.01.006 河南省高等学校重点科研资助项目(项目编号:17A110015)。 2016-10-12; 修改稿收到日期: 2017-03-02 O175.26 A 1672-7983(2017)01-0029-05 黄喜娇(1980-),女,硕士,讲师。主要研究方向:微分方程。
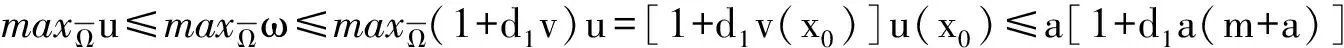

2 模型(2)正解的存在性

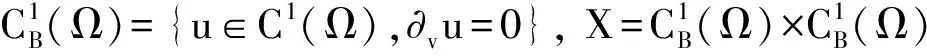



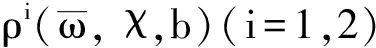
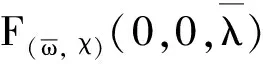




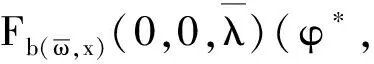


3 结 论

