带漂移布朗运动的一个局部时的Laplace变换

吴婵,陈晔

(1.长沙理工大学 数学与统计学院,湖南 长沙,410114;2.湖南文理学院 数学与计算科学学院,湖南 常德,415000)

带漂移布朗运动的一个局部时的Laplace变换

吴婵1,陈晔2

(1.长沙理工大学 数学与统计学院,湖南 长沙,410114;2.湖南文理学院 数学与计算科学学院,湖南 常德,415000)

在Borodin和Salminen(2002)文献中有关带漂移布朗运动占位时的Laplace变换结果的基础上,运用Li等(2014)计算局部时的方法,推出了带漂移布朗运动在独立指数时间eq前,及停留在0处的局部时的Laplace变换表达式。当μ=0时,本文结果与标准布朗运动的结果吻合。

局部时;Laplace变换;带漂移的布朗运动

局部时和占位时是随机过程理论研究的2个热点问题,它们在风险理论和金融模型中有广泛应用。占位时是随机过程在一个特定区间内逗留的时间总和,而局部时是其相关的占位密度。计算占位时的Laplace变换的表达式主要有3种方法,经典的方法是通过Feynman-Kac公式[1-2]得到过程对应的随机微分方程,从而得到相应的占位时的Laplace变换的表达式[3]。Landriault等[4-5]采用了逼近占位时的方法并结合游弋理论,得到了谱负Lévy过程的占位时Laplace变换[6]。为了克服随机过程路径的无变差性,Li和Zhou[7]首次运用泊松过程的性质,将计算谱负Lévy过程的联合占位时的Laplace变换问题转化为求某个随机事件的概率问题[8]。目前,对随机过程的局部时的Laplace变换的研究还比较少。

本文在文献[9]的有关带漂移布朗运动在随机指数时间eq之前,停留在区间(0,a)上的占位时表达式的基础上,运用文献[10]中求局部时的方法,通过对过程占位时的 Laplace变换求极限,得到过程停留在0处的局部时的Laplace变换表达式。本文得到了局部时的Laplace变换表达式。

1 预备知识

设Xt=μt+Wt是带漂移布朗运动[9],其中漂移系数μ∈ R,Wt是一维标准布朗运动。带漂移布朗运动在独立指数时间eq之前,停留在区间(0,a)上占位时的Laplace变换表达式[9]为

其中,eq是强度为q的指数随机变量,与过程X独立,且

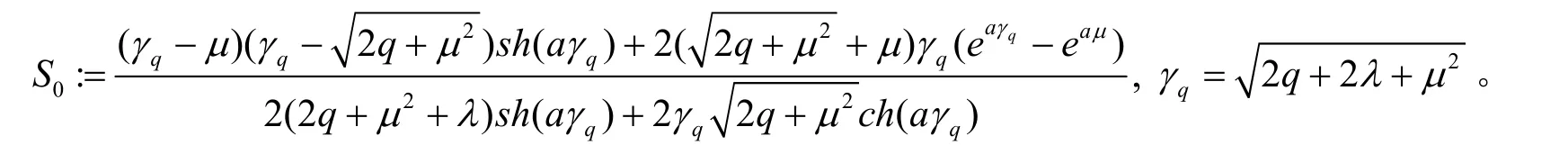
2 主要结果

运用文献[10]中求局部时的方法,通过对带漂移布朗运动占位时的 Laplace变换表达式取极限,得到局部时的Laplace变换表达式。

[1]Pitman J,Yor M.Laplace transforms related to excursions of a one-dimensional diffusion [J].Bernoulli,1999:249-255.

[2]Pitman J,Yor M.Hitting,occupation and inverse local times of one-dimensional diffusions:martingale and excursion approaches [J].Bernoulli,2003,9:1-24.

[3]Cai N,Chen N,Wan X.Occupation times of jump-diffusion processes with double exponential jumps and the pricing of options [J].Math Oper Res,2010,35:412-437.

[4]Asmussen S,Taksar M.Controlled diffusion models for optimal dividend payout [J].Insur Math Econ,1997,20:1-15.

[5]Landriault D,Renaud J F,Zhou X.Occupation times of spectrally negative Lévy processes with applications [J].Stochastic Process Appl,2011,121:2 629-2 641.

[6]Li Y,Wang S,Zhou X,et al.Diffusion occupation time before exiting [J].Front Math China,2014,9:843-861.

[7]Li Y,Zhou X.On pre-exit joint occupation times for spectrally negative Lévy processes [J].Stat Probab Lett,2014,94:48-55.

[8]Chen Y,Yang X,Li Y,et al.A joint Laplace transforms for diffusion for pre-exit diffusion of occupation times [J].Acta Math,2016:1-17.

[9]Borodin,A N,Salminen P.Handbook of Brownian Motion-Facts and Formulae [M].2nd edition.Basel:Birkhäuser Verlag,2002:261-262.

[10]Li Y,Zhou X,Zhu N.Two-sided discounted potential measures for spectrally negative Lévy processes [J].Stat Probab Lett,2015,100:67-76.

(责任编校:刘刚毅)

Laplace transform of one local time on brownian motion with drift

Wu Chan1,Chen Ye2
(1.College of Mathematics and Statistics,Changsha University of Science and Technology,Changsha 410114,China;2.College of Mathematics and Computational Science,Hunan University of Arts and Science,Changde 415000,China)

On the basis of the results in Borodin and Salminen(2002),the approach in Li et al.(2014)is adopted to consider the local time at 0 before independent exponential timeeq,and the Laplace transform of local time on Brownian motion with drift is obtained.The result is.Whenμ=0,the result consists with classical result of Brownian motion.

local time;Laplace transform;brownian motion with drift

O 211.6

A

1672-6146(2017)02-0009-03

吴婵,1003011369@qq.com。

2017-01-20

国家自然科学基金(11571052,11171044);湖南省自然科学基金(2016JJ4061);湖南省研究生科研创新项目(CX2016B417);湖南文理学院科学研究项目(15ZD05)。

10.3969/j.issn.1672-6146.2017.02.003