给定分支点数目树的离心率总和
江玲瑶,汤自凯
(湖南师范大学 数学与计算机科学学院,湖南 长沙,410081)
给定分支点数目树的离心率总和
江玲瑶,汤自凯
(湖南师范大学 数学与计算机科学学院,湖南 长沙,410081)
设G=(V,E)是简单连通图,简单连通图G的离心率总和定义为图G中所有顶点的离心率总和。若树T中某个顶点的度大于等于 3,则称这个点为T的分支点。刻画了给定分支点数为r顶点数为n的树的离心率总和的上界和下界。
离心率总和;分支点;树;极值图
ζ指数是用来描述分子结构特征的最经典的拓扑指数之一,它在物理化学建模[1−5]和生物研究[6−8]中都有很多应用。Dankelmann等[9]介绍了一个基于距离的拓扑指数,这个指数被称为离心率的总和,它的定义是
若树T中某个顶点的度大于等于3,则称这个点为T的分支点。当树至少有一个分支点和至多有r≤n/2− 1个分支点时,树的特征是不一样的。林洪[10]研究了分支点数目对 Wiener指数的影响,刻画了n个顶点r个分支点树的Wiener指数的上界和下界。因此,本文将刻画分支点数目是怎样影响离心率总和及n个顶点r个分支点树的离心率总和的上界和下界。
1 术语和符号说明
设G=(V,E)是简单连通图,V(G)和E(G)分别为图G的顶点集与边集,记为图G的阶或记为n,为图G的边数或记为(或d(v))为顶点v在图中G的度,对于u,v∈V(G),在G中顶点u,v之间的最短路的长度称为这两个点的距离d(u,v),点v到其他顶点最大的距离为v的离心率ε(v)。若一个点的度为1,则称这个点为悬挂点,如果点v0为悬挂点,则路为G中一条悬挂路,其中内部顶点的度为2,vk的度至少为3。设Sn,Pn为n个顶点的星图和路。对于其他的专业术语和符号均参考文献[11]。
2 主要结论
引理1 设u为图G0(至少有2个顶点)中的1个顶点。对整数a≥1,将Sa+1的中心和u连接得到G1。将u连接a+1个悬挂点得到G2,则

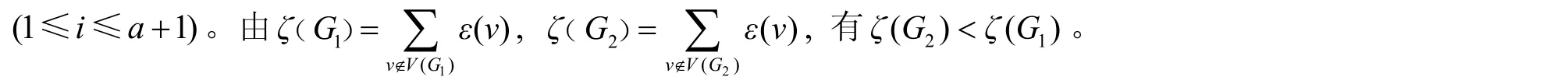

图1 引理1的图
引理 2 设w为非平凡连通图G的一顶点,对于非负整数p和q。设为由G中顶点w连接长度为p和q的悬挂路和如果则

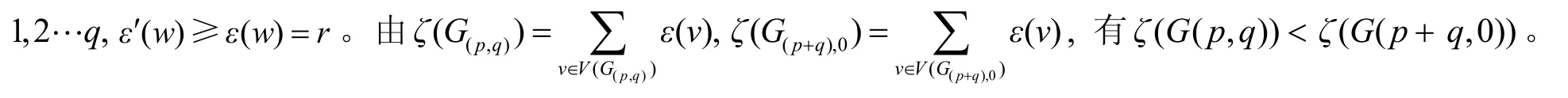
由引理1和引理2易得如下结论。
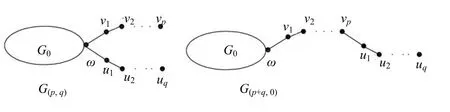
图2 引理2的图
定理1 在n个顶点的树中,Sn的离心率总和最小,nP的离心率总和最大。接下来,给出给定分支点数目的n个顶点树的离心率总和的上界和下界。
设ΒΤn,r为n个顶点r个分支点的树的集合。F(n,r)和B(n,r)如图3所示。显然,
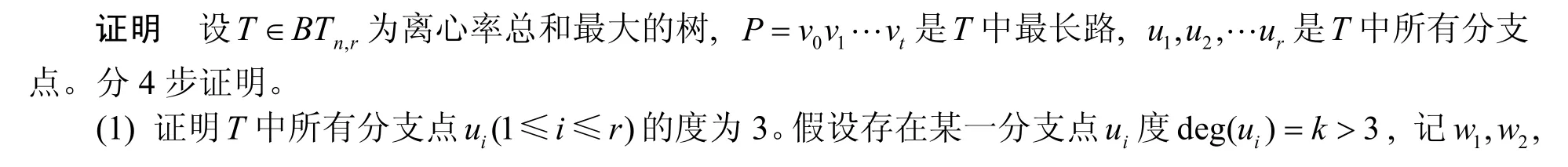
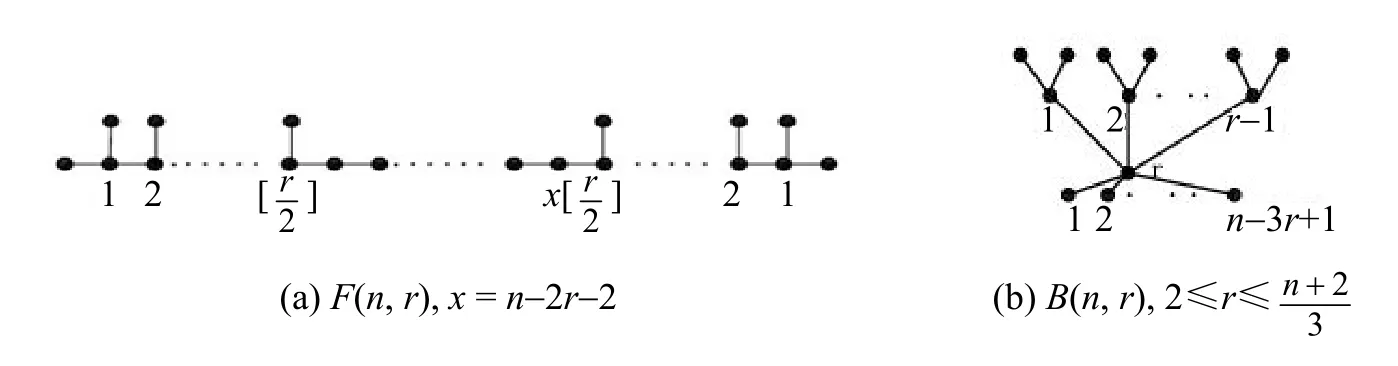
图3F(n,r)和B(n,r)


图4 定理2证明(2)的图



[1]Arezoomand M,Taeri B.Applications of generalized hierarchical product of graphs in computing the Szeged index of chemical graphs [J].MATCH Commun Math Comput Chem,2010,64:591−602.
[2]De N.Augmented eccentric connectivity index of some thorn graphs [J].Int J Appl Math Res,2012,1(4):671−680.
[3]Eliasi M,Taeri B.Four new sums of graphs and their Wiener indices [J].Discret Appl Math,2009,157:794−803.
[4]Eskender B,Vumar E.Eccentric connectivity index and eccentric distance sum of some graph operations [J].Trans Comb,2013,2(1):103−111.
[5]Fathalikhani K,Faramarzi H,Youse-Azari H.Total eccentricity of some graph oper-ations [J].Electron Notes Discret Math,2014,45:125−131.
[6]Gutman I.Distance in thorny graph [J].Publ Inst Math,1998,63:31−36.
[7]Metsidik M,Zhang W,Duan F.Hyper and reverse Wiener indices of F-sums of graphs [J].Discret Appl Math,2010,158:1 433−1 440.
[8]Tang Y,Zhou B.On average eccentricity.MATCH Commun [J].Math Comput Chem,2012,67:405−423.
[9]Dankelmann P,Goddard W,Swart C S.The average eccentricity of a graph and its Subgraphs [J].Util Math,2004,65:41−51.
[10]Lin H.On the Wiener index of trees with given number of branching vertices [J].MATCH Commun Math Comput Chem,2014,72(1):301−310.
[11]Bondy J A,Murty U S R.Graph theory with applications [M].London:Macmillan,1976.
(责任编校:刘晓霞)
On the total eccentricity of trees with given number of branching vertices
Jiang Lingyao,Tang Zikai
(College of Mathematics and Computer Science,Hunan Normal University,Changsha 410081,China)
LetG=(V,E)be a simple connected graph,the total eccentricity of a simple and connected graphGis defined as the sum of eccentricities of all vertices inG.Avertex of a treeTwith 3 or greater is called a branching vertex ofT.That the upper bound and the lower bound of the total eccentricity of an n-vertex tree with r branching vertices are determined.
the total eccentricity;the branching vertex;tree;extremal graph
O 157.5
A
1672-6146(2017)02-0005-04
汤自凯,zikaitang@163.com。
2016−11−10
项目资助:湖南师范大学优秀青年项目(ET13101)。
10.3969/j.issn.1672-6146.2017.02.002

