对数线性模型的选择方法及其应用

戴建国

(广州大学 数学与信息科学学院,广东 广州,510006)

对数线性模型的选择方法及其应用

戴建国

(广州大学 数学与信息科学学院,广东 广州,510006)

为构造最佳对数线性模型,通过λ系数构造λ相关系数矩阵,将其作为对数线性模型中交互项选择的方法,并用于分析肺癌治疗数据。结果表明,选出的交互项可以构造最佳的模型对数据进行准确的分析,因此在应用对数线性模型分析前,先用相关系数矩阵进行探索性研究分析是很有必要的。

对数线性模型;相关系数矩阵;交互项

对数线性模型是处理非线性相关离散数据常用的一种分析方法[1],而分类离散数据通常以列联表的形式呈现,在医疗数据和社会调查数据中尤为常见。列联表有二维、三维或者更高维的形式,其表达的是多个分类变量交叉计数的资料,对数线性模型是处理这类数据的有效工具。对数线性模型分为饱和模型、条件独立模型、部分条件独立模型、相互独立模型(即只含主效应)[2]。对于最简单的二维列联表,其由2个属性变量构成,分别表示成行和列,具有2个主效应和1个交互效应。对于三维或者更高维的情况,主效应增加,交互效应也随之增加,这时就需要选择有用的效应构造合适的模型。之前也有一些文献讨论过对数线性模型的选择方法,如:张岩波等[3]利用了 Brown’s偏关联检验筛选模型;崔静等[4]通过自适应 Lasso对对数线性模型中的变量进行选择;李春红等[5]探讨了 Adaptive elastic net方法在Poisson对数线性模型选择中应用;唐先勇[6]将3维列联表中所有可能的HLLM模型分成2大类,然后运用AIC准则从接受类中挑选出“最佳”模型。

本文以3维列联表为例,引入λ系数,并构造λ相关系数矩阵对交互效应进行选择,通过拟合优度统计量和BIC、AIC准则[1-7]对模型进行评价。

1λ系数

λ系数是Leo A Goodman与William H Kruskal在1954年提出来的[8],其基本原理是假定有2离散变量X、Y分别有I和J个类别,可构成2维联合分布,对样本中个体进行随机选择,将一半分配到Y变量上,另一半分配到X变量上。按照相对减少误差比例的规则对变量作出预测,在未知另一个变量的情况下,猜Y变量类别时,猜测个体最有可能出现在π+M类别上,即Y边缘概率最大的那一类,猜对的概率为π+M/2。同理,猜测X变量时,猜测个体最有可能出现在πM+类别上,猜对的概率为πM+/2(M为最大行列边缘概率对应的行与列),则总的猜错概率为 1−(πM++π+M)/2;而在已知另一半的情况下进行猜测时,猜测Y变量最好的预测是(其中m表示在给定行列下最大联合概率对应的列与行),即X每个类别下Y最大概率的总和的一半,猜测X变量最好的预测是即Y每个类别下X最大概率的总和的一半,因此猜错总概率为则相对减少误差比例。其中π表示频率,n表示频数。下面举例说明,数据联合分布见表1。其中X有3个类别,Y有3个类别。即X、Y的λ相关系数为0.152 8。当有多个变量时,各变量间的λ系数则可构造λ相关矩阵。

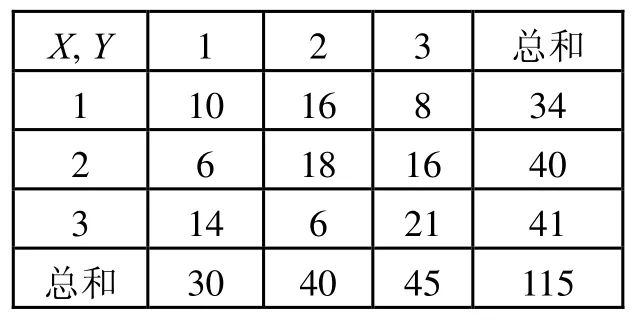
表1 简单的二维列联表

2 三维列联表的对数线性模型

设一个3维列联表有X、Y、Z3个属性变量,Xi、Yj、Zk(i=1,2,…,R;j=1,2,…,C;k=1,2,…,T)分别表示各属性变量的类别,期望频数mijk=E(nijk)。3维列联表的所有对数线性模型如表2所示。

表2 3维列联表的各类模型

在模型表达式中:μ是指总平均;为X在i时的主效应;为相应的主效应;为Xi与Yi的二次交互效应;为相应的二次效应;为三次交互效应。

表3 小细胞肺癌实验数据

3 应用实例

在一项治疗小细胞肺癌的试验中,患者被随机地分成2组。连续治疗组在每一个治疗周期使用相同的化学药物联合疗法,交替治疗组在不同治疗周期使用不同的药物组合,分析不同性别,治疗组的疗效有无差别。3个属性变量分别记为X、Y、Z,数据[9]见表3。通过R软件计算三者的λ相关系数矩阵如表4所示。从λ相关系数矩阵来看,Y、Z存在交互关系,另外2对变量关系几乎为0,所以模型中只要考虑Y、Z交互效应。表5给出了所有可能的对数线性模型,以及相应的似然比拟合优度统计量、皮尔森卡方拟合优度统计量、自由度、p值以及BIC、AIC的值。

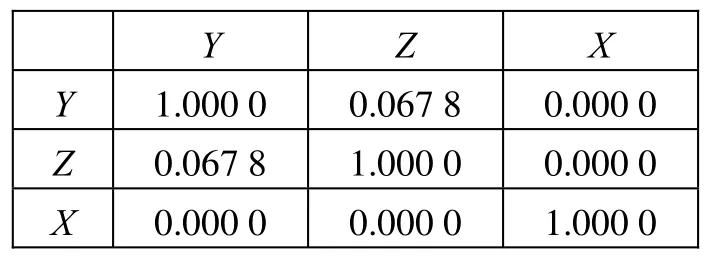
表4λ相关系数矩阵

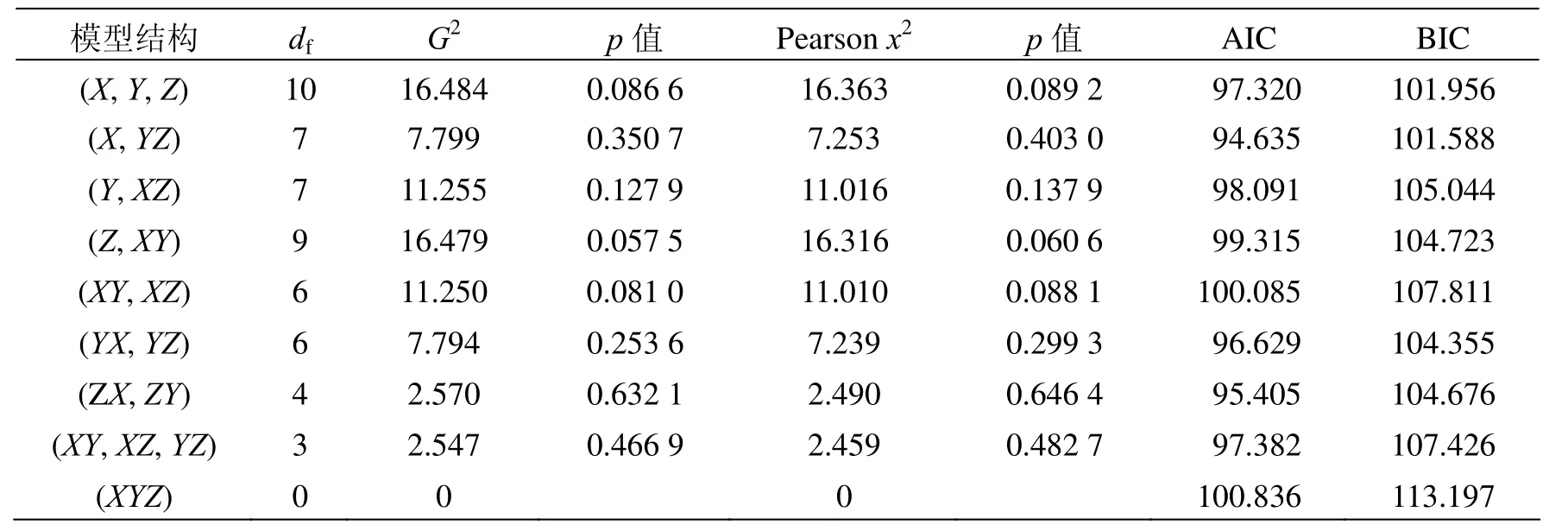
表5 各种对数线性模型拟合结果

由表5可知,简单模型(X,YZ)的AIC、BIC值最小,分别为94.635、101.588,并且拟合优度统计量的p值均接受原假设。虽然模型(YX,YZ)、(ZX,ZY)、(XY,XZ,YZ)拟合优度统计量的p值均接受原假设,但其比模型(X,YZ)更为复杂,并且AIC、BIC准则值均比模型(X,YZ)的值大,从而不宜作为最佳模型。而对于饱和模型一般没有多大意义,因为该模型的参数个数和列联表单元格一样多。这说明选(X,YZ)作为最佳模型是合理的,与用λ相关系数矩阵选出的结果完全一样,即性别对疗效几乎无影响,主要是受到治疗方式的影响。

4 总结

通过λ相关系数构造了相关系数矩阵,其可作为探索性研究分析的有工具,使得各变量间的关系一目了然,因此在进行构造对数线性模型前,可以先通过λ相关矩阵进行分析,找出变量间的关系,选择合适的交互项假如对数线性模型。这样可以为选择最优的对数线性模型提供有力的依据,提高模型的预测能力。除此之外,还可构造一种与文献[10]类似特征选取的算法,但有待进一步研究。

[1]Alan Agresti.An Introduction to Categorical Data Analysis [M].New York:Wiley-Interscience,2007.

[2]赵平.定性数据的统计分析[M].北京:社会科学文献出版社,2014:75-78.

[3]张岩波,何大卫.对数线性模型的最优模型筛选策略[J].中国卫生统计,1996,13(6):4-7.

[4]崔静,郭鹏江,夏志明.自适应Lasso在Poisson对数线性回归模型下的性质[J].西北大学学报(自然科学版),2011,41(4):565-568.

[5]李春红,黄登香,覃朝勇.一种改进的 Lasso方法及其在对数线性模型中的应用[J].广西大学学报(自然科学版),2015,40(3):758-765.

[6]唐先勇.3维列联表中对数线性模型的选择策略[J].湖南科技学院学报,2003,1(1):155-159.

[7]Edwards D,Abreu G C D,Labouriau R.Selecting high-dimensional mixed graphical models using minimal AIC or BIC forests [J].BMC Bioinformatics,2010,11(1):158-180.

[8]Goodman L A,Kruskal W H.Measures of Association for Cross Classification [J].Journal of the American Statistical Association,1954,49:742-744.

[9]胡良平.SAS统计分析教程[M].北京:电子工业出版社,2010:162-163.

[10]胡佩姗,孙吉康,王平.基于改进最小冗余最大相关及私有化预测用于抗菌肽活性的QSAR研究[J].湖南文理学院学报(自然科学版),2016,28(1):29-34.

(责任编校:刘刚毅)

Logarithmic linear model selection method and its application

Dai Jianguo
(Mathematics and Information Science Department,Guangzhou University,Guangzhou 510006,China)

In order to construct the best logarithm linear model,that making the coefficient of correlation coefficient matrix as interaction item selection of a logarithmic linear model is used to analyze the lung cancer treatment data.Results show that the interaction item which had selected can construct the best model,the analysis of the data is accurate,so before the application of logarithmic linear model analysis,correlation coefficient matrix analysis of exploratory research is necessary.

logarithm linear model;the correlation coefficient matrix;interactive items

O 212.1

A

1672-6146(2017)02-0021-03

戴建国,1012894435@qq.com。

2017-02-18

10.3969/j.issn.1672-6146.2017.02.006