浅析换元法在中学数学中的应用

江苏省盱眙县第一中学 徐 升

浅析换元法在中学数学中的应用

江苏省盱眙县第一中学 徐 升

一、换元法相关概念及几种常见的换元法

1.换元法的相关概念

所谓换元法，又称辅助元素法、变量代换法，即把某个式子看成一个整体，用一个变量去代替它。

换元的实质是转化，它是用一种变数形式去取代另一种变数形式，使问题得到简化。利用换元法解数学题的关键在于适当地选择“新元”，引进适当的代换，找到较容易的解题思路。换元法的基本思想是通过变量代换，使原问题化繁为简、化难为易，使问题发生有利的转化，从而达到解题目的换元法的一般步骤：

2.几种常见的换元法

（1）均值换元法

在某些问题中，已知两未知量的和，这时将这两个未知量用它们的均值和一个新的变量来表示，从而使计算化繁为简，这就是均值换元法。例如，当

纵观上述两例可以看出，均值换元法实质上是换元思想的一种具体运用，它利用了两个量的平均值和一个字母，沟通了原来两个量之间的关系，能够简便计算，在解题中有着广泛的应用。

（2）常值换元法

所谓常值换元法，就是将题目中的常数用字母表示，将其他数字转化为相应的字母，这种方法能使问题的本质特征显现出来，从而有助于寻找解题思路，简化解题过程。

分析：本题若直接求解，显然比较困难，观察其数字特征，联想其一般情形，可将1987用一个字母a表示，则1986可表示为a-1问题得到简化。

（3）比值换元法

所谓比值换元法是指当式子中出现恒等的分式，且每个分式都含有未知数时，由于这些未知数之间存在一定的关系但又不太好表示，因此我们可引进一个新的未知数使之等于上述恒等式，然后用这个新的未知数表示原来的各未知数。

（4）增量换元法

当一变量在一常量附近变化时，可设这一变量为该常量加上另一个变量，这种方法叫作增量换元法。

（5）三角换元法

三角代换也是常用的一种换元方法，在解某些代数问题时，选用适当的三角函数进行换元，把代数问题转化为三角问题，充分利用三角函数的性质去解决问题，常能使问题易于解决，这种方法叫三角换元法。如在解有关的无理不等式和方程时，如果我们直接将无理式有理化后求解，则必须平方，这样势必要对其进行讨论，过程烦琐，若我们能对问题的特征进行分析，借助三角换元，则可使问题化难为易，简捷获解。例如当问题中含有形如的无理式时，常令

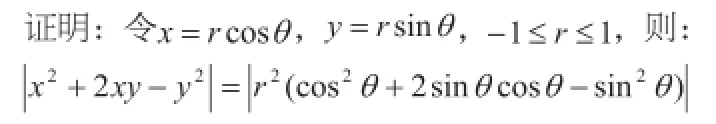
（6）对称换元法

当题目中的未知数具有对称关系时，可应用基本对称式进行代换，使解题过程简化，这种方法称为对称换元法。

二、换元法在解方程中的应用

1.换元法在双二次方程中的应用

在中学课程中要求学生会解一些特殊的高次方程，有时我们会碰到“双二次方程”，即只含有未知数的四次项、二次项和常数项的方程。对于这类方程，可以经过对二次项的换元转化为一元二次方程。

思路2：把方程展开成标准的双二次方程，再对x2进行换元。

注意：换元的关键是善于发现或构造方程中表达形式相同的部分作为换元的对象。在解方程的过程中，换元的方法常常不是唯一的，解高次方程时，只要能达到降次目的的换元方法都可以应用。

2.换元法在无理方程中的应用

解无理方程时，常把原方程中的一个含有未知数的根式作为整体进行换元，达到去根号转化为可解方程的目的。这时经过变形，原方程的某个整式部分常可表示为新元的平方。

解：原方程可化为：

注：以前学过平方去根号法解无理方程，是一种普遍方法。现在的换元法必须构造出根号内外两个相同的式子才行。

3.换元法在分式方程中的应用

解分式方程时，常把原方程中的一个分式作为整体进行换元，换元时要注意分子、分母互换的两个分式可以用一个新元和它的倒数来表示。例如方程可变形为进行换元得去分母后化为可解。

分析：如果分式方程中满足两个分式互为倒数关系（如解方程：这时，只需设其中一个分式为辅助元即可；如果含有未知数的各个分式的分母都是关于未知数的二次三项式，且二次项系数和一次项系数对应成比例（如解方程这时，只需设二次项系数的绝对值最小的多项式为辅助元即可。

解：原方程可化为：

注：对于分式方程或无理方程使用换元法后，仍需对所求根进行检验。

4.换元法在解方程组中的应用

在构成方程组的方程里，有关未知数的代数式呈对称性，换元法可借此特点使方程组简单化，便于求出方程组的解。

解：由（1）得：

通过以上所有例子可以看出 ，在初等数学中，换元法的确有着极其重要的作用。学会运用换元法，不但可以沟通数学各个分支之间的联系，还可以扩大视野，培养学生的学习兴趣。对于一些较难的题目，我们还应当通过认真观察问题的结构特征，深入分析问题的隐含条件，采用类比、联想猜测等手段进行适当的换元，并综合运用各方面的知识给予解决。

book=70,ebook=72