中国50th人体小腿有限元模型多工况优化建模方法

张冠军 王龙亮 邓小朋 杜现平 官凤娇

1(湖南大学汽车车身先进设计制造国家重点实验室，长沙 410082)2(国防科学技术大学装备综合保障技术重点实验室, 长沙 410073)

中国50th人体小腿有限元模型多工况优化建模方法

张冠军1王龙亮1邓小朋1杜现平1官凤娇2*

1(湖南大学汽车车身先进设计制造国家重点实验室，长沙 410082)2(国防科学技术大学装备综合保障技术重点实验室, 长沙 410073)

人体下肢是交通事故中最易受伤的部位之一，下肢有限元模型则成为研究下肢损伤机理和防护方法的重要工具，而要保证模型生物逼真度则需开展多工况全面验证。人体模型验证所需的生物力学试验数据由于样本尺寸、材料等多样性造成力学响应存在差异，难于用一个模型同时满足多个试验数据。中国人体与欧美人体在几何尺寸上的差异会造成生物力学响应的不同，因此有必要开发中国人体的有限元模型。通过CT、MRI扫描建立小腿几何模型，利用由胫骨关键尺寸确定的缩放系数，将小腿几何模型缩放至中国50百分位人体小腿。同样采用缩放方法，将生物力学试验数据缩放至小腿尺寸所对应的生物力学响应数据，以解决试验样本几何差异的影响。以胫骨和腓骨的弹性模量、应力-应变曲线、失效应变以及肉体体积模量为设计变量，采用优化方法，同时拟合胫骨和腓骨在准静态、动态载荷下不同加载位置的生物力学响应，以及小腿动态载荷下不同加载位置的生物力学响应，解决试验样本多样性造成的模型验证难题。当胫骨和腓骨皮质骨弹性模量分别取18.43和18.23 GPa、失效应变分别取1.2%和0.8%、小腿肉体体积模量取11.33 MPa时，所建小腿模型能够较好地同时满足多组试验中样本的生物力学响应，表明基于优化的多工况人体模型验证方法能够使有限元模型获得较好的生物逼真度。

小腿；中国人体；优化；有限元模型；验证

引言

交通安全问题是一个世界性难题,全球每年超过117万人在交通事故中丧生，受伤者更是达到1 000万人[1]。下肢是交通事故中最易受到损伤的部位之一[2]，包括膝关节损伤、长骨骨折等[3]。下肢损伤不仅给受害者造成巨大伤痛，也会给社会和家庭带来沉重负担。为更好地了解下肢损伤的机理，许多研究者采用尸体实验来研究下肢损伤，但由于实验成本高、样本难以获得且重复性差等原因，人体有限元模型获得了广泛应用。

在国外，下肢有限元模型发展较早。1993年，Bermond等就开发了包括股骨、胫骨和主要韧带的行人下肢模型，但几何外形不准确[4]。1998年，Wykowski等开发了乘员下肢有限元模型，只有骨骼并且将骨骼定义为刚体[5]。2005年，Untaroiu等基于LS-DYNA求解器，开发了行人下肢有限元模型，定义了肌腱、肌肉和皮肤，并进行了较详细的验证[6]。2013年，Untaroiu等基于先前的模型，更详细地提取骨骼几何外形，建立了乘员下肢有限元模型[7]。在国内，下肢有限元模型研究起步比较晚，2000年后一些学者根据国外模型进行了材料改进和验证[8-11]，并没有根据中国人体的几何外形建立中国人体下肢有限元模型。目前的下肢有限元模型大多都是根据欧美人体建立的，而中国人体在尺寸上与欧美人体存在较大差异，其生物力学响应与中国人体存在多大差异目前并不明确。

不同组织层次的全面验证是保证人体有限元模型生物逼真度的有效手段。但由于试验样本在几何尺寸、组织材料等方面的差异，造成不同样本的生物力学响应存在较大差异，这给模型验证带来了较大的挑战，尤其是要同时满足不同组织层次、不同载荷工况的多目标模型验证。

因此，为建立具有较高生物逼真度且良好适用性的中国50th人体有限元模型，本研究利用医学影像数据建立了中国50th人体小腿有限元模型，基于优化方法构建了模型验证方法，对不同组织层次、不同加载方向、不同加载位置等多种工况下的小腿模型进行了验证，使一个模型同时与多种试验数据吻合。

1 小腿有限元模型建立

1.1 几何模型

精确的几何模型是获得高质量有限元模型的基础。利用CT和MRI医学影像分别构建小腿长骨(胫骨和腓骨)和肉体几何，如图1所示。医学影像数据来源于一位骨骼正常的接近中国50th的男性血管疾病患者(身高173.1 cm，体重69.7 kg)。

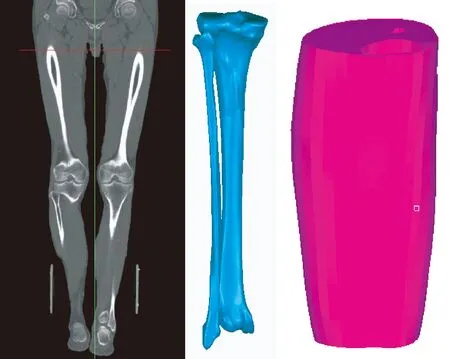
图1 小腿医学影像与胫骨、腓骨和肌肉的几何模型Fig.1 The medical imaging and geometry of the shank

1.2 有限元模型

综合使用ANSYSY ICEM CFD和Hypermesh对小腿模型进行网格划分。胫骨体皮质骨采用4层六面体网格模拟；胫骨两端皮质骨较薄，用壳单元模拟，松质骨采用体单元模拟。胫骨体与胫骨两端皮质骨过渡区域选用阶梯形状逐渐过渡，以减小应力集中，如图2所示。腓骨骨干皮质骨采用2层六面体单元模拟，两端皮质骨采用厚度为1.5 mm的壳单元模拟，骨干皮质骨与两端皮质骨的过渡同样采用阶梯形状。小腿的肉体采用实体单元模拟，用CONTACT_TIED_NODES_TO_ SURFACE将肌肉与胫骨、腓骨连接。皮肤采用壳单元模拟，使用共节点方式与肌肉连接。

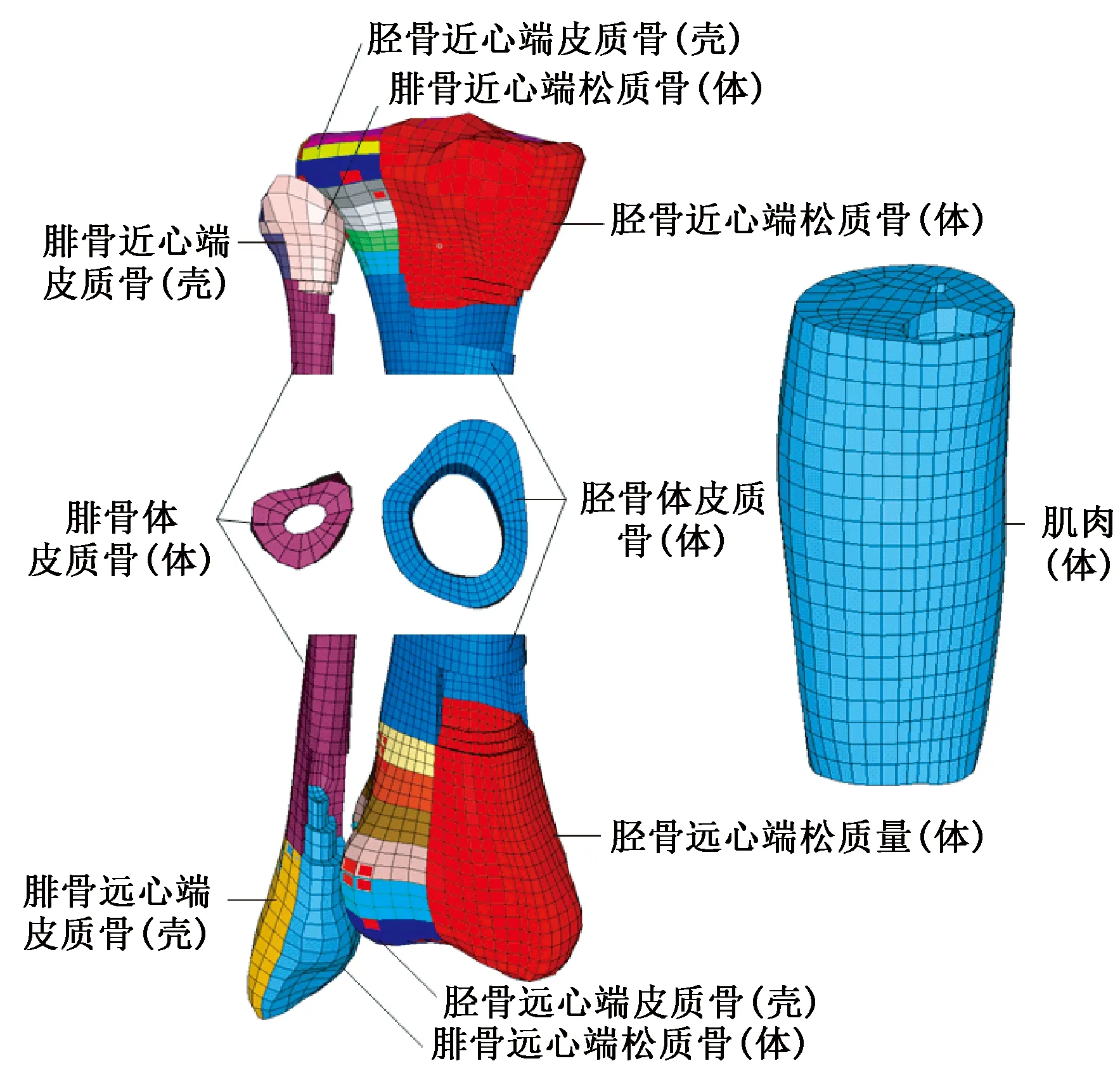
图2 小腿网格的划分Fig.2 The mesh division of legs

胫骨、腓骨模型雅克比小于0.60的单元比例不超过1%，最小值为0.42；翘曲度大于20°的单元比例不超过2%，最大值为120°；长宽比大于3.5的单元比例小于5%，最大值为5.2；最小单元尺寸4.69 mm，最大单元尺寸6.42 mm。

1.3 有限元模型尺寸缩放

由于本模型的人体尺寸(身高173.1 cm，体重69.7 kg)大于中国50百分位人体尺寸[12](身高 170.8 cm，体重65 kg)，需要将小腿模型缩放到中国50百分位人体小腿尺寸。在碰撞过程中，胫骨是决定小腿生物力学响应的主要部分，因此本研究依据胫骨尺寸对小腿模型进行缩放。

轴向缩放系数主要依据中国50百分位人体与本样本胫骨长的比例，横向缩放系数主要依据中国50百分位人体与本样本股骨上内关节面矢径和上外关节面矢径比例的平均值，纵向缩放系数主要依据中国50百分位人体与本样本的上段宽和下段宽比例的平均值[12]。最终确定胫骨的轴向缩放系数为0.965，横向缩放系数为0.969，纵向缩放系数为0.964，如表1所示。将胫骨模型按照3个方向缩放系数平均值缩放至中国50百分位男性胫骨的尺寸，并依据此比例对小腿腓骨、肉体和皮肤模型进行缩放，最终获得中国50百分位男性小腿有限元模型。

1.4 小腿材料模型

胫骨、腓骨的皮质骨采用可分别定义拉、压应力-应变曲线的弹塑性材料，应力-应变曲线初始值如图3所示[13]。采用黏弹塑性材料模拟松质骨。皮肤采用弹性材料模拟，密度为1 000 kg/m3，弹性模量为1 MPa，泊松比为0.3，厚度为1 mm[14-15]。肉体使用黏弹性材料模拟，密度为1 000 kg/m3，体积模量为20 MPa，超弹性系数C1为1.2×10-4MPa，超弹性系数C2为2.5×10-4MPa，普罗尼算法系数S1为1.162，普罗尼算法系数S2为0.808，普罗尼算法系数T1为10.43 ms，普罗尼算法系数T2为84.1 ms[16]。采用失效应变作为失效准则来模拟损伤，在材料达到设定的失效应变后自动删除失效单元。根据相关文献设定模型优化前各参数取值，如表2所示[14, 17-24]。

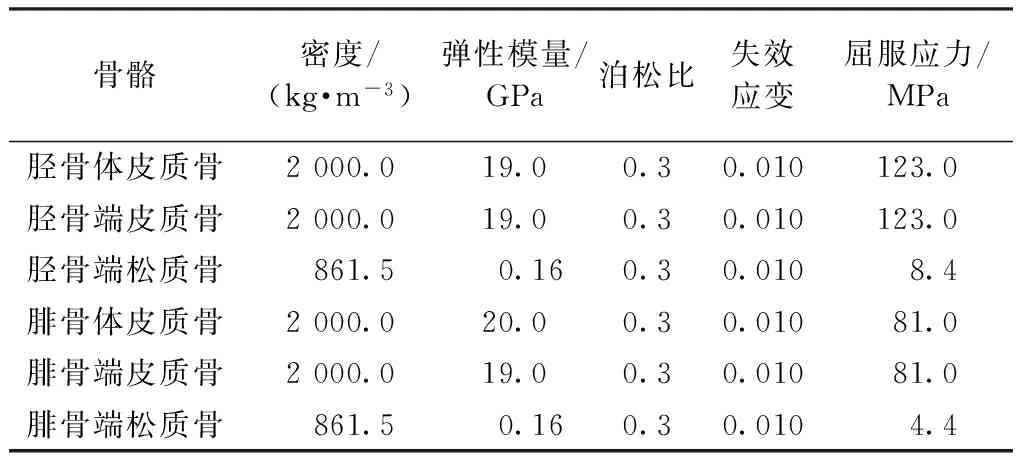
表2 小腿模型材料参数设置Tab.2 Material parameters of leg model

2 小腿有限元模型的优化验证

充分全面的验证是保证有限元模型适应性和逼真度的基础，本研究进行的模型验证包括准静态验证和动态验证，如表3所示。传统的验证方式采用试错法手动调节材料参数对模型进行验证，效率低且准确度有限。本研究采用优化方法自动获得最佳材料参数值，能同时保证模型的生物力学响应与多个试验结果吻合。

图4 小腿模型验证流程Fig.4 Flow chart of the shank model validation

先对胫骨近心端、中部、远心端3个加载位置的动态仿真进行胫骨体皮质骨的弹性模量和拉、压应力-应变曲线优化(此时未定义失效应变)，将得到的最佳材料参数更新到胫骨模型，然后对胫骨近心端、中部、远心端3个加载位置的动态仿真进行胫骨失效应变优化。同样,对腓骨进行类似的优化验证。接着将得到的最佳材料参数更新到小腿模型，对小腿近心端、中部、远心端3个加载位置的动态仿真进行肉体材料的体积模量优化。最终获取一组最佳材料参数，再对胫骨和腓骨的准静态试验进行校核。优化流程如图4所示，设计变量的取值范围如表4所示[7, 14, 19, 30-32]。

表3 小腿有限元模型验证Tab.3 Finite element model validation of the shank

注：A-P为载荷由前向后方向，L-M为载荷由外侧向内侧。

Note：A-P: loading direction from anterior to posterior；L-M: loading direction from lateral to medial.

表4 设计变量的取值范围Tab.4 The range of design variables

在胫骨和腓骨体皮质骨的弹性模量和拉、压应力-应变曲线优化中,设计变量分别弹性模量和拉、压应力-应变曲线横(应变)、纵(应力)坐标的缩放系数。在肌肉材料参数优化中，设计变量为体积模量。目标函数为仿真与实验的力-位移曲线的均方差f(X)的最小值[33]，即

(1)

式中：X为设计变量，k=1,2, …，K，K为实验曲线的条数；m=1,2, …，Pk，Pk为第k条曲线中计算点的个数；Wm为权重系数，本研究中各工况权重为1；fm(X)为响应面近似模型的计算值；Gm为实验测试点的值。

在胫骨和腓骨体皮质骨的失效应变优化中，设计变量为失效应变。目标函数为各工况仿真与实验的力-位移曲线的力极大值点对应的位移之差绝对值f(X)的最小值，即

(2)

式中：n=1,2,…，N，N为工况的个数；Xn为第n个工况中实验的力-位移曲线的位移最大值；Xsn为第n个工况中仿真的力-位移曲线的力极大值对应的位移。

在优化中，如果某个工况下的目标实验曲线有多个，则采用这些实验曲线的平均曲线作为该工况优化的目标曲线。平均曲线的计算方法参照Lessley等的计算(2004)[34]。

2.1 生物力学实验数据缩放

胫骨和腓骨动态仿真采用Takahashi等实验(2003)中胫骨长度为467 mm的数据[35]，小腿动态仿真采用Kerrigan(2008)缩放至美国50百分位人体的数据[36]。为了准确验证中国50百分位人体的有限元模型，还需将实验数据缩放到与中国50百分位人体几何相对应的数值，以消除尺寸差异对生物力学响应的影响。

Kerrigan(2008)为准确获得美国50百分位人体小腿的损伤耐受限度和弯曲响应，采用胫骨长度缩放系数λL计算位移缩放系数λD和力缩放系数λF，然后对实验数据进行缩放[2]，具体计算如下：

式中，L50th为美国50百分位人体的胫骨长度，L样本为试验样本的胫骨长度。

实验曲线中的位移、力、弯矩乘以相应的缩放系数，即可得到与美国50百分位相对应的曲线。按照上述实验数据缩放方法，只需将美国50百分位人体的胫骨长度缩放至中国50百分位人体的胫骨长度。

由于胫骨准静态试验所用胫骨长度尺寸不能确定，本研究只对胫骨、腓骨和小腿动态仿真的实验数据进行缩放。文献中胫骨、腓骨和小腿动态实验数据已经过缩放，所以本研究在胫骨、腓骨样本的近心端1/3处、中间、远心端1/3处的缩放系数相同，小腿样本的近心端1/3处、中间、远心端1/3处的缩放系数相同，如表5所示。实验样本的位移、力乘以相应缩放系数即可得到与中国50百分位人体尺寸相对应的缩放实验曲线。

表5 实验样本的缩放系数和胫骨长度

Tab.5 The scaling coefficients of the experimental samples and the length of the tibia

缩放参数胫骨L样本小腿L样本Prox.Mid.Dist.Prox.Mid.Dist.中国50thL50th胫骨长/mm391.00391.00391.00378.70378.70378.70354.02λL0.9050.9050.9050.9350.9350.935—λD0.9050.9050.9050.9350.9350.935—λF0.8190.8190.8190.8740.8740.874—

2.2 胫骨、腓骨和小腿模型动态模型

鉴于人体侧面遭受撞击的几率远大于其他方向[36]，本研究仅进行L-M方向的动态仿真。Kerrigan等(2003)和Kerrigan(2008)对胫骨、腓骨和小腿的近心端1/3处、中部、远心端1/3处进行了三点弯曲实验[28, 36]。在胫骨和腓骨的实验中，冲击块被一层厚25 mm的ConforTM 泡沫包裹，冲击速度为1.45 m/s，在小腿实验中，加载速度为1.5 m/s。Untaroiu等(2005)[2]和Takahashi等(2003)[16]使用其数据开展了模型验证。本研究参照上述实验和仿真建立胫骨、腓骨和小腿的动态三点弯曲验证模型，分别如图5～7所示。金属方盒、弧形板、支撑平板和冲击块均定义为刚体，泡沫定义为柔性体(Material #57)。长骨与金属盒的连接定义为刚性连接(*CONSTRAINED_EXTRA_NODES _SET)[2,16]。

图5 胫骨动态三点弯曲仿真模型Fig.5 Simulation of tibia dynamic 3-point bending test

图7 小腿动态三点弯曲仿真模型Fig.7 Simulation of shank dynamic 3-point bending test

图6 腓骨动态三点弯曲仿真模型
Fig.6 Simulation of fibula dynamic 3-point bending test

2.3 胫骨和腓骨模型准静态仿真模型

依据Yamada、Asang、Ehler相关文献[25-27]建立仿真模型。用直径为25 mm的刚性圆筒冲击器，以0.01 m/s的速度对长骨中部进行加载。根据载荷加载方向的不同，胫骨和腓骨准静态三点弯曲仿真分为A-P和L-M两个方向的验证。仿真设置如图8、9所示。

图8 胫骨准静态三点弯曲仿真模型。(a) A-P；(b) L-MFig.8 Quasi-static 3-point bending simulation of tibia. (a) A-P; (b) L-M

图9 胫骨准静态三点弯曲仿真模型。(a) A-P；(b) L-MFig.9 Quasi-static 3-point bending simulation of fibula. (a) A-P; (b) L-M

3 模型仿真结果

3.1 优化结果

图10列出了典型的设计变量在优化过程中的收敛历程。随着迭代次数的增加，各设计变量兴趣域空间逐渐缩小，各参数取值逐渐稳定。最终胫骨体皮质骨弹性模量为18.43 GPa，拉、压应力-应变曲线横、纵坐标的缩放系数分别为2.560和0.684，失效应变为1.2%；腓骨体皮质骨弹性模量为18.23 GPa，拉、压应力-应变曲线横、纵坐标的缩放系数分别为2.888和0.725，失效应变为0.8%；小腿肉体积模量为11.33 MPa。

图10 材料参数收敛过程。(a)胫骨弹性模量；(b) 胫骨应力-应变曲线横坐标(应变)缩放系数；(c) 胫骨应力-应变曲线纵坐标(应力)缩放系数；(d) 小腿体积模量Fig.10 Convergence process of material parameters. (a) Elastic modulus of the tibia; (b) Abscissa scaling factor of the tibial stress-strain curve; (c) Ordinate scaling factor of the tibial stress strain curve; (d) Bulk modulus of the shank

3.2 动态仿真优化结果

胫骨、腓骨和小腿材料参数优化后，仿真结果与缩放后试验曲线的对比分别如图11～13所示。

图11 胫骨动态三点弯曲优化验证结果。(a)近心端1/3处；(b)中部；(c)远心端1/3处Fig.11 Dynamic 3-point bending validation results for tibia against test results with optimization method. (a) Proximal 1/3; (b) Middle-shaft; (c) Distal 1/3

图12 腓骨动态三点弯曲优化验证结果。(a)近心端1/3处；(b)中部；(c)远心端1/3处Fig.12 Dynamic 3-point bending validation results for fibula against test results with optimization method. (a) Proximal 1/3; (b) Middle-shaft; (c) Distal 1/3

图13 小腿动态优化验证与缩放后的试验曲线。(a)近心端1/3处；(b)中部；(c)远心端1/3处Fig.13 Dynamic 3-point bending validation results for shank against test results with optimization method. (a) Proximal 1/3; (b) Middle-shaft; (c) Distal 1/3

由图11～图13可知，胫骨动态三点弯曲仿真的近心端1/3处和远心端1/3处力-位移曲线与目标曲线吻合程度较好；胫骨中部三点弯曲仿真的力-位移曲线在上半段与目标曲线拟合较好，虽然在下半段存在一些偏差，但曲线的走势基本一致。腓骨近心端、中部、远心端3处加载位置的动态仿真都与目标曲线吻合良好。小腿近心端和中部加载位置的动态仿真与目标曲线吻合较好，但在远心端1/3加载位置的仿真结果不够理想。

3.3 准静态仿真结果

使用优化后的材料参数进行胫骨和腓骨A-P、L-M两个加载方向的准静态三点弯曲仿真。由于实验涉及的胫骨长度无法确定，在准静态仿真时未对实验曲线进行缩放。胫骨和腓骨的验证结果分别如图14、15所示。仿真结果在实验曲线范围内，并与实验曲线保持了较好的一致性。模型发生损伤时的变形量和碰撞力也与实验曲线吻合较好。

图14 胫骨准静态三点弯曲验证结果。(a) A-P；(b) L-MFig.14 Quasi-static 3-point bending validation results for tibia against test results with optimization method

图15 腓骨准静态三点弯曲验证结果。(a) A-P；(b) L-MFig.15 Quasi-static 3-point bending validation results for fibula against test results with optimization method. (a) A-P; (b) L-M

4 讨论

本研究采用优化方法对所建立的中国50th男性人体小腿有限元模型进行了全面的验证，股骨和胫骨的弹性模量、应力-应变曲线缩放系数、失效应变和小腿肉的体积模量等设计变量均能够有效收敛于最优值。胫骨和腓骨皮质骨的弹性模量分别为18.43和18.23 GPa，这与多个文献给出的14.3～21.1GPa[19, 37-38]的范围一致。胫骨和腓骨皮质骨的失效应变分别为1.2%和0.8%，这与文献[19]基本一致。小腿肉的体积模量为11.33 MPa，也在文献给出的1.33～29.2 MPa[16,39]的范围内。

腓骨近心端、中部和远心端3处不同加载位置的动态仿真都与试验曲线吻合良好，A-P、L-M两个加载方向的准静态仿真也与试验曲线吻合较好。胫骨近心端和远心端加载位置的动态仿真以及A-P、L-M两个加载方向的准静态仿真均与试验结果吻合良好，但中部加载位置的动态仿真与试验结果有一定差异。小腿中部加载的动态仿真与试验结果吻合较好，但近心端和远心端加载位置的动态仿真与试验结果有一定差异。上述验证所涉及的生物力学试验对应的试样样本较多，样本年龄分布较广，个体差异带来较大的生物力学响应的差异。因此，用一套材料参数同时满足基于不同样本的多组试验曲线存在较大的现实难度。通过多工况同时优化并设置相同的权重，能够最大限度地保证仿真结果的总体拟合效果。

由于缺少中国人体的生物力学试验数据，本研究开展验证所用的试验数据均来源于欧美人体。但中国人体与欧美人体在解剖学结构方面存在一定的差异，而基于缩放方法的试验数据缩放，能够在一定程度上减小解剖学结构差异对模型验证的影响。不管中国人体还是欧美人体均属人类，两者在力学特性及材料参数方面虽存在差异，但可能并不大。但是，将来仍需要针对中国人体开展相应的生物力学试验，以揭示与欧美人体在力学特性方面的差异，并为中国人体数学模型的研究提供基础性数据支持。

5 结论

本研究通过CT和MRI医学影像数据建立了小腿骨骼和肉体几何模型，并根据人体统计学数据将小腿模型缩放到中国50百分位人体尺寸。使用优化方法，对胫骨、腓骨和小腿不同加载位置的仿真进行优化，获得了理想的材料参数，并能够满足准静态下胫骨和腓骨不同加载方向的生物力学逼真度。结果表明，所建立的中国人体50百分位小腿模型具有较高的生物逼真度，基于优化和缩放方法的人体有限元模型验证方法能够有效解决试验样本几何、材料多样性带来的多工况试验数据拟合问题，保证模型具有较好的生物逼真度和较广泛的适用性。

[1] Zhang Guanjun, Cao Libo, Hu Jingwen, et al. A field data analysis of risk factors affecting the injury risks in vehicle-to-pedestrian crashes [J]. Ann Adv Automot Med, 2008, 52: 199-214.

[2] Kim YS, Choi HH, Cho YN, et al. Numerical investigations of interactions between the knee-thigh-hip complex with vehicle interior structures [J]. Stapp Car Crash J, 2005, 49: 85-115.

[3] Yang Jikuang. Injury biomechanics in car-pedestrian collisions: development, validation and application of human-body mathematical models [D]. Gothenburg: Chalmers University of Technology, 1997.

[4] Bermond F, Ramet M, Bouquet R, et al. A finite element model of the pedestrian knee joint in lateral impact [C] // Proceedings of the International Research Council on the Biomechanics of Injury Conference. Eindhoven: INRETS-Bron, 1993: 117-129.

[5] Wykowski E, Sinnhuber R, Appel H. Finite element model of human lower extremities in a frontal impact [C]//Proceedings of the International Research Council on the Biomechanics of Injury Conference. Goteborg: IRCOBI Secretariat, 1998: 101-116.

[6] Untaroiu CD. Development and validation of a finite element model of human lower limb: including detailed geometry, physical material properties, and component validations for pedestrian injuries [D]. Charlottesville: University of Virginia, 2005.

[7] Untaroiu CD, Yue N, Shin J. A finite element model of the lower limb for simulating automotive impacts [J]. Annals of Biomedical Engineering, 2013, 41(3): 513-526.

[8] 杨济匡, 方海峰. 人体下肢有限元动力学分析模型的建立和验证 [J]. 湖南大学学报(自然科学版), 2005, 32(5): 31-36.

[9] 张冠军. 行人下肢的碰撞损伤特性及相关参数研究 [D].长沙: 湖南大学, 2009.

[10] 李正东, 刘宁国, 黄平, 等. 下肢有限元模型的建立及损伤机制重建 [J]. 中国司法鉴定, 2012(6): 37-42.

[11] 蒋小晴, 杨济匡, 王丙雨, 等. 乘员股骨在轴向压力-弯矩下的损伤生物力学机理研究 [J]. 力学学报, 2013, 46(3): 465-474.

[12] 刘俊先, 张兴和. 中国正常人体测量值 [M]. 北京: 中国医药科技出版社, 1994: 62-63.

[13] Novitskaya E, Chen PY, Hamed E, et al. Recent advances on the measurement and calculation of the elastic moduli of cortical and trabecular bone: a review [J]. Theoretical and Applied Mechanics, 2011, 38(3): 209-297.

[14] Beillas P, Begeman PC, Yang KH, et al. Lower limb: advanced FE model and new experimental data [J]. Stapp Car Crash J, 2001, 45: 469-494.

[15] Karimi A, Navidbakhsh M. Material properties in unconfined compression of gelatin hydrogel for skin tissue engineering applications [J]. Biomedical Engineering/ Biomedizinische Technik, 2014, 59(6): 479-486.

[16] Snedeker JG, Muser MH, Walz FH. Assessment of pelvis and upper leg injury risk in car-pedestrian collisions: comparison of accident statistics, impactor tests and a human body finite element model [J]. Stapp Car Crash J, 2003, 47: 437-458.

[17] Iwamoto M, Tamura A, Furusu K, et al. Development of a finite element model of the human lower extremity for analyses of automotive crash injuries [C] //SAE 2000 World Congress. Detroit: SAE International, 2000: 2000-01-0621.

[18] Schuster PJ, Chou CC, Prasad P, et al. Development and validation of a pedestrian lower limb non-linear 3-d finite element model [J]. Stapp Car Crash J, 2000, 44: 315-334.

[19] Takahashi Y, Kikuchi Y, Konosu A, et al. Development and validation of the finite element model for the human lower limb of pedestrians [J]. Stapp Car Crash J, 2000, 44: 335-355.

[20] Chawls A, Mukherjee S, Mohan D, et al. Validation of lower extremity model in THUMS [C] //Proceedings of the International Research Council on the Biomechanics of Injury conference. Graz: IRCOBI Secretariat, 2004: 155-166.

[21] Arnoux PJ, Cesari D, Behr M, et al. Pedestrian lower limb injury criteria evaluation: a finite element approach [J]. Traffic Injury Prevention, 2005, 6(3): 288-297.

[22] Untaroiu C, Darvish K, Crandall J, et al. A finite element model of the lower limb for simulating pedestrian impacts [J]. Stapp Car Crash J, 2005, 49: 157-181.

[23] Silvestri C, Ray M. Development of a finite element model of the knee-thigh-hip of a 50th percentile male including ligaments and muscles [J]. International Journal of Crashworthiness, 2009, 14(2): 215-229.

[24] Neale M, Thomas R, Bateman H, et al. A finite element modelling investigation of lower leg injuries [C] //Proceedings of the 20th International Technical Conference on the Enhanced Safety of Vehicles (ESV). Lyon: NHTSA, 2007: 07-0077.

[25] Yamada H. Strength of biological materials [M]. Baltimore: The Williams & Wilkins Company, 1970: 49-73.

[26] Ehler E, Lösche H. Die menschliche tibia unter biegebelastung [J]. Beitr. Orthop, 1970, 17(5): 291-304.

[27] Asang E. Experimental biomechanics of the human leg: a basis for interpreting typical skiing injury mechanisms [J]. The Orthopedic Clinics of North America, 1976, 7(1): 63-73.

[28] Kerrigan J, Ivansson B, Bose D, et al. Rate-sensitive constitutive and failure properties of human collateral knee ligaments [C]//Proceedings of the International Research Council on the Biomechanics of Injury conference. Lisbon: IRCOBI Secretariat, 2003: 177-190.

[29] Begeman P, Paravasthu N. Static and dynamic compression loading of the lower leg [C]//Proceedings of the Seventh Injury Prevention Through Biomechanics Symposium. Detroit: Wayne State University, 1997.

[30] Burstein AH, Reilly DT, Martens M. Aging of bone tissue: mechanical properties [J]. J Bone Joint Surg Am, 1976, 58(1): 82-86.

[31] Martens M, van Audekercke R, Delport P, et al. The mechanical characteristics of cancellous bone at the upper femoral region [J]. Journal of Biomechanics, 1983, 16(12): 971-983.

[32] Galbusera F, Freutel M, Dürselen L, et al. Material models and properties in the finite element analysis of knee ligaments: a literature review[J]. Frontiers in Bioengineering and Biotechnology, 2014, 2: 1-11.

[33] 官凤娇. 冲击载荷下的生物组织材料参数反求及损伤研究 [D]. 长沙: 湖南大学, 2011.

[34] Lessley D, Crandall J, Shaw G, et al. A normalization technique for developing corridors from individual subject responses [C] //SAE 2000 World Congress. Detroit: SAE International, 2004: 2004-01-0288.

[35] Takahashi Y, Kikuchi Y, Mori F, et al. Advanced finite element lower limb model for pedestrians [C] //Proceedings of the 18th International Technical Conference on the Enhanced Safety of Vehicles (ESV). Lyon: NHTSA, 2003: No 218.

[36] Kerrigan JR. A computationally efficient mathematical model of the pedestrian lower extremity [D]. Charlottesville: University of Virginia, 2008.

[37] Rho JY, Ashman RB, Turner CH. Young's modulus of trabecular and cortical bone material: ultrasonic and microtensile measurements [J]. J Biomech, 1993, 26(2): 111-119.

[38] Snyder SM, Schneider E. Estimation of mechanical properties of cortical bone by computed tomography [J]. J Orthop Res, 1991, 9(3): 422-431.

[39] Ruan J, El-Jawahri R, Chai L, et al. Prediction and analysis of human thoracic impact response and injuries in cadaver impacts using a full human body finite element model [J]. Stapp Car Crash J, 2003, 47: 299-321.

Study on FE Modeling Method of the 50th Percentile Chinese Shank with Optimization Methods under Multi-Loading Condition

Zhang Guanjun1Wang Longliang1Deng Xiaopeng1Du Xianping1Guan Fengjiao2*

1(StateKeyLaboratoryofAdvancedDesignandManufacturingforVehicleBody,HunanUniversity,Changsha410082，China)2(CollegeofMechatronicEngineeringandAutomation,NationalUniversityofDefenseTechnology,Changsha410073,China)

The lower extremity of the human body is one of the most vulnerable parts in traffic accidents, and the finite element (FE) model of the lower limb has become an important tool to study mechanisms and protective methods of lower limb injuries. In order to ensure the fidelity of the model, it is necessary to carry out a comprehensive validation under multi-loading conditions. The biomechanical test data are different in the mechanical response due to the sample size and material diversity, so it is difficult to use one model to meet the multiple test data. The differences in geometric dimensions between Chinese and occidental human body would result in differences of biomechanical response, so it is necessary to develop the FE model of Chinese human body. In this paper, Geometry model based on the CT and MRI data was scaled to the 50 percentile male according to scaling factor derived from key dimensions of the tibia. The scaling method was also used to scale biomechanical test data to the biomechanical response data corresponding to the size of the leg. The elastic modulus, stress-strain curve, failure strain of the tibia and fibula and physical bulk modulus of the muscle were selected as design variables, the optimization method was used to fit tibia, fibula and calf biomechanical responses under different load positions in the quasi-static and dynamic loading conditions, which solved the problem with diversity caused by the test sample. When the elastic modulus of tibia and fibula were 18.43 and 18.23GPa, respectively, the failure strains were 1.156% and 0.8%, respectively, and physical bulk modulus of the calf was 11.33MPa, the calf model could fit the biomechanical responses well in many groups of tests. The FE model verification methods based on the optimization of multi-loading conditionsmade the FE model acquire better biofidelity effectively.

shank; Chinese human body; optimization; finite element model; validation

10.3969/j.issn.0258-8021. 2017. 02.010

2016-06-29， 录用日期:2016-09-07

国家自然科学基金(11402296)；中央高校基本科研业务费(531107040162)；湖南大学汽车车身先进设计制造国家重点实验室自主研究课题(51475002)

R318

A

0258-8021(2017) 02-0195-010

*通信作者(Corresponding author)，E-mail: gfj0921@163.com