基于隐马尔可夫模型的老年人跌倒行为检测方法研究

曹荟强 林仲志 吴水才*

1(北京工业大学生命科学与生物工程学院，北京 100124)2(长庚大学资讯工程系，台湾 桃园 33302)

基于隐马尔可夫模型的老年人跌倒行为检测方法研究

曹荟强1林仲志2吴水才1*

1(北京工业大学生命科学与生物工程学院，北京 100124)2(长庚大学资讯工程系，台湾 桃园 33302)

随着社会老龄化程度的加剧，老年人的安全健康监护需求日益增加。跌倒行为在老年人日常生活中比较常见，它会给老年人带来严重的身体及心理伤害。因此，跌倒检测对于保护老年人的健康及安全具有重要意义。针对跌倒的运动过程，分析人体加速度变化特征，提出基于隐马尔可夫模型(HMM)的跌倒检测方法。将人体跌倒的加速度信号提取为加速度观测序列，并以此为训练样本训练隐马尔可夫模型，建立跌倒过程的概率模型进行跌倒检测。在验证实验中，采集10名志愿者共300例样本，采用5折交叉检验方法，对模型的有效性进行验证。验证结果表明，该方法检测跌倒的准确率为98.2%，灵敏度为91.3%，特异性为99.6%，具有良好的检测效果，可实现对跌倒行为的准确检测。

跌倒检测；加速度时序；隐马尔可夫模型

引言

我国老年人口基数大、增速快，高龄化趋势明显。截至2014年底，我国60岁及以上的老年人口已达2.12亿人，占总人口的15.5%。高龄人口的增长致使社会老龄化的程度加剧，老年人的健康照护成为严峻的社会问题。跌倒行为是人体姿态动作异常的情况之一，老年人在日常生活中发生跌倒的几率较高。研究表明，65岁以上的老年人口中，约1/3的人群均发生过跌倒，并且伴随年龄增长，发生跌倒的几率也会增加[1-2]。跌倒可致老年人伤残甚至死亡，给家庭和个人都带来负面影响。因此，运用现代技术检测跌倒行为的发生对于老年人的健康照护至关重要，跌倒发生后的及时救助对降低老年人的伤残率和死亡率具有重要意义。

在目前跌倒检测的研究中，信号、数据的获取来源主要有两种途径：基于视觉图像设备[3-6]和基于穿戴式设备[7-10]。基于视觉图像设备的方法多使用图像采集设备(如摄像头)获取图像信息，同时对图像进行分析处理，进而判断人的姿态或者运动状态。这种方法应用广泛，但会受到采集图像的清晰程度以及安装成本的影响，并且监护的覆盖范围有限。基于穿戴式设备的方法多使用运动传感器对人体运动进行感测，常用的运动传感器有加速度传感器、角速度计以及磁力计等，其采集人有效部位的运动数据，以分析运动信号的方式解释人的运动状态，并对运动异常情况(如跌倒行为)进行判别。穿戴式设备简单易用、成本低廉，并且运动传感器的精度提高使得其对运动状态、运动行为的反映更为真实准确，因此基于穿戴式设备进行跌倒检测成为兼具准确与实用的方法。

在跌倒检测的算法设计方面，使用机器学习或数学统计这两种方式来分析数据、判断跌倒较为常见。机器学习方法有支持向量机(support vector machine, SVM)[7]、BP神经网络[11]和极限学习机[12]等；数学统计是归纳出跌倒过程信号或数据的变化特征，设定阈值来判断跌倒[13-16]。这两种方式存在一定的局限性，机器学习的分类特征不容易确定，并且学习训练的时间成本高，不适用于实时检测；而设定阈值检测跌倒，判断标准的维度单一，忽略了跌倒行为的运动特征；同时，阈值受实验个体影响较大，不能描述跌倒过程的完整信息，因此“阈值法”误报率较高。

由于这些局限性的存在，建立数学模型来描述跌倒行为进而判断跌倒的研究越来越多。隐马尔可夫模型(hidden Markov model， HMM)是针对随机过程特点建立的概率模型，其可描述识别时序过程，在语音识别、行为识别等多个领域应用广泛[17-22]。建立跌倒过程模型来检测跌倒，优点是模型由跌倒过程的数据训练建立，完整地描述跌倒过程的数据特点；另外，HMM的学习训练过程简单，识别跌倒所要求的计算能力低，与机器学习相比具有明显的优势，适用于实时监测的情况。因此，本研究提出了一种基于隐马尔可夫模型的跌倒行为检测方法，定义跌倒为一种运动过程，使用单个三轴加速度传感器来采集人体跌倒过程的加速度信号，分析信号的变化特征，提取跌倒过程的观测序列，使用跌倒过程观测序列进行模型训练，建立描述跌倒过程的HMM，并通过实验来验证方法的可行性。

1 材料和方法

1.1 方法原理

1.1.1 跌倒行为的加速度特点

跌倒行为是人身体突然失去平衡、意外倒地的现象。在跌倒过程中，人的受力情况会使身体运动的加速度发生变化。跌倒过程依次包括4个阶段：跌倒前阶段、失衡阶段、跌倒阶段和跌倒后阶段。其中，跌倒前阶段为失衡开始前的阶段；失衡阶段开始后，身体在短时间内处于失重状态，加速度向0g(g为重力加速度)趋近；跌倒阶段，加速度变化反复，数值变化幅度大；跌倒后阶段，加速度曲线趋于平稳。人体跌倒行为加速度曲线如图1所示。

图1 跌倒过程加速度变化曲线Fig.1 Carve characteristic for fall process

在跌倒过程加速度曲线中，加速度最大值点为跌倒点[12]，将跌倒点及之前0.5 s的运动过程定义为跌倒过程。通过分析跌倒过程的加速度曲线可发现，失衡阶段和跌倒点是跌倒过程中最显著的特点，其描述了跌倒过程中人由站立到倒地的变化，体现了跌倒过程中人运动状态的改变；此外，由于跌倒具有偶然和突发的动作属性，与日常活动已形成的固有行为模式不同，受个体差异影响小，不同个体在跌倒时产生的加速度变化具有相似且一致的变化特征，所以失衡阶段和跌倒点是与个体特征关联较小的可测量量，具有普适性[20，23]。因此，失衡阶段的加速度变化以及跌倒点可作为跌倒检测的依据。

1.1.2 HMM的基本概念

HMM是统计模型，用来描述一个具有隐含未知参数的马尔可夫过程。HMM由双重随机过程组成，一个是隐含状态转移序列，其中隐含的状态不能直接观察到；另一个是与隐含状态相关的观测序列，每一个观测序列是由具有相应概率密度分布的状态序列产生[24]。

1.1.2.1 基本要素

1)隐含状态数M，隐含状态集合为S={s1,s2,…,sM}。

2)观测序列数N，观测序列集合为V={v1,v2,…,vN}。

3)状态转移的概率分布A，表示为A={aij}。其中，A表示时刻t从状态si转移到时刻t+1状态sj的转移概率；aij=P{qt+1=sj|qt=si}，1≤i，j≤M，qt为t时刻的状态。

4)观测序列的概率分布B，可表示为B={bj(k)}，bj(k)=P{vt|qt=sj}，1≤j≤M，1≤k≤N，表示状态sj输出各观测变量的概率。

5)初始状态概率分布π，表示为π={πi，1≤i≤M}，πi=P{q1=si}。

1.1.2.2 基本问题[24]

1)评估问题。在给定模型λ条件下，计算λ产生观测序列O=O1,O2, …,OL的概率P(O|λ)，P描述了观测序列与模型间的匹配程度。

2)解码问题。给定模型λ和观测序列O=O1,O2, …,OL，求解对应最大概率的状态序列Q。

3)学习问题。通过观测序列O=O1,O2, …,OL，训练相应的HMM，求取模型λ的初始参数的最优解，使P(O|λ)达到最大。

1.2 跌倒检测算法

本研究使用台湾长庚大学生物资讯实验室健康智慧衣来采集人体运动加速度数据，将三轴加速度传感器安置于人体胸前，采样频率设定为100 Hz。假设ax、ay和az分别表示三轴传感器在x轴、y轴和z轴上的原始数据，则加速度传感器的采样数据可计算为

(1)

式中，asvm作为原始数据参与到HMM训练和跌倒行为识别中。

1.2.1 加速度观测序列提取

人在运动过程中，由于重力作用、身体活动和外力影响，使得自身加速度实时变化，分析加速度传感器所得的采样数据，可辨别身体运动的不同状态。为了分析时间T内的运动情况，对T内的加速度采样数据进行处理，以提取T内加速度观测序列，表征此时人体运动的状态变化。设定T=0.5 s，与跌倒过程的时间相同。观测序列的提取过程如下：

1)时间窗截取0.5 s的加速度采样数据，得到数据集{ai}(i=50)。数据集{ai}平均分割为10个数据单元，求取每个数据单元中采样数据的平均值o，按时间顺序排列得到时序{oi}(i=10)。

2)时序{o}特征值化。由于运动过程中加速度采样数据的变化范围大，为了区别运动状态的不同等级，将加速度采样数据的变化值域进行区段划分，并定义每一区段的特征值。时序{o}特征值化，得观测序列{Oi}(i=10)，转换公式如下：

(2)

式中，oi是转换前的加速度时序，Oi是转换后的观测变量。

1.2.2 跌倒过程HMM训练

HMM的训练过程就是解决HMM的学习问题，采用经典的Baum-Welch算法进行训练。Baum-Welch算法的核心在于通过递归迭代方式更新状态概率权重，使模型参数更好地解释训练样本序列[23]。训练跌倒过程HMM首先要获取跌倒过程的加速度观测序列，方法同本文第2.1节所述，其时间窗截取的数据集为跌倒过程的采样数据。

1.2.2.1 参数测定

要设定跌倒过程HMM的初始参数λ=(M,N,π,A,B)，具体参数设定如下：

1)隐含状态数M=3，隐含状态分别为平衡，失重、跌倒，隐含状态集合S={s1,s2,s3}。

2)观测序列数N=5，与观测序列的特征值个数相同，特征值与观测变量相对应，观测变量集合V={vi,vi=i}(i=1,2,…,5)。

3)状态转移的概率分布A如下：

s1s2s3

A=s1

s2

(3)

4)观测序列的概率分布B如下：

v1v2v3v4v5

(4)

5)初始状态概率分布π如下：

(5)

1.2.2.2 训练步骤

跌倒初始模型λ设定后，采用Baum-Welch算法进行模型训练，步骤如下：

1)取跌倒过程观测序列{Oi}(i=10)及跌倒初始模型λ，计算前向变量αt(i)，其含义为λ在时刻t处于运动状态si，此时观测序列为{Oi}的概率，后向变量βt(i)，表示λ在时刻t处于运动状态si，并且输出t时刻之后的观测序列为{Oi}的概率。前向变量和后向变量的计算如下：

αt(i)=P(O1,O2,…，O10,qt=si|λ)

(6)

βt(i)=P(O1,O2,…，O10|qt=si,λ)

(7)

应用前向变量和后向变量，可得到模型λ产生观测序列{Oi}(i=10)的输出概率P(O|λ)，即解决了HMM的评估问题。该值的含义是观测序列与模型的匹配程度，其计算过程如下：

(8)

式中，L是观测序列的长度，本研究中取L=10。

2)结合前向变量和后向变量，计算在时刻t处于运动状态si、其时刻t+1处于运动状态sj的概率γt(i，j)，计算观测序列{Oi}(i=10)在时刻t处于运动状态为si的概率δt(i)，有

(9)

(10)

3)使用HMM模型的重估公式，对模型进行重估并暂存结果。取下一个跌倒过程观测序列，此时模型参数为暂存结果参数;重复以上所有步骤直至用尽所有训练数据集，最终得到最优的跌倒过程模型λFall。HMM模型的重估公式如下：

(11)

(12)

式中，k等于观测序列数N，本研究中k=5。

1.2.3 跌倒检测算法应用

基于HMM的跌倒算法可实时检测跌倒行为是否发生，所处理的资料为实时采集的加速度采样数据asvm，跌倒检测算法的应用流程如图2所示。

图2 跌倒检测算法应用流程Fig.2 Diagram of fall detection method

在加速度采样数据中，设置0.5 s的滑动数据窗，窗的移动步长为0.01 s。滑动数据窗截取到的数据，按照本文第2.1节小结的方法进行加速度观测序列提取；将观测序列输入到跌倒过程模型λfall中，按照式(6)～(8)计算输出概率P(O|λfall)，即该观测序列与跌倒过程模型相匹配的概率。其中，输出概率与Pth进行比较，当大于Pth时，判断该观测序列为跌倒过程；否则，就不是跌倒过程。通过统计，跌倒过程观测序列得到的输出概率最小值为51.4%，故设定Pth=51.4%。

1.3 实验验证

1.3.1 数据采集

为获取跌倒过程和日常活动行为的加速度数据，设计实验进行数据采集。实验者为10名男性学生，年龄在22～24岁，身高165～178 cm，体重51～76 kg。出于安全考虑，未请老年人参与。实验者模拟老年人的日常活动行为，包括行走、慢跑、坐下起立以及3种不同方向的跌倒行为共6种活动动作，每种行为重复5次，除步行和慢跑两种活动的实验时长为20 s，另4种活动在5 s内完成。实验者活动行为描述见表1。

表1 实验者活动行为描述Tab.1 The description of movements process

1.3.2 跌倒模型验证

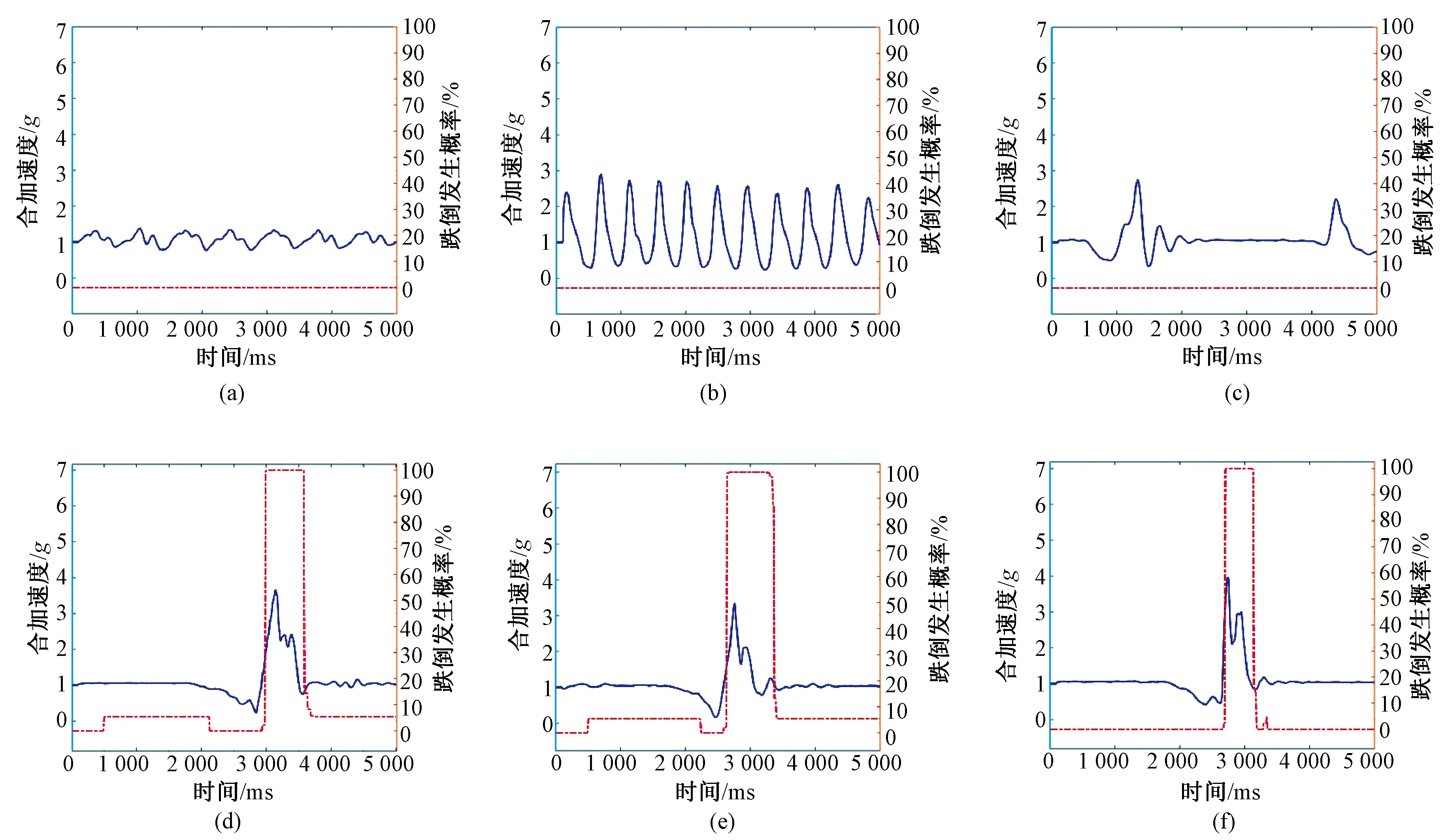
图3 6种活动行为跌倒检测结果。(a)步行；(b)慢跑；(c)坐下起立；(d)前向跌倒；(e)后向跌倒；(f)侧向跌倒Fig.3 Detection results of 6 kinds of motion process. (a)Walk；(b)Run；(c)Sit - Up；(d)Fall forward；(e)Fall backward；(f)Fall aside

10名实验者加速度样本共300例，其中跌倒行为样本150例，日常活动样本150例。由于样本数量少，因此采用5折交叉检验来对模型的检测效果进行考察。将跌倒行为样本平均分为5组，每组的样本从跌倒行为样本中随机抽取，数量为30；轮流将其中4组跌倒数据用作模型训练，另一组跌倒数据与日常活动样本用于模型测试。

在实验中，使用准确率、灵敏度和特异性3项作为跌倒检测模型效果的评价指标，其定义分别为

(13)

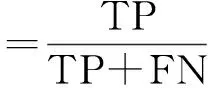
(14)

(15)

式中，TP为跌倒样本中被检测为跌倒的数量；TN为未跌倒样本中被检测为未跌倒的数量；FP为未跌倒样本中被检测为跌倒的数量；FN为跌倒样本中被检测为未跌倒的数量。

2 结果

图3为6种活动行为的加速度曲线，以及应用跌倒检测算法检验样本各时间点发生跌倒的概率曲线。

可以看出，图3(a)～(f)分别为步行、慢跑、坐下起立、前向跌倒、后向跌倒、侧向跌倒的加速度曲线，以及0.5 s滑动数据窗经由跌倒检测模型λfall计算得到的跌倒概率变化曲线。其中，(a)～(c)均是日常活动行为，任意时刻跌倒概率曲线在0附近波动；(d)～(f)均是跌倒行为， 滑动时间窗移动到跌倒发生处，模型计算所得概率升高，概率曲线呈现上升趋势，在特定区段跌倒概率为100%，此时检测到跌倒发生，与实际情况相符。在跌倒发生之后，身体已与地面接触，模型计算跌倒的概率降低至0附近。

考察算法的检测效果采用了5折交叉检验的方法，各测试集的验证结果见表2。

表2 基于HMM跌倒检测算法有效性结果Tab.2 The effectiveness of HMM fall detection method

在5组测试集对算法进行验证的结果中，方法的准确率均达到了95%，第2组测试集的准确率达到了98.9%，为5组测试集中的最高值；第1、4组的准确率最低，为97.8%。第1、2组测试中的灵敏度为93.3%，为5组中最高；最低值为90%。特异性的结果中有3组达到了100%，第1组结果最低，为98.7%。基于HMM的跌倒行为检测算法，准确率、灵敏度和特异性评估为测试集检验模型的各项结果的平均值，即准确率为98.2%、灵敏度为91.3%、特异性为99.6%。

3 讨论

现如今，随着我国老年人口的持续增长，社会老龄化程度加剧。对于老年人而言，身体条件日益下降，保持身体平衡的能力越来越差，跌倒十分容易发生。跌倒与其所造成的影响已是身体健康与生活独立的最大的威胁，轻则身体外伤，严重会导致死亡。因此，研究一种有效的跌倒检测方法尤为重要。跌倒检测方法不仅可以为老年人提供安全保护，而且保证了日常生活的健康独立；在医护环境下，跌倒检测使医护人员能立即获知病患跌倒，从而提供及时的医疗救助以及病情的快速评估，这对于提高医护质量同样意义重大。穿戴式设备结合加速度传感器可准确表达人的运动状态，用其进行跌倒检测具有简单易用的优势，相比图像处理实用性更高。相比机器学习进行分类或者设置阈值的跌倒检测算法设计，建立隐马尔可夫模型，用数学概率模型描述跌倒加速度过程，并用模型进行跌倒检测，不仅是一种新的探索，更在保证准确率、提高特异性上具有优势。

隐马尔可夫模型是描述时间序列过程的概率模型。跌倒的加速度数据被定义为跌倒前阶段、失衡阶段到跌倒阶段的转化过程，对加速度数据进行序列提取，得到加速度观测序列，并以此训练跌倒模型。通过计算给定观测序列与跌倒模型的匹配程度，以判断跌倒是否发生。实验结果表明，建立隐马尔可夫模型对跌倒行为的加速度数据进行分析是有效的。在移动时间窗处理所有数据点的过程中，只有时间窗中的加速度数据满足跌倒过程特点时，其与跌倒模型的匹配程度才会明显升高。图3(a)～(c)的3种活动行为均未发生跌倒，滑动时间窗在任何时刻提取出的加速度观测序列都不满足跌倒过程特点，因此任意时刻的跌倒概率均为0。图3(d)～(f)是跌倒行为，跌倒发生后，身体失衡，之后与低势面碰撞，加速度数值剧烈变化并且出现跌倒点。当时间窗移动到该处，加速度观测序列满足了跌倒过程特点，因此时间窗内数据变化与跌倒模型的匹配程度增大，甚至概率曲线在某时段内为100%，表明这段数据完全符合跌倒过程。在跌倒点产生之后，身体接触地面，运动状态不再满足跌倒过程，因此与模型的匹配程度大幅降低。实验结果表明，基于隐马尔可夫模型进行跌倒检测的方法准确率高，并且具备优秀的特异性。Nyan等应用三轴加速度传感器与陀螺仪搭建了基于穿戴式设备的跌倒检测系统，方法检测的准确度为95.2%[7]；Li等使用加速度传感器与陀螺仪分析姿势体态进行跌倒检测，灵敏度为91%，特异性为92%[8]；王之琼等为基于极限学习机进行跌倒检测，准确度为93%，灵敏度为87.5%，特异性为91.7%[12]。对比这些研究，基于隐马尔可夫模型的跌倒检测方法不仅能保证95%以上的检测准确度，而且特异性表现十分突出，这意味着方法的误报率极低。分析其原因，隐马尔可夫模型表达了所描述时序过程的特点，跌倒模型兼顾了跌倒中加速度在时间与幅值上的变化特征，以检测加速度过程变化的方式判别跌倒，提高了特异性。验证实验结果表明，基于隐马尔可夫模型的跌倒检测方法检测效果优异。

4 结论

跌倒检测对保护老年人的健康及安全具有重要意义。本研究提出了一种基于隐马尔可夫模型对跌倒行为进行检测的新方法，分析了人体活动过程的加速度信息特点，采集了人体上躯干的加速度信息，并进行了观测序列的提取。将提取的、可代表跌倒过程的加速度观测序列作为训练样本，建立可描述跌倒过程的隐马尔可夫模型，把隐马尔可夫模型计算所得的输出概率作为跌倒风险的检测依据。实验结果表明，本方法可以准确检测出跌倒行为，并且能够有效区分跌倒过程与其他日常活动行为，其准确率达到98.2%，灵敏性达到91.3%，特异性达到99.6%。受到样本种类和数量的影响，本研究所训练的跌倒模型在实际应用中还需要进一步优化，验证实验的数据均以模拟老年人的运动方式进行采集，而真实情况下的老年人跌倒检测未能予以充分实验，这将是今后主要完善的工作。

[1] 朱月妹, 袁浩斌, 陈雷． 老年人跌倒危险因素的调查 [J]． 护理实践与研究, 2007, 4(10): 5-7.

[2] 郝燕萍, 刘雪琴, 靳海如． 老年人跌倒伤残情况分析 [J]． 护理研究, 2006, 20(8): 2017-2018.

[3] Rougier C, Meunier J. Demo: Fall detection using 3D head trajectory extracted from a single camera video sequence [J]. Journal of Telemedicine and Telecare, 2005, 11(4): 37-42.

[4] Shoaib M, Dragon R, Ostermann J. View-invariant fall detection for elderly in real home environment [C] //2010 Fourth Pacific-Rim Symposium on Image and Video Technology. Singapore: IEEE, 2010: 52-57.

[5] Qian Huimin, Mao Yaobin, Xiang Wenbo, et al. Recognition of human activities using SVM multi-class classifier [J]. Pattern Recognition Letters, 2010, 31(2): 100-111.

[6] Khan Z A, Sohn W. Abnormal human activity recognition system based on R-transform and kernel discriminant technique for elderly home care [J]. IEEE Transactions on Consumer Electronics, 2011, 57(4): 1843-1850.

[7] Nyan MN, Tay FE, Murugasu E. A wearable system for pre-impact fall detection [J]. Journal of Biomechanics, 2008, 41(16):3475-3481.

[8] Li Q, Stankovic JA, Hanson MA, et al. Accurate, fast fall detection using gyroscopes and accelerometer-derived posture information[C]//2009 6th International Workshop on Wearable and Implantable Body Sensor Networks. Berkeley: IEEE, 2009:138 - 143.

[9] Tong Lina, Chen Wei, Song Quanjun, et al. A research on automatic human fall detection method based on wearable inertial force information acquisition system [C] //2009 IEEE International Conference on Robotics and Biomimetics. Bangkok: IEEE, 2009: 949-953.

[10] Chen GC, Huang CN, Chiang CY, et al. A reliable fall detection system based on wearable sensor and signal magnitude area for elderly residents [C] //International Conference on Smart Homes and Health Telematics. Seoul: Springer, 2010: 267-270.

[11] Goh ATC. Back-propagation neural networks for modeling complex systems [J]. Artificial Intelligence in Engineering, 1995, 9(3): 143-151.

[12] 王之琼, 曲璐渲, 隋雨彤, 等. 基于极限学习机的跌倒检测分类识别研究 [J]. 中国生物医学工程学报, 2014, 33(4): 418-424.

[13] Li Yanjun, Chen Gan, Shen Yueyun, et al. Accelerometer-based fall detection sensor system for the elderly [C] //2012 2nd International Conference on Cloud Computing and Intelligence Systems. Hangzhou: IEEE, 2012, 3: 1216-1220.

[14] Sorvala A, Alasaarela E, Sorvoja H, et al. A two-threshold fall detection algorithm for reducing false alarms [C] //2012 6th International Symposium on Medical Information and Communication Technology. La Jolla: IEEE, 2012: 1-4.

[15] Dumitrache M, Pasca S. Fall detection algorithm based on triaxial accelerometer data [C] //2013 E-Health and Bioengineering Conference. Iasi: IEEE, 2013: 1-4.

[16] Bourke AK, O’brien JV, Lyons GM. Evaluation of a threshold-based tri-axial accelerometer fall detection algorithm [J]. Gait & posture, 2007, 26(2): 194-199.

[17] Yamato J, Ohya J, Ishii K. Recognizing human action in time-sequential images using hidden markov model [C] //1992 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Champaign: IEEE, 1992: 379-385.

[18] Lee KF, Hon HW. Speaker-independent phone recognition using hidden Markov models [J]. Acoustics, Speech and Signal Processing, IEEE Transactions on, 1989, 37(11): 1641-1648.

[19] Nathasitsophon Y, Auephanwiriyakul S, Theera-Umpon N. Fall detection algorithm using linear prediction model [C] //2013 IEEE International Symposium on Industrial Electronics. Taipei: IEEE, 2013: 1-6.

[20] Tong Lina, Song Quanjun, Ge Yunjian, et al. HMM-based human fall detection and prediction method using tri-axial accelerometer [J]. IEEE Sensors Journal, 2013, 13(5): 1849-1856.

[21] He Jin, Li Huanming, Tan Jindong. Real-time daily activity classification with wireless sensor networks using hidden markov model [C] //29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Lyon: IEEE, 2007: 3192-3195.

[22] 卢先领, 王洪斌, 王莹莹, 等. 一种基于加速度传感器的人体跌倒识别方法 [J]. 计算机应用研究, 2013, 30(4): 1109-1111.

[23] 佟丽娜, 宋全军, 葛运建. 基于时序分析的人体摔倒预测方法 [J]. 模式识别与人工智能, 2012, 25(2): 273-279.

[24] Rabiner LR, Juang BH. An introduction to hidden Markov models [J]. IEEE ASSP Magazine, 1986, 3(1): 4-16.

A Detection Method for the Fall Behavior of Elders Based on Hidden Markov Model

Cao Huiqiang1Lin Chungchih2Wu Shuicai1*

1(CollegeofLifeScienceandBio-engineering,BeijingUniversityofTechnology,Beijing100124，China)2(DepartmentofComputerScienceandInformationEngineering,ChangGungUniversity,Taoyuan33302,Taiwan,China)

As the social aging process quickened, the demand to care the elderly′s health and safety is increasing. The fall in the elderly population is a very common phenomenon; it has been a major health risk that diminishes the quality of life among the elderly people. In this paper, we proposed a new method using acceleration observation series to build a hidden Markov model (HMM)to detect the fall behavior. The method extracted acceleration characteristic time series from human fall course to describe the fall process, and used the acceleration characteristic time series to train HMM in order to build a random process mathematical model. The 300 samples of experimental data from 10 volunteers were obtained, and 5-fold cross-validation was used to estimate the model. Results showed that the accuracy of the method was 98.2%, the sensitivity was 91.3%, and the specificity was 99.6%, showing that the proposed method gets good result in detecting fall events.

fall detection; acceleration time series; hidden Markov model

10.3969/j.issn.0258-8021. 2017. 02.006

2016-04-18， 录用日期:2016-12-31

国家自然科学基金(71661167001)；台湾科技部科技研究项目(MOST 104-2218-E-182-005-MY3)

R318

A

0258-8021(2017) 02-0165-07

*通信作者(Corresponding author)，E-mail: wushuicai@bjut.edu.cn