基于表面肌电非负矩阵分解与一致性的肌间协同-耦合关系研究

谢 平 李欣欣 杨春华 杨芳梅 陈晓玲 吴晓光

(燕山大学电气工程学院河北省测试计量技术及仪器重点实验室，河北 秦皇岛 066004)

基于表面肌电非负矩阵分解与一致性的肌间协同-耦合关系研究

谢 平*李欣欣 杨春华 杨芳梅 陈晓玲 吴晓光

(燕山大学电气工程学院河北省测试计量技术及仪器重点实验室，河北 秦皇岛 066004)

肌肉协同模型是神经产生并控制运动的低维度结构，探讨不同动作任务下的表面肌电信号(sEMG)间的相干性分析，可以体现相应肌群的协同耦合关系，进而能从神经控制运动与肌肉相互配合协调的角度揭示运动产生与执行规律。组织8名年轻健康受试者(男女均半、20～24岁)进行上肢腕部屈、伸实验，采集动作时相应肌群的sEMG数据，引入非负矩阵分解(NMF)方法分析肌间协同性，并进一步对协同性较高的肌群采用一致性分析方法，研究信号beta(15～35 Hz)和gamma(35～60 Hz)频段的耦合强度关系，探讨腕部伸屈动作下不同受试者之间的协同-耦合性差异。结果表明：腕伸动作下，主动肌桡侧腕短伸肌(ECR)、指伸肌(ED)、尺侧腕伸肌(ECU)、肱桡肌(B)在协同模块W5中具有协同关系，且肌间耦合强度显著(P<0.05)，beta频段与gamma频段一致性显著面积相差较大(1.261±0.966)；腕屈动作下，分别在协同模块W1W4W5中存在具有协同关系的肌肉对，且肌肉间耦合强度显著(P<0.001)，在beta和gamma频段一致性显著面积相差较小(0.412±0.163)，但主动肌桡侧腕屈肌、指浅屈肌间不具有协同性，耦合关系较弱。以上说明：神经控制运动的方式不同，体现为肌肉协同-耦合关系有所差异；在同一协同模块中，协同性较高的肌肉间耦合关系较强，揭示神经控制运动规律与肌肉相互配合方式；运用此方法进行肌间协同-耦合联合分析，可望深入揭示中枢神经模块化协同控制运动机制，进一步为运动障碍患者功能分析和评价提供科学依据。

表面肌电；肌肉协同；肌间耦合；非负矩阵分解；一致性分析

引言

人体运动是一种由神经肌肉激活和生物力学输出产生的高复杂度活动[1]，在运动过程中，模块化结构常被用于解决肌肉间如何组织与协调多自由度变化的问题[2]。这种模块化结构定义多块肌肉共同作用形成激活模型，通过调节模型激活时间与强度来完成动作的“搭建”[3-4]，而在模型内部肌肉间同样存在依附与共同作用关系。因此，研究模块化结构中肌间关系特性，更有助于了解中枢神经系统(central nervous system, CNS)控制人体运动的产生、执行及协调方式。

中枢神经系统对肌肉的模块化分解被称为肌肉协同分析，不仅可以对存在协同作用的肌肉进行提取，而且能够获取反映肌肉激活的主要成分。针对以上特点，因子分解方法、主成分分析方法及非负矩阵分解(nonnegative matrix factorization, NMF)方法常被用于肌肉激活模式分析[5]、姿态时空特性分析[6]、脑电的相位空间重构[7]、能量谱特征提取[8]及腕部动作识别[9]等方面。以上分析方法均能从不同角度揭示神经从组织协调到运动执行的规律，但因子分解方法、主成分分析方法是将多指标转化为少数几个综合指标，降低了原始数据维度，而NMF方法的目的是将数据拆解成目标形式，且分解矩阵中所有元素均具有非负特性，使得分解形式和结果对肌肉激活具有更好的解释性。针对多通道肌电信号数据量大的特点，NMF方法能够简化数据形式，对目标信号实现简便、准确提取，因此更适合于协同分析。

肌肉协同作用可以反映多块肌肉的相互组合与协调关系，而两肌肉间的相互依附与共同作用关系，即耦合关系，可以从神经振荡传递运动控制信息角度反映肌肉间的功能联系[10-11]。计算肌间耦合特性的常用方法为一致性(coherence)分析方法，腕部屈伸运动研究发现，在姿势变化时肌间一致性也会相应调整[12]，运动过程中肌间耦合主要表现在beta(15～35 Hz)频段和gamma(35～60 Hz)频段[13]，beta频段的肌间耦合代表了从初级运动皮层到运动神经元的传递过程，而gamma频段振荡体现与认知功能相关的脑皮层信息整合过程[14]，各频段的肌间耦合分析为理解运动控制过程的组织与协调提供了理论基础。

过去研究侧重于单独的肌肉协同或肌间耦合分析，在神经控制运动方式[1]、肌肉间相互作用关系[13]以及神经通路与生物力学之间的相互影响[4]等方面分别做出阐述。肌肉协同的模块化结构是多块肌肉表达运动过程与运动目的方式，可以深入观察CNS生成的控制结构，D’Avella等早期研究发现，协同作用是肌肉多自由度问题的解决方案[2]，对于运动控制来说，CNS只需要控制较少的模块变量，就可控制众多的运动单元和肌肉。肌间耦合可在频段上分析协同模块的关联程度，并与生物力学运动相关联。肌间协同与耦合综合分析，可以从神经控制层面上探究肌间功能耦合关系与肌肉激活模型的关联程度，近期研究AMarchis C D等发现，下肢肌肉协同模块中部分肌肉间存在耦合关系[3]，在神经控制方面具有相互联系，仅发现肌间耦合在gamma频段中存在重要影响，对于肌肉协同性与肌间耦合特性之间具体关联关系并没有详尽阐述。

为进一步探索上肢不同运动下神经控制及运动协调机制，针对多通道表面肌电信号(surface electromyography, sEMG)的神经控制规律特性，探讨肌肉协同方式、肌间耦合强度及各频段上耦合强度差异性，本研究提出非负矩阵分解-一致性方法用于研究人体上肢腕部屈伸动作下肌间协同-耦合关系，从神经控制运动与肌肉相互配合协调的角度联合揭示运动的产生与执行规律，为深入分析人体运动的协调机制和控制规律提供研究方法和依据，为研究神经控制运动机理打下了基础。

1 实验数据采集及预处理

1.1 实验数据采集

受试者为8名(男4名，女4名)无上肢运动功能障碍或关节损伤历史的健康人。年龄20～24岁，体重47～75 kg，身高160～178 cm，均为右利手，无神经肌肉障碍[15]。所有受试者均自愿参加此测试，受试前24 h内未作剧烈运动，排除运动疲劳的影响。

sEMG采集采用DELSYS公司的表面肌电采集装置。实验记录两种腕部基本动作方式，即腕伸(wrist extension, WE)与腕屈(wrist flexion, WF)。sEMG信号采集带宽为5～450 Hz，采样频率为2 000 Hz。采用四点式银条采集表面肌电信号，电极顺着肌纤维方向粘贴。采集前先用酒精擦拭被测部位，去除皮肤表面油脂和皮屑。上臂支架，支撑上肢与身体成90°，如图1(a)所示。设备只允许前臂关节运动并约束肩膀来回摇摆，防止手臂疲劳对实验产生影响，对腕部运动没有任何辅助或阻力。在计算机上显示目标图像，以最大程度完成动作，初始状态和间歇状态均保持前臂放松。

同步采集右侧上肢8块肌肉sEMG信号，分别为指浅屈肌(flexor digitorum superficialis, FDS)、指伸肌(extensor digitorum, ED)、肱桡肌(brachioradialis, B)、桡侧腕屈肌(flexor carpi radialis, FCR)、掌长肌(palmarislongus, PL)、桡侧腕短伸肌(extensor carpi radialis, ECR)、尺侧腕伸肌(extensor carpi ulnaris, ECU)和肱二头肌(biceps brachii, BB)，采集位置如图1(b)所示。

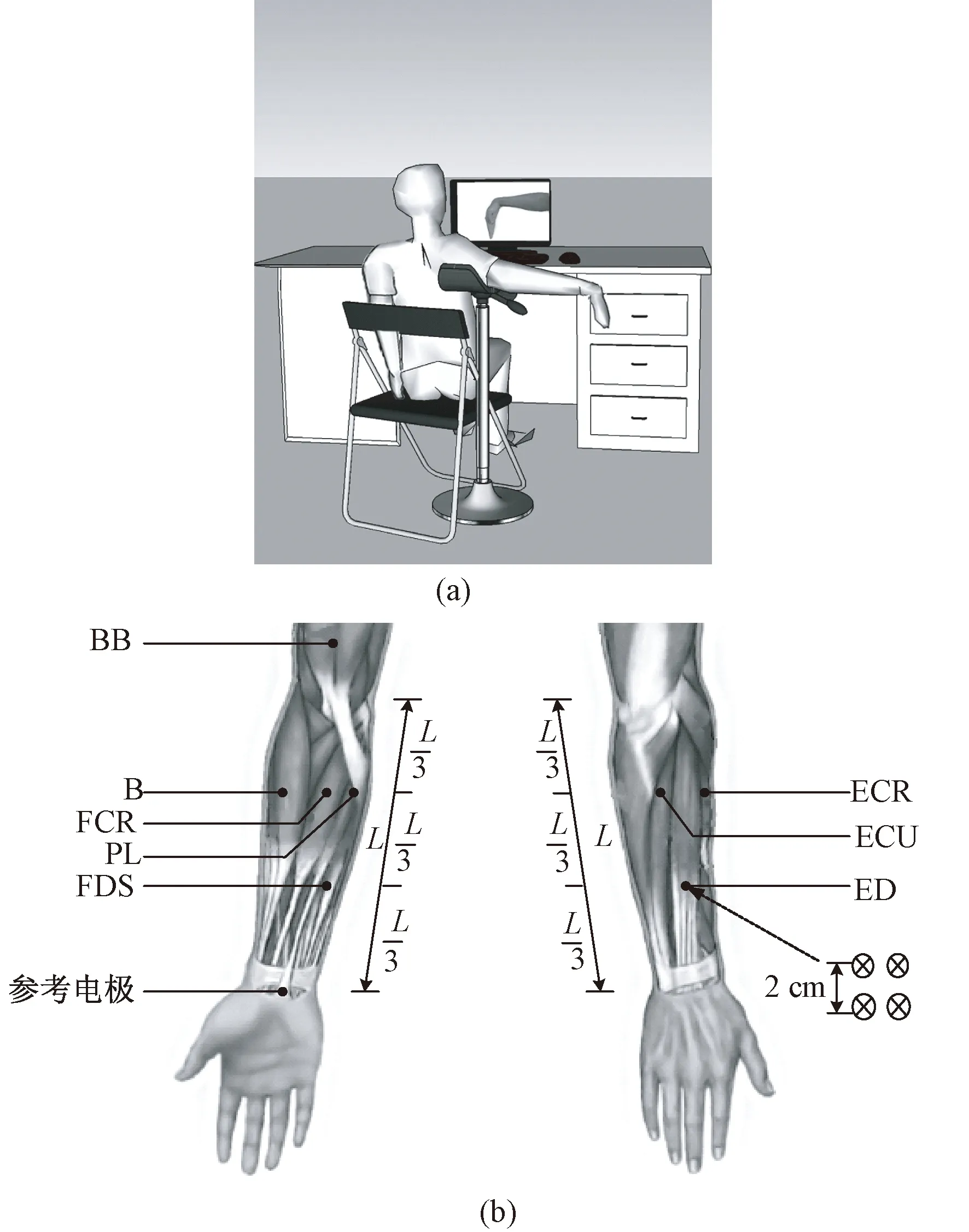
图1 上肢表面肌电信号采集实验。(a) 上肢摆位与腕部运动；(b) 腕部屈伸运动相关肌肉与表面肌电采集位置Fig.1 Experimental on sEMG signal acquisition of upper limbs. (a) Upper limb position and wrist motion; (b) Wrist flexion - extension related muscle and sEMG signal acquisition position

1.2 肌电信号预处理

根据动作演示(见图1)，设置动作图片显示时间为4 s，动作切换间歇时间为3 s。在处理数据过程中，去除有效数据中的前0.5 s与后0.5 s，保证在中间过程中手腕保持静止。为了更好地分析数据，获得有效的sEMG信号特征，需对原始信号进行预处理。首先，对信号做去均值处理，并用于一致性分析，以避免带通处理对信号造成影响，保证低频波段的真实有效性[16-17]；然后，进行低通与高通滤波(截止频率为4、200 Hz)，整流后提取信号包络；最后，对处理后的信号进行最大值归一化，用于肌肉协同分析。

1.3 非负矩阵分解-一致性分析方法

为研究协同肌肉间耦合特性，本研究提出非负矩阵分解-一致性分析方法应用于上肢腕部屈伸动作的肌电信号分析中。先应用非负矩阵分解方法来确定肌肉协同结构，得到协同性较强的肌肉对，并结合一致性方法计算协同性肌肉间的耦合强度。

1.3.1 基于非负矩阵分解的肌肉协同分析

针对肌肉激活模式中的非负与模块化的概念，采用非负矩阵分解(NMF)算法[18]提取肌肉协同。NMF通过发掘数据之间的内在关系获得映射矩阵，再把高维数据投影到低维子空间中，从而达到聚类、降维等目的。NMF算法的形式为

(1)

式中：Wiα为基矩阵，Hαμ为系数矩阵，n为基矩阵分解列数；原矩阵Viμ的列向量可以解释为Hαμ中所有列向量的加权和，而权重系数为Wiα中对应列向量中的元素。

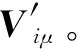
基于非负矩阵分解方法对肌电信号建立肌肉协同模型，如图2所示。具体过程如下，构建三通道肌电原始信号矩阵Viμ，其中i=3为信号个数，μ为0.5s时间内的采样点数，如图2(a)所示，当分解列数n=2时，分解得到肌肉协同矩阵W32、激活尺度系数矩阵H2μ，如图2(b)所示。并对两个分解矩阵进行重构，得到重构矩阵V′iμ，如图2(c)所示。

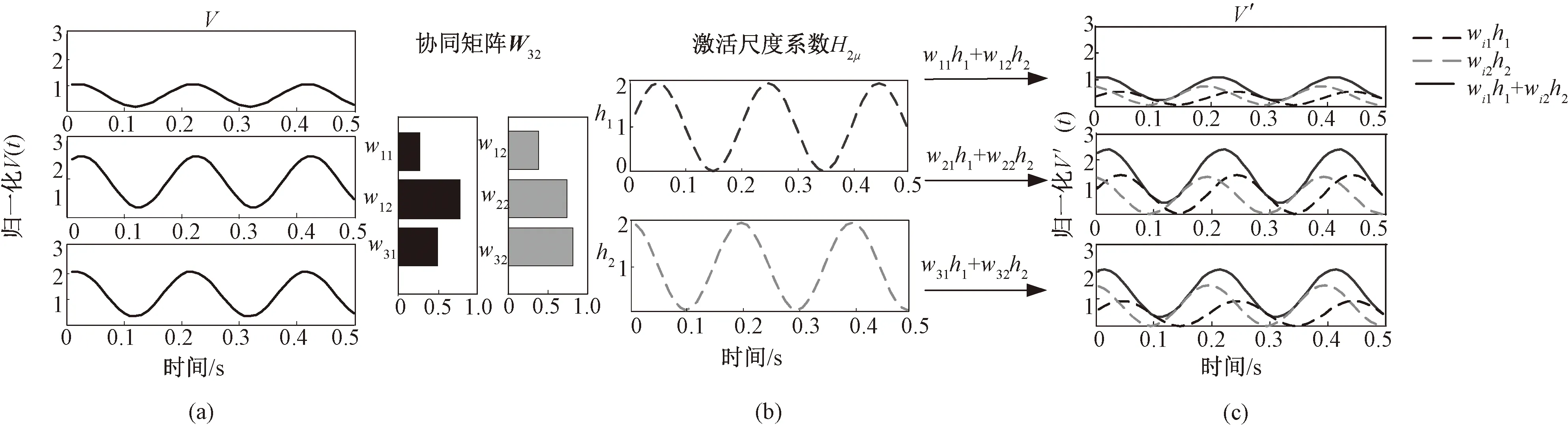
图2 基于非负矩阵分解方法的肌肉协同模型。(a) 模拟肌电信号模型；(b) 协同模型；(c) 肌电重构模型Fig.2 The synergy model of muscles based on the nonnegative matrix factorization method. (a) Simulated sEMG signal model; (b) Synergy model; (c) sEMG reconstruction model

为确定上述分解过程中肌肉协同矩阵列数n，即基矩阵分解列数，运用解释方差(variabilityaccountedfor,VAF)[19]计算方法，定义如下：

(2)

式中，RSS为残差平方和(residualsumofsquares,RSS)，TSS为总平方和(totalsumofsquares,TSS)，Viμ是原始肌肉激活模式矩阵，V′iμ是NMF算法重构后的数据矩阵。

经过不断迭代计算，通过VAF值来判断分解模型准确程度，在n较小情况下，VAF值较低，此时的分解模型仅涵盖原始信号部分有用信息，Clark等[20]研究发现，当分解模块数少时，其分解出的模块是许多模块的叠加，且不足以表现原始信号信息。认为当VAF值大于92%，且随着n值的增加VAF增加小于2%时，此时n为有效分解列数。为更好地表现重构信号的细节，对原始信号有用信息尽量保留，当协同模块数目为n=5，满足上述条件，从而确定协同结构。

1.3.2 基于一致性分析方法的协同肌肉耦合强度分析

根据本文第1.3.1节非负矩阵分解方法得到的肌肉协同模式，对协同性较强的肌肉对进行耦合强度分析。两肌电信号x、y在频率λ处的Coherence计算公式为

(3)

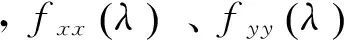
信号间一致性程度可用显著一致性阈值S描述[21]，计算公式为

(4)

式中：n表示参与谱估计的数据段数目；α为置信水平(α=0.95)，超过显著性阈值P<α时两肌电相干显著。

为了比较组间一致性，本研究提出一致性面积指标AC，即一致性曲线与一致性阈值S之间区域面积，用来描述各频段不同受试者之间的统计差异，有

(5)

式中：Δλ表示频率分辨率；AC的数值越大，表示协同性肌肉间耦合强度越高。

2 结果

在不同的运动状态下，肌肉协调与激活方式有所不同，所以对腕屈腕伸动作下肌肉进行协同-耦合分析，即采用本文第1.3.1与1.3.2节中非负矩阵分解-一致性方法，分析本文第1.1节采集并经过本文第1.2节预处理后的肌电信号。

2.1 腕伸(WE)动作下肌肉协同-耦合分析

提取腕伸动作肌电活动段数据，并进行协同肌肉间的耦合强度分析，得到腕伸动作的分解协同模块与激活尺度系数关系(见图3(a))，对具有协同作用的肌肉对进行一致性分析得到曲线(见图4(a))，并对非协同性肌肉对进行一致性分析得到曲线(见图4(b))。

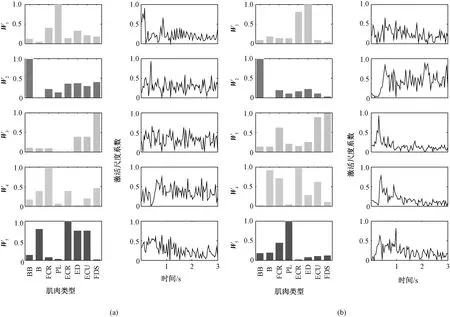
图3 各动作下的平均肌肉协同模型(左列为协同模型，右列为激活尺度系数)。(a)腕伸动作；(b) 腕屈动作Fig.3 The average synergy model of under each movement (The left column is the synergy model and the right column is the activation scale factor). (a) Synergy model of wrist extension; (b) Synergy model of wrist flexion

由图3(a)可见，在腕伸动作下，ECR(桡侧腕长伸肌)、ED(指伸肌)、ECU(尺侧腕伸肌)、B(肱桡肌)在协同模块W5中具有协同关系，其他模块中肌肉间协同关系不明显。为了更好地对比观察协同性肌肉于非协同肌肉的一致性关系，笔者选择6块不具有协同性的肌肉进行对比分析。具有协同性的肌肉一致性分析如图4(a)所示，不具有协同性的肌肉对一致性分析如图4(b)所示。由图可见，具有协同性的肌肉耦合强度较强，而不具有协同性的肌肉其一致性曲线仅在显著性阈值左右变化。

图4 腕伸WE动作下肌间一致性。(a)具有协同性肌肉间一致性；(b)非协同性肌肉间一致性Fig.4 Intramuscular coherence in wrist extension movement. (a)Coherence between strong synergy muscles; (b)Coherence between uncooperative muscles

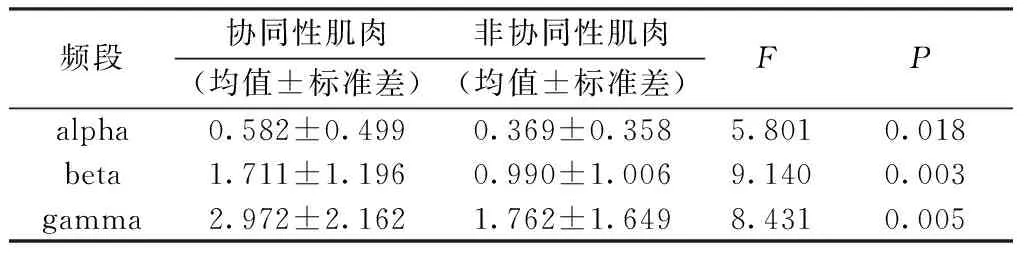
对上述一致性分析结果，利用显著性面积公式(见式(5))，计算所有被测者alpha(8～15Hz)、beta(15～35Hz)、gamma(35～60Hz)频段的显著性面积AC。WE动作下，图4(a)中所有协同性肌肉对与图4(b)中非协同肌肉对平均显著性面积比较如表1所示。可见，协同性肌肉与非协同性肌肉间的组间显著性水平P<0.05，因此可认为协同性与否对肌间一致性在各频段的显著性面积有显著影响，置信度为95%。协同性肌肉一致性显著面积在beta频段与gamma频段相差为1.261±0.966，在gamma频段显著性更明显。

表1 WE动作下协同关系的显著性面积比较

Tab.1 The significant area of synergistic function measures ANOVA of WE movement

频段协同性肌肉非协同性肌肉(均值±标准差)(均值±标准差)FPalpha0.582±0.4990.369±0.3585.8010.018beta1.711±1.1960.990±1.0069.1400.003gamma2.972±2.1621.762±1.6498.4310.005

2.2 腕屈(WF)动作下肌肉协同-耦合分析

同样，与本文第2.1节相似，得到分解协同模块与激活尺度系数关系(见图3(b))和具有协同性的肌间一致性分析曲线(见图5(a))，以及不具有协同性的肌肉的肌间一致性分析曲线(见图5(b))。

由图3(b)可见，在腕屈动作下，W1模块中具有协同性的肌肉为ED-ECR；W4模块中有ECR-B、B-FCR、FCR-ECU、B-ECU，W5模块中有FCR-PL。观察图5(a)、(b)可见，具有协同性的肌肉，肌间耦合强度较强，而非协同性肌肉，肌间耦合强度相对较弱。

同样，利用显著性面积公式(见式(5))，计算所有被测者alpha、beta、gamma频段的显著性面积AC。WF动作下，图5(a)中所有协同性肌肉对与图5(b)中非协同肌肉对的显著性面积比较如表2所示。

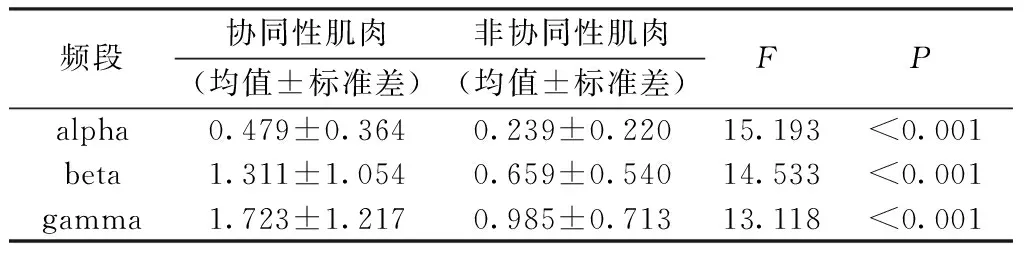
表2 WF动作下协同关系的显著性面积比较

Tab.2 The significant area of synergistic function measures ANOVA of WF movement

频段协同性肌肉非协同性肌肉(均值±标准差)(均值±标准差)FPalpha0.479±0.3640.239±0.22015.193<0.001beta1.311±1.0540.659±0.54014.533<0.001gamma1.723±1.2170.985±0.71313.118<0.001

由表2可见，协同性肌肉与非协同性肌肉间的组间显著性水平P<0.001为极显著统计差异性，因此可以认为协同性与否对肌间一致性在各频段的显著性面积有显著影响。协同性肌肉一致性显著面积在beta频段与gamma频段相差为0.412±0.163，在beta与gamma频段显著性差异不明显。

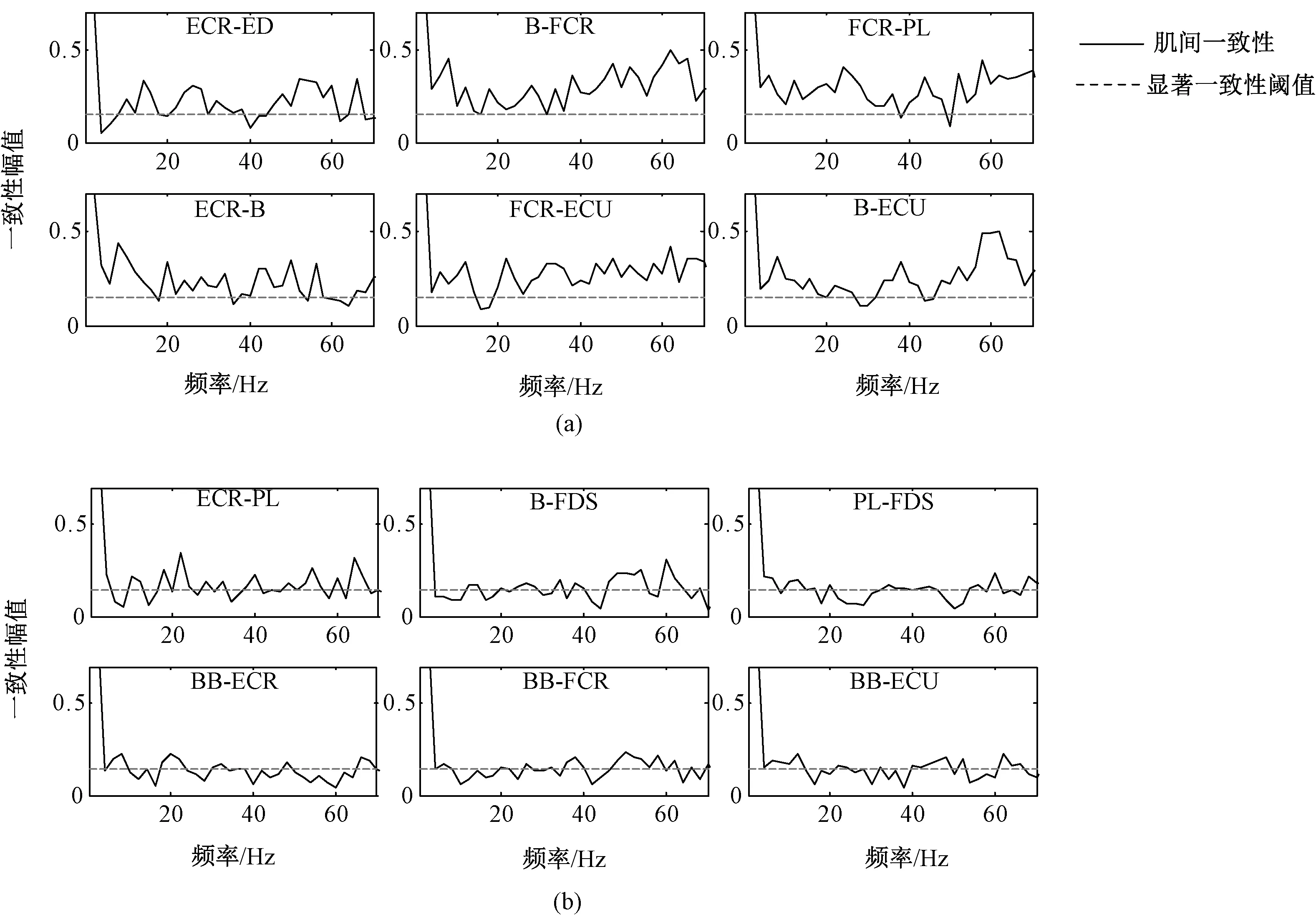
图5 腕屈WF动作下肌间一致性。(a)具有协同性肌肉间一致性；(b)非协同性肌肉间一致性Fig.5 Intramuscular coherence in wrist flexion movement. (a)Coherence between strong synergy muscles; (b)Coherence between uncooperative muscles

3 讨论与结论

从上肢摆位与腕部运动示意图1(a)中可看出，肱二头肌作用为支撑前臂，与其他肌肉功能有所不同，图3中腕屈与腕伸动作的共享协同模块W2中肱二头肌比重最高，其他肌肉相对较低，从而印证协同模块分解能够将共同作用肌群划分出来，对中枢神经系统模块化控制肢体运动的假设提供依据。

从上述两种动作下的肌间协同-耦合分析结果可见：腕屈与腕伸动作下都具有其特殊的协同模块，并与共享协同模块W2共同作用，从而产生灵活多样的运动方式。在腕伸(WE)动作下，主动肌主要为ECR(桡侧腕长伸肌)、ED(指伸肌)、ECU(尺侧腕伸肌)，如图3(a)所示，在W5模块中，上述肌肉所占比重较高，相互间具有协同性，产生共同作用，且根据图4(a)中上述肌肉两两间存在耦合关系，表明该动作下CNS是通过相同的神经元信息来控制伸肌完成动作。在腕屈(WF)动作下，主动肌主要为FCR(桡侧腕屈肌)、FDS(指浅屈肌)，如图3(b)所示。未在分解模块中发现上述肌肉同时比重较高地分布在同一模块中，肌肉之间不具有协同性，且根据图4(b)中上述肌肉间耦合强度相对较低，表明该动作下神经控制屈肌通过单独指令完成，以避免出现肌肉间混连发生。由此可知，在不同动作下，神经控制运动的编码方式有所不同，使得肌肉间形成不同的组合方式，并通过肌肉间相互配合协调，从而形成不同动作[4]。

进一步发现，在同一模块中具有协同性的肌肉对的肌间耦合强度明显高于非协同性肌肉(见图4、5)，主要表现在beta频段与gamma频段中(见表1、2)。神经控制运动的神经元传递信息大部分存在beta频段[18,23-24]。在腕伸(WE)动作下，beta频段与gamma频段显著性面积AC均值相差较大。研究发现：在适中的肌力输出情况下，肌间耦合强度会在beta频段明显增强；在较大肌力输出时，同步频率会向高频移动，出现在gamma频段[10]。在执行腕伸动作时，比腕屈动作需更大的肌力输出，其肌间耦合强度在gamma频段较强。Marchis等研究同样发现，在gamma频段中存在肌间耦合关系[3]，其可能与力量的增大与维持有关。

综上所述，本研究将非负矩阵分解和肌间一致性分析方法相结合，应用于上肢不同动作下的表面肌电信号分析，不仅可以有效分解具有协同关系的活动肌群，也可进一步得到肌群内部肌肉间的协同-耦合关系，为探究神经控制运动的肌肉协调与分工协作方式提供研究方法和依据。结果表明，在上肢屈伸动作下，肌肉协同方式体现为具有相似功能的模块，且协同性强的肌肉间耦合关系较强，主要表现在beta频段与gamma频段。笔者关于肌间协同-耦合关系的研究，验证了中枢神经系统的模块化控制假设，并从神经控制运动与肌肉相互配合协调的角度联合揭示运动的产生与执行规律，为深入研究神经控制运动机理提供了依据，也对运动功能定量分析和评价提供了新方法。

(致谢：感谢实验工作人员刘欢、邱石在研究工作中给予支持。)

[1] Gottlieb GL. Muscle activation patterns during two types of voluntary single-joint movement [J]. Journal of Neurophysiology, 1998, 80(4): 1860-1867.

[2] D’Avella A, Tresch M. Muscle Synergies for Motor Control [M]// Handbook of Neural Engineering. Hoboken: MA kay wiley, 2006: 449-465.

[3] Marchis CD, Severini G, Castronovo A M, et al. Intermuscular coherence contributions in synergistic muscles during pedaling [J]. Experimental Brain Research, 2015, 233(6): 1907-1919.

[4] Geyer H, Herr H. A muscle-reflex model that encodes principles of legged mechanics produces human walking dynamics and muscle activities [J]. IEEE Transactions on Neural Systems & Rehabilitation Engineering, 2010, 18(3): 263-273.

[5] Russo M, Dandola M, Portone A, et al. Dimensionality of joint torques and muscle patterns for reaching [J]. Frontiers in Computational Neuroscience, 2014, 8(3): 24.

[6] Tresch MC, Jarc A. The case for and against muscle synergies [J]. Current Opinion in Neurobiology, 2009, 19(6): 601-607.

[7] Ivanenko YP, Poppele RE, Lacquaniti F. Five basic muscle activation patterns account for muscle activity during human locomotion [J]. The Journal of Physiology, 2004, 556(1): 267-282.

[8] Torresoviedo G, Ting LH. Muscle synergies characterizing human postural responses [J]. Journal of Neurophysiology, 2007, 98(4): 2144-2156.

[9] 张启忠，席旭刚，马玉良，等. 基于表面肌电信号的手腕动作模式识别 [J]. 中国生物医学工程学报, 2013, 32(3): 257-265.

[10] d’Avella A, Portone A, Fernandez L, et al. Control of fast-reaching movements by muscle synergy combinations [J]. The Journal of Neuroscience, 2006, 26(30): 7791-7810.

[11] De MC, Castronovo AM, Bibbo D, et al. Muscle synergies are consistent when pedaling under different biomechanical demands [C]// International Conference of the IEEE Engineering in Medicine & Biology Society. Conf Proc IEEE Eng Med Biol Soc, 2012: 3308-3311.

[12] Keenan KG, Massey WV, Walters TJ, et al. Sensitivity of EMG-EMG coherence to detect the common oscillatory drive to hand muscles in young and older adults [J]. Journal of Neurophysiology, 2012, 107(10): 2866-2875.

[13] Jesunathadas M, Laitano J, Hamm TM, et al. Across-muscle coherence is modulated as a function of wrist posture during two-digit grasping [J]. Neuroscience Letters, 2013, 553(8): 68-71.

[14] 谢平，宋妍，郭子晖，等. 中风康复运动中肌肉异常耦合分析 [J]. 生物医学工程学杂志, 2016, 33(2): 244-254.

[15] Patino L, Omlor W, Chakarov V, et al. Absence of gamma-range corticomuscular coherence during dynamic force in a deafferented patient [J]. Journal of Neurophysiology, 2008, 99(4): 1906-1916.

[16] Ting LH, Mckay JL. Neuromechanics of muscle synergies for posture and movement [J]. Current Opinion in Neurobiology, 2007, 17(6): 622-628.

[17] Lee DD, Seung HS. Learning the parts of objects by non-negative matrix factorization [J]. Nature, 1999, 401(6755): 788-791.

[18] Gopalakrishnan A, Modenese L, Phillips AT. A novel computational framework for deducing muscle synergies from experimental joint moments [J]. Frontiers in Computational Neuroscience, 2014, 8: 153.

[19] Kattla S, Lowery MM. Fatigue related changes in electromyographic coherence between synergistic hand muscles [J]. Experimental Brain Research, 2010, 202(1): 89-99.

[20] Brach P, Alessander DS, Mark J, et al. Force-independent distribution of correlated neural inputs to hand muscles during three-digit grasping [J]. Journal of Neurophysiology, 2010, 104(2): 1141-1154.

[21] Clark DJ, Ting LH, Zajac FE, et al. Merging of healthy motor modules predicts reduced locomotor performance and muscle coordination complexity post-stroke [J]. Journal of Neurophysiology, 2010, 103(2): 844-857.

[22] Fisher KM, Zaaimi B, Williams TL, et al. Beta-band intermuscular coherence: a novel biomarker of upper motor neuron dysfunction in motor neuron disease [J]. Brain A Journal of Neurology, 2012, 135(9): 2849-2864.

[23] Farmer SF, Swash M, Ingram DA, et al. Changes in motor unit synchronization following central nervous lesions in man [J]. Journal of Physiology, 1993, 463(12): 3364-3377.

[24] Norton JA, Wood DE, Marsden JF, et al. Spinally generated electromyographic oscillations and spasms in a low-thoracic complete paraplegic [J]. Movement Disorders, 2003, 18(1): 101-106.

Research on the Intermuscular Synergy and Coupling Analysis Based on Surface EMG Nonnegative Matrix Factorization-Coherence

Xie Ping*Li Xinxin Yang Chunhua Yang Fangmei Chen Xiaoling Wu Xiaoguang

(KeyLabofMeasurementTechnologyandInstrumentationofHebeiProvince,YanshanUniversity,Qinhuangdao066004,Hebei,China)

The muscle synergy model is a low-dimensional structure in which nerves produce and control motion. The aim of this work was to study whether the coherence of surface electromyography could reflect the synergy-coupling relationship of the muscle groups under different movements and reveal the laws of movement generation and execution from the point of neural control and muscle coordination. In this study, we chose eight young healthy subjects (4 men and 4 women, 20～24 years old) to perform the upper limb wrist flexion and extension experiments, the sEMG data from different muscle groups were collected during the action. This study analyzed synergy between muscles by nonnegative matrix factorization. The coherence analysis method was used to study intermuscular coupling relationship in the beta (15～35 Hz) and gamma (35～60 Hz) band with the signals of high synergy muscles, and the differences of synergy-coupling between different subjects under wrist flexion and extension were investigated. Results showed that active muscles of extensor carpi radialis (ECR), extensor digitorum (ED), extensor carpi ulnaris (ECU) and brachioradialis (B) had synergistic relationship in synergy modelW5under the wrist extension movement, the intensity of intermuscular coupling was significantly different (P<0.05), and there was a significant difference in the value of coherence area between beta and gamma band (1.261±0.966). In the wrist flexion movement, intermuscular synergy appeared in synergy modelsW1W4W5， the intensity of intermuscular coupling was significantly different (P<0.001), and there was a nuance in the value of coherence area between beta and gamma band (0.412±0.163), active muscles of flexor carpi radialis (FCR) and flexor digitorum superficialis (FDS) had no synergistic relationship, the intermuscular coupling relationship was small. Taken above together, there were differences in the neural control action, which showed the different intermuscular synergy-coupling relationship. In the same synergy model, the intermuscular coupling relationship with high synergism was stronger. It revealed the law of the neural control action and muscle interaction with each other. The proposed method was expected to be applied in the future to reveal the central nervous system of modular synergistic control mechanism of movement, and to provide scientific basis for functional analysis and evaluation of patients with movement disorders.

sEMG; muscle synergy; intermuscular coupling; nonnegative matrix factorization; coherence analysis

10.3969/j.issn.0258-8021. 2017. 02.004

2016-07-27， 录用日期:2016-11-05

国家自然科学基金(61271142，61503325)；河北省自然科学基金(F2015203372)

R318

A

0258-8021(2017) 02-0150-08

*通信作者(Corresponding author)，E-mail: pingx@ysu.edu.cn