基于ESEM的高阶思维结构测量模型研究
姜玉莲 解月光

摘要:新技术、新媒体的发展使人类前所未有地减轻了低阶知识与能力的负荷,对于21世纪的公民而言,更需要具备完成复杂任务、解决劣构问题的高级综合能力,即高阶思维(Higher-Order Thinking)。高阶思维结构具有整体性、发展性、社会性、复杂性和难以测评性。当前已有的各种与高阶思维能力相关的测量量表,虽然能对高阶思维某一方面的傾向性或行为过程做出一定的评价,但缺乏对课堂教学情境中高阶思维发展过程及其能力的整体性评价和操作性指导,更忽略了对同伴情感支持、自我效能感和自我调节等非智力因素在高阶思维发展中的观测。因此有必要从课堂情境出发,探究高阶思维结构的测量模型。通过探索性结构方程建模(ESEM)形成的高阶思维结构模型,包括创造性策略、问题解决过程以及批判性调节学习3个二阶因素,以及创新性思维、决策能力、元认知与反思性评价、问题解决能力、同伴情感支持、自我效能感、批判性思维、自我调节学习等8个一阶因素。该模型不仅关注思维技能与问题解决能力的行为特征,还考虑了情感与动机的作用。这对于全面认识高阶思维发展过程与活动的整体性具有一定的价值。
关键词:高阶思维结构;课堂情境;因素分析;ESEM;测量模型
中图分类号:G434 文献标识码:A 文章编号:1009-5195(2017)03-0094-11 doi10.3969/j.issn.1009-5195.2017.03.012
一、问题提出
近年来,数字化给传统教育体系带来巨大冲击,大量记忆性和检索性工作被信息技术所代替,高阶思维(Higher-Order Thinking)作为完成复杂任务、解决劣构问题的高级综合能力(钟志贤,2004),在世界各国国家战略与学习研究中都受到了前所未有的重视。
高级思维技能是在思维过程、思维策略和具体问题情境中逐渐养成的。深层次学习、问题解决、良好的思维品质以及思维的自我监控等智力与非智力因素之间的相互作用是高阶思维形成的过程。反映在课堂教学情境中,就是具体的教与学活动。那么,课堂情境作为学生高阶思维发展的重要场所,怎样才能使学生的高阶思维潜能得到很好的发展呢?布鲁姆思维类型分类系统中,将分析、综合、评价作为高阶思维(王帅,2011)。虽然这种分类为具体的教学实践提供了便利的图式,但实际上思维与其他客观现实世界的事物和现象一样,具有客观世界的整体性、复杂性和统一性,也就决定了人的思维是一个系统性结构。林崇德教授(2007)在系统科学、结构主义、辩证唯物主义理论基础上构建了思维结构系统模型,并认为人体之间智力差异的根本原因在于思维结构的差异。只要解决了人类思维结构的问题,人类智力的种种问题都可以迎刃而解。高阶思维作为具体思维发展到抽象思维的高级综合能力的具体体现,也应该从整体性出发进行探索。因此,高阶思维结构的研究可以使人们更深入地了解高阶思维系统内各组成要素之间相互联系、相互作用的方式以及存在、运动的状态与发展变化,更好地促进课堂情境中高阶思维问题的探索。
国内外一些学者对思维和创新性思维做了因素结构论、维度结构论、认知结构论、系统结构论、发展阶段论等方面的探索,形成了“智力三维结构”“创造力三维模型理论”“布鲁姆教育目标分类学”“思维系统结构”“皮亚杰儿童阶段发展论”等经典理论,但目前针对高阶思维结构的研究还是寥寥无几,大多是从问题解决、创新性思维、批判性思维等角度间接地讨论高阶思维问题,或者把元认知、批判性思维、问题解决、创造性思维等同于高阶思维。这些研究大都是从高阶思维发展的某个角度提出的,体现了个体对问题情境的适当反应过程,以及高阶思维发展过程中某方面的倾向性或某个行为的过程,并不代表高阶思维的整个活动。同时在研究方法上,已有探索也更多地是停留在价值、意义的描述上,缺乏具体的流程设计和深入的实证分析。在实践应用中,虽然出现了“托兰斯创造性思维测验”等高级思维能力测量量表,但更多的是关注思维整体能力的评价,对于具体的课堂情境实践指导并没有实质性推进。
高阶思维作为课堂教学活动中学习者高水平的认知能力或心智活动,其结构很难测量,但可以通过深层次学习、问题解决、意义建构等高级认知活动以及良好的思维品质与自我调节等智力与非智力因素之间的相互作用,来进行高阶思维行为、情感及高阶思维品质特点的识别(Rupert Wegerif,2009)。而且,高阶思维发展过程是将问题知识进行有意义建构的过程。通过高阶知识信息的输入、学习过程体验和反馈评价等系统化过程,可以使高阶思维发展目标实现以学习者外显行为来表现。也就是说,高阶思维系统属性决定了高阶思维的行为不是一个孤立的领域,而是由认知、情感、动作的共同整合,即高阶思维学习过程始终都是学习者依据自身知道什么、能做什么和对情境有什么样的感受来表现其行为的。反映在教学系统结构和行为特征中,是从行为“统整”角度将行为与智慧、情感和动作技能等领域进行路径的整合,以培养具有高阶知识、智慧性情操和高阶思维能力胜任力的人(盛群力,2008)。基于此,本文采用因素分析法,通过对课堂情境中高阶思维过程、策略与问题的行为统整表征、状态描述等直接观测指标的设定,萃取出能反映高阶思维结构要素之间内在联系、本质特征的潜在变量,为课堂教学情境中高阶思维的培养和设计提供实证性借鉴。
二、研究设计
1.研究方法
由于研究之前并不能明确所设计的高阶思维结构观测变量和因子之间潜在的关系结构,因此笔者采用因素分析法对已获得的数据进行降维处理,在确定潜在公因子的基础上再建立高阶思维结构因子模型。探索性因子分析可以寻找公因子来达到降维、简化结构的目的,但缺乏对实际数据与理论模型拟合情况的检验。因此,我们利用了探索性结构方程建模(ESEM)。该方法既能灵活地探索高阶思维的因子结构,又可以系统地验证因子模型的功能与优点,为高阶思维结构潜变量之间的关系分析提供更适宜的测量模型(麦玉娇等,2013)。在因子分析与萃取过程中,考虑到高阶思维结构的复杂性与整体特征以及各因素间的相关性,因素分析方法采取能生成相关矩阵的极大似然法。因子萃取采用斜交转轴法中的Promax(又称为最优斜交法),以使因子相关联。
2.问卷设计与样本调查
(1)问卷设计
目前从课堂情境视角直接进行高阶思维过程、策略与问题情境评价的量规并不多见。本研究根据前期文献分析和课堂实际观察,发现“推理策略”“问题解决方法”“决策技能”“高级思维技能”“批判性思维”“创造性思维”等思维策略与高阶思维能力之间具有密切的联系。因此,在进行高阶思维结构问卷设计时,我们主要利用课堂情境中“高阶思维与问题解决”“创造性思维”“批判性思维”以及“分析、判断、推理、决策”认知过程等具体行为与活动外在表征来间接评定学生的高阶思维水平。同时,我们也综合考虑了情感、价值观、社会支持等非智力因素在思维发展中的重要性,尤其是“自我调节”“自我效能”“同伴情感互助”对高阶思维发展的促进。
在具体设计中,我们参照国内外心理学及教育专家从元认知、问题解决能力、创造性思维、批判性思维以及自我调节、自我效能感等各个视角进行的高阶思维过程与能力研究,如Borich和Tombari对美国中小学设计的《高级思维和问题解决核查表》,余平教授在此基础上针对中国课堂教学设计的《创造力及高层次思维能力的行为表现量表》和《创造性思维策略使用核查表》,美国学者Montgomery的《问题解决量规》、黄茂在等设计的《问题解决能力的评分指标》等(余林,2007;Robert L. Linn等,2003)。除此之外,我們还借鉴了《加利福尼亚批判性思维倾向》、方平教授的《自我调节学习量表》、Schwarzer《自我效能量表》中的行为倾向、情感参与及感受的观测指标。依据高阶思维的智力因素、非智力因素、思维发展及社会化认知理论等,我们形成了《高阶思维结构行为表征与情感体验核查表》,主要包含动机与自我效能感、自我学习调节与控制、同伴问题解决活动、创造性思维与迁移能力、批判性思维倾向、问题解决策略与能力、判断与决策能力等160项观测指标。为了使观测指标更加科学化,我们选择了北京市中小学校各一所进行预研究并组织中小学教师与相关学者进行专家会议论证。根据预研究回收的89份问卷与数据分析,删掉观测指标12项;根据专家会议又删掉了18项观测指标。最后调整得到的高阶思维结构观测指标共130项,均采用六级李克特量表计分,其中“1”代表“非常不认同”,“2”代表“不认同”,“3”代表“部分不认同”,“4”代表“部分认同”,“5”代表“认同”,“6”代表“非常认同”。
(2)样本调查
在课堂实地听课和访谈的基础上,我们按照分层随机抽样方法,选择发达地区、中等发达城市、县级城市、乡镇,对北京市区、山东青岛市区、山东济宁地区(梁山县城、曲阜乡镇)、江苏无锡与泰州地区、长春市区6个地区,12所不同年级、不同发展水平的中小学,进行问卷发放。问卷发放均采取了课堂现场填写与回收方式。本次研究共回收问卷1565份,有效问卷1505份。总样本被随机分成两类独立样本。其中656份样本做探索性因素分析,男女生各占44.97%与55.03%,年级与地区分布如图1、图2。另外849份样本做ESEM与验证性因素分析,男女生各占48.4%与50.5%,缺失值占1.1%,年级与地区分布如图3、图4。两类独立样本的男女比例、年级与区域分布基本均衡。
(3)样本检验
在具体分析之前,我们对两类独立样本分别进行了正态分布检验、信度与效度检验。正态分布检验可以更好地选择因子旋转方法,信度检验反映的是问卷测量所得结果的一致性和稳定性,效度检验反映了问卷测量所得结果的准确性和有用性。
对于样本的正态性检验,我们选用偏度峰度检验法。经检验,两类独立样本的偏度系数和峰度系数绝对值大部分均小于 1,极个别小于 2,偏度系数和峰度系数具有显著性,基本符合正态性分布。信度检验选择Cronbach's Alpha信度系数进行检验,结果发现Cronbach's Alpha信度系数在0.9以上,问卷的信度非常好,稳定性和内在一致性非常高(Dimiter M. Dimitrov,2015)。效度检验主要是对内容效度和结构效度进行分析。由于在问卷编制过程中,已经对测验项目与所涉及的内容范围进行了符合性判断;且通过专家会议法对问卷内容进行评价,因此,问卷的测量内容及范围的科学性和准确性已经得到验证。结构效度采取的是KMO(取样适当性)和巴特利特球形检验。结果发现:探索性因素分析样本KMO(取样适当性)=0.961,Bartlett's(8256)=37149.197,p<0.001,量表非常适合因素分析;验证性样本KMO=0.989,p<0.001,达到了显著性水平。
3.工具选择与统计分析过程
ESEM是在测量模型部分使用了类似于 EFA 模型的 SEM因子分析方法。目前在EFA应用较多的是SPSS,ESEM支撑比较良好的工具是Mplus。因此我们在研究中综合使用了SPSS的探索性因素分析和Mplus的探索性结构模型(ESEM)。具体作法是:首先,通过SPSS工具对高阶思维结构进行探索性因素分析,初步确定高阶思维因子数目;其次,通过Mplus工具进行二次探索性因素分析、探索性结构方程建模(ESEM)和验证性分析,比较两种软件分析后的探索性因子结构和拟合指标;最终确定公因子数量,再根据模型简约化原则,对一阶因素进行二阶分析,得出能反映高阶思维要素关系的测量结构模型。
三、高阶思维结构因子分析过程与发现
由于高阶思维结构的复杂特征和测量难度,我们先利用SPSS探索性因素分析的成熟技术,初步确定公因子数目;再利用Mplus可以设定获得多个公因子模型结果及可以对拟合指数比较的特点,从拟合指标进行评价并最终确定最优公因子;最后利用Mplus因子探索与验证的双重功能,对探索出的最优公因子进行探索性结构方程建模(ESEM)和二阶测量模型建立。
1.SPSS探索性因素分析与公因子数目判断
(1)观测指标筛查
根據Kaiser(1970)的观点, KMO的值至少要在0.50以上,才可以进行因子分析,KMO值在0.9以上,极其适合进行因子分析。对高阶思维问卷数据进行KMO和Bartlett初始检验,得出样本的KMO(取样适当性)=0.961,Bartlett's(8256)=37149.197,p<0.001,表明量表适合于进行探索性因素分析。萃取特征值大于1的因子,共有20个公因子,总解释方差为67.159%。
高阶思维结构探索性因素初步分析结果显示:虽然观测变量总解释方差大于50%,但有一些观测变量的因子载荷较小(低于0.3),且一些公共因子仅有两个观测指标(每个公共因子不低于3个观测指标),可见初始得出的因子不属于稳定结构。因此,对于因素载荷低于0.3的观测变量逐条删除后再进行新的因素分析,直至所有观测指标的因子载荷均达到0.50以上(共删除61项题目)。删除后数据结果是:KMO(取样适当性)=0.969,达到“极佳”水平,表示变量间有公共因子存在;Bartlett球形检验的值为23345.202(自由度为1770),显著性概率值p=0.000<0.05,表示总体相关矩阵间有公共因子存在。因而KMO系数检验和Bartlett球形检验均表明变量适合进行因子分析。
(2)探索性因素萃取
因子萃取结果并不是唯一的,也不能说哪一种因子萃取的结果是绝对正确的,因子萃取是综合判断的一个过程。目前因子萃取主要依据特征值大于1、碎石图、公因子累积解释方差最低要求达到50%以上等原则。但每一种准则都有其内部局限性,因而一些研究者建议使用多种准则来确定模型中因子的萃取。考虑到本次研究的样本数量,我们参照Kaiser特征值大于1、碎石图检验法、方差百分比三种因子萃取原则。
根据特征值大于1的因子萃取原则,再综合考虑共同性、载荷系数、累积方差贡献率和一致性系数等指标,共产生三种因子萃取结果,见表1。其中,7个公因子和8个公因子共同性都在0.4以上;8个公因子和9个公因子的载荷系数都在0.5以上,均达到了理想的评价标准。综合考虑发现,8个公因子无论在数据上还是理论解释上相对其他两类都更为理想一些。
2.Mplus因素分析与拟合度评价
模型拟合度评价一般通过模型拟合指数判断。模型拟合指数通常分为三种:绝对拟合指数、相对拟合指数及信息指数,其中信息指数较少使用。不同类别的模型拟合指数可以从模型复杂性、样本大小、相对性与绝对性等方面对理论模型进行度量。Mplus提供的模型拟合指标及其评价标准见下表2(王孟成,2014)。
对三类公因子的探索性拟合指标结果比较(见表3),发现8个公因子模型的χ2/df、TLI、CFI和RMSEA几项指标最佳,9个公因子模型的AIC和SRMR两项指标最佳,7个公因子模型的BIC指标最佳。综合考虑各项模型拟合指标,8个公因子模型χ2/df、TLI、CFI与RMSEA等各项绝对和相对拟合指标都符合评价标准,信息指标AIC和BIC与其他两类公因子差异性较小。因此,8个公因子模型拟合指数是最好的。另外从Mplus探索性因素分析碎石图趋势分析来看,也是在8个公因子地方出现拐点(见图5)。
将Mplus与SPSS的8个因子探索性结果进行对比发现(表4),8个公因子包含的观测变量是相同的,不同的是Mplus分析的一些观测变量出现了跨因子现象,也就是一个观测变量可能对两个因子都有解释,这正是Mplus的特点之一,这也说明了高阶思维结构因素之间的相关性。
但是这8个公因子模型是否经得起验证性因子分析呢?我们利用验证性样本,分别将SPSS与Mplus萃取的8个公因子在Mplus中进行验证性因素分析,发现8个公因子的观测变量与以上两种工具分析的探索性因素观测指标是一样的,因子载荷差异性也不大,所得到的验证性拟合指标比较良好。但同时值得关注的是,验证性因子分析(CFA)中每个观测指标只能隶属于一个因子,而在其他因子上的负荷限定为零,这种限定往往会高估因子之间的相关以及与外部变量间的关系,从而影响研究的真实性。为此,我们又采用了探索性结构模型(ESEM)。
3.Mplus探索性结构模型
探索性结构方程建模(ESEM)是Muthen等人在2009年提出的新因子分析方法。这种方法整合了探索性因子分析( EFA) 和 CFA 两种因子分析方法的功能和优点,可以通过简单的设定获得多个公因子模型结果,并能对得到的多个公因子模型进行拟合指数比较,有效地克服了EFA 和 CFA 两种因子分析中存在的问题。目前这种方法已经在各类研究中得到广泛应用。由于高阶思维结构难以观测的复杂特征,本文将主要基于ESEM进行研究。这样既可以灵活地探索高阶思维的因子结构,又可以系统地验证其因子模型,为高阶思维结构潜变量之间的关系分析提供更适宜的测量模型。
将ESEM模型与CFA拟合结果发现,验证性模型的卡方自由度比、TLI和RMSEA几项指标均高于ESEM模型,这与CFA限制某些因子负荷为零会高估因子负荷、因子相关与外部变量的关系,从而使数值增高有很大的关系。为了更好地进行因素模型之间的比较,表5把Mplus的EFA拟合指标进行了整体比较,发现:EFA的TLI和RMSEA几项指标也均高于ESEM模型,ESEM的CFI、SRMR均高于EFA与CFA。可见,ESEM是比较理想的高阶思维结构测量模型。
将Mplus分析的探索性结构模型与验证性因素分析的因子载荷比较发现,8个公因子包含的观测变量是相同的。由于CFA限制因子负荷为零的原则,高估了因子之间的关系和载荷,所得出的因子载荷要高于ESEM的因子载荷。根据萃取因子载荷不低于0.3的原则,删除了Q21观测指标,这样最后保留了59个观测指标,因子载荷数值介于0.3~0.776,符合因子萃取的要求,见表6。
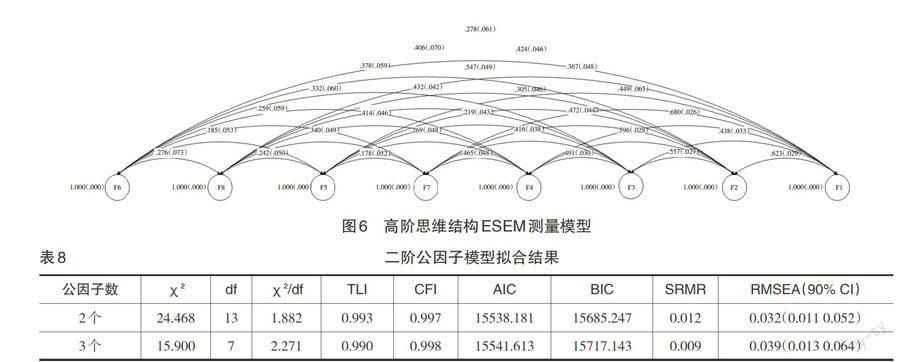
对各因子包含的观测指标内容进行整体分析:第一个因子包含17个观测指标,解释了学生如何运用新颖独特的方法进行学习,命名为创造性思维,符号为F1。第二个因子包含12个观测指标,解释了学生识别问题与解决的能力,命名为问题解决能力,符号为F2。第三个因子包含7个观测指标,解释了学习中同伴的相互帮助和支持,命名为同伴情感支持,符号为F3。第四个因子包含8个观测指标,解释了学生在学习中如果进行判断和选择,命名为推理与决策能力,符号为F4。第五个因子包含5个观测指标,解释了对他人观点的态度和行为合理性评价,命名为批判性思维,符号为F5。第六个因子包含4个观测指标,解释了学生在学习中如何进行计划和安排,命名为自我调节学习,符号为F6。第七个因子包含3个观测指标,解释了学生在元认知过程中的反思性评价,命名为元认知与反思性评价,符号为F7。第八个因子包含3个观测指标,解释了学生对于自己完成一个任务时的动机与自我评价,命名为自我效能感,符号为F8。具体高阶思维结构ESEM测量模型和因子命名分析说明如图6和表7所示。
4.二阶因子分析与测量模型建立
对相关系数矩阵与测量模型分析发现,因子之间相关系数高于0.7以上,说明因子之间存在高度的相关性和潜在的二阶因子,可以更抽象地概括与解释。因此,在一阶因子分析基础上,我们又进行了二阶测量模型分析,但二阶模型必须满足两个条件:一阶因子之间相关性较高,且二阶模型与一阶模型相比拟合度不能恶化,在理论上对能对一阶模型进行更高层次的解释和抽象概括。将已确定的一阶数据进行ESEM二阶因子提取,因子预设为2个、3个和4个。当提取4个公因子时,模型未被识别。以下为提取2个、3个二阶公因子模型拟合结果(表8)与因子载荷表(表9、表10)。
从模型拟合结果来看,提取2个公因子模型的卡方自由度比、TLI、CFI、AIC、BIC、RMSEA均优于提取3个公因子的模型,且提取3个公因子模型的RMSEA 90%置信区间的上限值为0.064,大于提取2个公因子模型的上限值。综合来看,提取2个公因子的模型拟合结果优于提取3个公因子的模型拟合结果。
从表9与表10分析,将F1-F8提取两个公因子时,公因子一包含F1、F4、F5、F7,公因子二包含F2、F3、F6、F7和F8,其中F7对公因子一和公因子二都有解释,即F7是跨荷因子,这也是ESEM在提取因子时候不同于其他因素分析工具的优势。将F1-F8提取三个公因子时,公因子一包含F5,公因子二包含F1、F4、F7,公因子三包含F2、F3、F6、F7和F8。其中F7同样对公因子一和公因子三都有解释。两种二阶公因子提取的因素载荷都不低于0.3,但提取3个公因子时有1个公因子观测指标只有F5,因此,提取2个公因子优于提取3个公因子。
为了更好地分析出高阶思维结构的二阶因子,我们根据思维结构的因素结构论、维度结构论、认知结构论、系统结构论、发展阶段论等文献分析,结合高阶思维本质、思维过程、思维策略及问题情境等因素,初步设定6种二阶高阶思维模型假设(见表11)。
其中模型1~2主要依照因素结构论设定,模型3~6主要从认知过程视角设定。模型1与模型2中的X1为认知因素,X2为非认知因素,X3为同伴情感支持,X4为元认知与反思性评价。模型1与模型2的最大区别是模型1把同伴情感支持、元认知与反思性评价作为单独的二阶因子,强调了同伴情感支持、元认知与反思性评价是高阶思维结构的重要要素。模型3~6中的X1为创造性策略,X2为问题解决过程;X3在模型4~6中指代不同,分别为批判性思维、批判性自我调节以及同伴情感支持;X4为元认知与反思性评价。模型3~6的主要区别是模型4把批判性思维作为独立的二阶因子,强调了批判性思维在高阶思维认知中的重要性;模型5把批判性思维与自我调节学习共同作为独立的二阶因子,强调自我调节学习在批判性思维中的重要性;模型6把同伴情感支持、元认知与反思性评价单独作为二阶因子,突出同伴情感支持、元认知与反思性评价在高阶思维认知中的重要性。对各模型验证拟合结果比较分析见表12。
对模型拟合指标分析发现:模型5和模型6的模型拟合结果较好,其次是模型3与模型4,模型1與模型2也满足了拟合指标要求。而且这6种拟合结果都没有恶化一阶模型拟合指标。结合二阶因素之间的相关性与理论分析,模型2与模型5无论从拟合指标还是理论分析都比较合理。模型2是从因素结构论把高阶思维结构一阶因素抽象概括为认知要素与非认知要素两个静态的二阶因素模型,模型5是从认知结构论把一阶因素解释成更抽象的创造性策略(X1)、问题解决过程(X2)与批判性调节学习(X3)三个动态的二阶因素模型。两种模型没有优劣区别,只是概述的角度不同,但也更加说明了高阶思维结构的复杂性与多样性。相对于因素结构论,我们更关注课堂情境中创造性策略、问题解决过程与批判性调节等高阶思维活动,这也与布鲁姆把分析、综合、创造作为高阶思维相契合,高阶思维的目标是培养创造性人才。因此本研究采用模型5作为高阶思维二阶测量模型。
5.高阶思维结构测量模型
通过综合运用SPSS与Mplus工具的优势与特点,我们通过探索性因素分析、探索性结构一阶测量模型与二阶测量模型的研究,最后得出在课堂情境中高阶思维8个一阶因子、3个二阶因子的测量模型结构,如图7所示。
图7中X1是创造性策略,包含创新性思维(F1)、决策能力(F4)、元认知与反思性评价(F7);X2是问题解决过程,包含问题解决能力(F2)、同伴情感支持(F3)、自我效能感(F8)、元认知与反思性评价(F7);X3是批判性调节学习,包含批判性思维(F5)、自我调节学习(F6)。在这个高阶思维结构三阶测量模型中,元认知与反思性评价(F7)作为跨荷因子贯穿在两个二阶结构中,说明元认知与反思性评价一直贯穿于整个高阶思维结构并对创造性策略与问题解决过程发生显著作用。从整个高阶思维二阶测量模型分析,高阶思维一阶因子之间、二阶因子之间、一阶与二阶因子之间都具有极高的相关性,证明了高阶思维是一个整体结构,各个因素不是独立存在的,高阶思维过程也是各个因素之间相互作用的过程。同时,高阶思维测量结构模型也说明了高阶思维是在课堂物质和文化环境中,在创造性思维、决策能力、批判性思维、元认知评价等认知因素,自我调节、自我效能感与同伴情感支持等非认知因素共同作用下,为了达到某种目的,识别问题、分析问题和解决问题所需要的高级综合能力。
四、讨论
结构是指物质系统内各组成要素之间的相互联系、相互作用方式,是人们用来表达世界存在状态和运动状态的专业术语。思维结构是思维活动特征的总和或整体。高阶思维结构作为人类大系统中一个开放系统,既有系统之间的复杂相互作用,又与外界环境保持着紧密的联系,因此高阶思维在本质上除了具有整体性、发展性等特征之外,还具有社会性、复杂性和难以测评性。各种与高阶思维能力相关的测量量表,比如,“托兰斯创造性思维测验”“加利福尼亚批判性思维倾向”“问题解决能力”等,虽然能对高阶思维某一个方面的倾向性或行为过程做出一定的评价,但缺乏对课堂教学情境中高阶思维发展过程及其能力的整体性评价和操作性指导,更忽略了对同伴情感支持、自我效能感和自我调节等非智力因素在高阶思维发展中的观测。
高阶思维的系统属性决定了高阶思维的行为不是一个孤立的领域,而是由认知、情感、动作的共同整合。高阶思维行为的习得、同化、适应和表现水平是由认知、情感和动作的相应类别和成分组成。也就是说,高阶思维学习过程都是完整的人的整体行为,智慧、情感和身体动作在学习过程中缺一不可,高阶思维发展目标的实现是以学习者外显行为统整认知、情感、动作的共同整合。因此,本文从课堂情境出发,基于高阶思维发展过程行为统整情感、动机的原理,采用因素分析法,通过对高阶思维结构进行ESEM探索,形成了以创造性策略、问题解决过程和批判性调节为核心的二阶高阶思维结构。在这个高阶思维结构中,不仅关注创造性思维、决策能力、批判性思维、元认知评价等思维技能与问题解决能力的行为特征,还关注自我调节、自我效能感、同伴情感支持等情感与动机的作用。反映在具体课堂情境中就是深层次学习、知识建构、问题解决等高级认知活动以及思维的自我监控等智力与非智力因素之间的相互作用。因此,本文基于行为统整形成的3个二阶因素和8个一阶因素的高阶思维结构模型对于全面认识高阶思维发展过程与活动的整体性具有重要的价值。但由于高阶思维的非线性、复杂性和難以观测性,我们对高阶思维结构的研究仅仅是从其外在表征——行为统整情感、动机等视角做了一些结构要素和动态特征的初步探索。在测量模型的基础上,下一步我们将对高阶思维结构各因素之间的相互影响及其因果结构效应进行更加深入地探索。这些系统化的研究将会为高阶思维课堂的教学培养与整体评价提供更加丰富的可操作范式。
参考文献:
[1][美]Dimiter M. Dimitrov(2015).心理与教育中高级研究方法与数据分析:从研究设计到SPSS[M].王爱民,韩涵,张若舟等.北京:中国轻工业出版社:126-128.
[2][美]Robert L. Linn, & Norman E. Gronlund (2003).教学中的测验与评价[M].北京:中国轻工业出版社:48-51.
[3][英]Rupert Wegerif(2009).思维、技术与学习综述(上)[J].魏晓玲,吉喆,钟洪蕊.远程教育杂志, (5):39-42.
[4]林崇德(2007).智力研究新进展与我的智力观[J].宁波大学学报(教育科学版),(5):1-7.
[5]麦玉娇,温忠麟(2013).探索性结构方程建模(ESEM):EFA和CFA的整合[J].心理科学进展,(5):934-939.
[6]盛群力(2008).旨在培养解决问题的高层次能力——马扎诺认知目标分类学详解[J].开放教育研究,(4):10-21.
[7]王孟成(2014).潜变量建模与Mplus应用[M].重庆:重庆大学出版社:67-71.
[8]王帅(2011).国外高阶思维及其教学方式[J].上海教育科研,(9):31-34.
[9]余林(2007).课堂教学评价[M].北京:人民教育出版社:142-145.
[10]钟志贤(2004).面向知识时代的教学设计框架——促进学习者发展[D].上海:华东师范大学:4-8.
[11]Kaiser, H. F. (1970).A Second Generation Little Jiffy[J]. Psychometrika,35(4):401-415.
收稿日期 2017-03-26 责任编辑 汪燕

