运用统计模拟法对人民币汇率中间价的趋势预测
摘 要:本文通过分析中国特色的汇率制度下人民币兑美元中间价汇率的历史运行趋势,运用间接方法探讨逆周期因子的影响计量模型,以评估对历史趋势的扰动性,进而对未来一段时期的人民币汇率中间价趋势进行初步预测。
关键词:汇率 统计模拟 趋势
中图分类号:F832.6 文献标识码:A 文章编号:2096-0298(2017)12(c)-045-02
1 研究的背景及目的
浮动汇率制分为自由浮动汇率制及有管理的浮动汇率制。目前我国尚不具备自由浮动汇率制度的条件,而采用有管理的浮动汇率制度。自2005年7月,中国人民银行宣布:我国开始实行以市场供求为基础、参考一篮子货币进行调节、有管理的浮动汇率制度。随着汇率市场化改革的持续推进,近年来人民币汇率中间价形成机制不断完善。2015年8月11日,完善了人民币兑美元汇率中间价形成机制,强调中间价报价要参考前一天收盘价。2015年12月11日发布人民币汇率指数,加大了参考一篮子货币的力度,以更好地保持人民币对一篮子货币汇率基本稳定。2016年2月份以来初步形成了“收盘汇率+一篮子货币汇率变化”的人民币兑美元汇率中间价形成机制,提高了汇率机制的规则性、透明度和市场化水平。2017年2月份将中间价对一篮子货币的参考时段由24小时调整为15小时,避免了美元日间变化在次日中间价中重复反映。
特别地,2017年6月,央行通知中间价报价银行于近期开始使用新的公式进行每日中间价报价。在之前的中间价计算公式中加入“逆周期因子”。该因子的引入,直接导致6月份人民币兑美元中间价出现了阶梯式跳跃。那么,在其影响下的人民币汇率的未来趋势如何呢?
2 研究的理论及方法
本文通过对2008年5月末至2017年5月末期间的人民币兑美元中间价(以下简称“中间价”)的时间序列资料进行分析,得出其资产漂移率及标准差。采用统计模拟方法(蒙特卡洛方法及基于Faure序列的拟蒙特卡洛方法),对2017年6月1日至2017年10月19日期间内的中间价进行趋势预测,通过与“逆周期因子”执行期间的实际汇率进行差异分析,拟合中间价历史汇率曲线,修正预测模型。进而对未来一定时期的中间价数值进行趋势预测。
2.1 资产价值漂移率μ及标准差σ的测算
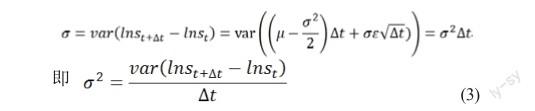
2.2 統计模拟方法
本文采用的统计模拟方法为蒙特卡洛模拟及拟蒙特卡洛模拟,二者的主要区别在于随机数发生器的发生机制。前者使用伪随机数序列进行模型模拟,后者主要用低差异性序列代替伪随机数序列进行模拟。
(1)蒙特卡洛模拟方法实际利用统计工具发生符合N(0,1)标准正态分布的伪随机数序列,通过高频的模拟次数模拟前述的变量。
(2)拟蒙特卡洛模拟方法通过发生低差异性序列,并经累计分布函数转化形成符合N(0,1)标准正态分布的高频序列模拟前述的变量。本文主要采用Faure序列发生器产生均匀分布序列,在通过Box-Muller方法将均匀分布序列转化为标准正态分布序列。本研究不再赘述Faure序列的发生原理[1]。另外,简单来说,Box-Muller方法是指通过如下变换过程将两组符合(0,1)上的均匀分布序列转换为两组标准正态分布序列[2]。
同理,模拟n次、每次97个数据点的汇率价格,得到n个1行97列方阵,合并为1个n×97方阵,对每列数据求均值,将该方阵“压缩”至1×97阶,当n=1000时绘制曲线如图2所示。
将这1000次模拟产生的最终1×97阶的数据方阵命名为MC。
3.2 拟蒙特卡洛模拟法
采用拟蒙特卡洛模拟法模拟上述期间97个交易日的汇率趋势步骤如下:
(1)使用faure序列发生器产生N个基底为b1的序列A。
(2)同上,使用faure序列发生器产生N个基底为b2的序列B。
(3)剔除A、B中的0元素数据,A、B各指针分别指向下一元素,得到A的子序列U1,B的子序列U2。则U1和U2均为符合(0,1)的均等分布序列。
(4)Box-Muller过程。根据公式(4)(5)将U1、U2变换为序列N1与序列N2,即N1与N2均为符合N(0,1)的标准正态分布序列。
(5)将各自均为1×N阶的序列N1和N2合并为2×N阶的N3,对每列求均值,“压缩”N3至1×N阶的N4序列。将N4按序均分为97个数据段,对每段数据求均值,用以分别模拟97个交易日的汇率价格。
因拟蒙特卡洛模拟法运用过程中产生的低差异性序列能够客服“维数灾难”,且在高频模拟次数下,生成的均等分布序列匀质性较好。另外考虑步骤(5)中数据分段的便利性,在实验过程中选择N=9700。
假设采用基底分别为2和3(也可采用其他基底,基底需为素数)的faure序列来进行模拟,绘图如图3所示。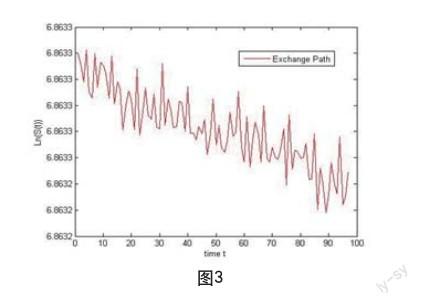
综上,表1中对比了蒙特卡洛模拟方法MC生成的数据序列、拟蒙特卡洛模拟方法QMC生成的数据序列及真实值Real Value的描述统计信息。
3.3 “逆周期因子”的影响计量
由于央行暂未公布“逆周期因子”的计算方法以及比重,在此简单假设如下模型: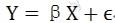
其中,Y为中间价汇率的真实值,X为拟蒙特卡洛模拟法生成的数据序列,采用OLS回归分析得到分析结果如表2所示。

3.4 人民币中间价的预测模拟
采用拟蒙特卡洛模拟方法,以2017年10月20日始至2018年6月30日止,模拟未来第174个中间价报价日(工作日)的中间价,带入式(7)进行数据修正,以考虑“逆周期因子”的影响扰动,最终得到中间价数据约为6.3381。
4 结语
本文的研究表明拟蒙特卡洛模拟法相较于蒙特卡洛模拟法发生的随机数更为稳定、匀质。在对汇率的趋势性预测中起到了较好的模拟效果。另外对于“逆周期因子”的影响作用采用了较为保守的OLS拟合方法,为人民币汇率中间价的预测建立了可参考的理想化模型。然而,对于具体“逆周期因子”数值的量化求解并未给出答案,仍需将来的后续研究。另外,本研究基于了多种理想性假设,例如假设汇率变动符合几何布朗运动及其维纳过程、汇率历史的波动性分析中并未考虑中国汇率制度政策的几度改革影响、未来汇率趋势预测中无法预知未来汇改政策的或有。因此对于我国有管理的浮动汇率制度的研究仍将是一个长期性、可研性的探索过程。
参考文献
[1] 黄仿伦.Faure序列的一种构造方法[J].安徽大学学报自然科学版,2004,28(3).
[2] 李玄锡.金融工程数值分析基础[M].经文社,2007.
[3] 王建.Quasi-Monte Carlo (ELW)[D].(Quasi-Monte Carlo模拟法对韩国股指渦轮的评价.仁荷大学,2012.
[4] Black,F.and M.Scholes.The Pricing of Options and Corporate Liabilities[J].Journal of Political Economy,1973,81(3).
[5] BrandimarteP.Numerical Methods in Finance and Economics[M].Wiley-Interscience,2006.

