基于SLM工艺的航空支架优化设计

（北京工业大学激光工程研究院，北京 100124）

SLM（激光选区熔化）是一种使用激光熔化金属粉末，逐层成形的增材制造工艺，相比传统工艺，其主要优势为：可以成形内部复杂结构；一体成形，保证整体强度；不需要任何工具辅助成形；可以成形变截面结构以优化结构强度。

SLM由于不使用任何切削工具进行成形，因此针对SLM的结构设计不受传统工艺的约束，但为了追求效率，降低成本和成形风险等目的，需要遵循一定的设计规则。

成形方位（包括零件距基板高度、特征面与成形方向角度等）决定了支撑区域、支撑用量、成形风险及精度和结构性能等。Strano等[1]通过算法确定零件成形所需的最少支撑量，从而来增加后处理效率。Snyder等[2]则对成形方向对微流道的成形误差和精度进行了研究。

支撑在SLM工艺中与零件同时成形，其主要作用是将零件固定在基板上，同时由于工艺过程中存在热应力产生的变形[3-4]，可起到防止几何形变[5]的作用，此外还能够防止熔池塌陷[6]，保证成形过程的稳定性。在零件打印前对其位置摆放进行优化[7]，有可能减少支撑的使用，从而减少材料的使用和制造时间及后续去支撑时间。在使用支撑时，其支撑面会因支撑的存在而表面质量变差[8]，因此应尽量减少支撑的使用。

现阶段，由SLM成形的大多数结构是由传统工艺条件下的参数化建模方法构造的，由于不以SLM工艺性为前提进行设计，常会出现成形稳定性差，支撑密度大且难去除，最佳成形方位无法匹配零件质量等问题。本文通过对已有轻量化结构进行结构和工艺性分析，利用拓扑优化[9]和形状优化等手段，结合SLM工艺特征在保证原始性能的条件下进行重新设计，研究原始模型的轻量化设计潜力和优化结构SLM工艺性，并通过结果对比验证优化结构的可行性。

1 优化设计的SLM工艺性原则

在保证成形质量上，为防止表面球状效应和抑制翘曲变形，悬垂面需要支撑结构进行辅助。图1展示了对悬垂面添加支撑的成形结果。可以看到，支撑使表面成形质量恶化，且与厚度较小的薄壁结构融合，增加了后处理难度。因此，自支撑结构设计是SLM设计追求的目标。

在本文中，最大角度为45°。图2展示了如何通过优化设计，去除支撑实现结构的自支撑。除了通过改变形状减少支撑的使用量外，还可以通过采用镂空结构减少支撑使用量甚至是实现自支撑。

图1 不同厚度成形Fig.1 Molding of different thickness

图2 优化设计Fig.2 Optimized design

图3 刮刀与零件作用示意图Fig.3 Illustrations of interactions between blade and part

在成形稳定性方面，SLM相关设计指导手册中对提高可制造性的结构与工艺设计提出了指导性建议。图3中为理想状态下刮刀与零件作用方式示意图。由于刮刀在运动过程中与已成形层接触，在刮刀运动方向上会产生牵引力，对成形过程造成影响。理想状态下的成形截面为圆形轮廓，见图3（a）。圆形轮廓在与刮刀接触时为点接触，可以使刮刀平滑掠过已成形层，同时圆形轮廓具有几何稳定性，可以抵抗刮刀在成形层上运动时产生的牵引力。图3（b）的U型轮廓也具有圆形轮廓的特点，但要注意其摆放方向的要求以抵抗刮刀牵引力。

此外，其他对成形稳定性有影响，且应尽力避免的状况为：块状的几何结构不能与基板大面积接触，也不能产生大面积的分层截面，引起表面变形，甚至使成形结构与基板分离；尖锐边、角在成形过程中会造成结构翘曲，与刮刀碰撞，终止成形过程；在分层面积突变处，会积累大量应力，导致结构断裂。

2 优化设计原理

优化设计的通用数学模型为：

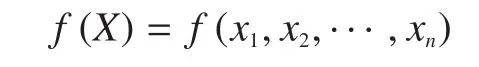
约束条件为：

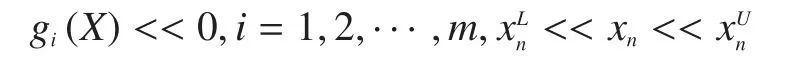
式中，X=x1，x2，…，xn为设计变量；f（X）是目标函数；gi（X）是不等式约束函数。本文的材料模型使用SIMP方法，即变密度法。单元密度被归一化与单元刚性矩阵直接关联，即为惩罚系数为惩罚后单元刚性矩阵，K为实际材料刚性矩阵。在OptiStruct中，设计变量即为归一化密度ρ，其上限和下限分别为0和1。

本文采用最小化数学模型，即优化目标为体积最小化，约束为加权柔度，数学模型为：

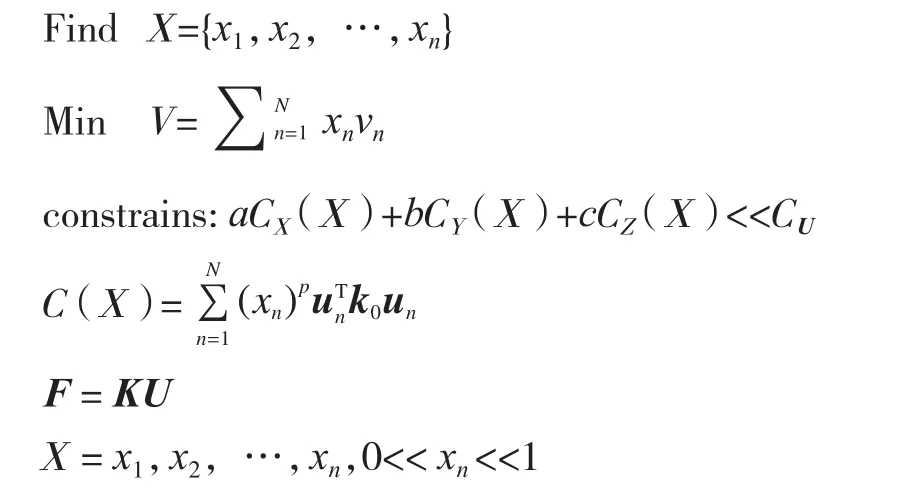
式中，V为结构体积；xn为单元设计变量；vn为单元体积；un为单元n的位移向量；k0为单元初始刚度矩阵；F为结构整体载荷矩阵；K为结构整体刚度矩阵；U为结构整体位移矩阵； CX（X）、CY（X）、CZ（X）分别为各工况下柔度函数；a、b、c分别为加权系数。

3 原始设计结构分析与SLM工艺性分析

图4（a）为原始支架设计，原始结构符合传统切削工艺的设计原则，通过加强板对结构进行横向位移约束，并在侧壁及加强板上均有大小不同的开孔，以最大程度去除材料，达到轻量化的目的。原始结构最薄处为5mm，最厚处为8mm，材料采用铝合金，体积系数为1.64，整体最大长度为470mm。

通过有限元分析进行工况模拟，得到原始设计的工况下最大位移为0.339mm，一阶和二阶特征频率为342Hz和383Hz，最大位移分别为0.046mm和0.035mm。

由于要保证安装面的表面质量，因此安装面应尽量采用自支撑结构，通过优化安装方位，比例因子为0.5的零件摆放位置见图4（b），红色为支撑结构，可以看到安装面上有大量块状支撑与基板连接，由于加强板的存在，大量块状支撑与结构内部接触，部分支撑通过安装面与基板连接，而过高的支撑结构增加了材料用量的同时也增加了成形风险。原始模型大量的内部支撑会增加后处理难度，因此在进行设计时应尽量避免形成内部支撑结构。

4 优化设计与工艺性分析

优化设计要求为在保证刚度的条件下最大程度减轻重量，缓解应力集中，抑制结构变形，同时提高特征频率。重新设计根据SLM设计原则进行，使用复杂曲面建模，以获得圆滑分层截面，同时采用分立结构以防止出现材料块状积累，原截面突变处采用圆角以使截面积平滑过渡。结构优化的目标函数为体积最小，约束条件为柔度最小。整个过程使用OptiStruct[10-11]软件的变密度优化法进行原型设计，材料类型为铝合金，之后对原型设计使用自由型优化进行迭代设计。

有限元模型及工况如图5所示。红色三角表示模拟螺栓固定，箭头表示安装面所受各向质量块在加速度条件下的载荷，同时整个结构受Y向10倍重力加速度。红色箭头表示在X方向安装面施加载荷等效静力1000N，绿色和蓝色箭头分别表示Y向和Z向被施加载荷等效静力1000N。网格绿色部分为非设计域，蓝色部分为设计域。

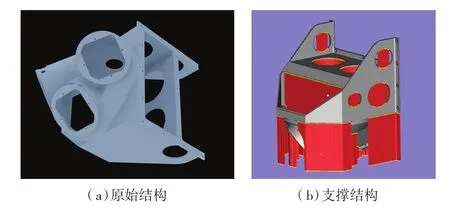
图4 原始支架设计Fig.4 Original support design

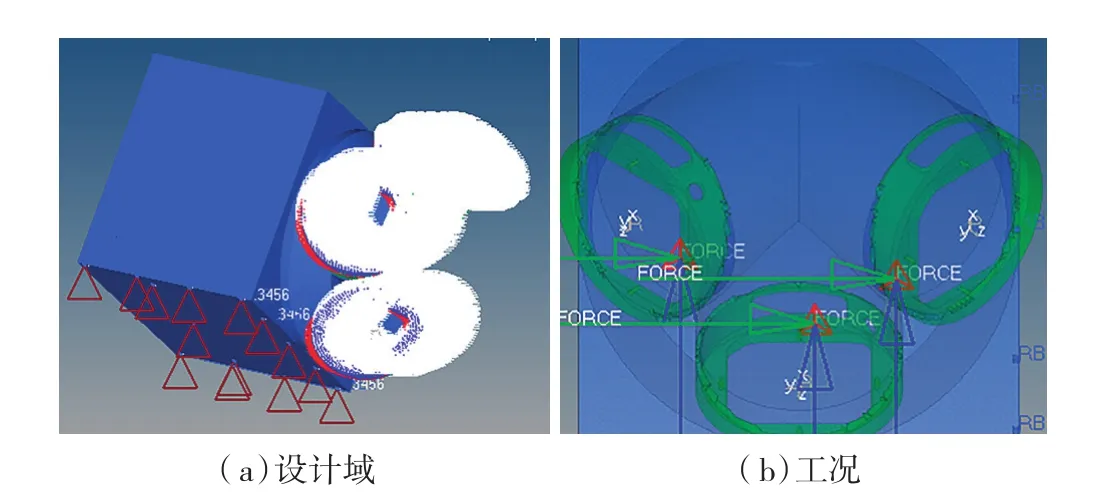
图5 设计域与工况Fig.5 Design domain and working conditions

图6 优化结果与最终设计结果Fig.6 Optimization result and final design result

拓扑优化结果如图6（a）所示，最终设计如图6（b）所示。优化设计以拓扑优化结果作为参考，并以SLM工艺性为指导，对整个零件进行分体设计，安装头使用镂空设计，螺栓连接支架使用复杂曲面设计以尽量优化支撑使用。图6（b）为轻量化结构，其由大量不规则复杂曲面构成，并且存在非对称镂空结构和开孔，整体结构尽可能满足自支撑形成条件。结构质心由原先的（1.807，2.211，-0.326）移动到（-3.506，2.876，-3.006），移动距离为6mm，与原设计相差不大。

图7为比例因子0.5优化结构的SLM成形工艺图，由于优化设计考虑减少支撑使用量的要求，取消了加强板，降低了支撑使用量和成形风险。整体刚性由变截面结构与三角形构造进行补偿，同时由于变截面设计的存在，进一步降低支撑使用量。安装面上部由爪状结构组成，为避免形成过高的支撑，同一侧的爪状分支基本处于同一平面，支撑结构上下两端与爪状分支相连接。

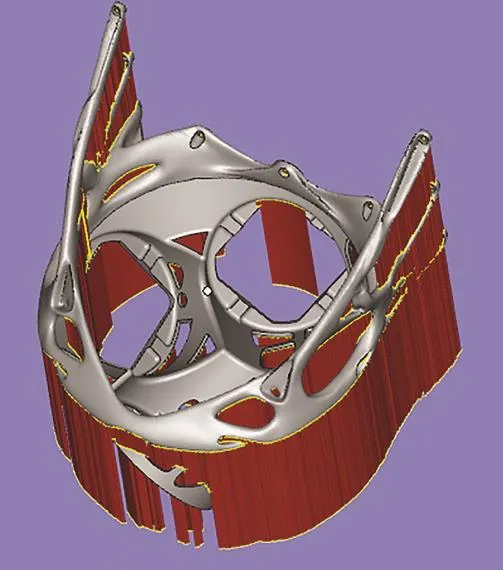
图7 优化设计工艺图Fig.7 Optimized design process diagram

安装面部分使用镂空设计以减少重量，同时减少安装面在基板上的投影面积，以进一步减少支撑使用量。

5 结果与讨论

通过对比图8和图9各等效工况位移图，优化后X轴工况分析结果显示，其安装头变形方向与原设计基本一致，位移量也相同，Y轴位移小于原设计。优化后Z轴工况结果显示，在工件位移红色部分采用了三角形构造，并增强了三角形构造与主构造的连接强度，成功抑制了Z轴位移，位移量减少了32.7%。

图8 原设计位移云图（受力方向从左至右为：X、Y、Z）Fig.8 Original design displacement cloud (load direction from left to right: X、Y、Z)

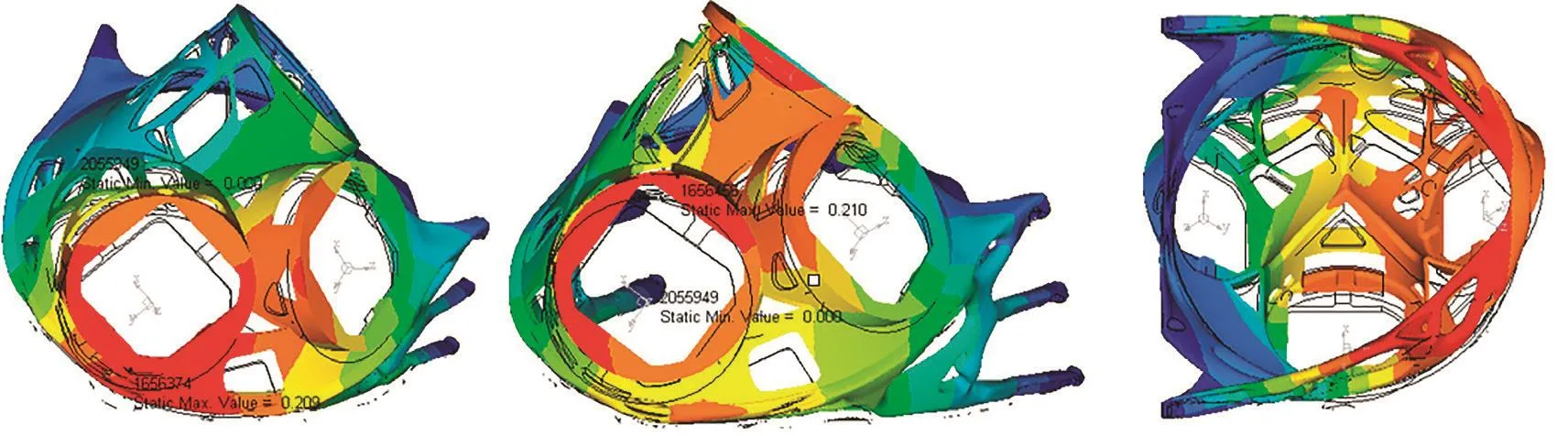
图9 优化设计位移云图（受力方向从左至右：X、Y、Z）Fig.9 Optimal design displacement cloud (load direction from left to right: X、Y、Z)

图10 原设计应力云图（受力方向从左至右为：X、Y、Z）Fig.10 Original design stress cloud (load direction from left to right: X、Y、Z)

图11 优化设计应力云图（受力方向从左至右：X、Y、Z）Fig.11 Optimal design stress cloud (load direction from left to right: X、Y、Z)

通过对比图10和图11各等效工况应力图，优化后X轴工况应力分析结果显示，应力更多集中于螺栓固定处的爪状结构上，以此限制了爪状结构的位移。优化后Y轴工况分析结果显示，镂空区域将原本集中的应力分布转为分散在整个结构中，同时螺栓连接承受更大应力以固定零件，其他区域应力情况基本与X轴工况下相同。优化后Z轴工况结果显示，整个应力分布与原设计基本相同，但由于镂空结构，应力在螺栓连接处的应力分布比较集中，最大应力出现在螺栓连接处。从表1中可以看到，优化结构整体性能有较大提升，除X轴工况性能与原设计性能接近外，其他工况都有较大改善，基本实现了性能要求。表1为优化结构分析数值与对比（括号内数值）。

图12和图13分别为不同高度时优化结构与原结构的分层截面形状图，可以看到优化设计的分层截面形状相比原设计没有大面积的材料连接区，其截面基本由不规则圆弧构成，确保在任何成形方向，结构与刮刀都是点接触。说明设计结构较原设计更适合使用SLM成形。

表2为在同样的工艺参数下成形所需材料和时间的估计值。最终结果显示，优化设计较原设计材料用量减少65.6%，成形时间缩短38.6%，尤其是其支撑用量减少74.8%，验证了优化设计的去支撑效果，降低了后处理难度。表2为比例系数0.5条件下的结果。

6 结论

（1）优化结构使用变截面及镂空设计，各工况位移最大减少32.7%，刚性提高38.3%，减重24.3%。结构长度减小90mm，宽度增加30mm，应力集中得到缓解，框架体积减少12.2%，提高了空间利用率。

（2）由于优化结构根据SLM工艺设计原则进行设计，在比例因子为0.5的条件下，支撑体积大幅减少74.8%，在同样摆放位置状态下，优化结构材料用量减少65.6%，成形时间缩短38.6%。由于在结构内部没有支撑存在，优化设计也降低了后处理难度。

（3）设计结果表明，对于薄壁支架零件，采用拓扑优化和3D打印相结合的方式进行制造能够得到更轻、性能更好的结构。

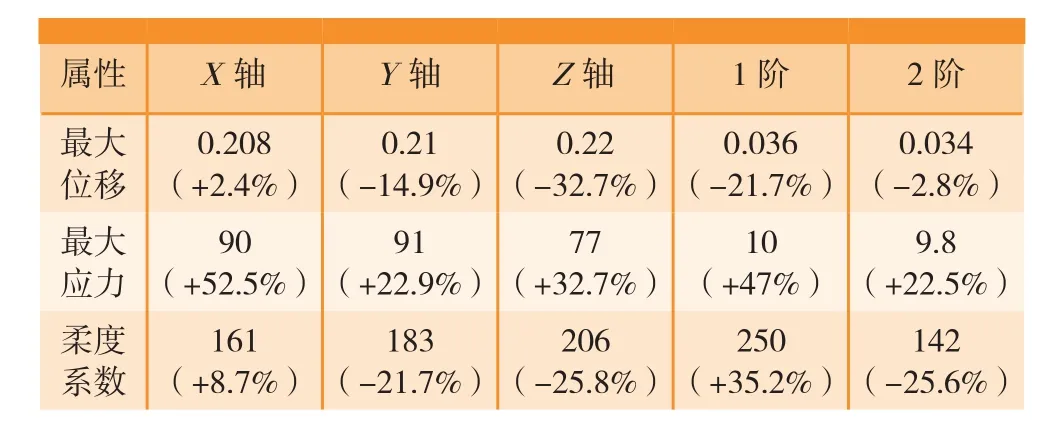
表1 轻量化设计分析结果

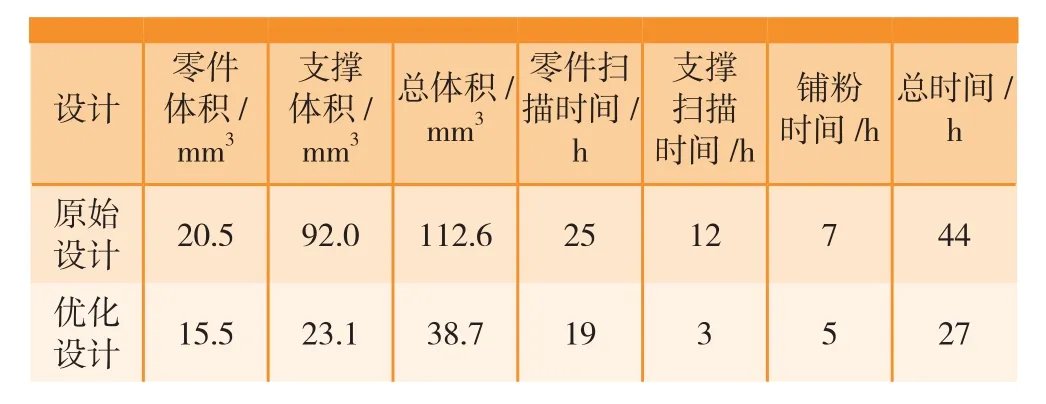
表2 SLM工艺指标

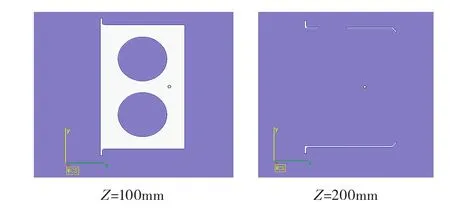
图12 原结构截面形状图Fig.12 Cross-sections of the original design

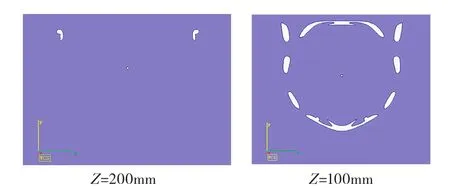
图13 优化结构截面形状图Fig.13 Cross-sections of the optimal design

[1]STRANO G, HAO L, EVERSON R M, et al. A new approach to the design and optimisation of support structures in additive manufacturing[J]. The International Journal of Advanced Manufacturing Technology, 2013, 66(9-12): 1247-1254.

[2]SNYDER J C, STIMPSON C K, THOLE K A, et al. Build direction effects on microchannel tolerance and surface roughness[J].Journal of Mechanical Design, 2015, 137(11): 111-114.

[3]KRUTH J P, LEVY G, KLOCKE F, et al. Consolidation phenomena in laser and powder-bed based layered manufacturing[J].Annals of the CIRP, 2007, 56(2): 730-759.

[4]张凯，刘婷婷，张长东，等. 基于熔池数据分析的激光选区熔化成形件翘曲变形行为研究[J]. 中国激光, 2015(9): 135-141.

ZHANG Kai, LIU Tingting, ZHANG Changdong, et al. Study on deformation behavior in selective laser melting based on the analysis of the melt pool data[J]. Chinese Journal of Lasers, 2015(9): 135-141.

[5]CALIGNANO F. Design optimization of supports for overhanging structures in aluminum and titanium alloys by selective laser melting[J].Materials & Design, 2014, 64: 203-213.

[6]曹冉冉，李强，钱波. SLM快速成形中的支撑结构设计研究[J]. 机械研究与应用, 2015(3): 69-71, 76.

CAO Ranran, LI Qiang, QIAN Bo. Design of support structure in SLM rapid prototyping[J]. Mechanical Research & Application, 2015(3): 69-71,76.

[7]ALLEN S, DUTTA D. On the computation of part orientation using support structures in layered manufacturing[R]. Austin: Solid Freeform Fabrication Symposium, 1994.

[8]THOMAS D. The development of design rules for selective laser melting[D]. London: University of Wales Institute, 2009.

[9]顾卫平, 刘小涛,李刚. OptiStruct结构优化技术在航空产品设计中的应用[C]// 中国的设计与创新学术会议. 上海, 2011.

GU Weiping, LIU Xiaotao, LI Gang. Application of structure optimization technology optiStruct designing of the aviation product[C]//Academic Conference on Design and Innovation in China. Shanghai, 2011.

[10]ESCHENAUER H A, OLHOFF N. Topology optimization of continuum structures: A review[J]. Applied Mechanics Reviews, 2001,54(4): 1453-1457.

[11]苏胜伟. 基于OptiStruct拓扑优化的应用研究[D]. 哈尔滨:哈尔滨工程大学, 2008.

SU Shengwei. Application and research of topology optimization with optiStruct[D]. Harbin: Harbin Engineering University, 2008.