基于Markov链的最优进货策略研究

李 超，商玉萍(安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

基于Markov链的最优进货策略研究

李 超，商玉萍
(安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

为了构建最优的进货策略以维持市场份额，降低库存带来的成本和损失，基于某商店的市场销售数据，使用频数直方图、函数回归拟合、差分方程、转移概率矩阵等方法，得到零售品的销售规律为泊松分布，并结合市场需求量的概率分布函数对每一商品的库存量进行Markov状态预测，得到关于进货策略问题的市场需求、最佳进货量、平均缺货时间和缺货量等结果，提出了一种基于规避成本和损失的最优进货策略．

进货策略；库存；泊松分布；Markov链

对于一个商店而言，其经营目标能否实现，经营业绩能否完成，关键在于商品结构是否合理，如果商品结构不合理就会直接影响商店的经营成果，这个时候进货就显得非常重要[1]．商店的进货策略，应当遵循谨慎性原则的要求，采取全局统筹的做法，合理核算可能发生的损失和费用．以商店的经营成本来考虑商店的盈利，即商店的经营成本最小时其盈利就最大，此时的进货方案即为最佳进货方案．在不允许缺货的情况下，商店的经营成本为进货费用与商品储存费用之和；考虑到允许缺货的情况，商店的经营成本为进货费用、商品储存费用与缺货损失费用之和．所以，为了降低商店的经营成本，就需要实行库存控制．库存控制要考虑几个方面：销售量、到货日期、采购周期以及市场需求量．以往研究都是以库存环境不变为前提，而忽视了商品需求的动态变化过程，缺乏了实际可操作性．

根据市场分布情况得到商品的需求量为泊松分布形式，然后采取无后效性的马尔科夫概率转换矩阵，计算出缺货时间及缺货量，进而得到了商店进货周期和库存的最佳进货机制，以期对零售业的降本增效、提升经营效率给予启示．本文有假设：(1) 货源供给能力无限大，进货是瞬间完成的；(2) 该商店的商品销售并没有采取广告宣传和其他刺激消费的措施；(3) 商店储存能力固定．

1 数据准备

数据采用某个商店的实际销售数据，并将市场需求分为每日需求和长期需求，从这2方面考虑．由于商店的3种商品的销售量一直比较稳定，可以用销售量确定日需求量和长期市场需求量．

1.1 基于销售量分布的日需求量分析

第1步：由A、B、C 3种商品的销售量的频数[2](如表1所示)，绘制3种商品的频数直方图(如图1所示)．第2步：结合频数分布直方图，假定商品A、B、C的销售量符合泊松分布，选择泊松分布对销售量进行函数拟合，效果极佳(见图2)，则得到商品A、B、C需求量的分布函数：

表1 商品A、B、C的销售量频数表

图1 商品A、B、C的频数直方图(曲线代表商品A、B、C的频数折线图)

图2 商品A、B、C需求量的分布函数拟合图

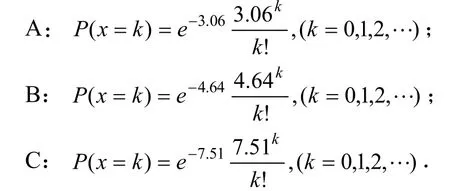
则可知A、B、C 3种商品的平均每日市场需求量：

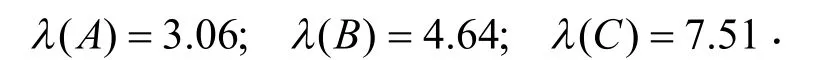
1.2 长期趋势条件下的市场需求量情况预测

对A、B、C 3种商品前k天的销售总量进行一元函数线性拟合，做出销售总量与天数的关系图，见图3．由此可得A、B、C 3种商品的长期市场需求模型

图3 商品A、B、C销售总量与天数的关系图

2 既定分布条件下Markov转移模型

2.1 问题的分析

商品的日储存量属于随机状态，仅于前一天贮藏量有关且该状态无后效性，即日储存量的变化过程可用Markov链描述[3]．

对于商店的存贮情况，商品存贮量变化的差分方程模型：

由 Markov链描述每日库存量的过程，即该商店第二天的库存量仅取决于当天的库存量和转移概率．

通过每日库存量的转移概率an，an满足可求该店三类产品的缺货时间与缺货量，即在已知日需求量的概率分布的情况下，当需求超过库存时就会失去销售机会，可以计算这种情况发生的概率．在动态过程中这个概率每天是不同的，每周的销售也是不同的，可以考虑让时间充分长之后按稳态情况进行分析和计算，缺货量则可以用期望的方式求出[4]．

2.2 Markov链模型的建立

由于状态转移矩阵P中所有的值均大于0，即矩阵正，则存在唯一极限状态概率向量使得当状态概率即为稳态概率，满足

由此得出商品A每日的稳态概率，同理可以求到商品B、C每日的稳态概率(商品C的稳态概率表较大，未附上)，见表2、表3．

表2 商品A的稳态概率

表3 商品B稳态概率

2.3 基于Markov链求解缺货概率

商品X第n天的日需求量超过第n天末的库存量Dn的概率，即缺货的概率：

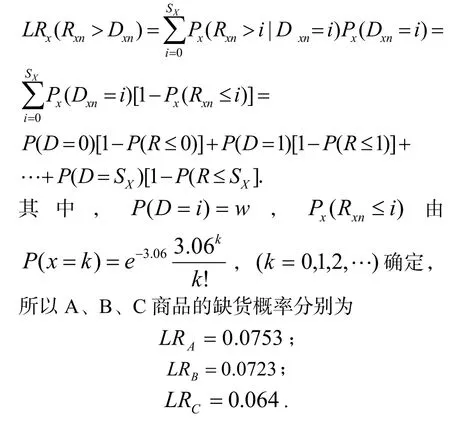
2.4 最优进货策略

同理可以求到B、C商品的缺货时间以及缺货量．

结果整理见表4．

表4 商品A、B、C的缺货时间，缺货量

在商店的一定经营周期内，根据缺货时间和缺货量，可以得到商店每种商品的进货周期和进货量．A商品的进货周期为62 d，进货量为151件；B商品的进货周期为60 d，进货量为215件；C商品的进货周期为53 d，进货量为259件．

3 结语

对于零售企业而言，准确的把握住市场、合理规避库存成本是生存的关键，但是在纷繁复杂的市场环境和变动的成本因素下，怎么才能确定合适的进货策略显得非常重要．本文在合理的假设条件下，提出一种基于马尔科夫链的状态转移模型对解决这个问题具有很强的启示意义．未来的研究可以尝试引进每件单品的利润、运输费用、存储费用等，从而对模型进行进一步的完善．

[1]李颖丽. 一种基于条件分布Markov状态转移的零售库存策略[J]. 统计与决策, 2012, 367(19): 180-182.

[2]吴礼斌. 经济数学实验与建模[M]. 天津: 天津大学出版社, 2009.

[3]姜启源, 谢金星, 叶俊. 数学模型[M]. 北京: 高等教育出版社, 2003.

[4]张清忠. DRP系统决策支持模块的算法设计[J]. 湖南城市学院学报: 自然科学版, 2016, 25(4): 132-133.

(责任编校：陈健琼)

Optimal Purchase Strategy Based on the Markov Chain

LI Chao,SHANG Yu-ping
(School of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu, Anhui 233030, China)

In order to build the optimal purchasing strategy to maintain market share, reduce the cost and loss of inventory, the methods of frequency histogram, function regression, difference equation and transfer probability matrix are used based on the market sales data of a certain store, the law of retail sale is Poisson distribution. Then Markov state inventory is predicted with the probability distribution function of the market demand for each commodity. Finally, the purchase strategy of market demand, the optimal order quantity, the average time shortage and shortage are get, an optimal purchase strategy is proposed based on the cost and loss.

purchase strategy; inventory; Poisson distribution; Markov chain

O227

A

10.3969/j.issn.1672-7304.2017.01.10

1672–7304(2017)01–0045–04

2016-12-01

国家社会科学基金项目(11CTJ006)；安徽财经大学研究生科研创新基金项目(ACYC2015090)

李超(1980-)，男，副教授，博士，主要从事宏观经济统计、综合评价方法与应用研究．E-mail: 1767530753@qq.com