基于加速度约束等残留高度刀轨生成算法

梁奉兴，董 峰，徐汝锋，刘纪凯

(山东理工大学 机械工程学院，山东 淄博 255000)

基于加速度约束等残留高度刀轨生成算法

梁奉兴，董 峰，徐汝锋，刘纪凯

(山东理工大学 机械工程学院，山东 淄博 255000)

针对传统的等残留高度刀轨规划算法加工自由曲面时刀轨不光顺问题，提出了一种基于加速度约束等残留高度刀轨生成算法。通过判断同一条刀轨相邻刀触点之间的平均加速度来调整不符合加速度条件的刀触点，从而保证刀具轨迹的光顺性。基于该算法利用VC++6.0和UG OPEN/API二次开发平台编写程序。对拟合自由曲面得到的参数曲面进行处理后，并在UG(Unigraphics NX)CAM模块进行刀路模拟。结果表明，该算法有效的改善了刀具轨迹的光顺性，得到了理想的效果。

加速度约束；等残留高度；刀具轨迹；UG OPEN/API二次开发

0 引言

目前数控加工刀具轨迹规划方法：主要有等参数线法、截面线法、导动面法、投影法和等残留高度法等[1-3]。前两种方法应用广泛且较为简单，但当曲面曲率变化较大时，刀具路径参数选择较为保守，影响加工效率。等残留高度法较前几种方法可以产生最优刀具路径，生成的总刀轨长度最短，但后续刀具轨迹变形严重成了该算法最大的缺点。赵世田[4]提出了一种基于等残余高度线的加工步距最大化算法，提高了残余高度计算精度和曲面的加工质量。李占君[5]等通过控制刀具轨迹线的曲率来保证刀具轨迹光顺性，这在某种程度上使刀轨光顺，但是轨迹线的局部会产生波浪形。李铁军[6]等引入参数行距方向摆动修正值来修正轨迹线上出现的折线。本文针对传统等残留高度算法的缺点提出了一种基于加速度约束等残留高度光顺刀轨生成算法。对同一条刀轨上相邻三个刀触点之间进行平均加速度判断，若不符合加速度约束条件，则重新搜索刀触点，保证刀具轨迹的光顺性，从而提高刀具运动的平稳性，提高加工质量，避免刀具急剧磨损。

1 刀轨生成的理论基础

1.1 测地线的曲率半径及方向计算

设自由曲面的参数方程为S(u,v)，假设一条刀具轨迹线为r(u(t),v(t))。P0为曲线上的一个刀触点，dr为该点走刀方向向量，n为曲面在该点处的法向量。dr*为该点测地线方向向量，Rn为该点的法曲率半径。P*由相邻轨迹上等残留点P0求得，如图1所示。

图1 相邻轨迹点的计算

由微分几何知识[7]得到，曲面的第一基本公式和第二基本公式为：

(1)

(2)

式中：E、F、G—曲面的第一类基本量，L、M、N—曲面的第二类基本量。

曲率半径：

(3)

已知参数曲面上经过一点的任意一条曲线的切向量在以(du，dv)构成的切平面内，并且该切向量方向可由du:dv确定。曲面上在点S(u,v)的任意切向量可表示为：

dr=rudu+rvdv

(4)

ru，rv—分别为曲面在点S(u,v)处对u参数和v参数的偏导数。

由测地线性质[7]得dr垂直于dr*：

(Sudu+Svdv)(Sudu*+Svdv*)=0

(5)

式中：(du*，dv*)—测地线方向。

于是得到du*和dv*之间的关系：

(6)

把(6)式代入(3)式得到测地线的曲率半径为：

(7)

1.2 相邻等残留轨迹点的计算

选取最长的一条边界u0或v0作为第一条轨迹，采用等参数离散逼近的方法确定加工步长[8]，把同一条轨迹相邻两点连线方向作为走刀方向。每一个刀触点处的参数增量[6]为：

(8)

L-行距[6]，由加工误差、刀具有效半径和测地线方向曲率半径求得。式中正负号需要根据加工方向来确定。

因此已知某轨迹线上一刀触点，就可求出相邻轨迹对应的刀触点：

P*(t)=P0(u(t)+Δu,v(t)+Δv)

(9)

2 刀触点的调整和确定

由上一节得到一行刀轨上所有刀触点后，计算每相邻三个刀触点之间平均加速度，进而对每个刀触点(舍去前两个刀触点)进行判断并调整。

2.1 平均加速度的计算

假设已知一条刀具轨迹线为Cj(u(t),v(t))，已知刀触点Pi，Pi+1，Pi+2，Pi+3，Pi+4，Pi+5。依次求出相邻三个刀触点之间的平均加速度，如Pi到Pi+2路段的平均加速度ai，Pi+1到Pi+3路段的平均加速度ai+1，Pi+2到Pi+4路段的平均加速度ai+2等，如图 2所示。

图2 同一轨迹上相邻刀触点之间平均加速度的计算

2.2 依次刀触点处平均加速度的判断和调整

默认接受每条轨迹的前两个刀触点，利用加速度约束依次判断刀触点的流程图，如图3所示。

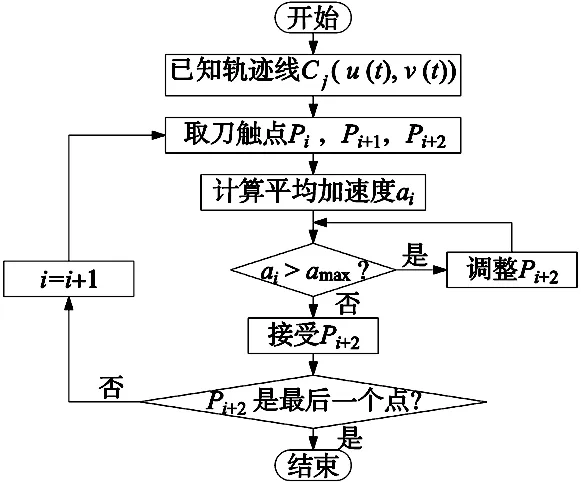
图3 同一条刀轨上刀触点的判断过程

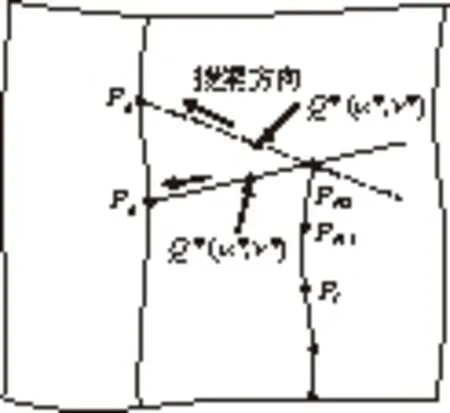
图4 刀触点Pi+2的搜索示意图

图4是调整Pi+2时的搜索示意图，其中Pi+2是由P0求得。在u，v参数增量方向按照Δu、Δv的比例进行搜索，设定一个搜索参数l(取正整数，如可设为10)来控制搜索步长，u，v参数增量方向搜索步长分别为Δu/l、Δv/l。当参数增量Δu<0时在虚线上搜索，即红色内容，否则在实线上搜索。其实搜索公式相同，因为Δu前面的符号会抵消掉。调整Pi+2的流程图，如图5所示。

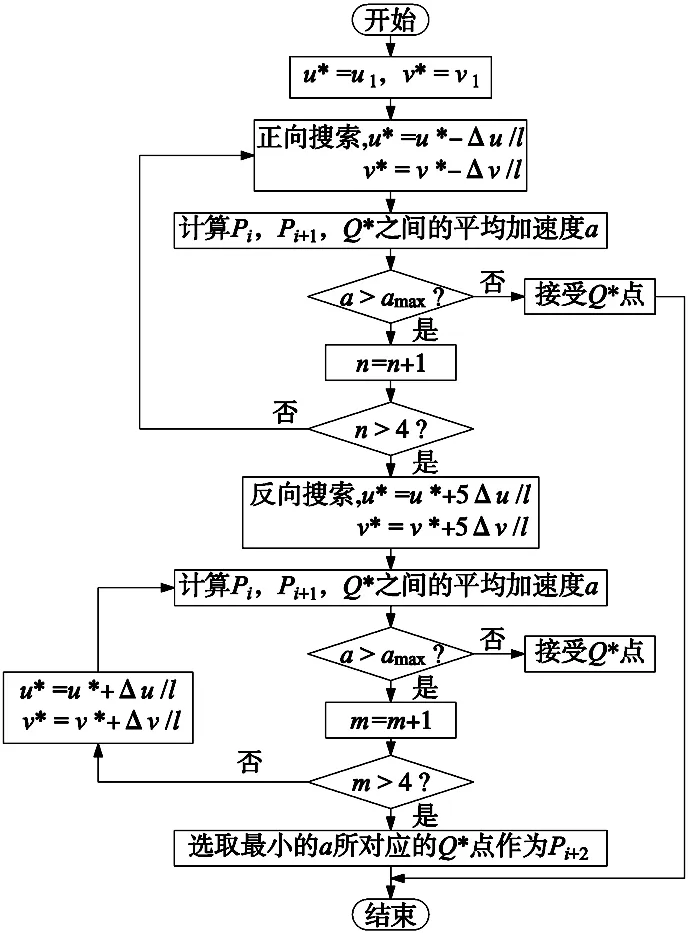
图5 调整Pi+2的流程

调整Pi+2的步骤如下：

①u*=u1，v*=v1，u1,v1为点Pi+2的初始参数值，即由前条刀轨上相应的刀触点得到的点的参数值。

②令u*=u*-Δu/l，v*=v*-Δv/l，得点Q*(u*,v*)。

③将Q*(u*,v*)替换掉Pi+2，计算Pi，Pi+1，Q*(u*,v*)之间平均加速度a。

④若a小于amax，转⑨，否则转②继续搜索。设定最大搜索次数为4，如果到达搜索次数，a仍大于amax，则转⑤。

⑤令u*=u*+5Δu/l,v*=v*+5Δv/l，得点Q*(u*,v*)。计算Pi，Pi+1，Q*(u*,v*)之间平均加速度a。若a小于amax，转⑨，否则转⑥。

⑥令u*=u*+Δu/l，，得点Q*(u*,v*)。

⑦计算Pi，Pi+1，Q*(u*,v*)之间平均加速度a。

⑧若a小于amax，转⑨，否则转⑥继续搜索。设定最大搜索次数为4，如果到达搜索次数，a仍大于amax，则选择最小的a所对应的点作为Q*(u*,v*)。

⑨结束搜索，判断下一刀触点。

3 对UG CAM二次开发实现曲面光顺刀轨生成

UG CAM二次开发工具主要由UG提供的4个应用程序及C++程序组成，UG提供的4个应用程序为UG/Open API、UG/Open UIStyler、UG/Open MenuScript、UG/Open GRIP[10]。UG/Open API是UG二次开发的关键，它的核心包含了约2000个C函数，能实现大部分的UG操作。其中User Exit是UG/Open API中的一个重要概念，用户的程序利用不同的User Exit，就可以以不同的User Exit作为入口点，就能决定该程序在UG进程的哪个阶段被自动激活并运行。本文利用udop(CAM User Defined Operation)作为入口函数，并在本函数中编写代码。

udop函数体如下所示：

extern "C" DllExport void udop( char *param, int *returnCode, int rlen )

{

/*初始化API环境*/

int errorCode = UF_initialize();

int response=0;

if ( 0 == errorCode )

{

if(!UF_CALL(UF_initialize()))

{

/*选择加工曲面 */

do_ugopen_api();

}

if( purpose == UF_UDOP_GENERATE )

{

/*生成曲面刀轨函数*/

generate_optimal_path(path_id);

}

UF_PATH_end_tool_path(path_id);

UF_EVALSF_free(&evaluator);

/*释放API环境*/

errorCode = UF_terminate();

}

PrintErrorMessage( errorCode );

}

UG/Open UIStyler是开发UG对话框的可视化工具，它能够自动生成C模板文件，为用户编程提供便利。下面图6就是利用UG/Open UIStyler自定义的对话框风格。

图6 自定义对话框

在程序中创建并显示对话框的函数如下：

if((errorCode=UF_STYLER_create_dialog("Mach_Para.dlg",TPM_cbs,TPM_CB_COUNT,NULL, &response))!=0)

{

char fail_message[133];

UF_get_fail_message(errorCode,fail_message);

UF_UI_set_status (fail_message);

printf ( "%s ", fail_message );

}

其中Mach_Para.dlg为对话框资源文件，TPM_cbs表示从对话框回调，TPM_CB_COUNT表示回调函数的数量。

4 实例验证

为了验证算法的正确性，通过参考文献[9]拟合一自由曲面得到参数曲面，如图7所示，其中矩形区域为马鞍面，曲面参数方程为：

(10)

图7 参数曲面

在图6设置界面中设定编程公差h=0.05 mm，采用刀具半径为5mm球头刀。最大允许加速度amax取0.004mm/(ms)2，同一刀具轨迹上相邻两刀触点之间走刀时间[11]固定为t，t取12ms。u向走刀，搜索参数l取10。

图8 相邻刀触点之间平均加速度变化曲线

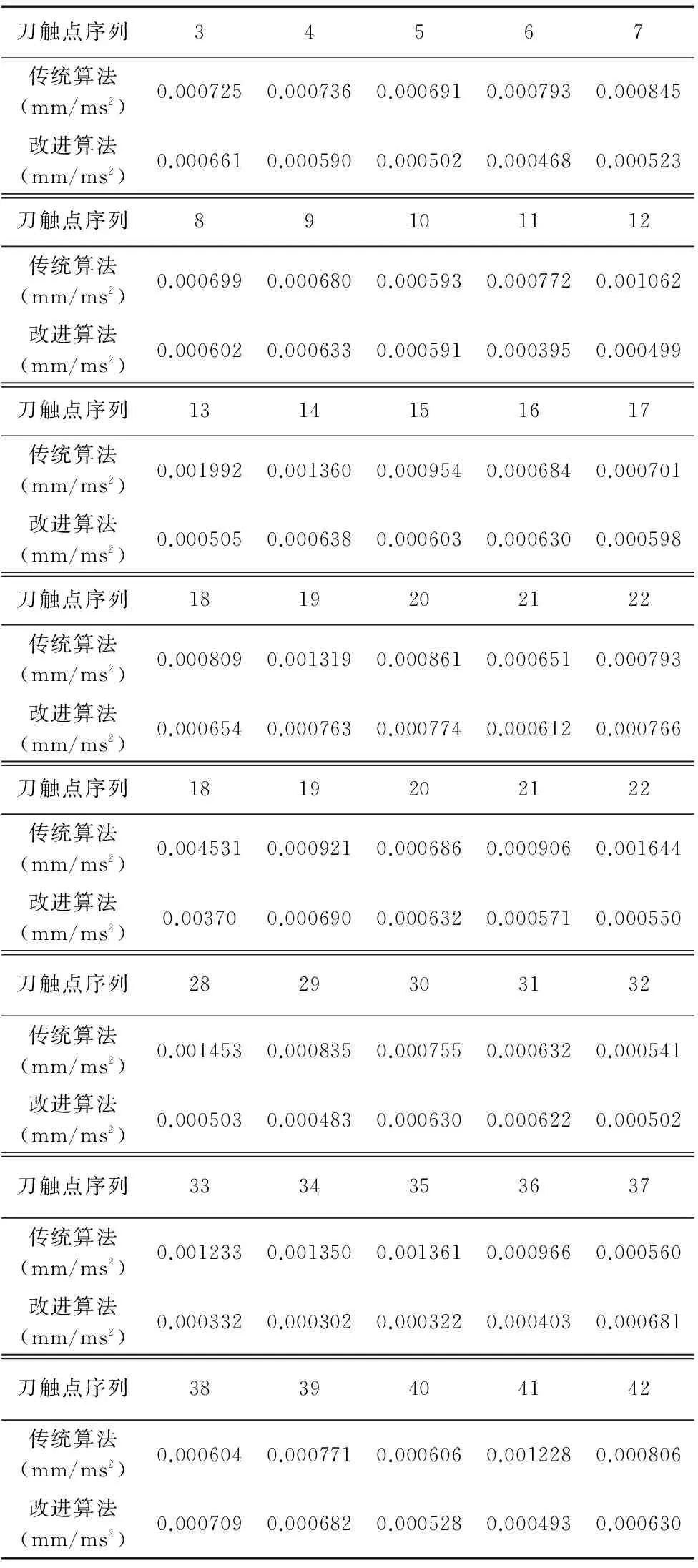
刀触点序列34567传统算法(mm/ms2)0.0007250.0007360.0006910.0007930.000845改进算法(mm/ms2)0.0006610.0005900.0005020.0004680.000523刀触点序列89101112传统算法(mm/ms2)0.0006990.0006800.0005930.0007720.001062改进算法(mm/ms2)0.0006020.0006330.0005910.0003950.000499刀触点序列1314151617传统算法(mm/ms2)0.0019920.0013600.0009540.0006840.000701改进算法(mm/ms2)0.0005050.0006380.0006030.0006300.000598刀触点序列1819202122传统算法(mm/ms2)0.0008090.0013190.0008610.0006510.000793改进算法(mm/ms2)0.0006540.0007630.0007740.0006120.000766刀触点序列1819202122传统算法(mm/ms2)0.0045310.0009210.0006860.0009060.001644改进算法(mm/ms2)0.003700.0006900.0006320.0005710.000550刀触点序列2829303132传统算法(mm/ms2)0.0014530.0008350.0007550.0006320.000541改进算法(mm/ms2)0.0005030.0004830.0006300.0006220.000502刀触点序列3334353637传统算法(mm/ms2)0.0012330.0013500.0013610.0009660.000560改进算法(mm/ms2)0.0003320.0003020.0003220.0004030.000681刀触点序列3839404142传统算法(mm/ms2)0.0006040.0007710.0006060.0012280.000806改进算法(mm/ms2)0.0007090.0006820.0005280.0004930.000630

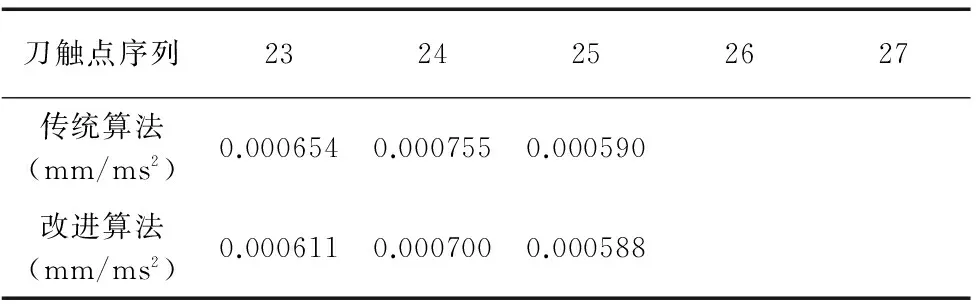
续表

图8为第15行刀轨刀触点处平均加速度变化曲线图，一共45个刀触点。实线由传统算法得到，由于马鞍面部位的曲率变化大，可以看出第23个刀触点处的平均加速度超过了最大允许加速度，刀路变弯，如图9所示。虚线由本文算法得到，对第23个刀触点进行了调整，达到了加速度要求，并且后续刀轨经过同样的调整全部达到要求，如图11所示。

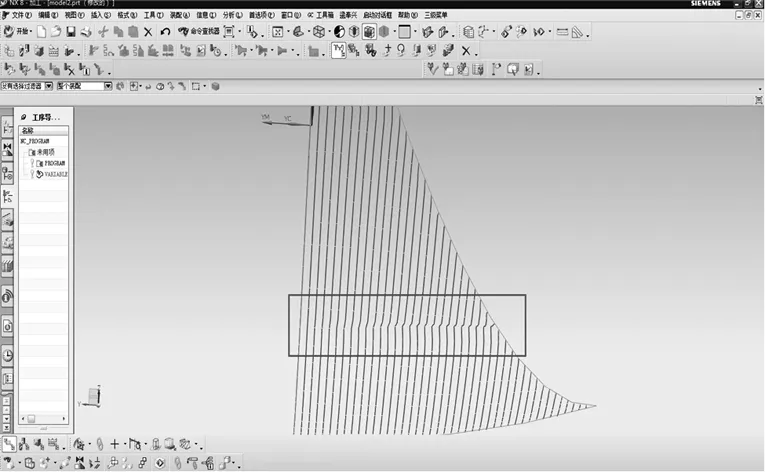
图9 传统等残留高度算法得到的刀具轨迹

图10 传统等残留高度算法得到的刀具轨迹放大图

表1为分别利用传统等残留高度刀轨生成算法和基于加速度约束等残留高度刀轨生成算法得到的第15行刀轨上依次刀触点处的平均加速度值。可看出在第23个刀触点处用前者方法得到的平均加速度值超过了最大允许值，而用后者方法得到了期望值，也可看出在对不符合要求的刀触点调整后，后续刀轨上全部刀触点处的平均加速度都受到影响，从表格看出全部刀触点处平均加速度整体下降。这两种现象足以证明采用基于加速度约束等残留高度刀轨生成算法确实能改善刀轨的光顺性。

图11 基于加速度约束等残留高度算法得到的刀具轨迹

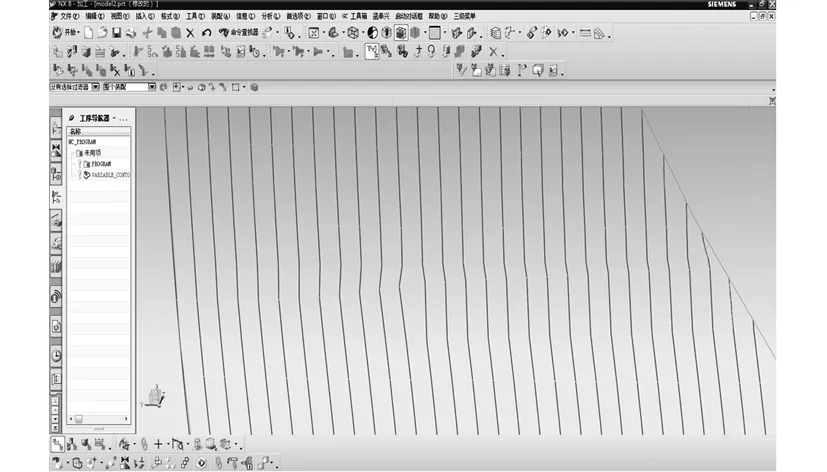
图12 基于加速度约束等残留高度算法得到的刀轨放大图

图10和图12分别为传统算法和基于加速度约束等残留高度刀轨生成算法得到的对应于红色矩形框内的刀路放大图。可看出图10中马鞍面部位刀路存在拐角，这将对加工曲面刀具的稳定性和表面质量产生严重影响。而图12中，基于加速度约束等残留高度刀轨生成算法得到的马鞍面部位的刀路更加光顺，有效的改善了加工质量，避免了刀具的急速磨损。由该算法生成的刀路得到了预期的效果。

5 结论

针对传统的等残留高度算法的缺点，本文算法在传统算法基础上加入了加速度约束条件，提出一种基于加速度约束等残留高度光顺刀轨生成算法。此算法克服了在传统等残留高度算法规划刀具路径出现的刀具轨迹过度弯曲缺点。对UG CAM模块进行了二次开发，并用VC++6.0软件对此算法进行编程，在UG加工模块进行刀路模拟，得到两种算法清晰可见的对

比效果。结果表明，基于加速度约束等残留高度刀轨生成算法较传统等残留高度算法生成的刀路更加光顺，可以得到更高质量的加工效果，可以有效的避免刀具急剧磨损，得到了理想的结果。

[1] 西庆坤. 基于等残留高度的球形曲面的数控加工[J]. 组合机床与自动化加工技术，2015(12):130-132.

[2] 陈银清，郑泽钿.基于Master CAM自由曲面加工刀具路径优化[J].现代制造工程，2014(5):46-51.

[3] 富国亮，张林，魏志强,等.叶轮精加工实例分析[J].现代制造工程，2016(4):80-84.

[4] 赵世田. 自由曲面加工刀具路径轨迹规划算法研究[D]. 南京:南京航空航天大学,2011.

[5] 李占君，王霞，黎振. 基于等残留高度的光顺刀具轨迹规划算法[J]. 机械设计与制造，2010(6):243-245.

[6] 李铁军，李小敏. 一种自由曲面的改进的等残留高度加工方法[J]. 机械设计与制造，2009(1):48-49.

[7] 王幼宁，刘继志. 微分几何讲义[M]. 北京:北京师范大学出版社，2003.

[8] 贺英，陈志同，吴献珍. 复杂曲面宽行加工等参数线刀轨精确搭接方法[J]. 航空学报，2014,35(4):1142-1148.

[9] 白晓亮，张树生，刘军. 曲面拟合过程中的参数值优化方法[J]. 工程图学学报，2004(4):72-76.

[10] 王丹，徐汝锋，陈五一. 基于UG二次开发的宽行加工算法实现[J]. 机床与液压，2008,36(12):32-34.

[11] 冯景春，李宇昊，王宇晗，等. 面向刀尖点速度平滑的五轴联动插补算法[J]. 上海交通大学学报,2009,43(12):1973-1977.

(编辑 李秀敏)

Tool-path Generation Algorithm Based on Constant Scallop-height of Acceleration Constraint

LIANG Feng-xing， DONG Feng， XU Ru-feng， LIU Ji-kai

(School of Mechanical Engineering, Shandong University of Technology, Zibo Shandong 255000, China)

A tool-path generation algorithm of sculptured surfaces based on constant scallop-height of acceleration constraint was presented, aiming at the problem of the tool-path is not smooth when machining the sculptured surfaces with the traditional constant scallop-height tool-path generation algorithm. By judging the average acceleration between the adjacent cutter contact points of the same tool-path to adjust the cutter contact points which does not conform to the acceleration condition, so as to ensure the smoothness of the tool-path. Based on this algorithm, the VC++6.0 and secondary development platform of UG OPEN/API were used to prepare the program. The parametric surface obtained by fitting freeform surface is processed and the tool-path simulation was carried out in UG (Unigraphics NX) CAM module. The results show that the algorithm can effectively improve the smoothness of the tool-path，and the ideal result is obtained.

the theory of acceleration constraint;constant scallop-height;tool-path ; the second development of UG OPEN/API

1001-2265(2017)05-0052-05

10.13462/j.cnki.mmtamt.2017.05.014

2016-08-19；

2016-10-19

梁奉兴(1989—)，男，山东济宁人，山东理工大学硕士研究生，研究方向为复杂曲面多轴数控加工技术，(E-mail)619852506@qq.com。

TH161;TG506

A