极坐标圆弧插补算法的计算仿真与实验验证*

来旭辉，许 燕，周建平

(新疆大学 机械工程学院，乌鲁木齐 830047)

极坐标圆弧插补算法的计算仿真与实验验证*

来旭辉，许 燕，周建平

(新疆大学 机械工程学院，乌鲁木齐 830047)

为减少铸造成型开模周期提高零件生产效率和质量，搭建了极坐标成型平台。阐述了极坐标相对直角坐标的优势，根据极坐标堆焊成型设备的结构综合逐点比较法及时间分割法，对极坐标下的圆弧插补算法进行了研究和探索，提出了极坐标模式下的逐点比较插补算法，对极坐标特有的插补特殊点和关键点的插补精度进行了优化，并编写可视化软件对插补过程仿真分析。最后设计圆筒插补实验通过对比得出该算法稳定可行。

极坐标成型；堆焊成型；逐点比较法；可视化软件

0 引言

金属快速成型是先进制造技术的重要分支，按照加工方式的不同可以分为电弧加工，激光加工和等离子加工等，诸如此类轮廓加工设备大多为直角框架结构或回转悬臂结构[1]，其中直角框架结构是在直角坐标的基础上进行开发研制的，对于回转悬臂结构则更适合结合自身特点以极坐标为基础进行配套软件开发，基于极坐标的加工设备可以很好地实现对圆锥曲线，阿基米德螺旋线等用极坐标参数描述的轨迹的拟合[2]，可以在同等条件下加工出比直角坐标精度更高的工件，旋转结构可快速对零件内部进行圆弧填充，保证成型后的零件具有良好的径向力学性能[3]，并且表面轮廓以弧线过渡，有效地避免了阶梯状外形的出现，成型后的金属零件可以直接或经过少量机械加工后就投入使用。

1 极坐标堆焊成型平台简介

现有的插补算法大多为直角坐标模式，采用直线段逼近二维面单元的方法[4]。而极坐标插补是以弧线拟合二维轮廓并以圆弧填充为主，成型后工件有较高的径向力学性能，且焊缝间为冶金结合，因此零件内部组织均匀，致密度高。较之激光成型等设备开发周期短，成本低[5]，对于精度要求不高的场合有明显的优势。可分担大型零部件铸造的工作，且不受开模周期和场地的限制[6]。

极坐标堆焊成型平台如图1所示，电机1通过同步轮带动双焊枪做周向运动可对模型的区域轮廓快速进行整圆或圆弧填充，电机2和电机3驱动焊枪径向运动，电机4带动成型平面在z向做间歇性进给，4个电机协调配合构成一个空间的柱坐标区域。采用柱坐标加工方式成型的工件具有良好的径向力学性能，且单道焊缝间为冶金结合，致密度良好[7]。模型轮廓用柱坐标插补方式勾勒，减少了以往的阶梯拟合的尖角数量，实现零件轮廓光滑过度。后面将以柱坐标数学模型，对极坐标堆焊成型设备的进给控制软件进行讨论和验证。

图1 极坐标焊枪堆焊成型平台

2 极坐标逐点比较法插补过程分析

2.1 极点位于待插补圆外

极坐标下的圆弧插补与直角坐标类似，都是通过控制两根轴协调进给达到拟合待加工曲线的目的，不同的是极坐标下不存在四个象限，取而代之的是4个改变插补方向的变向点，为此将整圆的插补过程分为4个阶段：1→2、2→3、3→4和4→1，具体位置如图2所示。并且这四个点随着圆弧的位置和大小在不断变化，属于每个圆弧的固有特征。

圆心的极径为ρr，极角为θr，由图2可以看出变向点1，3与圆心共线，则变向点1，3的极径为：

(1)

根据变向点3，4的三角关系可以求得：

(2)

以极点在圆外的整圆插补为例介绍整圆的4个变向点，假设插补起点在圆外以此推导一般插补方法。

图2 变向点的选取 图3 极点位于圆外

当插补点位于1→2阶段，径向轴向+ρ方向进给，焊枪进入到理论圆周内，停止径向脉冲进给，轴向轴向-θ方向旋进直至焊枪位于圆外停止插补，第二阶段重复前述过程到2点时停止，四个阶段的插补进给方向如表1所示。

表1 插补进给方向

极坐标下圆系方程为：

(3)

定义误差判别式F为：

(4)

+ρ引起的误差变化：

(5)

同理ΔF取值的其他情况：

(6)

2.2 极点位于待插补圆内

当极点位于插补圆内时，插补变向点为两个，如图4所示。当焊枪处于圆外且起点在1→2阶段，则旋转轴向+θ方向旋转，当点处于圆内时停止插补，径向轴向+ρ方向进给，当进入2→1阶段的循环模式时，先向-ρ方向进给，减小极径，进入圆内后绕+θ方向旋转。当焊枪处于圆外起点在1→2阶段分析方法类似。

此时变向点1，2位于圆心和极点的延长线上，如图4所示。变向点的坐标为：

(7)

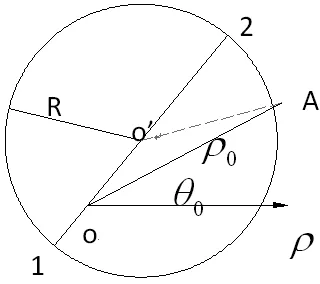
图4 极点位于园内

当圆弧经过极点时，为了减小判断次数，将变向点2的极角修正为：

bian1_θ=θr+0.5π

(8)

2.3 特殊点圆弧插补误差处理

按照极坐标的特性将圆弧的插补过程按照极点与圆的位置关系分别定义为4个阶段和2各阶段，对于不过原点的弧线插补，当插补进行到靠近2，4点时，容易脱离变向点的角度限制，导致程序进入死循环，因此采用修正系数K2=0.99，K4=1.01对约束条件进行放宽，帮助程序越过插补死点。

对于圆心极径等于插补圆半径且圆弧过极点情况，当插补靠近极点时ρ方向进给会急剧减小，θ方向角度会越来越大，致使程序沿极点走出一条射线。因此当加工点与原点的距离小于一个进给步长时将当前点的极径设置为一个进给步长，将当前点的极角设置为变向点1的角度增加π，以将当前点限制在圆内。

2.4 终点判别方法的选择

终点判断算法是整个软件精度的重要组成部分[8]，常用的终点判断方法有角度法和距离法，距离判断法是通过比较当前加工点的弦长与终点之间的距离来甄别加工终点。而同一弦长对应的优弧劣弧判断方法繁琐复杂且判别误差较大，因此采用以角度法来作为判断条件。

角度判断法的的关键是保证当前点从起点开始到插补结束点的极角是单调变化。对于极点在圆内的弧线插补，当终点极角小于起点极角时，将终点角度修正为es+2π。

根据圆和极点的位置关系将整个极坐标平面分为4个区域，如图5所示。对于极点在圆外的情况，加工点的极角在(bian2_c,bian4_c)的范围内，角度变化不连续，终点判断非常困难或者需要加很多的约束条件，为此提出坐标变换的思想，移动极轴与极点到圆心处判断。

图5 极坐标下坐标变换

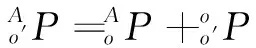
(9)

A点极径：

《调剂管理办法》指出，“三区三州”（即西藏、四省藏区、南疆四地州和四川凉山州、云南怒江州、甘肃临夏州）及其他深度贫困县城乡建设用地增减挂钩节余指标由国家统筹跨省域调剂使用。国家下达调剂任务，确定调剂价格标准，统一资金收取和支出。有关部门根据有关省（区、市）经济发展、土地利用和贫困人口等情况，报经国务院同意，将跨省域调剂节余指标任务下达有关省（区、市）。财政部统一收取帮扶省份调剂资金，统一拨付深度贫困地区所在省份。调剂资金支出要优先和重点保障产生节余指标深度贫困地区的安置补偿、拆旧复垦、基础设施和公共服务设施建设等。

(10)

所以A点的极角：θA=θs+arcsin∠o′Ao

当A点处于图5b：θA=θs-arcsin∠o′Ao

当A点处于图5c：θA=θs+arcsin∠o′Ao

当A点处于图5d：θA=θs-arcsin∠o′Ao

转换后则可直接在o′坐标中应用圆心在圆内的判断方法进行终点判断。

3 基于pascal语言的软件仿真与实验验证

3.1 插补软件介绍

图6 插补流程图

以上内容提出了极坐标下圆弧插补的基本思路和方法，为了探究其可靠性和可行性，根据图6所示的编程思路，编写界面程序对整个算法进行验证。插补控制软件界面如图7所示。软件包括运动控制，状态监测与显示和插补控制三大模块，能实时采集堆焊过程中的位置与速度信息；可动态显示插补过程，及当前插补数据；支持与插补图形相关的放大缩小操作，可对插补点实时标记，便于跟踪观察。

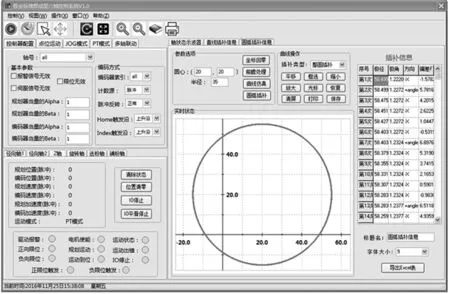
图7 插补控制软件

试验选用外径为75mm，内径65mm，高度为20mm的模型对极坐标圆弧验证。设置焊接速度为165mm/min，气体流量为10L/min，送丝速度为100cm/min。在单道圆环零件堆焊成型的过程中，每堆焊完成一层后对成型轨迹的高度进行测量，第一层的高度为2.1mm，第二层成型完的高度为4.0mm，第二层之后的9层的高度基本都在1.9～2.1mm之间。在堆焊成型的过程中同样存在误差，最终导致后续的成型轨迹的余高会在一定的范围内浮动，但是对整体零件的成型质量影响不大。经过测量得到成型零件的外径最大值为76.4mm最小值为74.5mm，外径的误差在1.9mm(误差在2.5%以内)。内径的最大值为66.2mm，内径的最小值为64.4mm，内径的误差在1.8mm(误差在3%以内)。成型零件的高度最大值为21.3mm，最小值为19.8mm，误差为1.5(误差在7.5%以内)，最终成型零件如图8所示。

图8 单道多层验证试验

南昌大学张华教授的团队从事于直角坐标下的TIG熔焊成型研究，以传统逐点比较法插补配合模糊PID焊接参数预测与BP网络优化也取得了较好的成型效果，经过机械加工处理后的圆筒效果如图9所示。起弧焊接电流为110A，焊接速度为150mm/min，测得圆筒高度为15mm，外径45mm，内径32.4mm[10]。

图9 圆柱堆积成型

结合图8对比可以看出，极坐标插补算法可在减少成型中的参数修改而实现圆弧的平稳成型，保证单道焊缝的成型精度，并保证多道焊缝成型的误差在可控的范围内， 通过协调焊接电流，送丝速度和焊接速度，可实现模型表面相对光滑。

3.3 插补效率测试

选取直径80mm的圆进行插补效率测试，当插补精度为0.2mm时，共执行2432步。采取5种不同精度，在工控机上测试，结果如图10所示。

图10 插补效率测试

当插补精度为0.6mm，插补用时短且执行步骤少，精度在0.2～0.6mm之间时，插补时间随着精度提高明显增加，因此选用0.6mm作为极坐标插补偏差判别量。

4 总结

结合直角坐标系下的逐点比较法和时间分割法，提出了适用于极坐标成型设备的圆弧插补算法。设计了单道多层成型试验，通过实验得出以下结论：

(1)本插补算法启停平稳，代码执行效率高。能够实现极平面内任意位置的圆弧插补，可顺利越过极坐标中的插补死点和特殊点。

(2)插补控制可在一定程度上减少焊接参数的更改，保证零件稳定成型。

[1] 李银华.基于离心角变化的椭圆插补算法研究[J].组合机床与自动化加工技术,2015(12):39-42.

[2] 吴新淼.基于直线逼近的曲线插补算法研究[J].机械工程师,2015(8):71-74.

[3] 王耀庭.高速嵌入式数控系统速度前瞻控制算法的研究[J].机械科学与技术,2014,33(12):1850-1853.

[4] TANDEM and GMAW Twin Wire Welding of Q690 Steel Used in Hydraulic Support[J]. Journal of Iron and Steel Research(International),2012(5):79-85.

[5] 刘振超.五轴木工数控机床的刀具补偿和插补误差分析[J].木材加工机械,2014(5):22-25.

[6] 黄国辉.基于DSP的NURBS曲线实时插补数控系统的研究[J].机床与液压,2013,41(23):40-44.

[7] 杨林,张承瑞. 基于时间分割的前加减速快速插补算法[J].制造技术与机床,2008(9):93-96.

[8] 殷晨晨,吴文江.基于弧长的椭圆插补新算法[J].组合机床与自动化加工技术,2012(4):2-4.

[9] 范希营,郭永环.提高数控系统基准脉冲直线插补速度及精度的研究[J].制造技术与机床,2010(3):89-91.

[10] 张光云. TIG熔焊成型中焊缝几何尺寸的建模与控制[D].南昌:南昌大学,2008.

(编辑 李秀敏)

Computational Simulation and Experimental Verification of Polar Circular Interpolation Algorithm

LAI Xu-hui，XU Yan, ZHOU Jian-ping

(School of Mechanical Engineering, Xinjiang University, Urumqi 830047,China)

In order to reduce the casting mold cycle and improve the production efficiency and quality of the parts, a polar coordinate welding forming equipment was developed.The advantage of polar coordinates relative to rectangular coordinates is expounded, So we combines the structure of polar coordinate FDM equipment with the interpolation theory of the point by point comparison method to research and explore the arc interpolation algorithm in polar coordinates, we put forward a complete set of interpolation algorithm and optimized the interpolation precision of the special points and the key points,and then simulate the interpolation process by visual software. Finally, the design of cylinder interpolation experiments show that the algorithm is stable and feasible.

polar forming; surfacing forming; point by point comparison; visualization software

1001-2265(2017)05-0032-04

10.13462/j.cnki.mmtamt.2017.05.009

2016-10-20;

2016-12-18

自治区科技人才培养资助项目(gn2015yx008)

来旭辉(1992—)，男，陕西兴平人，新疆大学硕士研究生，研究方向为金属快速成型与微机控制，(E-mail)2374999541@qq.com；通讯作者：许燕(1975—)，女，浙江东阳人，新疆大学教授，研究方向为数字化设计及风力发电机组研究，(E-mail)lilixiu_z@163.com。

TH16;TG65

A