采用傅里叶描述子和支持向量机的服装款式识别方法

李 东， 万贤福,2， 汪 军,2(. 东华大学 纺织学院， 上海 20620； 2. 东华大学 纺织面料技术教育部重点实验室， 上海 20620)

采用傅里叶描述子和支持向量机的服装款式识别方法

李 东1， 万贤福1,2， 汪 军1,2
(1. 东华大学 纺织学院， 上海 201620； 2. 东华大学 纺织面料技术教育部重点实验室， 上海 201620)

为解决当前服装款式识别领域中，服装轮廓特征提取技术较复杂，其分类方法的效率低、适应性差等问题，提出一种新型的服装款式的识别方法。首先创建了一个服装图像样本库，并从这些服装图像中提取服装轮廓，然后使用傅里叶描述子描述服装的轮廓特征，以多分类支持向量机进行分类。结果表明，该方法能够准确提取服装轮廓，傅里叶描述子的识别效果优于Hu不变矩和融合特征(Hu不变矩和傅里叶描述子)；对傅里叶描述子进行主成分分析不能提高识别准确率；支持向量机的分类效果优于极端学习机；该方法能够达到95%以上的识别率，尤其对轮廓特征明显的款式有更好的识别率。

服装款式识别； 傅里叶描述子； 支持向量机； Hu不变矩； 主成分分析； 极端学习机

随着大数据时代的来临，商家通过机器视觉技术识别消费者着装款式，将有助于商家捕捉各客户群体的消费趋势，制定出有针对性的产品组合、营销计划和商业决策。此外，随着人脸计算机识别技术的普及，提取人脸特征并结合服装款式特征，将会提高身份认证的精确度。

服装款式是由服装的外部轮廓和内部细节变化构成的，反映了服装结构的形状特征，不包含颜色和纹理特征[1]。寻找一种有效的方法描述服装的款式特征并且快速精确地分类是服装款式识别领域的研究重点。尽管国内外学者做了一些服装款式特征提取与分类的探索工作，但由于特征提取技术和模式识别技术的复杂性，服装款式识别方法的适应性和实时性仍有待进一步提高。李克兢等[2]提取服装设计平面图轮廓点，将衣片轮廓半自动地拆分并进行数学描述。Hussain等[3]提出一种算法，自动提取杂志或书上的服装款式平面图，由二维服装设计平面图转换为三维服装衣片，这种算法依赖于服装衣片精确分割和轮廓的尺寸测量。Wang等[4]提出一种基于模糊理论的服装款式分类方法，分析服装轮廓点的特点，根据模糊理论将款式轮廓点自动分类，该方法是针对局部轮廓片段的识别，并不是整体的轮廓。An等[5]提出一种服装设计平面图的分类方法，使用小波傅里叶描述子(wavelet fourier descriptor，WFD)描述轮廓特征，对WFD降维后训练了极端学习机分类器(extreme learning machine，ELM)，进行服装设计平面图的分类。由于WFD特征向量之间的相似度对比方法较复杂，且依赖于目标物体轮廓的复杂度，因此，WFD并不适合形状的实时分类[6]。Hou等[7]在服装图像检索的研究中提出使用融合特征(Hu不变矩和傅里叶描述子)来描述服装的形状特征，通过计算欧式距离来判断形状的相似性。

傅里叶描述子(Fourier descriptor，FD)[8]是基于傅里叶理论提出的一种计算简单、抗噪性强的形状特征描述方式。由于其每个描述符都有具体物理意义，不仅能够兼顾全局及局部特征，且特征匹配简单，相比而言更适合服装款式的实时分类[6]。欧式距离虽然是一种简单有效的相似性判断方法，但是在处理复杂特征的多分类问题上与支持向量机(support vector machine，SVM)[9]等机器学习分类器相比效果较差，同时SVM由于其非线性映射的理论基础避免了“维数灾难”，因此具有较好的鲁棒性。鉴于上述原因，本文提出一种新的基于傅里叶描述子和SVM的服装款式识别方法，能够快速有效地进行多类服装款式的识别。

1 预处理与轮廓特征提取及分类

基于傅里叶描述子和SVM的服装款式识别方法流程如图1所示。通过对服装图像的预处理，获取服装的外部轮廓，使用傅里叶描述子提取服装轮廓特征，以傅里叶描述子特征向量训练SVM分类器，实现服装款式的识别。

1.1 服装图像预处理

本文选用白色背景的服装图像进行预处理。服装图像的预处理包括服装图像分割和边缘检测，经过预处理后获得服装轮廓图像，以供后续轮廓形状特征的提取。预处理过程如图2所示。1)将服装图像转化为灰度图像并进行灰度的线性变换，增强灰度图像的对比度；2)使用最大类间方差(Otsu)法[10]进行二值化；3)进行形态学开运算处理和填充空洞，最大的8连通区域就是服装图像；4)使用Canny算子进行边缘检测获取服装的外部轮廓。

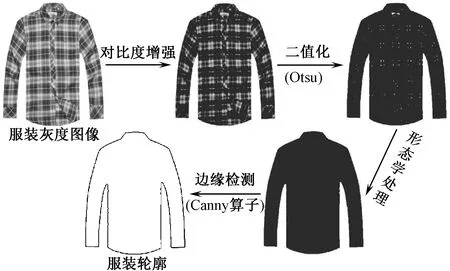
图2 服装图像的预处理过程Fig.2 Pretreatment process of clothing image

1.2 服装轮廓的傅里叶描述

采用预处理得到的服装轮廓信息，由轮廓图像上各像素点的坐标排成序列来表示。轮廓像素点采用坐标b(k)表示，b(k)=(xk,yk)。其中xk和yk分别为横坐标值与纵坐标值，k=0,1,2,…,K-1；K为轮廓像素点总数。将坐标写成复数形式，则有b(k)=xk+jyk，j为虚数单位。将复数坐标序列b(k)进行离散傅里叶变换可得到服装轮廓的傅里叶描述序列：

式中u=0,1,2,…,K-1。

为得到对图像平移、旋转和缩放不敏感的傅里叶描述子，对a(u)进行标准化，得到标准化傅里叶描述子：

式中：u=2,3,…,K-1;v=1,2,…,K-2。将s(v)写成向量形式，则为服装轮廓的傅里叶描述子特征向量。傅里叶描述子特征向量的低频分量(即排序靠前的分量)表示形状总体特征，高频分量(即排序靠后的分量)表示形状细节特征。在进行分类时，需要选取适当的特征向量长度。图2中的服装轮廓提取傅里叶描述子特征向量后，分别选取前10、20、40个分量进行重构，得到的服装轮廓如图3所示。由图可知：长度如果过短，则不足以表示轮廓图像的形状特征；而如果过长，则会造成信息冗余，识别计算量增加。

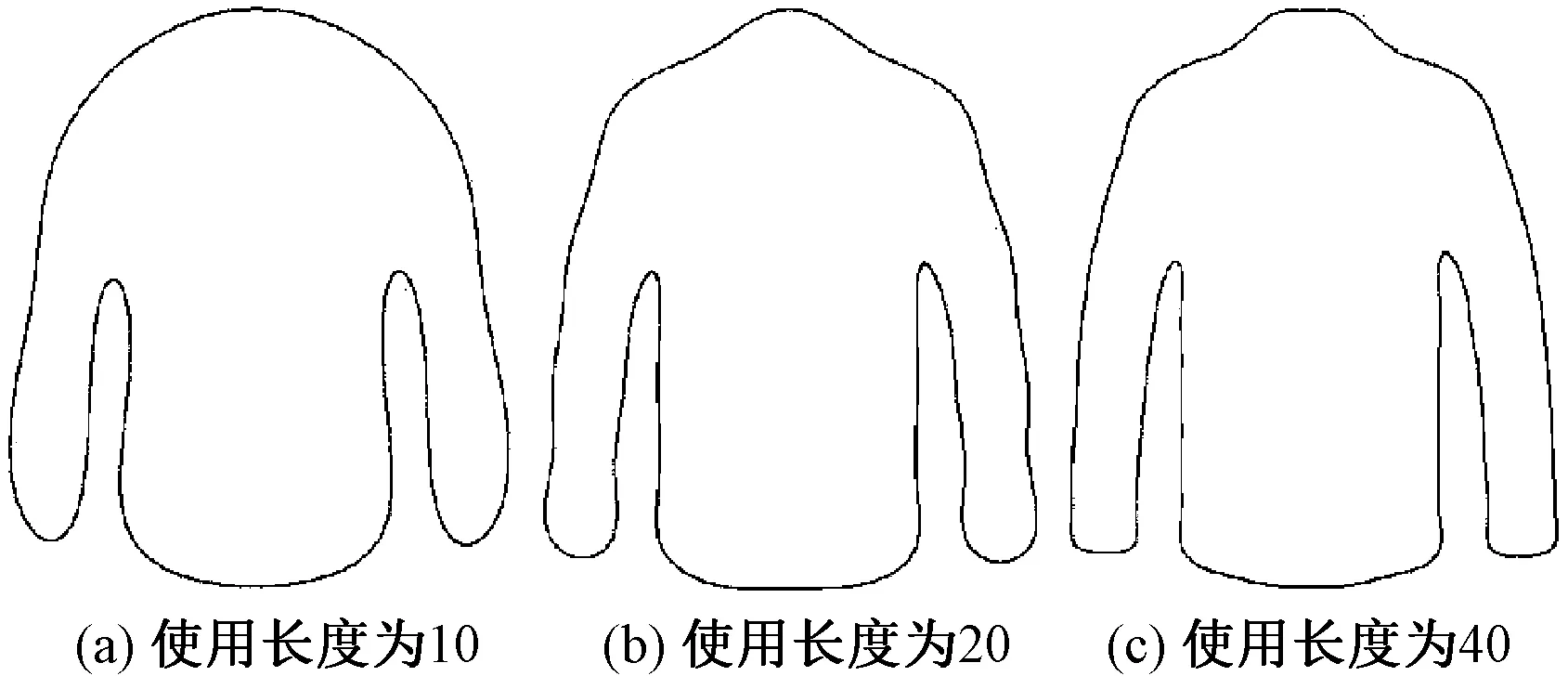
图3 傅里叶描述子进行重构的轮廓Fig.3 Reconstructed contours described by Fourier descriptors. (a) Length of 10; (b) Length of 20; (c) Length of 40

1.3 基于SVM的服装款式分类

在傅里叶描述子提取服装轮廓特征后进行服装款式分类，选用SVM作为服装款式特征的分类器。SVM是一种有监督的学习模型，可学习不同类别的已知样本特点，进而对未知样本进行预测。其基本思想是建立一个分类超平面，使得样本空间中正例和反例之间的距离最大化。其本质上是一个二分类的算法，但也可扩展成多分类的分类器，本文采用LibSVM工具箱[11]进行服装款式的SVM多分类。

服装款式SVM分类系统流程如图4所示。首先将训练集描述服装轮廓特征的傅里叶描述子特征矩阵以及服装款式类别标签作为输入；SVM分类器的核函数为径向基函数，使用网格搜索法[12]进行分类器中惩罚参数和核参数的寻优，其中惩罚参数的范围是[-8,8]，核参数的范围是[-8,8]，步长为1；然后使用网格搜索法得到的最优参数、训练集傅里叶描述子特征矩阵及类别标签，训练得到SVM分类器；最后将测试集傅里叶描述子特征矩阵输入到SVM分类器中得到测试集服装款式预测类别，与测试集实际款式比较即可得到分类的准确率。

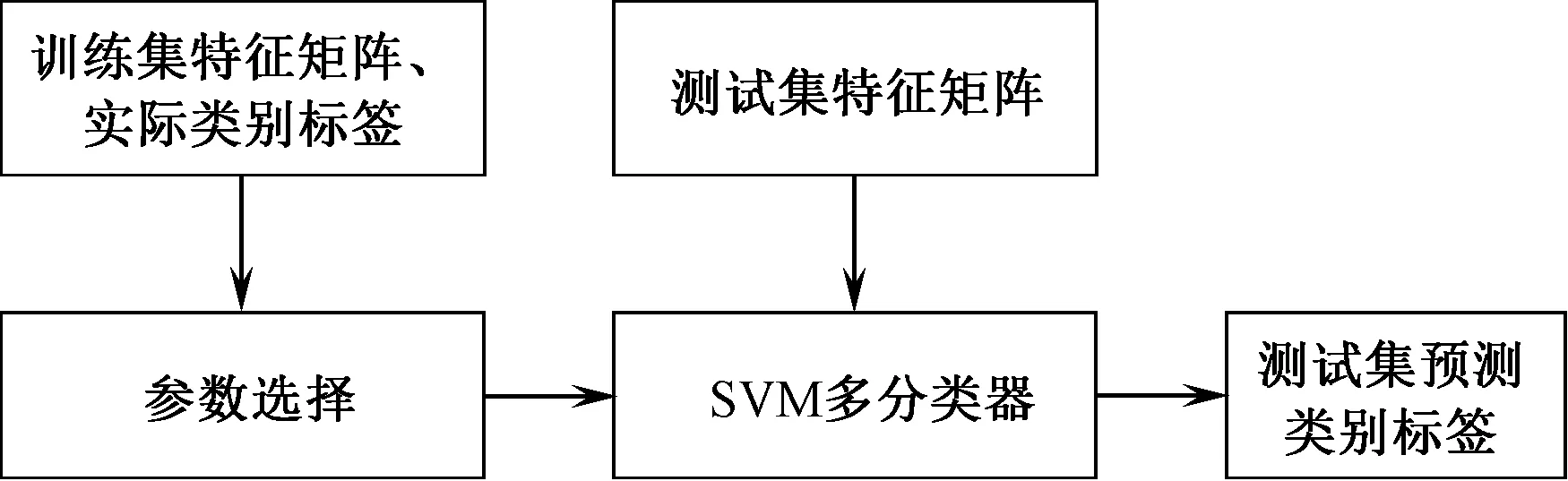
图4 SVM分类系统流程图Fig.4 Flow chart of SVM classification system

2 实验描述

采用MatLab R2014a编程实现，基于DELL Inspiron 14-5439笔记本电脑的Win7系统(Intel(R) Core(TM) i5- 4200CPU，2.3 GHz，4 GB RAM)。由于目前并没有统一的服装图像样本库，本文创建了一个新的样本库，包含的650个服装样本图像收集自天猫网(www.tmall.com)，均为白色背景且平整摆放的单件服装图像，涵盖了短袖T恤、长袖T恤、长袖衬衣、外套(夹克衫、皮衣和翻领短风衣等)、西装上衣、短裤、长裤和短袖连衣裙等8种最常见的服装款式。8种款式的典型样本如图5所示。针对样本库进行10次识别实验，每次识别实验都随机抽取样本库中60%的样本作为训练集，剩余的40%作为测试集，组成一个样本集[训练集；测试集]，样本集中各款式数量如表1所示。

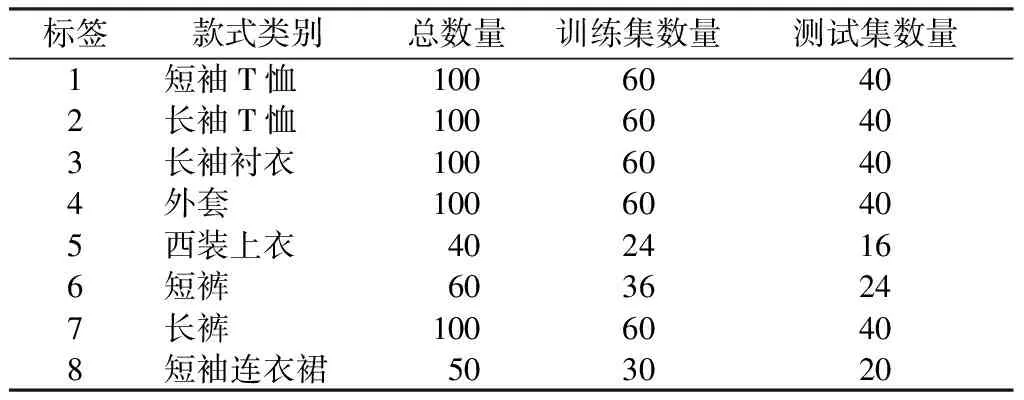
表1 服装图像样本集Tab.1 Database of clothing images

为选取适当的傅里叶描述子特征向量长度，本文进行了预实验，分别采用不同的傅里叶描述子特征向量长度(n=1,2,3,…，50)，从s(v)序列中选取前n个分量作为特征向量。以此对样本集进行SVM分类器训练和分类测试，其准确率如图6所示。由图可知，长度为20时的识别准确率最高，因此，特征向量长度确定为20。

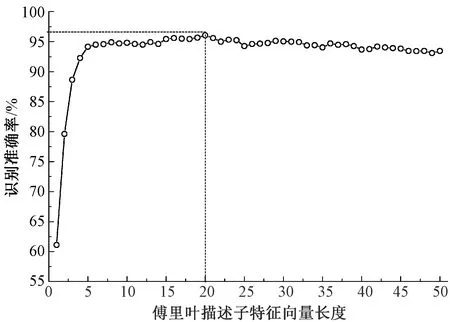
图6 傅里叶描述子特征向量长度与识别准确率的关系Fig.6 Relationship between FD vector length and recognition accuracy

3 结果和讨论

3.1 服装款式识别结果比较

总体识别率在95%以上，各款式识别率如表2所示。长裤、短裤和短袖T恤等款式的识别率较高(96%以上)，主要是因为其形状特征与其他款式差别较明显。西装上衣、外套和长袖衬衣相比其他几类识别率低，因为三者的差别主要在领子和门襟等形状细节上，而没有体现在外观轮廓上。

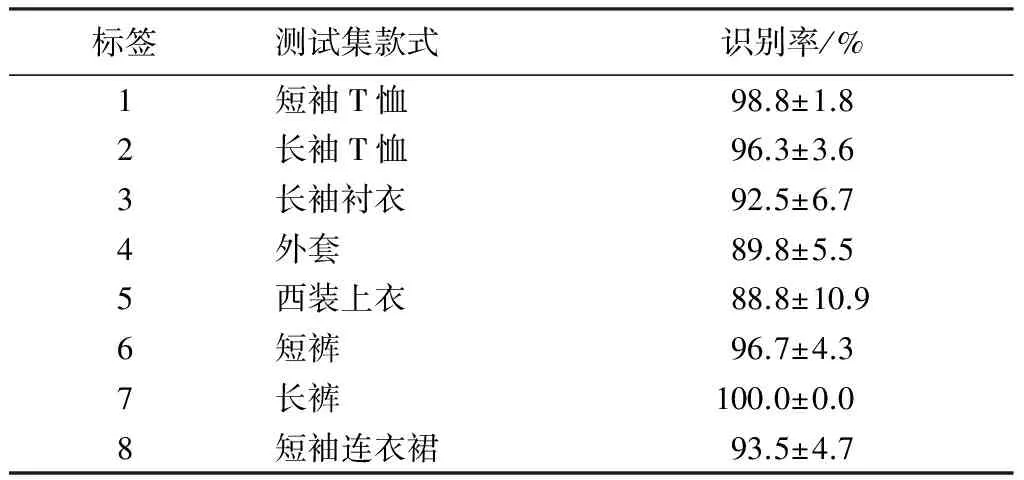
表2 测试集款式识别结果Tab.2 Style recognition results for test set

3.2 不同特征提取技术识别效果比较

为验证傅里叶描述子描述形状特征的优势，本文对比分析了Hu不变矩和融合特征法描述服装款式特征的识别效果。

Hu不变矩[13]是以图像归一化中心不变矩的形式来表示图像形状特征，对图像具有旋转、缩放和平移不变性的7个Hu不变矩特征向量为：φ=[φ1,φ2,φ3,φ4,φ5,φ6,φ7]。融合特征法是将Hu不变矩和傅里叶描述子2个特征向量采用串行特征融合的方式融合，得到融合特征向量f=[φ,s(v)]。由于不同特征表达的物理意义和取值范围不同，所以采用融合特征分类时需要对特征向量进行内部的归一化。特征向量的归一化采用高斯归一化，即对特征矩阵f计算其每个分量的均值μ和标准差σ，将其每个分量归一化至[-1,1]区间。归一化后的融合特征为：r=(f-μ)/σ。

对样本集分别提取傅里叶描述子特征、Hu不变矩特征和融合特征，进行SVM分类训练与测试，10次实验的识别率结果如图7所示。结果显示，傅里叶描述子的识别效果明显高于Hu不变矩。同时，融合特征法识别准确率与傅里叶描述子相比略低1%左右，说明Hu不变矩和傅里叶描述子的融合并不能提高识别效果；因此，采用单一的傅里叶描述子表征服装的款式即可。

图7 不同特征提取技术识别效果对比图Fig.7 Comparison of recognition accuracy for different feature extraction techniques

3.3 主成分分析识别效果比较

主成分分析(principal component analysis，PCA)是将多个变量进行线性变换以选择较少数量的重要变量表示整体的方法[14]。对多维数据分析时，数据经过主成分分析后能够降低维度，减少计算量。

为验证服装款式分类前是否需要对傅里叶描述子进行主成分分析，本文对比分析了PCA降维前后对SVM分类效果的影响。主成分分析时分别选取累计贡献率为95%和99%的特征向量作为主成分。10次实验对比结果如图8所示。结果表明，傅里叶描述子特征进行PCA后的SVM分类准确率显著降低。这可能是由于傅里叶描述子特征向量各分量中的非线性相关的成分与分类特征关系紧密，降维造成了部分特征信息的丢失，因此，采用本文的方法对傅里叶描述子进行主成分分析并无必要。

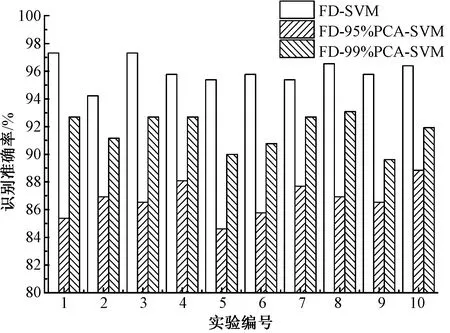
图8 PCA前后识别效果对比图Fig.8 Comparison of recognition accuracy before and after PCA

3.4 支持向量机与极端学习机分类效果比较

Huang等[15]提出的极端学习机(extreme learning machine，ELM)，通过对单隐层神经网络的输入权值和隐层节点偏移量随机地赋值，经过一步计算即可求解出神经网络的输出权值。ELM能够极大地提高网络学习的速度和泛化能力，具有很高的运算速度优势，但却不可避免地造成过拟合的隐患，使分类效果降低。

为验证ELM对服装款式傅里叶描述子特征的分类效果，本文使用了elm_kernel工具箱[16]进行ELM分类实验。ELM分类器的核函数为径向基函数，核参数为100，正则项系数为1。样本集提取傅里叶描述子特征向量后分别进行ELM与SVM分类实验，10次实验计算耗时与准确率的对比结果如图9所示。可看出，SVM算法在速度上达到了ELM的速度，而分类准确率相比ELM则大幅提高，达95%以上。

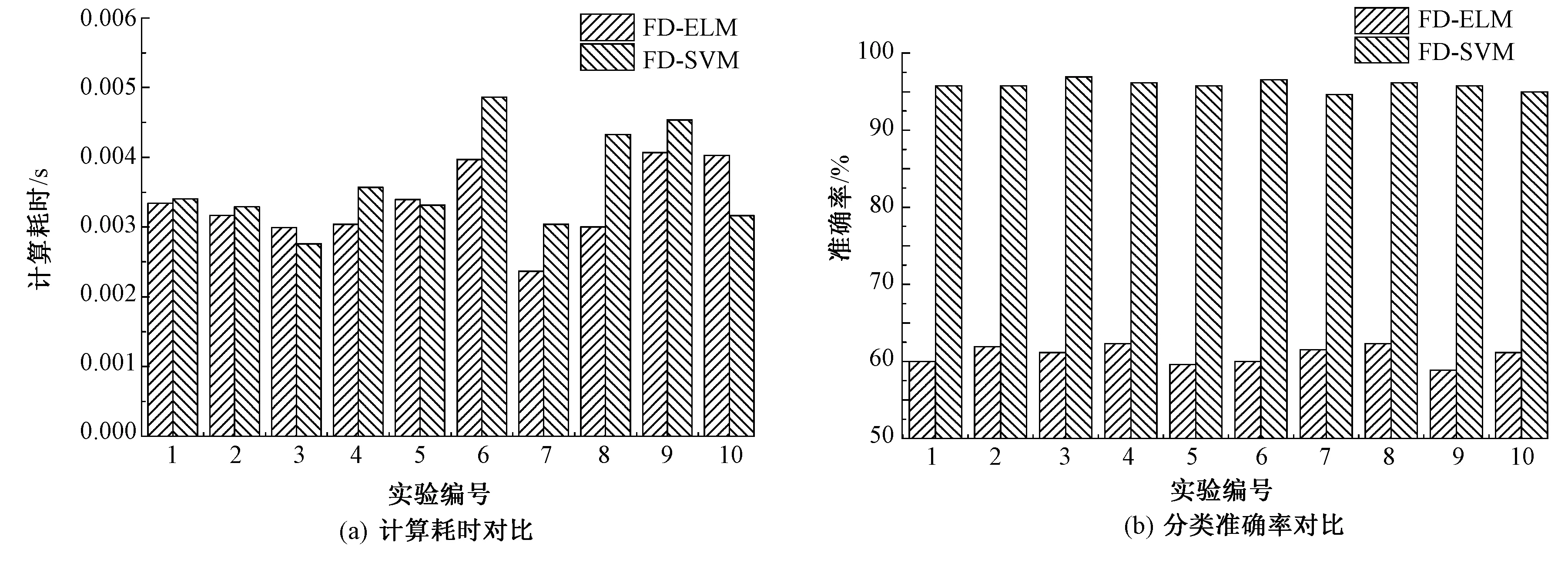
图9 ELM与SVM对比Fig.9 Comparison of ELM and SVM. (a) Computation time; (b) Classification accuracy

4 结 论

本文提出了一种基于服装轮廓识别服装款式的新方法，即通过傅里叶描述子表征服装轮廓特征，并且采用多分类SVM进行分类。通过对650件衣服的样本库进行实验测试发现：傅里叶描述子比Hu不变矩和融合特征法更能表达服装的款式特征；且无需对傅里叶描述子进行主成分分析降维；与ELM分类器相比，SVM更为出色，该方法可达到95%以上的款式识别率。

FZXB

[1] 燕平. 服装款式设计[M]. 重庆:西南师范大学出版社, 2011:3-4. YAN Ping. Clothing Design[M]. Chongqing: Southwest China Normal University Press, 2011:3-4.

[2] 李克兢, 刘哲. 服装图片款式计算机分析技术研究[J]. 上海纺织科技, 2005, 33(1): 53-55. LI Kejing, LIU Zhe. Research on computer analyzing techniques for garment image style [J]. Shanghai Textile Science & Technology, 2005, 33(1): 53-55.

[3] HUSSAIN K F, ALI S A, MALEK S M. An efficient approach for automatic cloth panel extraction from pattern images [J]. International Journal of Computer Applications, 2014, 98(3): 15-22.

[4] WANG X C, LI K J. Pattern recognition based on fuzzy cluster for recognizing garment style in the photo[C]//9th IEEE International Conference on Computer-Aided Industrial Design and Conceptual Design. Kunming:[s.n], 2008: 250-254.

[5] AN L X, LI W. An integrated approach to fashion flat sketches classification [J]. International Journal of Clothing Science and Technology, 2014, 26(5): 346-366.

[6] ZHANG D, LU G. Review of shape representation and description techniques[J]. Pattern Recognition, 2004, 37(1):1-19.

[7] HOU A L, ZHAO L Q, SHI D C. Garment image retrieval based on multi-features [C]//International Conference on Computer, Mechatronics, Control and Electronic Engineering. Changchun:[s.n.], 2010: 194-197.

[8] GONZALEZ R C, WOODS R E, 阮秋琦, 等. 数字图像处理[M]. 3版. 北京: 电子工业出版社, 2010: 542-543. GONZALEZ R C, WOODS R E, RUN Q Y, et al. Digital Image Processing [M]. 3th ed. Beijing: Publishing House of Electronics Industry, 2010: 542-543.

[9] VAPNIK V N. The Nature of Statistical Learning Theory [M]. New York: Spring, 1995: 13-15.

[10] OTSU N A. Threshold method from gray-level histograms [J]. IEEE Transactions on System Man and Cybernetics, 1979(9): 62-69

[11] CHANG C C, LIN C J. LIBSVM: A library for support vector machines [CP/OL]. 2010-03-11 [2015-11-09]. http://www.csie.ntu.edu.tw/～cjlin/libsvm.

[12] LIU X L, JIA D X, HUI L I, et al. Research on kernel parameter optimization of support vector machine in speaker recognition[J]. Science Technology & Engineering, 2010, 10(7): 1669-1673.

[13] HU M K. Visual pattern recognition by moment invariants [J]. IRE Transactions on Information Theory, 1962, 8: 179-187.

[14] ABDI H, WILLIAMS L J. Principal component analy-sis[J]. Wiley Interdisciplinary Reviews Computational Statistics, 2010, 2(4): 433-459.

[15] HUANG G B, ZHU G Y, SIEW C K. Extreme learning machine: theory and applications [J]. Neurocomputing, 2006, 70(1/3): 489-501.

[16] ZHOU H M, HUANG G B. Elm_kernel [CP/OL]. 2013-09-10 [2015-11-09]. http://www.ntu.edu.sg/home /egbhuang/elm_codes.html.

Clothing style recognition approach using Fourier descriptors and support vector machines

LI Dong1， WAN Xianfu1,2， WANG Jun1, 2
(1.CollegeofTextiles,DonghuaUniversity,Shanghai201620,China; 2.KeyLaboratoryofTextileScience&Technology,MinistryofEducation,DonghuaUniversity,Shanghai201620,China)

In the current clothing style recognition field, clothing contour feature extraction technique was complicated, classification efficiency was low and adaptability was poor. In order to solve these problems and recognize the clothing styles, a novel approach was proposed. In this approach, the contours were extracted from the clothing images, which were taken from the newly created sample database. Then the contour features were described by Fourier descriptors(FD). Finally, the clothing styles were classified by multiclass support vector machines(SVM). The experimental results show that this novel approach can accurately extract the contours of clothing. The recognition effect of the Fourier descriptors is better than the Hu moment invariant and feature fusion (Hu moment invariant and Fourier descriptor). Principal component analysis of FD can′t improve the recognition accuracy, and the classification effect of SVM is better than ELM. This approach can achieve a recognition rate above 95%. In particular, contour features obvious style has a better recognition rate.

clothing style recognition; Fourier descriptor; support vector machine; Hu moment invariant; principal component analysis; extreme learning machine

2016-05-18

2016-11-15

李东(1992—)，男，硕士生。研究方向为服装款式识别。万贤福，通信作者，E-mail:wanxianfu@dhu.edu.cn。

10.13475/j.fzxb.20160504706

TS 941.26

A