表层嵌贴CFRP板加固RC梁的抗弯性能

张智梅,张振波,黄海涛,张振凯,熊浩

(上海大学土木工程系,上海 200444)

表层嵌贴CFRP板加固RC梁的抗弯性能

张智梅,张振波,黄海涛,张振凯,熊浩

(上海大学土木工程系,上海 200444)

利用ABAQUS有限元软件对表层嵌贴碳纤维增强复合材料(carbon fiber reinforced polymer/plastic,CFRP)板加固钢筋混凝土(reiforced concrete,RC)梁的抗弯性能进行非线性有限元分析.通过模拟5根表层嵌贴CFRP板加固RC梁,并将数值模拟结果与试验结果、理论计算结果进行对比,以此验证所建模型的正确性.利用验证后的有限元模型深入分析嵌贴长度、开槽数量、加固方式、纵向配筋率对RC梁抗弯性能的影响.模拟结果表明:嵌贴长度和纵向配筋率对RC梁的抗弯性能影响较大;开槽数量、加固方式对RC梁的抗弯性能影响较小.另外,提出了CFRP板的界限加固量公式.

钢筋混凝土梁;碳纤维增强复合材料板;抗弯性能;表层嵌贴;有限元分析

碳纤维增强复合材料(carbon fiber reinforced polymer/plastic,CFRP)以其抗拉强度高、质量轻、抗疲劳、基本不增加构件截面尺寸等优点,被广泛应用于工程结构的加固[1-2].表层嵌贴(near-surface mounted,NSM)CFRP板加固技术因具有抗剥离能力强、纤维增强复合材料(fiber reinforced polymer/plastic,FRP)利用率高、施工便捷、耐高温等明显优势[2-3],成为国内外广泛研究的课题,并取得了一定的研究成果[3-12].目前,对表层嵌贴CFRP加固钢筋混凝土(reinforced concrete,RC)梁的研究主要集中在试验和理论推导抗弯承载力等方面.本工作采用有限元方法研究表层嵌贴CFRP板加固RC梁的抗弯性能.首先建立试验梁有限元模型,利用ABAQUS软件分析表层嵌贴CFRP板加固RC梁的抗弯性能,并将数值分析结果与试验结果、理论计算结果进行对比分析,验证模型的正确性;然后,利用验证后的有限元模型进一步分析研究相关参数对加固梁抗弯承载力的影响,为加固工程实践提供理论依据;最后,提出加固梁发生界限破坏时CFRP板的加固量公式.

1 试验模型

1.1 钢筋混凝土梁

本工作模拟的试验梁为5根矩形截面简支梁,试验采用四点弯曲加载方式,梁的截面尺寸、跨度及配筋情况如图1所示.利用CFRP板对RC梁进行表层嵌贴加固,板的截面尺寸为16 mm×2 mm,采用双板单槽的方式对RC梁进行表层嵌贴加固.试验梁B500,B1200,B1800 和B2900的加固长度分别为500,1 200,1 800和2 900 mm,其中表层嵌贴均沿跨中对称布置,未加固梁B0为对比梁.

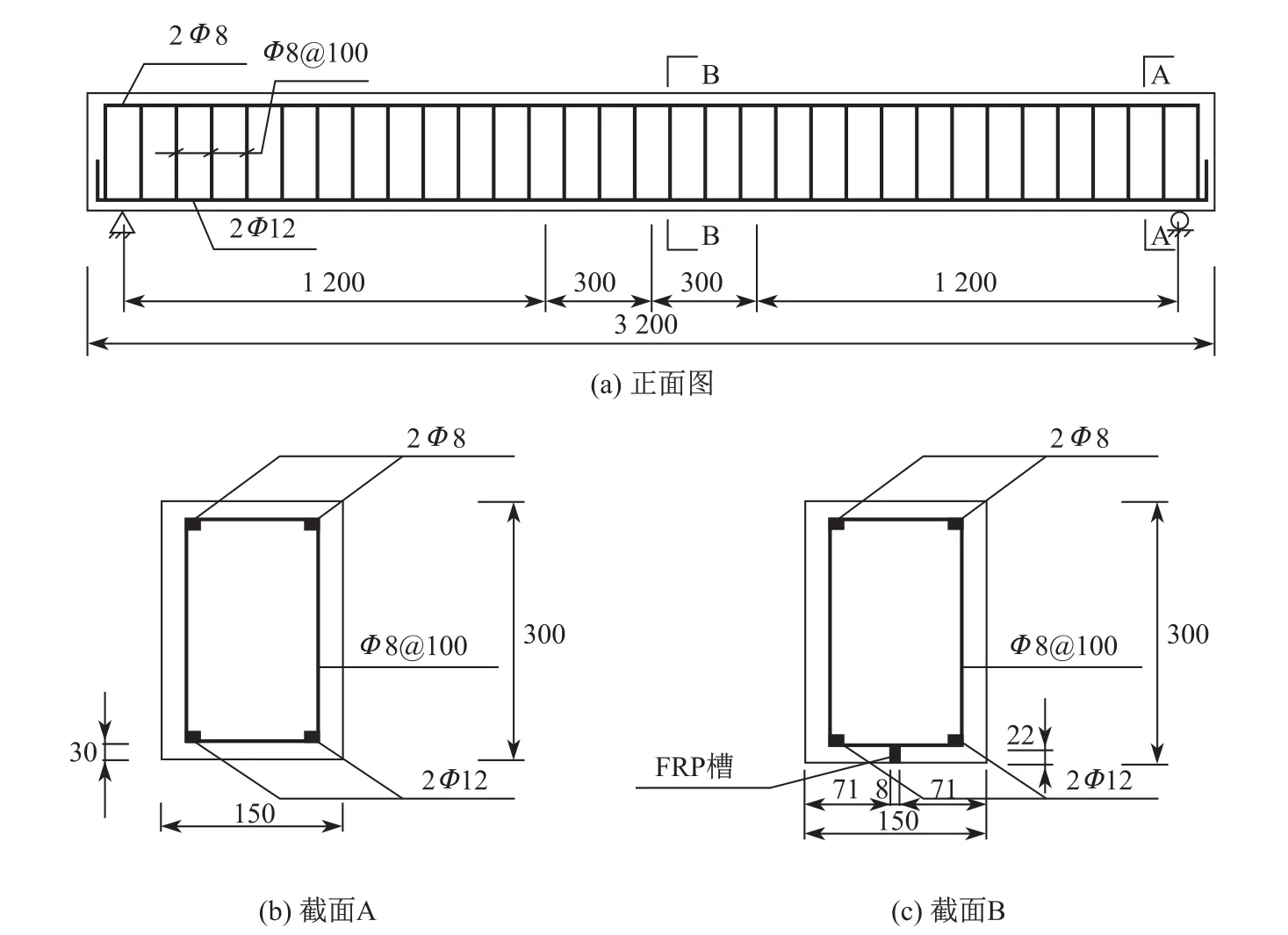
图1 试验梁的截面及配筋(单位:mm)Fig.1 Cross section and reinforcement of test beam(unit:mm)

1.2 材料特性

试验中所用材料的力学性能指标如表1所示.

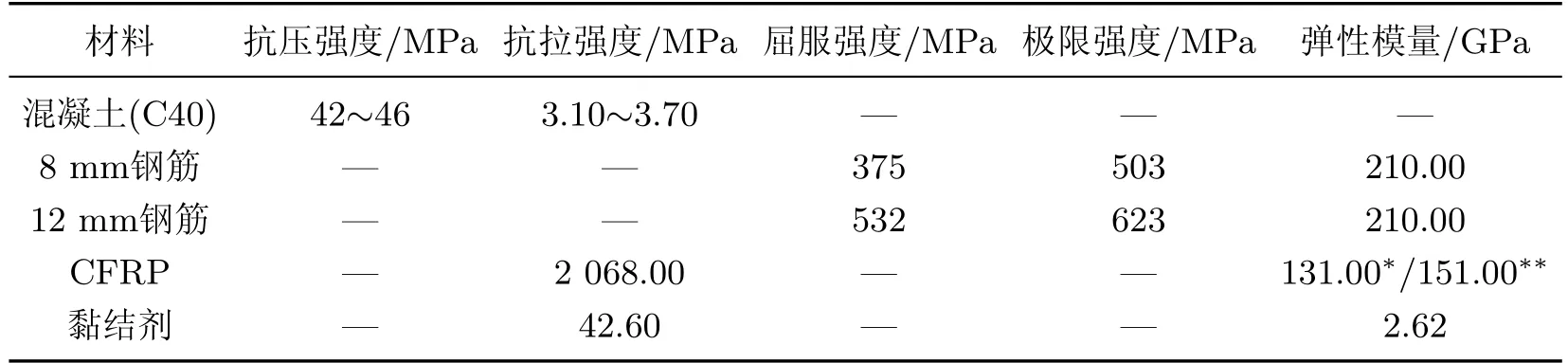
表1 材料的力学性能Table 1 Mechanical properties of materials

2 有限元模型

按照分离式方法建立钢筋混凝土梁的三维分析模型,并利用ABAQUS有限元软件对试验梁进行非线性数值模拟.

模拟时假定钢筋与混凝土之间、黏结剂与混凝土、CFRP板与黏结剂之间均不发生黏结滑移.同时为避免应力集中现象,本模型在支座处和加载点处分别设置2个刚性垫块.混凝土的受拉受压本构关系采用《混凝土结构设计规范》所提供的本构关系曲线,CFRP板、垫块均为理想线弹性材料,钢筋本构为理想弹塑性模型.混凝土、钢筋、CFRP板的材料参数均采用实测值.混凝土、CFRP板、黏结剂、垫块采用C3D8R单元,钢筋采用T3D2单元.

各材料之间的接触条件如下:钢筋与混凝土之间为内置区域约束,垫块与混凝土之间为绑定约束,黏结剂与混凝土之间为绑定约束,CFRP板与黏结剂之间为内置区域约束.根据简支梁的受力特点,在左侧梁端下部钢垫块底部中线处的节点约束5个方向的自由度(位移自由度U1,U2,U3=0,转角自由度UR1,UR2=0),右侧梁端下部钢垫块底部中线处的节点约束4个方向的自由度(位移自由度U2,U3=0,转角自由度UR1,UR2=0).采用位移加载模式,加载量参考试验跨中的破坏挠度.试验梁的有限元模型如图2所示.

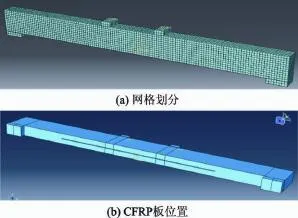
图2 试验梁的有限元模型Fig.2 Finite element models of test beam

3 有限元分析与试验、理论计算结果的对比

3.1 有限元分析与试验观察

为了验证上述建立的有限元模型的可靠性,将通过有限元模拟得到的梁的荷载-跨中挠度曲线与相应的试验结果进行对比分析,结果如图3和表2所示.由于篇幅限制,本工作仅给出试验梁B0,B500,B1200和B1800的荷载-跨中挠度曲线.

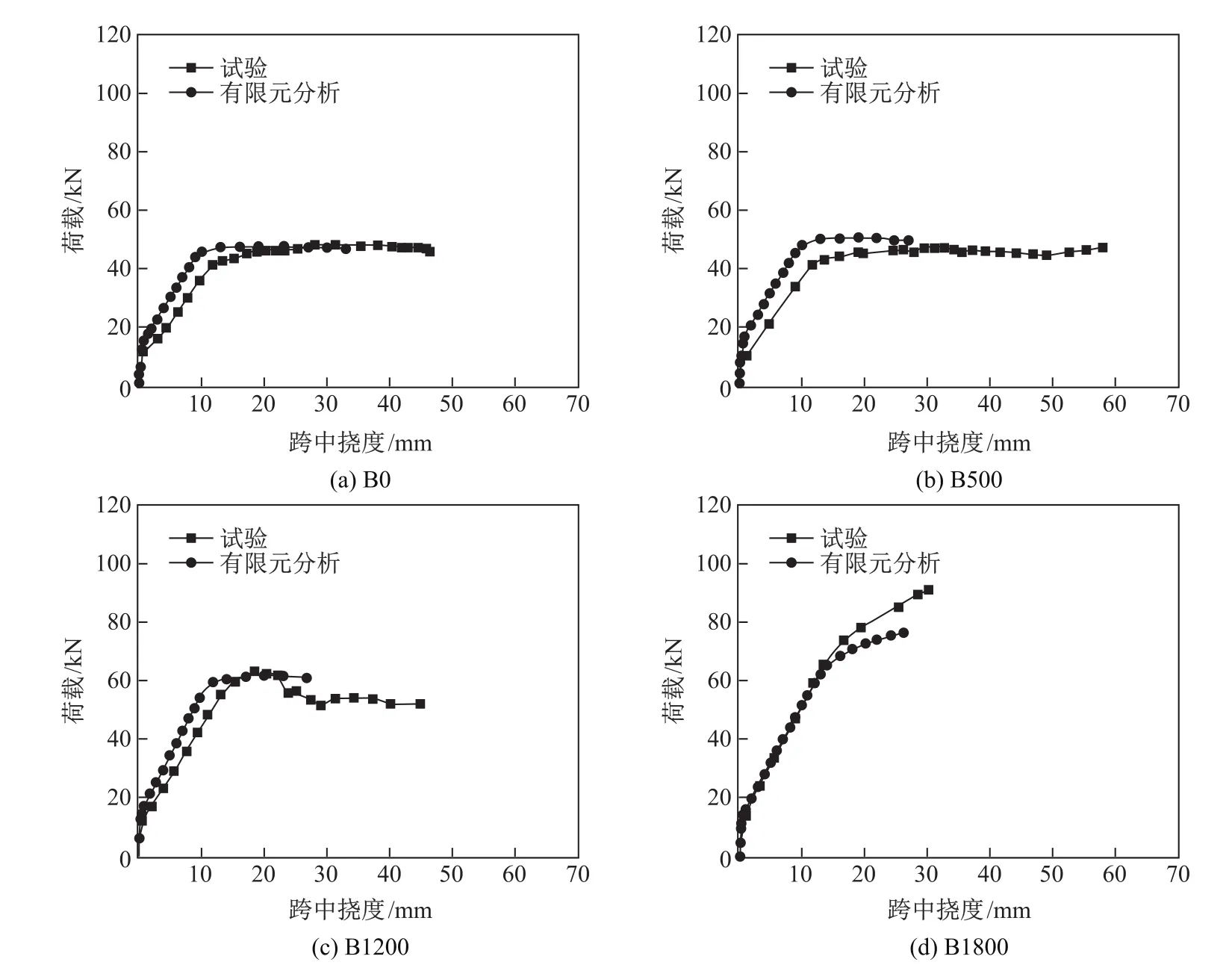
图3 试验与有限元分析得到的荷载-跨中挠度曲线的对比Fig.3 Comparisons of the load-midspan deflection between experiments and finite element analysis

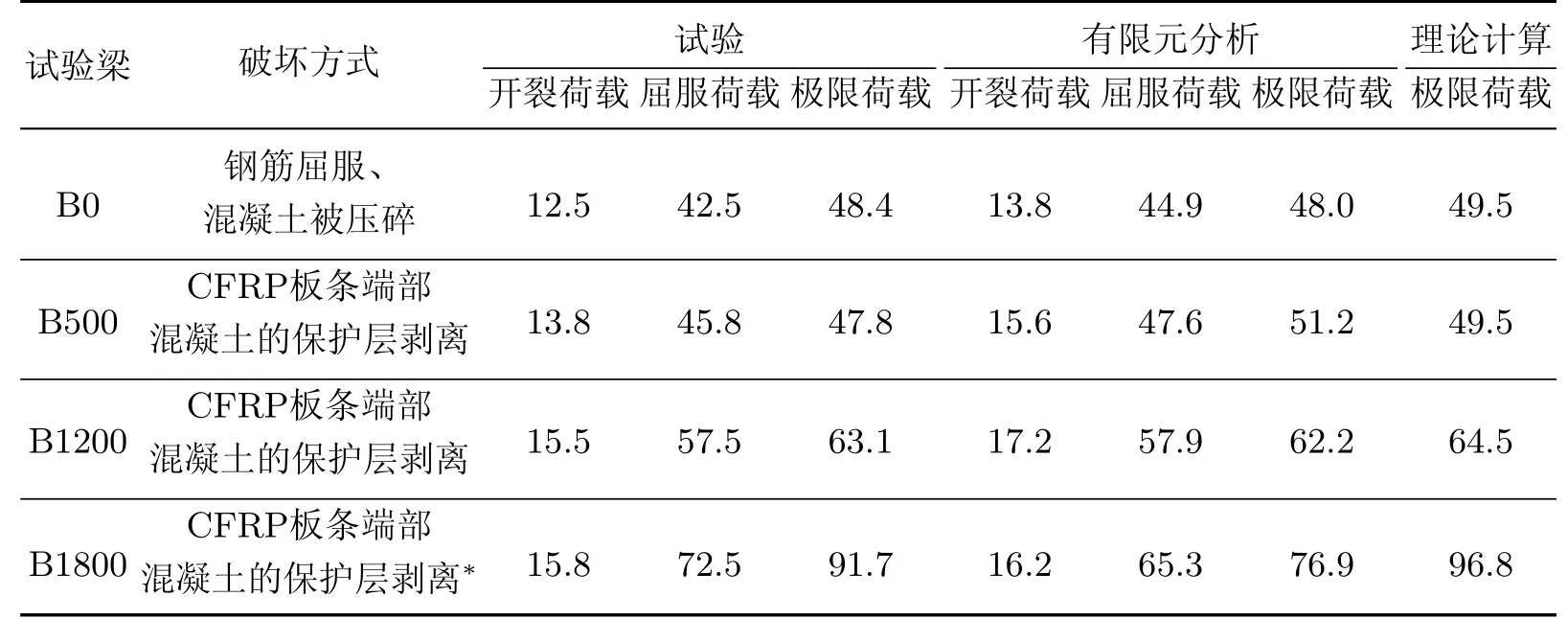
表2 梁弯曲时试验、有限元分析和理论计算结果的比较Table 2 Comparisons of experiments,finite element analysis and theoretical calculation for bending beamskN

由图3可以看出,通过有限元分析和试验分别得到的荷载-跨中挠度曲线,二者整体趋势比较吻合.由表2可以看出,通过有限元分析与试验两种方法分别得到的开裂荷载值的误差均控制在13%以内,屈服荷载值的误差均控制在10%以内,极限荷载值的误差均控制在16%以内.随着表层嵌贴CFRP板长度的增加,数值模拟结果与试验结果越来越吻合,这说明随着表层嵌贴CFRP板长度的增加,CFRP板与黏结材料以及黏结材料与混凝土之间的剥离现象会减弱.图4为加固梁B1800达到极限荷载时,通过有限元模拟得到的裂纹云图和试验观察结果的对比,可以看出有限元模拟得到的裂缝开展情况与试验结果吻合较好.

图4 加固梁B1800达到极限荷载时试验与有限元分析裂缝分布结果的对比Fig.4 Comparison of experiment and finite element analysis for crack pattern of strengthened beam B1800 up to ultimate load

3.2 有限元分析与理论计算

通过有限元分析得到试验梁的破坏形式为钢筋屈服、混凝土被压碎、CFRP未被拉断.根据文献[10]中给出的加固梁的承载力理论计算值(见表2),可知有限元分析与理论计算分别得到的极限荷载之间的最大误差为20%,平均误差为5%,这表明二者吻合较好.

表3为CFRP板嵌贴长度不同时通过理论计算和有限元分析分别得到的RC梁的承载力.在此通过数值拟合得到与嵌贴长度有关的修正系数λ,

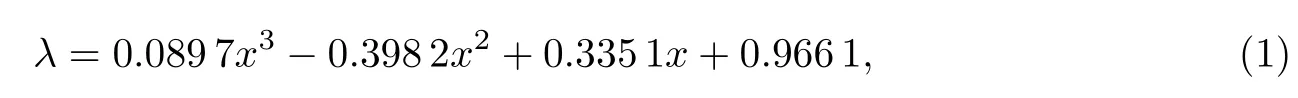
式中,x为嵌贴长度.因为由式(1)得到的承载力(修正值)明显低于理论值,所以有限元模型偏于安全.

表3 CFRP板嵌贴长度不同时RC梁的承载力Table 3 Bearing capacities of RC beams under differrent CFRP lengths

综上分析可知,本工作建立的有限元模型是可靠的,因此可以基于该有限元模型进一步探讨各种因素对表层嵌贴CFRP板加固RC梁抗弯性能的影响.

另外,数值分析结果与试验结果存在一定的偏差,分析其原因主要在于:①在建模过程中,未考虑钢筋与混凝土、黏结剂与混凝土以及CFRP与黏结剂的黏结滑移;②模型中采用的钢筋本构为理想弹塑性模型,即塑性阶段没有考虑应力增长,而实际上钢筋在强化阶段仍有一定的应力增长空间;③模型中采用的混凝土、CFRP和黏结剂等材料的本构关系与实际材料的本构关系之间存在一定差距;④进行数值模拟时,加固梁的边界条件按理想简支处理,而试验中未必能保证梁处于理想简支状态.

4 影响因素分析

影响加固梁抗弯性能的因素较多,本工作主要利用验证后的有限元模型探讨嵌贴长度、开槽数量、加固方式和纵向配筋率对表层嵌贴CFRP板加固RC梁抗弯性能的影响.

4.1 嵌贴长度

本工作对CFRP板嵌贴长度分别为0,500,1 200,1 800,2 900 mm的RC梁进行有限元分析,结果如图5所示.由图5可知,CFRP板的加固长度为500 mm时,加固梁B500与未加固梁B0的跨中挠度-荷载曲线基本重合,可见加固效果不明显;随着CFRP板长度的增加,加固梁的屈服荷载、极限荷载均有所提高,但当加固长度大于1 800 mm时,加固梁承载力的变化较小.这说明存在一个理想的加固长度,超过该值时,CFRP板对加固梁承载力的提高不再有效.因此就本工作所而言,可以将1 800 mm作为理想的加固长度.另外,由图5还可以看出,随着CFRP板嵌贴长度的增加,RC加固梁的延性有所降低.

图5 CFRP板嵌贴长度不同时RC梁荷载-跨中挠度曲线的对比Fig.5 Comparisons of the midspan deflection-load curves for RC beams under different CFRP lengths

4.2 开槽数量

在保持CFRP加固量不变的前提下,对开槽数量分别为1和2的4种RC梁进行有限元分析,结果如图6和表4所示.可以看出,随着开槽数量的增加,RC加固梁的开裂荷载、屈服荷载和极限荷载都有一定程度的增大,其中开裂荷载增大1%～2%,屈服荷载增大0.5%～4.0%,极限荷载增大1%～4%.这表明增加开槽数量,使得RC加固梁的抗弯性能有一定的提高.另外,对比RC梁在不同开槽情况下CFRP的利用率可以看出,随着开槽数量的增加,CFRP的利用率均有不同程度的提高.

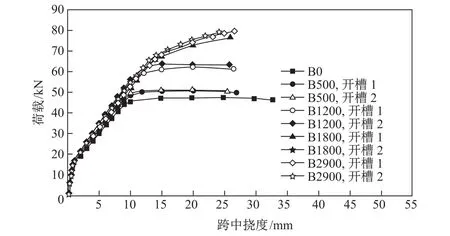
图6 开槽数量不同时RC梁跨中挠度-荷载曲线的对比Fig.6 Comparisons of the midspan deflection-load curves for RC beams under different groove numbers

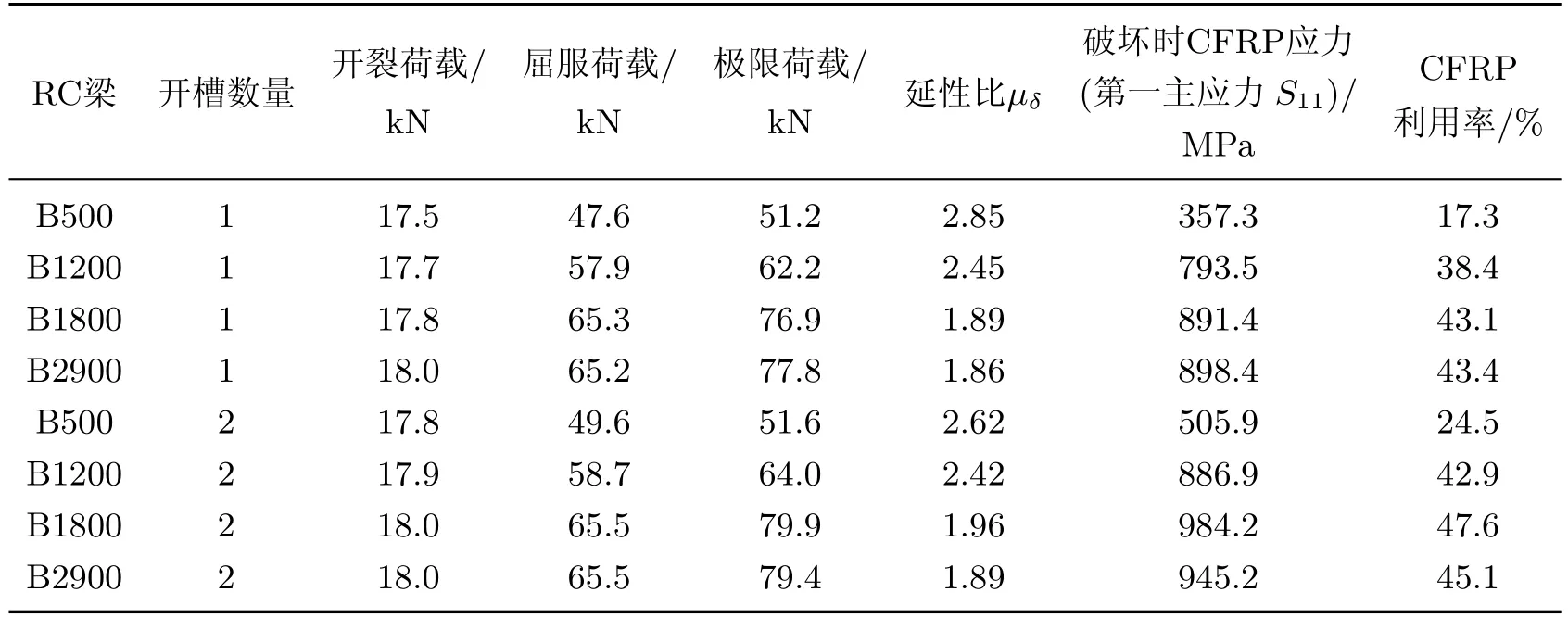
表4 RC梁在开槽数量不同时的有限元分析结果Table 4 Finite element analysis results of RC beams under different groove numbers

4.3 加固方式

考虑到CFRP板表层嵌贴与表层外贴对RC梁抗弯性能的影响不同,本工作采用有限元模拟对比分析了表层外贴与表层嵌贴相同量CFRP板的加固梁,结果如图7所示.由图7可知,由于未考虑CFRP板与RC梁之间的黏结滑移,表层嵌贴与表层外贴情况下的跨中挠度-荷载曲线几乎完全重合.实际上表层外贴的黏结滑移现象比表层嵌贴时更显著,表层嵌贴CFRP板加固RC梁的抗弯性能也更优越.

4.4 纵向配筋率

考虑到纵向受拉筋的配筋率对表层嵌贴CFRP加固RC梁抗弯性能的影响,本工作研究了配筋率不同时RC梁的抗弯性能,其中纵向受拉筋的直径分别为10,12,14 mm.因篇幅限制,本工作仅给出RC梁B500,B1800的跨中挠度-荷载曲线,结果如图8所示.由图8可知,随着纵向配筋率的增大,加固梁的开裂荷载、屈服荷载和极限荷载都增大,这说明提高纵向配筋率,能够较大地提高加固梁的抗弯性能.另外,随着纵向配筋率的增大,加固梁的刚度也明显增大,而延性变差.

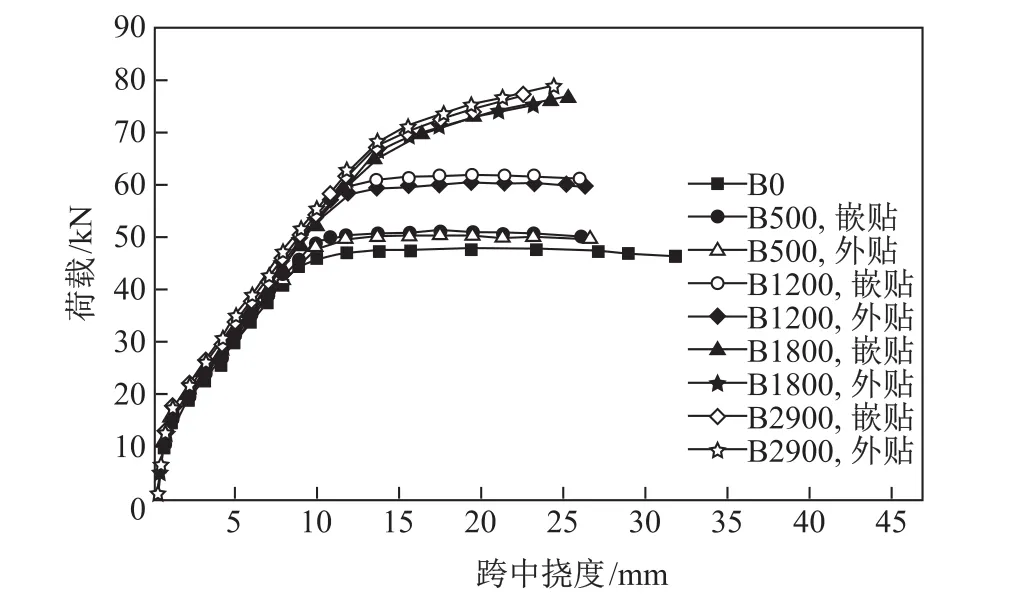
图7 加固方式不同时RC梁跨中挠度-荷载曲线的对比Fig.7 Comparisons of the midspan deflection-load curves for RC beams under different strengthening methods

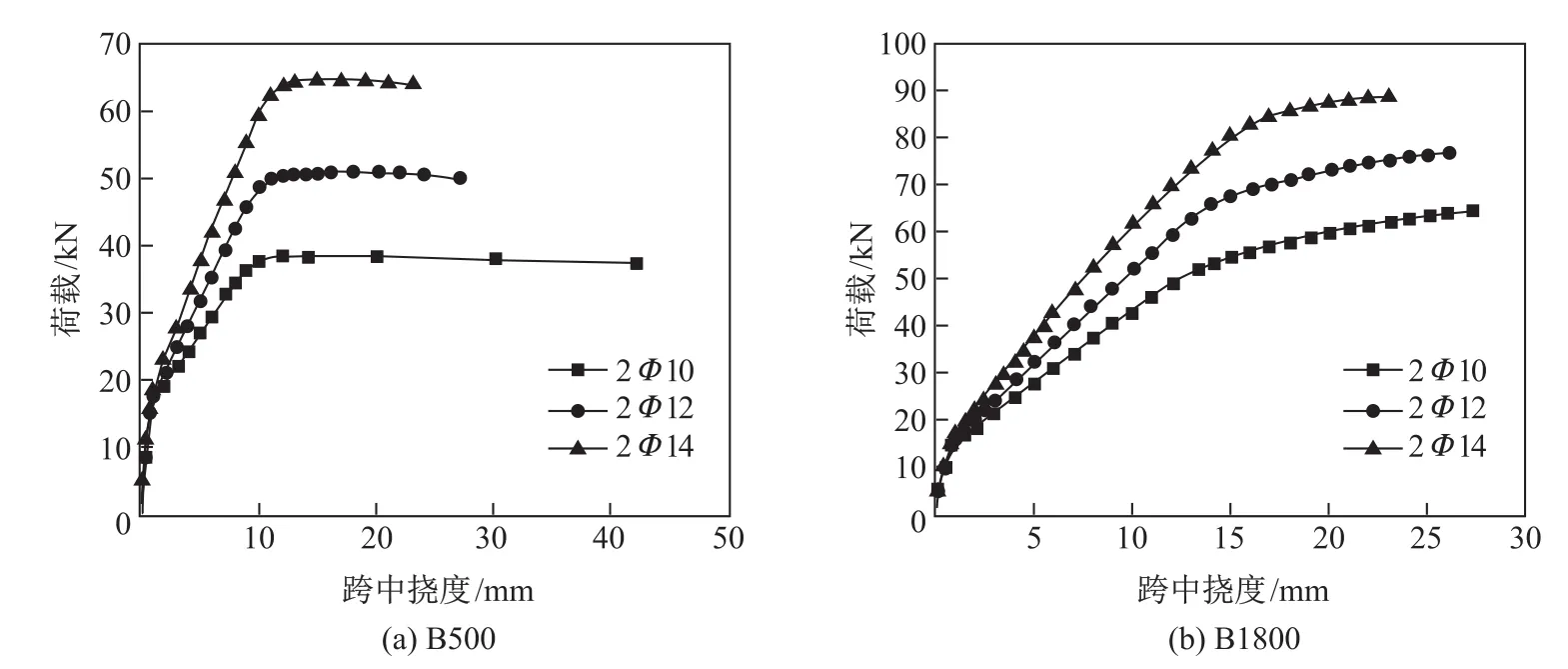
图8 纵向配筋率不同时RC梁跨中挠度-荷载曲线的对比Fig.8 Comparisons of the midspan deflection-load curves for RC beams under different longitudinal reinforcement ratios

5 CFRP板的利用率

提取CFRP板单元最大的第一主应力(一般位于纯弯区域,如跨中位置),用以考察CFRP强度的利用率.CFRP利用率为

式中,σ11为CFRP板最大的第一主应力,ffu为CFRP板的抗拉强度.试验梁的CFRP利用率如表4所示.可以看出,CFRP的利用率随着嵌贴长度的增加而增大.有限元分析表明加固梁的CFRP利用率不足50%,因此合理选择CFRP的加固量至关重要.

在通常情况下,试验梁的破坏形式为钢筋屈服、混凝土被压碎、CFRP板未被拉断.若钢筋屈服后,CFRP被拉断与混凝土被压碎同时发生,加固梁发生临界破坏,则根据计算简图9可得

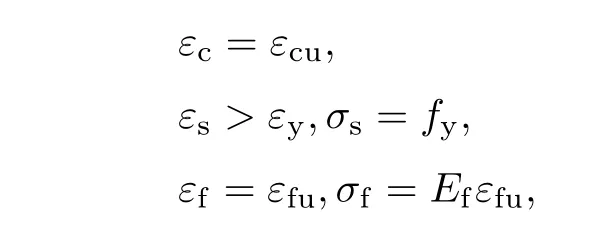
式中,εc为混凝土压应变,εcu为混凝土极限压应变,εs为钢筋拉应变,εy为钢筋极限拉应变, σs为钢筋拉应力,fy为钢筋屈服强度,εf为CFRP拉应变,εfu为CFRP极限拉应变,σf为CFRP拉应力,Ef为CFRP的弹性模量.

图9表层嵌贴CFRP板加固RC梁截面及抗弯承载力计算简图

Fig.9 NSM CFRP-strengthened RC beams section and calculation diagram for the flexural bearing capacity

根据平截面假定和无滑移假定,可得

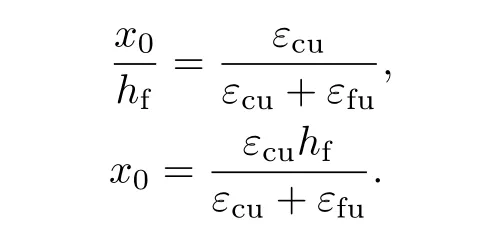
混凝土合力Cc=fcbx,根据《混凝土结构设计规范》(GB 50010—2013)可知,x=0.8x0.

主筋及CFRP板合力为

根据平衡方程Cc=T,可求得加固梁发生临界破坏时CFRP板的加固量为

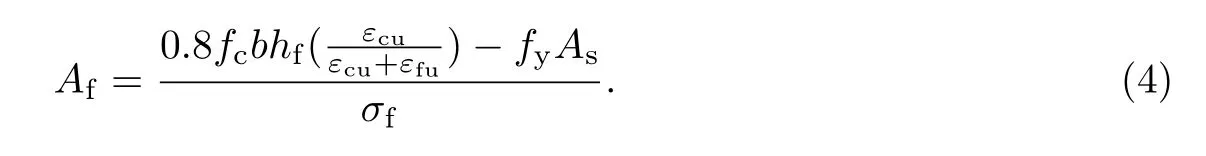
CFRP板的加固量Af是在通常情况下的基础上求得的,若当嵌贴长度不确定时,如何选择CFRP板的加固量有待进一步研究.

6 结论

本工作利用ABAQUS有限元软件深入讨论了嵌贴长度、开槽数量、加固方式和纵向配筋率对表层嵌贴CFRP加固RC梁抗弯性能的影响,主要得到以下结论.

(1)加固梁的抗弯性能主要体现在抗弯承载力、刚度、延性、CFRP利用率等方面,其中嵌贴长度和纵向配筋率对RC梁的抗弯性能影响较大,而开槽数量、加固方式对RC梁的抗弯性能影响较小.

(2)随着CFRP板嵌贴长度的增加,RC梁的开裂荷载、屈服荷载和极限荷载均增大, CFRP的利用率提高.当嵌贴长度大于1 800 mm时,嵌贴长度的增加对CFRP利用率的提高效果不明显,对抗弯性能影响较小.因此,可将1 800 mm作为嵌贴CFRP板的理想长度.

(3)随着开槽数量的增加,CFRP的利用率提高.

(4)表层外贴的黏结滑移现象比表层嵌贴时更明显,因此相较于表层外贴,表层嵌贴CFRP加固RC梁的抗弯性能更优.

(5)随着纵向配筋率的增大,CFRP的利用率下降明显,因此应该合理选择纵向配筋率与CFRP的加固量,充分利用钢筋和CFRP板的抗弯性能.

(6)提出了承载力修正系数λ,利用该修正系数计算得到的加固梁的承载力偏于安全,可应用于工程实际.

[1]李荣,滕锦光,岳清瑞.FRP材料加固混凝土结构应用的新领域——嵌入式(NSM)加固法[J].工业建筑,2004,34(4):5-10.

[2]张智梅,考书姣,白世烨.CFRP布加固钢筋混凝土梁的抗弯性能研究[J].结构工程师,2012,28(4): 139-143.

[3]孙志洋,张智梅,刘涛.内嵌CFRP板加固已损伤RC梁抗弯性能的试验研究[J].四川建筑科学研究,2013,39(4):112-116.

[4]贺学军,周朝阳,徐玲.内嵌CFRP板条加固混凝土梁的抗弯性能试验研究[J].土木工程学报, 2008,41(12):14-20.

[5]陆新征,滕锦光,叶列平,等.FRP加固混凝土梁受弯剥离破坏的有限元分析[J].工程力学,2006, 23(6):85-93.

[6]周朝阳,向传家,贺学军.内嵌FRP加固钢筋混凝土梁的受弯承载力分析[J].建筑结构,2006, 36(12):19-21.

[7]梁金福,燕柳斌,赵君君,等.CFRP板条嵌入式加固钢筋混凝土梁抗弯性能试验研究[J].工业建筑, 2009,39(2):100-102.

[8]曾宪桃,成香莉,高保彬.内嵌碳纤维增强塑料板条抗弯加固混凝土梁试验研究[J].工程力学,2008, 25(12):106-113.

[9]DE LORENZIS L.Anchorage length of near-surface mounted fiber-reinforced polymer rods for concrete strengthening analytical modeling[J].ACI Structure Journal,2004,101(2):375-386.

[10]TENG J G,LORENZIS L D,WANG B,et al.Debonding failures of RC beams strengthened with near-surface mounted CFRP strips[J].Journal of Composites for Construction,2006,10(2): 92-105.

[11]DE LORENZIS L,TENG J G.Near-surface mounted FRP reinforcement:an emerging technique for strengthening structures[J].Composites Part B:Engineering,2007,38:119-143.

[12]NOVIDIS D,PANTAZOPOULOU S J,TENTOLOURIS E.Experimental study of bond of NSM-FRP reinforcement[J].Construction and Building Materials,2007,21(8):1760-1770.本文彩色版可登陆本刊网站查询:http://www.journal.shu.edu.cn

Flexural behavior of RC beams strengthened with near surface mounted CFRP strips

ZHANG Zhimei,ZHANG Zhenbo,HUANG Haitao, ZHANG Zhenkai,XIONG Hao
(Department of Civil Engineering,Shanghai University,Shanghai 200444,China)

This paper uses the finite element software ABAQUS for nonlinear finite element analysis of the flexural behavior of reinforced concrete(RC)beams with near-surface mounted(NSM)carbon fiber reinforced polymer/plastic(CFRP)strips.Through simulation of 5 beams with NSM CFRP strips from the test,the experimental and theoretical results were compared to verify accuracy of the model.Using the verified finite element model,the influence of factors were analyzed such as FRP length,groove number,reinforcement method and longitudinal reinforcement ratio on the flexural behavior of RC beams. The results show that the CFRP length and longitudinal reinforcement ratio have a larger impact on the flexural behavior of the RC beams,while the impacts of groove number and reinforcement method are limited.This paper also proposes a boundary reinforcement quantity formula for CFRP strips.

reinforced concrete(RC)beam;carbon fiber reinforced polymer/plastic (CFRP)strip;flexural behavior;near-surface mounted(NSM);finite element analysis

TU 375.1

A

1007-2861(2017)02-0298-10

10.3969/j.issn.1007-2861.2015.02.002

2015-04-03

张智梅(1972—),女,副教授,博士,研究方向为混凝土结构加固.E-mail:zhangzhimei@staff.shu.edu.cn