Dirac孤子族的三可积耦合及其双Hamiltonian结构

李倩,夏铁成

(1.上海大学理学院,上海 200444;

2.郑州航空工业管理学院理学院,郑州 450005)

Dirac孤子族的三可积耦合及其双Hamiltonian结构

李倩1,2,夏铁成1

(1.上海大学理学院,上海 200444;

2.郑州航空工业管理学院理学院,郑州 450005)

基于扩大的零曲率方程和矩阵李代数的半直和,得到了Dirac孤子族的三可积耦合,并借助变分恒等式得到了三可积耦合的双Hamiltonian结构.

Dirac孤子族;三可积耦合;双Hamiltonian结构

众所周知,可积耦合是孤子理论中有趣而重要的课题[1-3].研究可积耦合不仅可以概括对称问题,而且为可积系统的完全分类提供了线索,甚至可以显现出可积方程所拥有的数学结构.自从可积耦合的定义[4]被提出后,方程族可积耦合得到广泛关注,并出现了很多建立方程组可积耦合的方法,如扩大谱问题、李代数的半直和、新的李代数等[5-20].关于可积耦合的研究甚至推广到了超可积系统[18-20].2012年,Ma[21]用块型矩阵李代数建立了方程族的双可积耦合,之后又进一步将双可积耦合推广到三可积耦合[22].

对于给定的可积系统

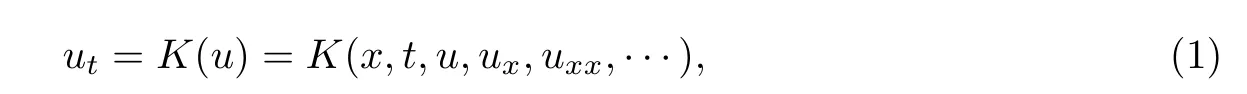
式中,u为独立变量构成的列向量.可积系统(1)的三可积耦合指的是扩大的三角形可积系统:

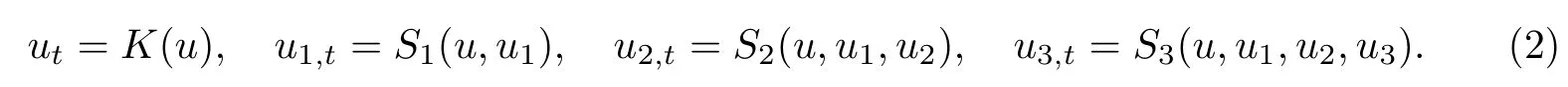
如果S1(u,u1),S2(u,u1,u2)和S3(u,u1,u2,u3)中至少有一个关于任何新的独立变量u1,u2,u3是非线性的,则称这个系统是非线性可积耦合的.

为了建立三可积耦合,需要一系列三角形4×4的分块矩阵M(A1,A2,A3,A4),其中Ai(1≤i≤4)是同阶的方阵.引入一系列具有半直和分解的矩阵李代数：

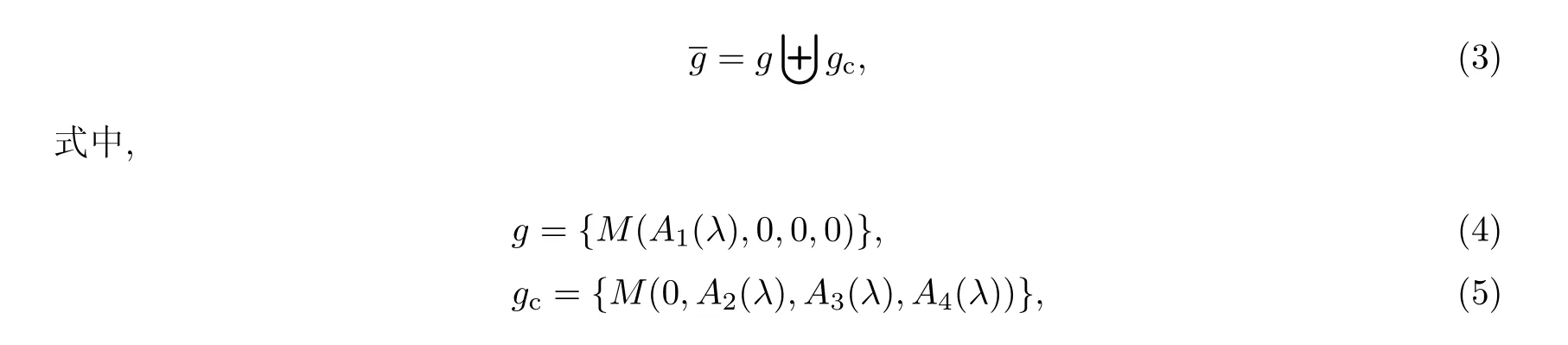
其中Ai(λ)(i=1,2,3,4)为λ的罗朗级数,则其必为非半单的.显然,gc是的一个非平凡理想.

上述所提出的李代数为产生非线性三可积耦合提供了一组基,因为交换算子[A2,B2] 和[A3,B3]在对应的三可积耦合中能够产生非线性项,而其余现有的李代数产生线性可积耦合,其中子块A1对应原始的可积系统,子块A2,A3和A4用来生成辅助向量域S1,S2和S3.

本工作的主要目的是基于文献[23]中的方法建立Dirac族的三可积耦合.选取其中一个分块矩阵:

式中,α,β和µ是3个任意给定的常数.进一步地,希望获得对应三可积耦合的双Hamiltonian结构.

1 Dirac族

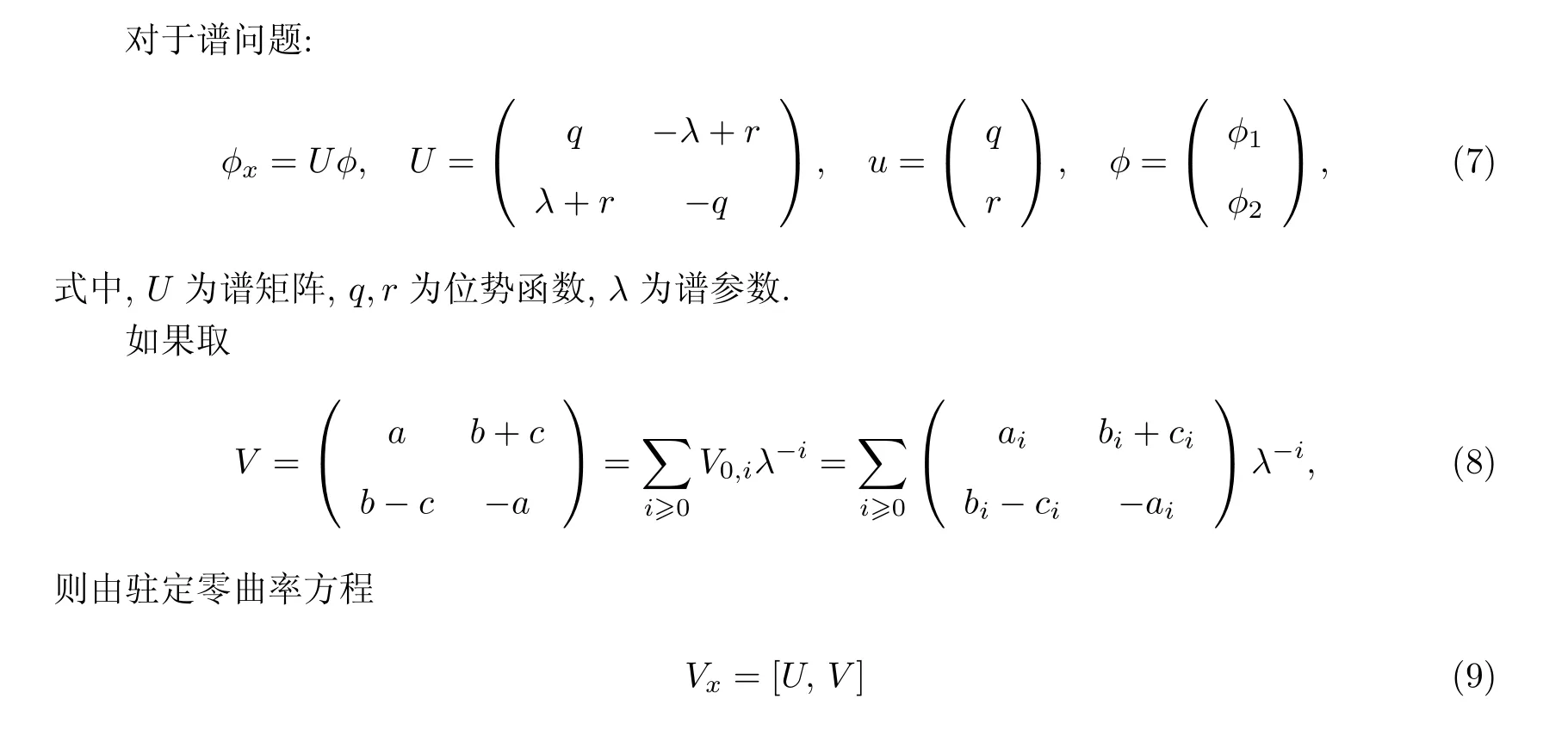
2 Dirac族的三可积耦合

基于特殊的非半单李代数,选取如下扩大的谱矩阵:

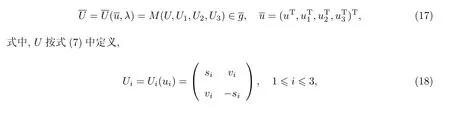
其中si,vi是新的独立变量.为了求解扩大的零曲率方程

当m≥2时,由式(31)可以得出Dirac方程族的非线性三可积耦合.

3 Hamiltonian结构

应用变分恒等式(23)建立对应三可积耦合的Hamiltonian结构:

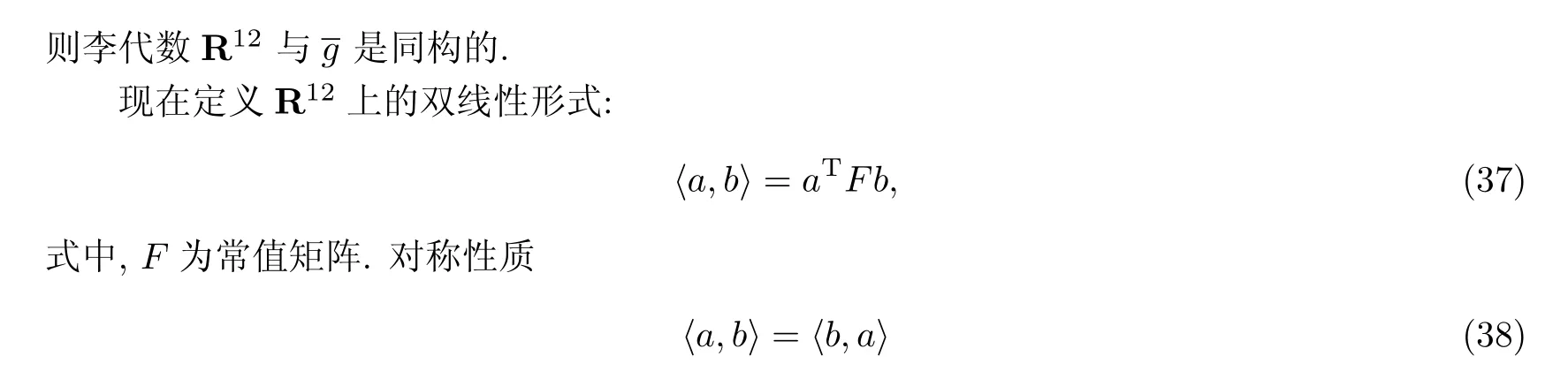
要求FT=F.在对称条件下,不变性质〈a,[b,c]〉=〈[a,b],c〉等价于要求F(R(b))T=−R(b)F, b∈R12.具有任意常数b的矩阵方程产生矩阵F的线性系统,求解对应的系统可以得到

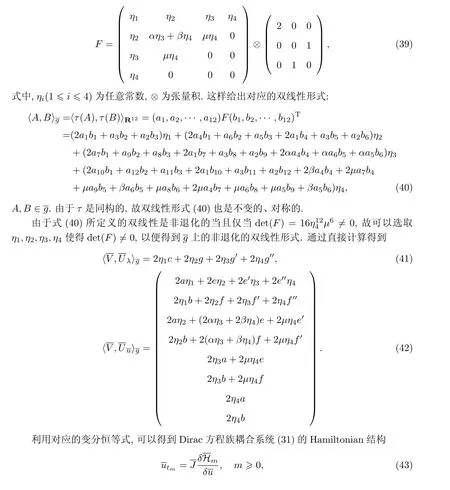
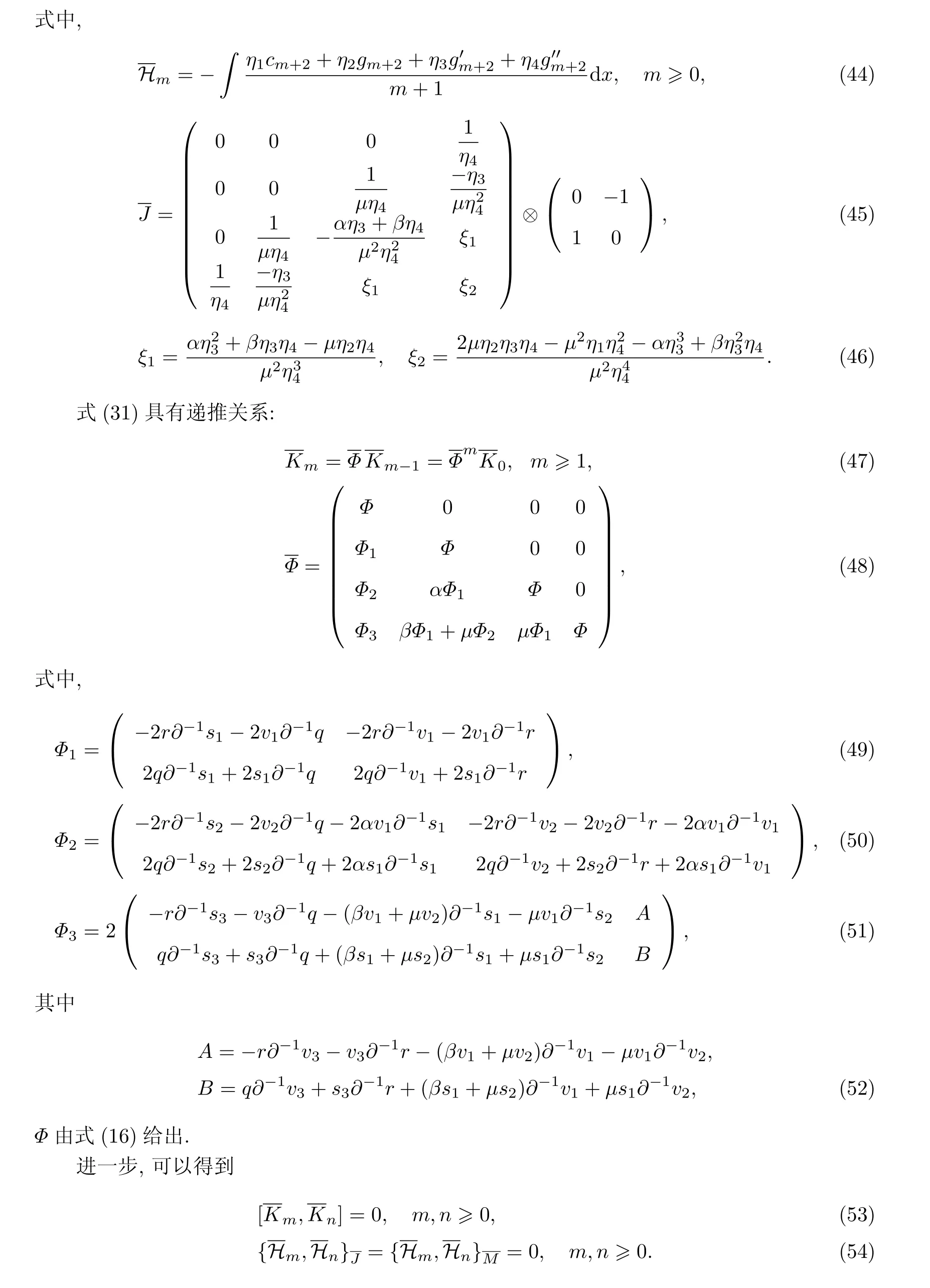
[1]ABLOWITZ M,LADIK J F.Nonlinear differential-difference equation[J].Journal of Mathematical Physics,1975,16(3):598-603.

[2]TU G Z.A trace identity and its applications to the theory of discrete integrable systems[J]. Journal of Physics A:Mathematical and General,1990,23(17):3903-3922.

[3]OHTA Y,HIROTA R.A discrete KdV equation and its Casorati determinant solution[J].Journal of the Physical Society of Japan,1991,60(6):2095.

[4]MA W X,FUCHSSTEINER B.Integrable theory of the perturbation equations[J].Chaos, Solitons&Fractals,1996,7(8):1227-1250.

[5]MA W X,XU X X,ZHANG Y F.Semi-direct sums of Lie algebras and continuous integrable couplings[J].Physics Letter A,2006,351(3):125-130.

[6]MA W X.Enlarging spectral problems to construct integrable couplings of soliton equations[J]. Physics Letters A,2003,316(2):72-76.

[7]ZHANG Y F.A generalized multi-component Glachette-Johnson(GJ)hierarchy and its integrable coupling system[J].Chaos,Solitons&Fractals,2004,21(2):305-310.

[8]GUO F K,ZHANG Y F.A new loop algebra and a corresponding integrable hierarchy,as well as its integrable coupling[J].Journal of Mathematical Physics,2003,44(12):5793-5803.

[9]XIA T C,YOU F C.Generalized multi-component TC hierarchy and its multi-component integrable coupling system[J].Communications in Theoretical Physics,2005,44(5):793-798.

[10]MA W X.Nonlinear continuous integrable Hamiltonian couplings[J].Applied Mathematics and Computation,2011,217(17):7238-7244.

[11]ZHANG Y F,TAM H.Four Lie algebras associated with R6and their applications[J].Journal of Mathematical Physics,2010,DOI:10.1063/1.3489126.

[12]MA W X,ZHU Z N.Constructing nonlinear discrete integrable Hamiltonian couplings[J].Computers&Mathematics with Applications,2010,60(19):2601-2608.

[13]YU F J.A real nonlinear integrable couplings of continuous soliton hierarchy and its Hamiltonian structure[J].Physics Letters A,2011,375(13):1504-1509.

[14]ZHANG Y F.Lie algebras for constructing nonlinear integrable couplings[J].Communications in Theoretical Physics,2011,56(5):805-812.

[15]ZHANG Y F,FAN E G.Coupling integrable couplings and bi-Hamiltonian structure associated with the Boiti-Pempinelli-Tu hierarchy[J].Journal of Mathematical Physics,2010,DOI: 10.1063/1.3462736.

[16]GUO F K,ZHANG Y F.The quadratic-form identity for constructing the Hamiltonian structure of integrable systems[J].Journal of Physics A:Mathematical and General,2005,38:8537-8548.

[17]ZHANG Y F,ZHANG H Q.A direct method for integrable couplings of TD hierarchy[J].Journal of Mathematical Physics,2002,43(1):466-472.

[18]YOU F C.Nonlinear super integrable couplings of super Dirac hierarchy and its super Hamiltonian structures[J].Communications in Theoretical Physics,2012,57(6):961-966.

[19]MA W X,HE J S,QIN Z Y.A super trace identity and its applications to super integrable systems[J].Journal of Mathematical Physics,2008,DOI:10.1063/1.2897036.

[20]YOU F C.Nonlinear super integrable Hamiltonian couplings[J].Journal of Mathematical Physics,2011,DOI:10.1063/1.3669484.

[21]MA W X.Loop algebras and bi-integrable couplings[J].Chinese Annals of Mathematics B, 2012,33(2):207-224.

[22]MENG J,MA W X.Hamiltonian tri-integrable couplings of the AKNS hierarchy[J].Communications in Theoretical Physics,2013,59(4):385-392.

[23]MA W X.Variational identities and applications to Hamiltonian structures of soliton equations[J].Nonlinear Analysis,2009,71(12):1716-1726.

[24]OLVER P J.Applications of Lie groups to differential equations[M].New York:Springer-Verlag, 1986.

Tri-integrable couplings of Dirac hierarchy and its bi-Hamiltonian structure

LI Qian1,2,XIA Tiecheng1
(1.College of Sciences,Shanghai University,Shanghai 200444,China; 2.College of Sciences,Zhengzhou University of Aeronautics,Zhengzhou 450005,China)

Tri-integrable couplings of Dirac hierarchy are obtained based on the enlarged zero curvature equation from semi-direct sums of Lie algebras.Its bi-Hamiltonian structures are then established with variational identity.

Dirac hierarchy;tri-integrable couplings;bi-Hamiltonian structure

O 175.2

A

1007-2861(2017)02-0257-10

10.3969/j.issn.1007-2861.2015.04.022

2015-10-26

国家自然科学基金资助项目(11271008,61640315);河南省高等学校重点科研资助项目(17A120006)

夏铁成(1960—),男,教授,博士生导师,研究方向为孤子与可积系统.E-mail:xiatc@shu.edu.cn