三电平有源电力滤波器死区效应分析与补偿
黄海宏,江念涛,黄楠楠,王海欣
(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)
0 引言
随着现代社会的飞速发展,电能质量问题日益凸显。作为改善电能质量最有效的治理方式,有源电力滤波器(APF)的市场需求越来越大。由于APF主电路的开关器件不是理想器件,为防止同一桥臂功率管直通,必须在互补的2个驱动信号中设置一段死区时间,以保证互补开关管的先关断后导通。在死区时间内,输出波形不受逻辑信号的控制,同时在较高的开关频率下,APF的补偿性能[1-5]会严重降低。死区效应[6-7]使得脉冲宽度调制(PWM)信号不能实时准确地施加到开关管的控制端,进而导致APF输出电流与期望值偏差较大。偏差中含有大量需要补偿的谐波成分,这导致APF输出的谐波电流的幅值与相位都有很大偏差,从而影响谐波补偿效果。
消除死区的方法有很多,如死区解耦控制方法、基于电流预测的死区补偿方法及基于单周控制的死区补偿方法[7-10]。 文献[8-9]提出基于电流预测的死区补偿方法,但由于高频噪声及电磁干扰的存在,增加了对电流极性的判断难度。若电流检测不准或滞后时间过长则会导致补偿不准,进而可能会使死区效应的影响加重。尤其对于具有较强电磁干扰的三电平APF而言,其补偿效应更不佳。现有文献中对死区效应补偿控制的研究比较多,文献[10]提出一种不直接判断电流极性的新方法,该方法根据谐振控制器锁相环的网侧电压观测值间接实现对电流方向的准确判断,进而实现死区补偿,但由于三电平系统中存在严重的电磁干扰同样会对网侧电压采样造成影响,补偿效果仍不佳。文献[11]提出一种新型的自适应死区补偿控制方法,该控制方法无需检测电流极性,在同步旋转坐标系下,通过PI控制器调节扰动观测器观测出的q轴扰动电压,获得死区补偿时间,进而基于空间矢量脉宽调制(SVPWM)实现死区补偿。但该控制策略建立了自适应观测器,系统结构复杂度变高,加大了控制难度,且三电平SVPWM有27个矢量,控制上会更加复杂。
为此,本文深度研究了死区效应对APF电流跟踪的影响。从三电平APF的状态方程出发,推导出电流跟踪误差与死区时间的数学关系,同时结合死区效应产生原理,阐释了死区时间会导致电流跟踪误差增大的原因。在此基础上,提出了PI与重复控制[12-16]相结合的死区补偿方法,该方法引入超前矫正环节对死区进行补偿,在保证补偿前系统具有快速性能的同时,大幅降低了死区效应给APF带来的影响。
1 死区效应分析及补偿控制
本文基于LCL三电平APF的拓扑对死区效应开展讨论分析,结合开关状态方程与死区效应原理图,推导出由于死区带来的电流跟踪误差与死区时间之间的代数关系。图1给出了三电平APF等效开关电路图。
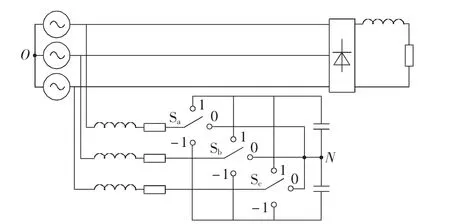
图1 三电平APF等效开关电路图Fig.1 Equivalent circuit schematic diagram of three-level APF
1.1 死区时间影响分析
根据图1所示的三电平APF等效开关电路,以单电感滤波为例进行讨论,定义开关函数如下:
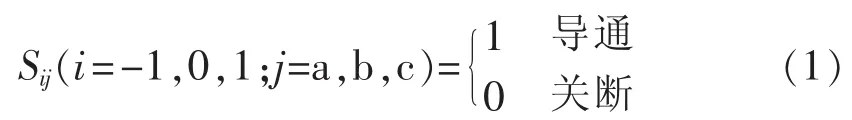
设节点N与O间的电压为uNO,根据三电平APF数学模型得到a相的开关状态方程如下所示(为方便分析,忽略线路等效阻抗)。
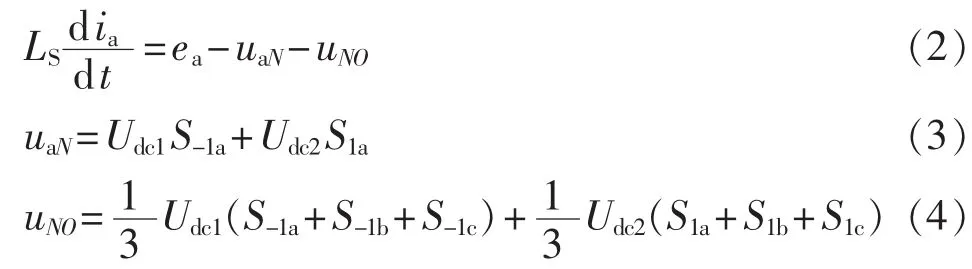
其中,LS为APF输出侧滤波电感;ia为APF输出侧a相电流;ea为网侧a相电压;uaN为APF输出侧a相对直流侧中点电位的电压;Udc1为直流侧正极对中点电位的电压;Udc2为直流侧中点电位对负极的电压。
图2给出了死区效应原理图。定义流入APF的电流方向为正,i>0时只考虑输出电平在1电平与0电平之间切换的阶段,故只给出a相1、2管的驱动信号G1和G2;i<0时只考虑输出电平在-1电平与0电平之间切换的阶段,故只给出a相3、4管的驱动信号G3和G4。从图中可明显看出,死区时间的加入引起了实际电流跟踪误差变大。
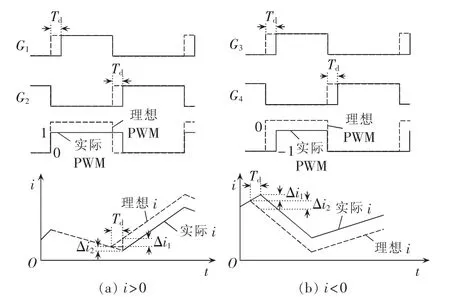
图2 死区生成原理Fig.2 Dead time generation principle
i>0时,不考虑直流侧上下电容电压的偏差,且认为这个过程中其他两相开关状态及电网电压不变。
当S1a=0时,有:
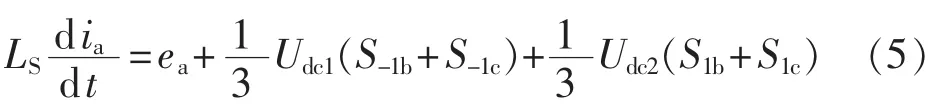
当S1a=1时,有:
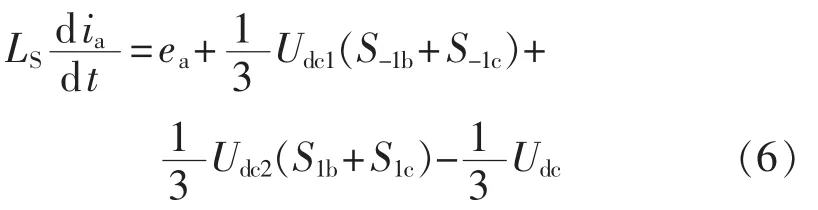
其中,Udc为直流侧电压。
Td期间,a相1、2管的驱动均为低电平,电流经1、2管的反并联二极管续流使PWM输出为高电平。加入死区前,若G1为高电平,则PWM输出与G1一致为高电平;若G1为低电平,在Td阶段开关函数值由加入死区前0变成加入死区后1,故有PWM输出比G1多Td时长的1电平。根据死区原理图可得出实际电流与理论电流之间的偏差,推导如下。
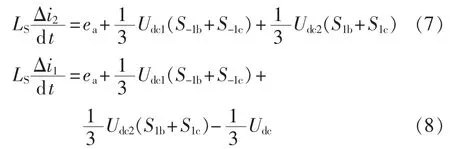
由式(8)减去式(7)得:
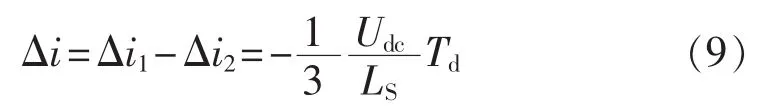
综上,i>0时,加入死区后,实际电流输出值减小,即电流幅值减小。
i<0时,Td期间,a相3、4管驱动均为低电平,电流经3、4管反并联二极管续流使PWM输出为-1电平。加入死区前,若G3为高电平,则PWM输出为0电平;若G3为低电平,而PWM输出为-1电平,故有PWM输出比G3多Td时长的-1电平。同理可得i<0时的实际电流与理想电流之间的偏差:

同理可分析死区时间Td对其他两相PWM输出脉宽的变化,同样可推导得出与式(9)、(10)相同的结果。
综上所述,由于APF正常工作时,直流电压是近似不变的,故电流跟踪误差与死区时间成正比。死区时间越大,电流跟踪误差就越大;死区时间越小,电流跟踪误差就越小。
1.2 死区补偿控制
根据上述分析可知,死区效应加大了电流跟踪误差,从而使得网侧电流畸变严重,补偿效果不佳。本文从电流控制设计角度出发对死区效应进行补偿控制。图3给出了未加死区补偿控制时的电流环运算模型。 图中,i*为指定电流;Kp为比例系数;ui(s)为输入电流;uc(s)为 LCL滤波器的电容电压;L1为网侧电感;L2为桥臂侧电感;i1(s)为网侧电感电流;i2(s)为桥臂侧电感电流;ic(s)为LCL滤波器的电容电流;R和C分别为LCL滤波器的电阻和电容;P(s)为被控对象。
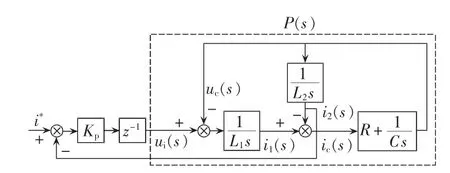
图3 电流环运算模型Fig.3 Operational model of current loop
上述电流环模型并没有考虑死区效应这一干扰信号对电流环控制带来的影响,因此采用常规控制必然不能达到很好的补偿效果。由于死区是按开关频率周期性引入的,因此死区效应可以视作由以开关周期为单位的周期性扰动信号带来的,可以采用PI与重复控制相结合的电流跟踪方式加以补偿。这种死区补偿方式在保证系统具有原来系统的快速响应性的同时,具有较好的稳态性能。
图4给出了电流环控制(PI与重复控制相结合)的运算原理图。重复控制可以视作为积分器和基频整数倍次谐振器的叠加,故重复控制理论上可以无静差跟踪周期信号。其中,A(z-1)的设计是关键环节。
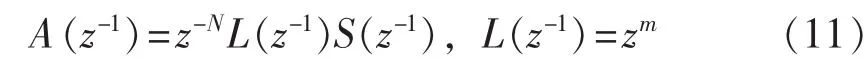
其中,L(z-1)为有效补偿死区效应的核心环节;S(z-1)为补偿环节。为了避免LCL在谐振频率处有较大的开环增益会引起谐振现象,S(z-1)采用数字低通滤波器。由于本系统LCL谐振频率为2.65 kHz,为了保证APF装置对40次谐波的有效补偿,选取滤波器截止频率fc=2.5 kHz,其可保证一定补偿带宽的同时,又能对LCL滤波带来的谐振峰进行有效衰减。

根据图4得到误差传递函数F(z-1),控制对象用P(z-1)表示。
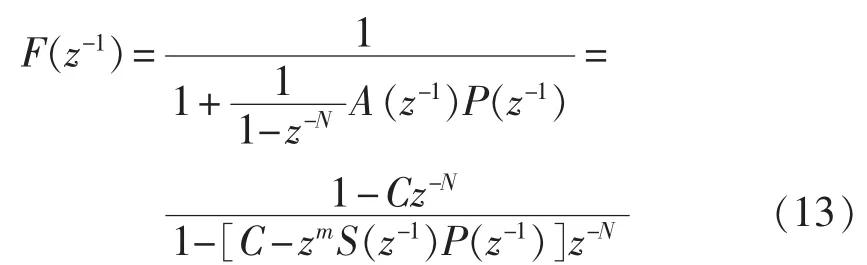
相应的频率函数为:
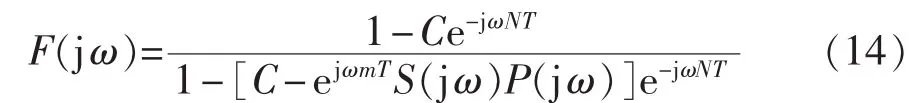
考虑死区带来的干扰主要是3、5、7次等低频谐波,其角频率可以表示为N1倍的工频角频率。因此,C=1 μF时,各扰动分量的误差频率函数为:

其中,m为超前矫正的超前程度。m过大则矫正过度,会给系统带来更差的补偿性能,m过小则达不到死区补偿效果。考虑滤波器的延时,本文采用滞后5拍延时。系统误差在死区频率处的响应为0,说明PI与重复控制相结合下,死区效应的稳态误差为0。一般情况下,为了系统的稳定性,C取小于1的常数,这时误差响应不为0,但很接近于0,开关死区带来的低频干扰在PI与重复控制相结合作用下几乎为0。
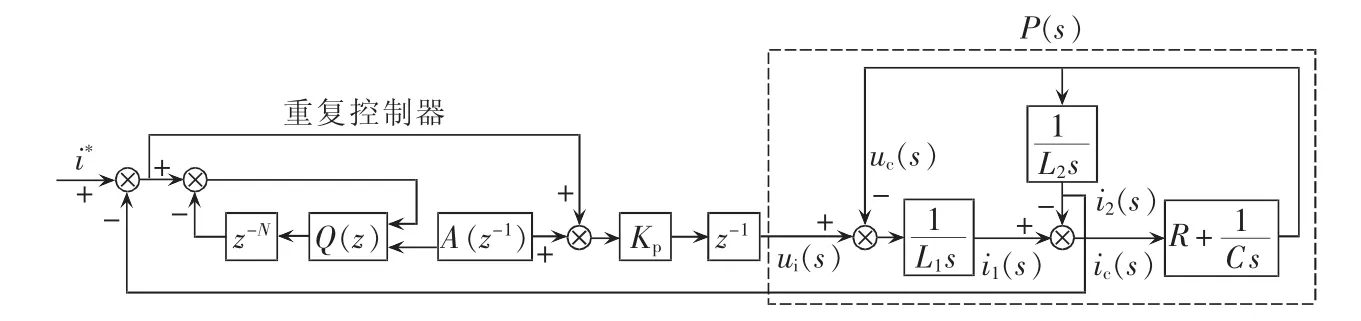
图4 重复控制电流环运算模型Fig.4 Operational model of current loop with repetitive control
2 仿真结果分析
本文基于MATLAB/Simulink平台进行仿真实验,具体参数取值如下:LCL滤波器中L1=1 mH,L2=0.2 mH,C=9.3 μF,阻尼电阻 R=0.8 Ω,开关频率 Fs=9 kHz,Kp=6。
图5由上至下依次给出了不加死区、加入死区及加入死区且补偿死区的指令电流i*与实际电流i波形图。通过对比图5所示的波形可以发现,加入死区后的电流波形比不加死区的跟踪误差大,实际电流不能按指令电流进行零误差跟踪;而用死区补偿后得到的波形不仅消除了死区效应带来跟踪误差较大的问题,而且能对指令电流突变处进行很好的控制,使得该处跟踪误差很小,避免了不加死区的波形中出现的指令电流突变处有较大的电流尖峰的问题。
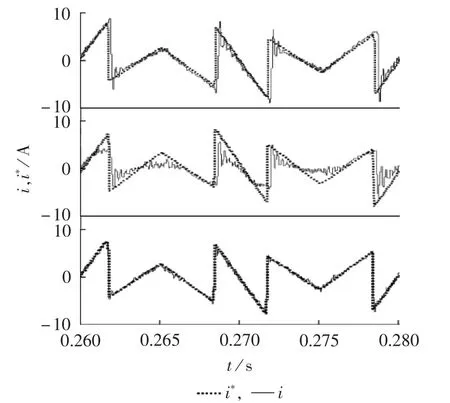
图5 Td=2.8 μs时电流波形Fig.5 Current waveform when Td=2.8 μs
图6给出了a相谐波源负载电流以及补偿死区前后网侧电流波形。图中,由上至下依次为谐波源负载电流iL、不考虑死区和加入死区且进行补偿的网侧电流ig仿真波形。对比可以发现,补偿死区后的波形比不考虑死区的波形拥有更高的正弦度,网侧电流在指令电流突变处尖峰值更小。
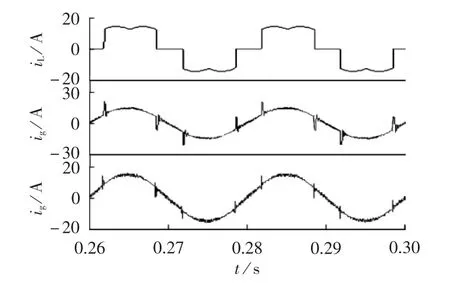
图6 网侧电流与负载电流波形Fig.6 Waveforms of grid-side current and load current
图7给出了无死区补偿的电流环波特图。从图中可以看出,系统在LCL谐振频率(3.11 kHz)处闭环增益为2.14 dB,增益较大,不能对谐振峰进行有效的衰减。图8给出了加入死区效应补偿后的电流环波特图。从图中可以看出,在谐振频率及以上频率处闭环增益均在0以下,说明系统可以对谐振峰及高频谐波进行有效的衰减,且保持原系统足够大的带宽,以保证系统响应的快速性。

图7 无死区补偿的电流环Bode图Fig.7 Bode diagram of current loop without dead-time compensation
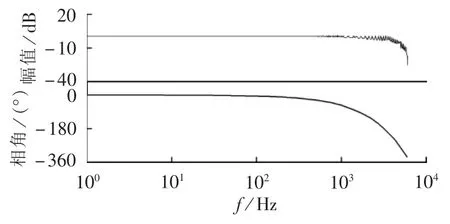
图8 带死区补偿的电流环Bode图Fig.8 Bode diagram of current loop with dead-time compensation
综上所述,通过对比仿真结果,可以得出结论:死区效应加大了跟踪误差,较未加死区系统,加大了网侧电流畸变率;本文采用的死区补偿控制消除了死区带来的影响,使得实际电流接近零误差跟踪指令电流;加入死区补偿控制后系统依然具有补偿前系统的响应带宽,保证了系统响应的快速性。
3 实验结果分析
为验证上述死区补偿控制在实际工程中的有效性,搭建10 kW二极管箝位型三电平并联型APF实验平台,控制芯片选用DSP TMS320F2812。采用LCL 滤波器,设置 L1=1 mH,L2=0.2 mH,C=20 μF,直流侧电压为730 V。电路主拓扑如图9所示。图10给出了死区补偿前后a相网侧电压ug、网侧电流ig的波形。
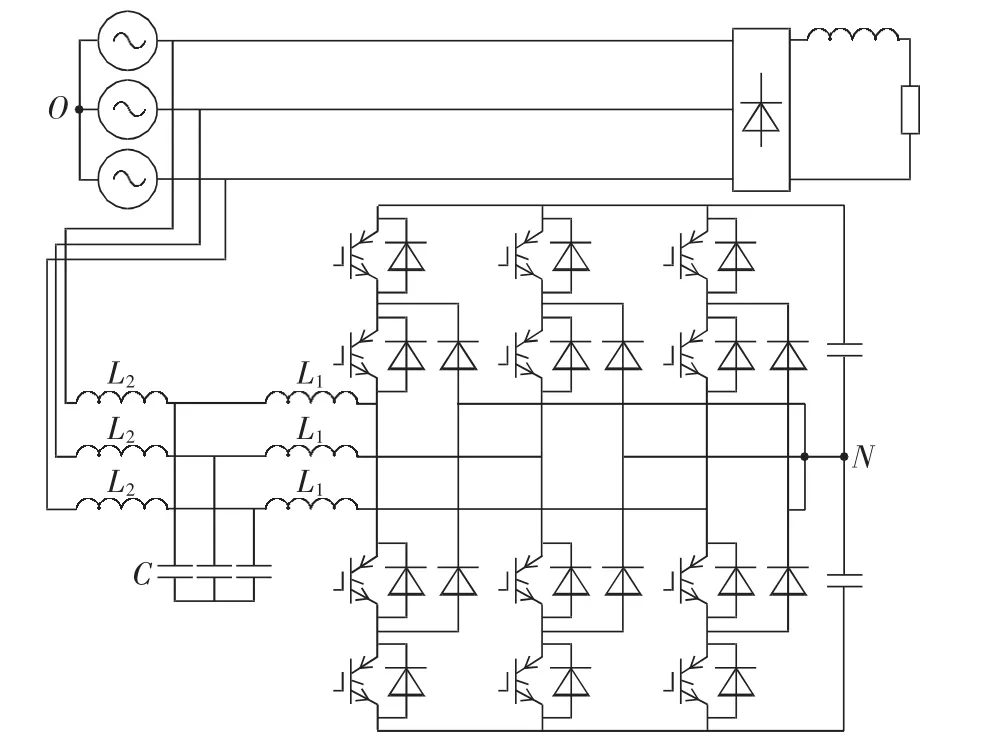
图9 LCL三电平并联型APF主电路拓扑Fig.9 Main circuitry topology of LCL three-level APF
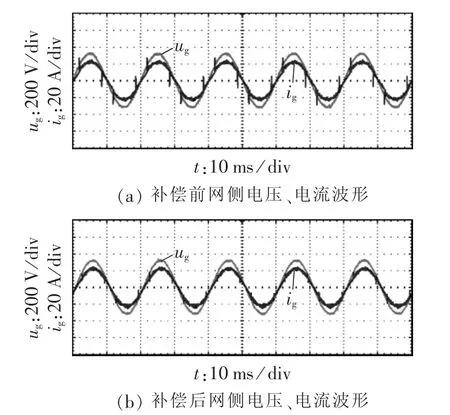
图10 死区补偿前后网侧电压、电流波形Fig.10 Waveform of grid side current and voltage with and without dead-time compensation
从图10可以看出,补偿后的波形具有很小的电流畸变率。在电流尖峰处,补偿前由于死区效应等因素导致输出波形在电平跳变处有很大的尖峰值,跟踪误差较大;而补偿后该现象得到极大的改善,尖峰值显著降低。
4 结论
根据APF的工作特性,本文详细讨论了死区效应生成原理,从三电平APF开关状态方程出发,推导出电流跟踪误差与死区时间之间的代数关系,阐释了死区时间对APF的补偿性能的影响。在此基础上提出了基于PI与重复控制相结合的补偿方式,给出了控制环节设计并分析了其作用。通过仿真对比,显示了具有死区补偿性能的系统兼备快速性与较好的稳态性。最后给出了补偿后的电流仿真波形与实验波形,结果显示所提方法能很好地抑制死区效应带来的不利影响。
参考文献:
[1]魏学良,戴珂,方昕,等.三相并联型有源电力滤波器补偿电流性能分析与改进[J]. 中国电机工程学报,2007,27(28):113-119.WEI Xueliang,DAI Ke,FANG Xin,et al.Analysis and improvement of current performance of three phase shunt active power filter[J].Proceedings of the CSEE,2007,27(28):113-119.
[2]陈国柱,吕征宇,钱照明.有源电力滤波器的一般原理及应用[J].中国电机工程学报,2000,20(9):17-21.CHEN Guozhu,LÜ Zhengyu,QIAN Zhaoming.The general principle of active filter and its application[J].Proceedings of the CSEE,2000,20(9):17-21.
[3]张东江,仇志凌,李玉玲.基于LCL滤波器的高稳态性能并联有源电力滤波器[J]. 电工技术学报,2011,26(6):137-143.ZHANG Dongjiang,CHOU Zhiling,LI Yuling.High performance parallel active power filter based on LCL filter[J].Transactions of China Electrotechnical Society,2011,26(6):137-143.
[4]王正仕,陈辉明.具有无功和谐波补偿功能的并网逆变器设计[J]. 电力系统自动化,2007,31(13):67-71.WANG Zhengshi,CHEN Huiming.Design of grid-tied inverters with the functions of reactive and harmonic compensation [J].Automation of Electric Power Systems,2007,31(13):67-71.
[5]MATTAVELLI P.A closed-loop selective harmonic compensation for active filters[J].IEEE Transactions on Industry Applications,2001,37(2):81-89.
[6]吴茂刚,赵荣祥,汤新舟.正弦和空间矢量PWM逆变器死区效应分析与补偿[J]. 中国电机工程学报,2006,26(12):101-105.WU Maogang,ZHAO Rongxiang,TANG Xinzhou.Dead-time effect analysis and compensation of SPWM and SVPWM inverter[J].Proceedings of the CSEE,2006,26(12):101-105.
[7]URASAKI N,SENJYU T,UEZATO K.Adaptive dead-time compensation strategy for permanent magnet synchronous motor drive[J].IEEE Transactions on Energy Conversion,2007,22(2):271-280.
[8]刘亮,邓明高,欧阳红林,等.基于预测电流控制的PWM逆变器死区补偿方法研究[J]. 电工技术学报,2005,20(8):78-83.LIU Liang,DENG Minggao,OUYANG Honglin,et al.A method to compensate the dead time of PWM inverter based on predictive current control[J].Transactions of China Electrotechnical Society,2005,20(8):78-83.
[9]张冲,王鹿军,金利祥,等.基于电流预测的三电平死区补偿方法[J]. 太阳能学报,2014,35(9):1581-1585.ZHANG Chong,WANG Lujun,JIN Lixiang,et al.A method to three-level dead-time compensation based on current prediction[J].Acta Energiae Solaris Sinica,2014,35(9):1581-1585.
[10]赵鲁,李耀华,葛琼璇,等.单相PWM整流器死区补偿方法[J].电机与控制学报,2015,19(6):6-14.ZHAO Lu,LI Yaohua,GE Qiongxuan,et al.Dead time compensation method of single-phase PWM rectifier[J].Electric Machines and Control,2015,19(6):6-14.
[11]周华伟,温旭辉,赵峰,等.一种新颖的电压源逆变器自适应死区补偿策略[J]. 中国电机工程学报,2011,31(24):26-32.ZHOU Huawei,WEN Xuhui,ZHAO Feng,et al.A novel adaptive dead-time compensation strategy for VSI[J].Proceedings of the CESS,2011,31(24):26-32.
[12]于晶荣,粟梅,孙尧.有源电力滤波器的改进重复控其优化设计[J]. 电工技术学报,2012,27(2):236-241.YU Jingrong,SU Mei,SUN Yao.Improved repetitivecontrol and its optimization for active power filter[J].Transactions of China Electrotechnical Society,2012,27(2):236-241.
[13]武健,何娜,徐殿国.重复控制在并联有源滤波器中的应用[J].中国电机工程学报,2008,28(18):66-71.WU Jian,HE Na,XU Dianguo.Application of repetitive control technique in shunt active power filter[J].Proceedings of the CSEE,2008,28(18):66-71.
[14]王成智,邹旭东,许赟,等.采用改进重复控制的大功率电力电子负载[J]. 中国电机工程学报,2009,29(12):1-9.WANG Chengzhi,ZOU Xudong,XU Yun,et al.Improved repetitive control scheme for power electronic load[J].Proceedings of the CSEE,2009,29(12):1-9.
[15]王果,周末,常文寰.适用于高速铁路的三相四开关型滤波器的电流重复控制设计[J]. 电力自动化设备,2016,36(2):71-77.WANG Guo,ZHOU Mo,CHANG Wenhuan.Repetitive current control of three-phase four-switch APF for high-speed railway[J].Electric Power Automation Equipment,2016,36(2):71-77.
[16]黄海宏,王钰,许若冰,等.双环重复控制三相四线制有源电力滤波器[J]. 电力自动化设备,2016,36(4):40-44.HUANG Haihong,WANG Yu,XU Ruobing,et al.Three-phase four-wire active power filter with dual-loop repetitive control[J].Electric Power Automation Equipment,2016,36(4):40-44.黄海宏(1973—),男,江西清江人,教授,博士,主要研究方向为电力电子技术(E-mail:hhh@ipp.ac.cn);

