不同工作模式下基于谐波电流有效值分级标准的CRT参数设计

郭毅娜 ， 田铭兴 ，原东昇

（1.兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070；2.兰州交通大学 甘肃省轨道交通电气自动化工程实验室，甘肃 兰州 730070；3.西安交通大学 电力设备电气绝缘国家重点实验室，陕西 西安 710049）

0 引言

变压器式可控电抗器CRT（Controllable Reactor of Transformer type）是一种新型的无功补偿设备，能有效解决长距离超高压输电线路的无功平衡和电压稳定问题［1-5］。CRT本质上相当于一种多绕组的变压器，以往文献多以谐波电流含有率作为绕组的分级原则，并通过增加控制绕组的级数来提高容量［6-9］。但是，对于大容量、高电压等级的CRT而言，控制绕组数过多会造成绕组耦合复杂、绕组容量利用率降低、磁集成设计困难［10-11］。

国标GB／T 14549—93《电能质量 公用电网谐波》对谐波电流允许的最大值是以有效值的形式给出的。据此可知，以k次谐波电流含有率作为CRT控制绕组分级标准时，会出现谐波含有率很高但实际注入电网谐波电流有效值（满足电网谐波电流要求）很小的情况［12-14］。故基于谐波电流含有率的绕组分级标准是不经济的，应该以谐波电流有效值作为绕组分级标准。同时，CRT各级控制绕组工作次序的不同衍生出多种工作模式，且工作模式与控制绕组级数、各级电流和谐波电流之间存在着一定的制约关系［15-16］。因此，仅基于一种工作模式对CRT进行参数设计是不完善的。

综上所述，为了在满足电网谐波电流要求的条件下尽可能地减少控制绕组的级数，以注入电网的谐波电流有效值作为谐波要求及控制绕组分级标准，并且在不同工作模式下对CRT控制绕组级数、各级电流分配及谐波电流等参数进行设计有着积极的意义。

1 谐波电流有效值分级标准

图1为CRT工作原理图。图中，W0为工作绕组，其直接并联在高压电网母线上；Wl为各级控制绕组（l=1，2，…，N；后同）；VThl为串联在控制绕组中的反并联晶闸管阀组；i0为工作绕组电流；il为各控制绕组电流；u为电网电压；ul为各控制绕组电压。通过合理控制控制绕组的工作次序，即可实现空载功率到额定功率的连续调节。

图1 CRT工作原理图Fig.1 Operation principle diagram of CRT

若忽略绕组电阻的影响，且不考虑控制绕组间的互漏抗、工作绕组的自漏抗以及铁芯的饱和特性，可得折算至工作绕组的CRT等效电路如图2所示，各支路依次对应各级控制绕组。图中，xl为各控制绕组的等效电抗。

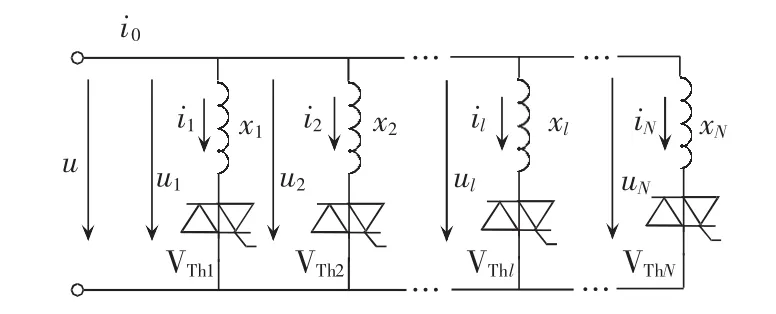
图2 折算至工作绕组的CRT等效电路Fig.2 Equivalent circuit converted to work winding of CRT

若选初始点为电源电压的正最大值时刻，则当晶闸管的导通角为 αl（0≤αl≤π／2）时，支路l中的电流为：

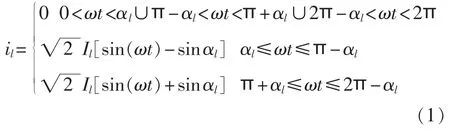
其中，Il=U／xl为支路l晶闸管触发角为0时电流有效值，即该支路额定电流。

对式（1）进行傅里叶分解，可得：

其中，Il1和Ilk分别为支路l的基波电流有效值及k（k=3，5，7，…）次谐波电流有效值。

原则上，CRT有多种工作模式，单支路工作模式指在任意时刻只有1条支路处于调节状态，其他支路处于全导通或截止的工作模式。与其他工作模式相比，单支路工作模式简单经济，因此本文的研究基于单支路工作模式，同时认为只有处于调节状态的支路中存在谐波。

由图2可知，在单支路工作模式下，CRT注入电网的谐波电流应等于处于调节状态的这条支路中的谐波电流。因此，要判断CRT注入电网的谐波电流是否满足要求，只需关注CRT处于调节状态的支路中的谐波电流大小。

对支路l而言，其处于调节状态时支路中的谐波电流为Ilfk（αl）。设电网要求CRT引入的最大k次谐波电流为Ikmax，若要满足谐波要求，则有：

式（3）即为基于谐波电流有效值的分级标准。由该式可知，只要CRT单支路工作模式下处于调节状态的支路注入电网的谐波电流有效值不大于给定值，就认为它是满足谐波要求的。

2 工作模式分析

CRT的工作模式是指各级控制绕组中反并联晶闸管的工作形式和次序。本文就CRT的3种经典单支路工作模式进行分析和参数设计。

2.1 顺次单支路工作模式

从零功率到额定功率调节过程中，图2中支路1中的VTh1最先开始调节并达到全导通，而其余支路为全截止；接着VTh2开始调节并达到全导通，除支路1、2外的支路全截止；依次顺序，直到VThl处于调节状态时，支路 1、2、…、l-1 全导通，支路 l+1、l+2、…、N全截止。负载减小时按上述过程的逆过程工作。这即是顺次单支路工作模式。

在该模式下，处于调节状态的支路l的k次谐波电流有效值满足如下关系：

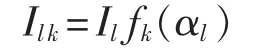
考虑到谐波电流需满足设计要求，则有：

在忽略绕组电阻和磁饱和的影响条件下，各支路额定电流瞬时值同相位，因此，CRT的额定电流有效值等于各支路额定电流之和，即：

对式（4）不等式两边同除以后可得：

同时，令容量递增系数为：

其中，m=1，2，…，N 且 m≤l。

对式（6）不等式两侧分子分母同除以再将式（7）代入可以得出：

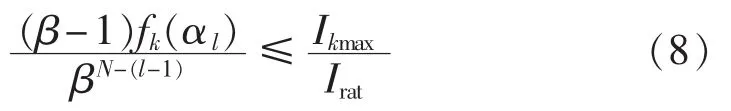
从式（8）可以看出，只要当l=N（即支路N处于调节状态）时的谐波满足要求，则其余情况下的谐波均满足要求。即有：

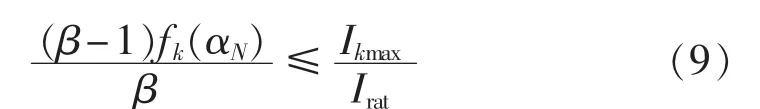
当CRT的额定电流确定后，根据式（9）求得满足最大谐波电流时的容量递增系数β为：

进而求得支路数N以及任意支路l的电流为：

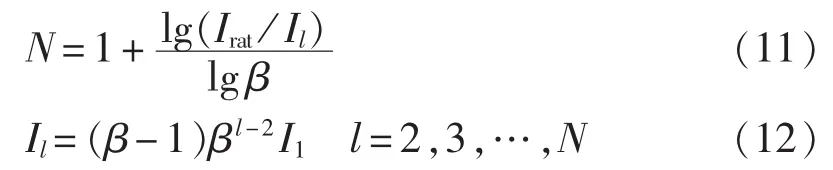
2.2 固定单支路工作模式

在CRT的整个调节范围内，始终都让容量最小的支路处于调节状态，而其余支路要么全导通，要么全截止，称这种工作模式为固定单支路工作模式。

该模式下，为实现功率的平滑调节，支路额定电流必须按照特定规律进行设计，即：

其中，N＞1。

按此规律，支路1的晶闸管全导通后其额定电流瞬时转移到支路2，支路2承担了支路1的全部电流，支路1的电流回归为0后继续开始调节。其余工作状态均与此类似。

该模式下，仅有容量最小的支路处于调节状态（设定支路1为调节支路），在谐波电流分析时只需关注这一支路，此时注入电网的谐波为 I1fk（α1），当I1fk（α1）≤Ikmax时，满足谐波要求。

由并联分流原理和固定单支路工作模式下的支路电流分配原则可知，总并联支路数N以及任意支路l的电流为：

2.3 转移单支路工作模式

转移单支路工作模式的工作原理是：随着负载从0开始增大，支路1中的晶闸管开始调节至全导通后，支路1中的电流I1转移到支路2，支路2承担支路1的电流并从I1的基础上开始调节至全导通，而支路1的电流回归为0，如此直到支路N全导通后，再从头开始调节支路1。负载减小时按上述过程的逆过程工作。

该模式下，为满足容量的平滑调节，转移过程需满足如下条件［16］：

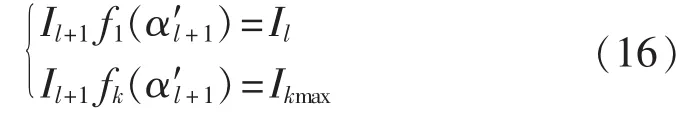
式（16）表明，当支路l的电流转移到支路l+1时，要控制支路l+1的导通角αl+1，使得在转移瞬间满足如下条件：支路l+1的基波电流和k次谐波电流分别等于支路l的额定电流Il和给定最大k次谐波电流 Ikmax，转移瞬间导通角为α′l+1。该工作模式下，在已知支路1电流的前提下，其他支路电流可通过递推算法依次求得，因此支路1电流是计算其他支路电流的基础。

由以上分析可知：不同的工作模式下，支路1电流I1是计算CRT支路数N和支路电流的基础；而支路1的电流I1大小受到谐波电流的制约。

3 参数设计

CRT进行参数设计的目的之一是在满足谐波电流要求的前提下尽可能地减小支路数，并求得对应各支路的电流分配。因此，确定符合条件的支路1的电流I1是设计计算CRT支路数N和支路电流等参数的基础。

3.1 支路1电流的确定

给定k次谐波电流最大值Ikmax，CRT工作在单支路工作模式下时，其注入电网的谐波电流满足式（4）要求。

为使支路l在调节过程的任意角度下都能满足谐波要求，则其电流有效值取值范围满足：

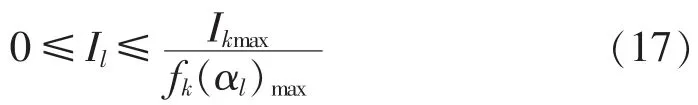
其中，fk（αl）max为支路 l在调节的过程中 fk（αl）的最大值。

当l=1时，可得支路1的取值范围，即：

同时，将支路1的电流I1最大值作为计算支路数N等参数的初值，即：

3.2 不同工作模式参数设计

确定支路1的电流I1初值后，结合不同工作模式的特点，可求得对应支路数N和支路电流。但是无论哪种工作模式下，参数的计算结果均应满足以下条件：CRT支路数N为整数，若N的计算结果为小数，需要对N向上取整；各个处于调节状态的支路注入电网的谐波电流都应满足式（17）的谐波要求；各支路电流之和应满足式（5）要求，即各支路额定电流之和等于CRT额定电流。若不满足以上任一条件，说明所确定的支路1电流初值取值不合理，对支路1电流初值进行调整，并重新计算各参数。

3.2.1 顺次单支路工作模式参数设计

首先根据式（10）求得满足最大谐波电流时的容量递增系数β后，将该值与根据式（18）确定的支路1电流I1初值代入式（11）求得支路数N。若支路数N计算结果为小数，说明支路1电流初值取值不合理，对计算结果进行取整，将取整后的支路数N代入式（11）中重新计算支路1电流I1，该值为修正后的支路1电流值。将取整后的支路数N与修正后的支路1电流代入式（12）中，求得其余支路电流，并验证支路电流计算结果是否满足式（17）和式（5）。

3.2.2 固定单支路工作模式参数设计

与顺次单支路工作模式的设计方法类似，首先根据式（18）确定的支路1电流I1初值，将其代入式（14）求得支路数N，若支路数N计算结果为小数，对计算结果进行取整，将取整后的支路数N代入式（14）中重新计算支路1电流I1，该值为修正后的支路1电流值。将取整后的支路数N与修正后的支路1电流代入式（15）中，求得其余支路电流，并验证支路电流计算结果是否满足式（17）和式（5）。

3.2.3 转移单支路工作模式参数设计

转移单支路工作模式下，支路数N没有确定的表达式，需根据CRT额定电流结合谐波电流进行分析确定。

令：

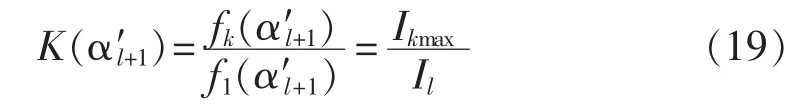
首先根据式（18）计算支路1电流I1初值，在已知最大k次谐波电流Ikmax前提下，根据式（19）先求得支路1电流转移至支路2瞬间的晶闸管导通角α′2，代入式（16）得到支路2电流。同理，根据支路l电流Il及最大 k 次谐波电流 Ikmax，结合式（19）和式（16）可计算求得支路l电流转移至支路l+1瞬间晶闸管导通角α′l+1以及对应的支路电流Il+1。

判断所确定的晶闸管调节范围与支路电流是否合理的依据是：晶闸管导通角αl+1在从α′l+1至0°调节过程中，支路l+1出现的谐波电流不能超过最大k次谐波电流 Ikmax，即保证 Il+1fk（αl+1）≤Ikmax。

当谐波电流满足条件时，应判断所确定的支路电流之和是否满足式（5）要求，即若所确定的支路电流之和超过CRT额定电流，即需要对支路1电流I1进行调整，并按照上述过程重新计算各支路电流至满足式（17）和式（5）要求，并得到满足谐波电流要求的支路数N=l+1。

若所确定的支路电流之和小于CRT额定电流，即，将该晶闸管范围对应支路电流作为初值计算下一条支路电流，并按上述过程再次判断各支路电流是否满足式（17）和式（5）。

3.3 不同工作模式支路数大小比较

为了叙述方便，把顺次单支路、固定单支路数和转移单支路工作模式的支路数分别记为Nsh、Ngu和Nzh。

当k=5时，对式（2）的第2个式子求极值可得f5（αl）在 0≤αl≤π／2 范围内的极值点为：

通过分析计算可知：与是 f5（αl）在 0≤αl≤π／2 范围内的 2 个极大值点。

由式（10）和式（11）可以知道，顺次单支路工作模式下，支路数的大小与最大k次谐波电流Ikmax有关。

比较式（11）和式（14）可以知道：当时，Nsh≤Ngu；当 β＜2（I5max＜0.025Irat）时，Nsh＞Ngu。

对式（2）的第1个等式进行求导分析可知f1（αl）在0≤αl≤π／2范围内单调递减且满足：

由式（20）、式（16）可得：

从而得：

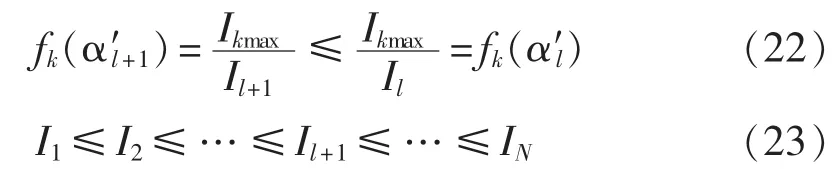
由式（22）、式（23）可得各支路电流5次谐波系数满足：

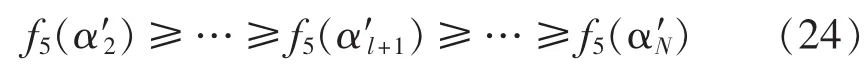
转移单支路工作模式下支路l向支路l+1转移瞬间谐波电流等于Ikmax，且从α′l+1调节至完全导通的整个过程中谐波电流始终不能超过Ikmax。

当时，支路 l+1 在调节至导通过程中实际注入电网的谐波电流超过Ikmax，因此，转移瞬间晶闸管导通角范围为时，CRT实际注入电网谐波电流可满足要求。

在范围内，f5（αl）单调递增，因此，由式（24）可知：α′2≥ … ≥ α′l+1≥ … ≥α′N。

而由前文分析可知，f1（αl）在 0≤αl≤π／2 范围内单调递减，因此得：

将式（16）的第1个式子进行化简得：

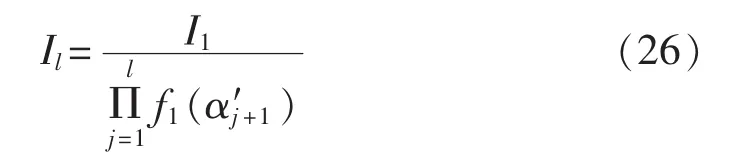
由式（25）、式（26）可得：

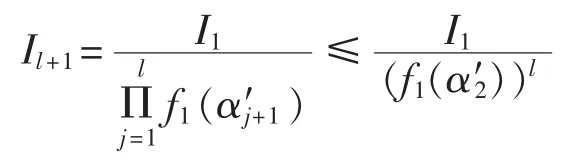
因此得：

其中，

将式（27）进行化简可得，将该不等式两边取对数后得：

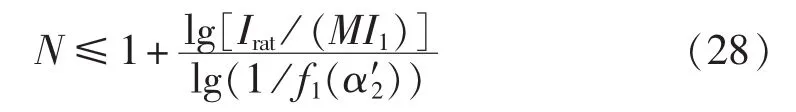
式（28）为转移单支路工作模式下支路数Nzh的范围。

当 k=5 时，的取值范围为：

即 1.67≤1 ／f1（α′2）≤3.33。

由式（28）、式（29）可知，转移单支路工作模式下支路数与转移瞬间的晶闸管导通角有关。

比较式（14）与式（28）可知：当 1 ／f1（α′2） ≥ 2时，由于 M≥1，则 Nzh≤Ngu；当 1 ／f1（α′2）＜2 时，Nzh＞Ngu。

需要说明的是，以上分析只是对于3种工作模式下支路数数值大小的比较，但由于支路数只能是整数，需将计算出的结果向上取整，因此，可能存在不同工作模式下支路数数值大小不同而实际中支路数相同的情况。同时，根据取整后的支路数重新计算的支路1电流小于或等于其初值，由式（3）可判断不同工作模式下各支路实际注入电网的谐波电流不会超过给定最大k次谐波电流值，因此谐波总是满足要求。

此外，固定单支路工作模式因为只有固定的1条支路需要调节，所以其控制较其他2种工作模式最简单。

4 算例

设一CRT工作于工频状态，额定电流Irat=208A，同时电网规定其引入的最大5次谐波电流I5max=3.8 A。

4.1 顺次单支路工作模式参数设计

顺次单支路工作模式下各支路是顺序导通的，由式（17）可得任意支路l电流有效值取值范围为0≤Il≤76.00 A。由式（18）可知支路1电流初值为I1＝76.00A。 由式（10）可知级间容量递增系数 β=1.57。将I1、β的值代入式（11）可得满足最大谐波的最小支路数为：

由于N的计算结果为小数，需对N向上取整，则N=4。将取整后的支路数代入式（11）重新计算I1，可得修正后的I1=53.74 A。

根据式（12）可得其余支路的电流有效值为：I2=30.64 A，I3=48.09 A，I4=75.53 A。

4.2 固定单支路工作模式下参数设计

固定单支路工作模式下只有支路1处于调节状态。由式（18）可得支路1电流有效值的取值范围为0≤I1≤76.00 A。由式（18）可得支路1电流初值为I1=76.00 A。将I1值代入式（14）可得满足最大谐波的最小支路数为：

由于N的计算结果为小数，需对N向上取整，则N=3。将N代入式（14）重新计算I1，可得修正后的I1=52.00 A。

根据式（15）可得其余支路的电流有效值为：I2=52.00 A，I3=104.00 A。

4.3 转移单支路工作模式下参数设计

由式（17）可得任意支路l的电流有效值取值范围为0≤Il≤76.00 A。由式（18）可得支路1电流初值I1=76.00 A。

转移单支路工作模式下，容量最小的支路1最先开始处于调节状态，支路1在调节过程中可能出现的5次谐波电流最大值I5max=3.80 A。

根据式（19）可得：

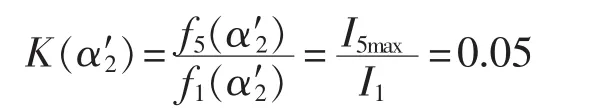
通过计算可知支路1中电流向支路2转移时符合条件的晶闸管触发角为α′2=0.46 rad。根据式（16）可得α′2对应的支路2的电流值为：

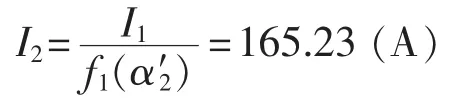
在晶闸管导通角从0.46 rad至0的调节过程中，支路2出现的最大谐波电流为3.80 A，谐波电流满足要求。

对I2而言，由于I1+I2＞Irat=208.00 A，此时需对支路1的电流值进行微调，并按上述过程重新计算直至满足式（5）要求。 经计算，当I1=65.53 A、I2=142.47A时满足式（17）和式（5）要求，此时，1 ／f1（α′2）=2.17，支路数N=2。

4.4 比较分析

基于谐波电流有效值分级标准对CRT在3种单支路工作模式下的参数设计取值结果进行对比，如表1所示。

由表1可知，3种工作模式下，各支路在调节过程中实际注入电网的谐波电流均满足式（17）要求，即谐波电流不超过给定最大值，各支路电流之和满足式（5）要求。

支路1的电流分配相差不大时，固定单支路工作模式的谐波电流最小。同时，在注入电网谐波电流均满足要求的情况下，顺次单支路工作模式β=1.57＜2，支路数最多。 转移单支路工作模式下 1 ／f1（α′2）=2.17＞2，支路数最少，算例结果符合理论分析结论。

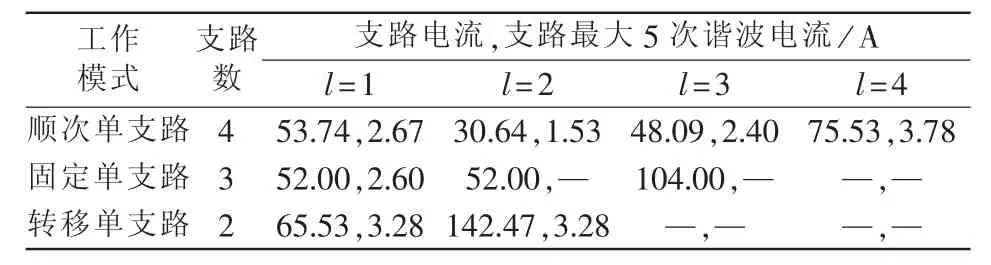
表1 不同工作模式下CRT参数取值结果对比Table 1 Comparison of parameters in different operation modes

5 结论

a.CRT支路数与支路1电流、最大k次谐波电流和工作模式紧密相关。

b.基于谐波电流有效值的分级标准进行参数设计时，不同工作模式下的CRT支路数不同。

c.在CRT额定容量、支路1电流确定的前提下，固定单支路工作模式下支路数确定，顺次单支路工作模式下支路数与最大k次谐波电流有关，转移单支路工作模式下支路数与转移瞬间的晶闸管导通角有关。

d.不同工作模式下CRT实际注入电网的k次谐波电流均不超过电网给定的最大值，谐波电流满足要求。支路1电流分配相差不大的情况下，固定单支路工作模式下的谐波电流最小。

e.就本文算例而言，转移单支路工作模式的控制支路数最少，而固定单支路工作模式谐波电流最小。考虑到固定单支路工作模式控制最简单，所以，综合而言，固定单支路工作模式最优。

参考文献：

［1］张丽，徐玉琴.并联电抗器在超（特）高压电网中应用及发展［J］.电力自动化设备，2007，27（4）：75-78.ZHANG Li，XU Yuqin.Application and development of shunt reactors in EHV&UHV transmission lines［J］.Electric Power Automation Equipment，2007，27（4）：75-78.

［2］周勤勇，郭强，卜广全，等.可控电抗器在我国超／高压电网中的应用［J］. 中国电机工程学报，2007，27（7）：1-6.ZHOU Qinyong，GUO Qiang，BU Guangquan，et al.Application of controllable reactors in China’s power grid and extra and ultra and voltage level［J］.Proceedings of the CSEE，2007，27（7）：1-6.

［3］田铭兴，石鹏太，马亚珍.n级饱和磁阀式可控电抗器结构特性和仿真方法［J］. 电力自动化设备，2016，36（2）：95-101.TIAN Mingxing，SHIPengtai，MA Yazhen.Structuralproperty and simulation method of n-stage saturable magnetic-valve controllable reactor［J］.Electric Power Automation Equipment，2016，36（2）：95-101.

［4］周腊吾，徐勇，朱青，等.新型可控电抗器的工作原理与选型分析［J］. 变压器，2003，40（8）：1-5.ZHOU Lawu，XU Yong，ZHU Qing，et al.Type selection analysis and principle of new controlable reator［J］.Transformer，2003，40（8）：1-5.

［5］SMIRNOV A A，SMOLOVIK S V.An improvement of Russian long-length AC electrical energy transmission systems by implementation of controllable shunt reactors［C］∥2005 IEEE Russia Power Tech.St.Petersburg，Russia：IEEE，2005：1-5.

［6］田军，陈乔夫，张宇.多绕组变压器负载可控型可调电抗［J］.电力自动化设备，2010，30（1）：32-35.TIAN Jun，CHEN Qiaofu，ZHANG Yu.Adjustable reactor with controllable load of multi-winding transformer［J］.Electric Power Automation Equipment，2010，30（1）：32-35.

［7］张宇，陈乔夫，田军，等.基于变压器端口调节的可控电抗器［J］.中国电机工程学报，2009，29（18）：113-118.ZHANG Yu，CHEN Qiaofu，TIAN Jun，et al.Controllable reactor based on transformer winding current regulating［J］.Proceedings of the CSEE，2009，29（18）：113-118.

［8］TIAN Mingxing，LI Qingfu，LI Qunfeng.A controllable reactor of transformertype［J］.IEEE Transactions on PowerDelivery，2004，19（4）：1718-1726.

［9］田铭兴.变压器式可控电抗器的基本理论研究［D］.西安：西安交通大学，2005.TIAN Mingxing.Basic theoretical research on controllable reactors of transformer type［D］.Xi’an：Xi’an Jiaotong University，2005.

［10］田铭兴，原东昇，安潇，等.变压器式可控电抗器绕组电流分析［J］. 高电压技术，2014，40（1）：22040-22045.TIAN Mingxing，YUAN Dongsheng，AN Xiao，et al.Analysis on winding current of controllable reactor of transformer type［J］.High Voltage Engineering，2014，40（1）：22040-22045.

［11］田铭兴，尹健宁，柳轶彬，等.基于磁集成技术的变压器式可控电抗器的结构设计与分析［J］. 高电压技术，2014，40（5）：30620-30628.TIAN Mingxing，YIN Jianning，LIU Yibin，et al. Structure design and analysis of controllable reactor of transformer type based on magnetic integration technology［J］.High Voltage Engineering，2014，40（5）：30620-30628.

［12］国家技术监督局.电能质量 公用电网谐波：GB／T 14549—93［S］. 北京：中国标准出版社，1993.

［13］田铭兴，安潇，原东昇，等.变压器式可控电抗器谐波系数定义与其控制级数的关系［J］. 电网技术，2014，38（1）：217-221.TIAN Mingxing，AN Xiao，YUAN Dongsheng，et al.Relationship between harmonic coefficients definition and power-step number of controllable reactor of transformer type［J］.Power System Technology，2014，38（1）：217-221.

［14］田铭兴，励庆孚.变压器式可控电抗器的谐波分析和功率级数计算［J］. 中国电机工程学报，2003，23（8）：168-171.TIAN Mingxing，LI Qingfu.Harmonic current and power-step number of controllable shunting reactor of transformation type［J］.Proceedings of the CSEE，2003，23（8）：168-171.

［15］田铭兴.多并联支路型可控电抗器工作模式［J］.电工技术学报，2006，21（12）：21-25.TIAN Mingxing.Operation mode of controllable reactor with multiple parallel branches［J］.Transactions of China Electrote-chnical Society，2006，21（12）：21-25.

［16］柳轶彬，田铭兴，尹健宁.变压器式可控电抗器单绕组调节模式及谐波电流优化［J］. 电力自动化设备，2015，35（7）：74-88.LIU Yibin，TIAN Mingxing，YIN Jianning. Single-winding regulating mode and harmonic current optimization of controllable reactor of transformer type［J］.Electric Power Automation Equipment，2015，35（7）：74-88.