基于变结构控制理论的高压直流附加频率控制器设计

赵 磊，刘天琪，李兴源

（四川大学 电气信息学院，四川 成都 610065）

0 引言

随着我国交直流互联电网的大力发展，带来巨大社会及经济效益的同时，其复杂的结构和运行方式也给电力系统的安全稳定提出了新的挑战，其中系统频率振荡是具有代表性的问题之一［1-2］。特别是系统处于基本只由若干个大型电厂与送端换流站群联接构成的孤岛运行时，系统由于阻尼不足，易受扰动影响出现频率偏移，甚至出现频率振荡超出稳定阈值的情况，导致系统失稳［3-5］。在抑制系统频率振荡的措施中，高压电流输电（HVDC）附加控制因其对直流输送功率的快速调节能力得到越来越广泛的应用。但在对控制器参数整定中，大多以试凑法或根据经验整定［6-9］，具有一定的盲目性，易出现整定不准确、控制效果不理想等问题；且文献［6-7］中控制器环节由多个模块组成，各模块之间相互影响，存在控制误差增大的问题，不利于实际工程应用。相比于鲁棒控制和传统比例-积分-微分（PID）控制，变结构控制具有对干扰和摄动的不变性、在滑动模态上的自适应性等特点，在控制器设计上更具优势。另一方面，为使控制效果更好，应对控制器参数进行优化，如文献［10］采用了遗传算法，但其优胜劣汰法则使下一代选择上只保留了最优解，次优解被舍弃，从而容易陷入局部最优，而且需要设置的参数较多，不便于实际工程应用。

基本粒子群优化（PSO）算法［11］需要设置的参数较少，便于实际工程应用；通过搜寻粒子个体最优及自身附近粒子的最优值来修正自身的方向和速度，获取更有效的记忆能力；并且在相互学习能力、处理多维多目标问题方面拥有一定优势，且可保持群体的多样性，用于非线性系统时具有较好的鲁棒性。但是，基本PSO算法在粒子更新中只考虑最佳位置，容易导致搜寻方向单一化；且在惯性权重取值上，不易有效维护全局和局部寻优的平衡。鉴于此，本文提出一种改进PSO算法用于控制器参数的优化。

本文首先采用最小二乘-旋转不变（TLSESPRIT）算法辨识出系统低阶模型，再基于二次最优型变结构控制理论设计HVDC附加频率控制器，最后利用极大极小值原理和改进PSO算法对控制参数进行优化。设计中选取线性切换函数和指数趋近律减小变结构控制的抖振及到达滑模面的时间，通过参数优化使特征值尽可能位于远离虚轴的左半平面。利用PSCAD／EMTDC对某实际系统模型进行仿真验证，结果表明该控制器对系统频率振荡具有较好的控制效果和较强的鲁棒性。

1 变结构控制理论

1.1 变结构控制基本原理

变结构控制由两部分组成：趋近运动和滑动模态。趋近运动是通过开关控制迫使系统由初始状态快速到达设定的切换面；滑动模态是使系统沿着切换面收敛于状态稳定点［12］。

变结构控制函数形式为：

其中，s（x）为切换函数。为了使系统的状态变量在有限时间内到达切换面，控制律应该满足如下到达条件：为使系统在滑动模态阶段，在切换面上逐渐稳定且具有良好的品质，应满足：s（x）=0。 函数 s（x）一般选取为线性函数，其表达式一般可简化为s（x）=Cx，其中矩阵C的求取是设计变结构控制器的重要环节，本文采取二次型性能指标的最优控制法来确定。为了加速趋近过程且削弱抖振，采取指数趋近率：=-ks。 k为正数，适当增大k可以加速趋近过程和提高控制效果［13］。

1.2 带观测器的变结构控制规律推导

对于一般线性系统而言，其状态方程为：

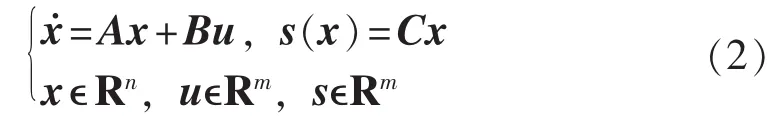
其中，x、u分别为系统状态向量、控制向量；n≥m≥1；A、B分别为系统状态矩阵、输入矩阵。首先将控制系统方程变换成可控标准型，在变换过程中考虑系统的开环传递函数并不发生变化。变换后系统的状态方程可以表示为：

由线性系统原理可知，原系统（A，B）可控，则（A11，A12）也可控，从而也可控。 通过对原系统和优化积分指标中的矩阵x和Q进行变换，转化为一个等价系统及最优指标如下：

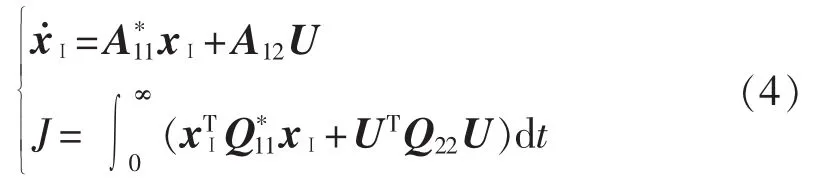
其中，定义由于矩阵Q半正定，则矩阵也都半正定，从而构成典型的以xⅠ为状态变量的二次型最优控制函数，对xⅠ进行优化控制。解式（4）可得xⅠ的最优解为：

其中，P为正定矩阵，它是里卡蒂方程的解［14］。 整理后得：

即切换面［C1C2］x=0，所以由（x）=C、=-ks、式（2）得Q22u=-ks，所以可得：

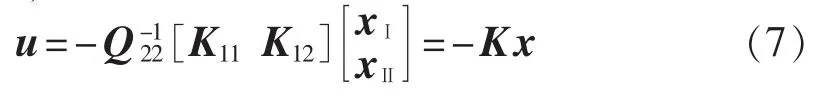
即

引入观测器增益矩阵［15］，对状态观测器中的状态方程式进行拉普拉斯变换可得：

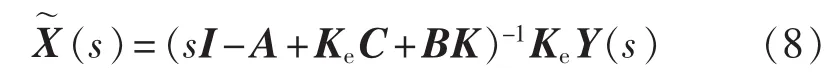
由于实际系统中某些状态变量无法通过物理方法测量，为此通过状态观测器，将观测状态用于反馈，同时省略原系统中不关心的信息，从而在保证控制的有效性的同时，降低控制器的复杂性［16］。变结构控制的状态观测反馈系统如图1所示，通过观测器中的增益矩阵Ke对系统中的估计误差不断进行修正，同时减小抖振。

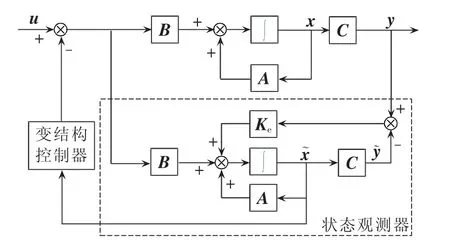
图1 变结构控制的状态观测反馈系统Fig.1 Observe-state feedback system with variable structure control

将式（8）代入式（7）中可得引入观测器后的控制律为：

2 控制器参数优化的改进PSO算法

由上述推导可知控制器性能及K的值取决于矩阵Q和指数趋近率参数k的取值。为寻求最优控制器参数Q和k来确保控制器在系统可能运行条件下获得较好的控制效果，可转化为求解式（10）所列的极大极小值优化问题。优化控制器参数来使式（2）闭环系统在可能运行状态下，特征值都最大限度地处于远离虚轴的左半平面。如果J＜0，则优化后的参数R1在运行条件R2下系统处于稳定，且J值越小系统越稳定。

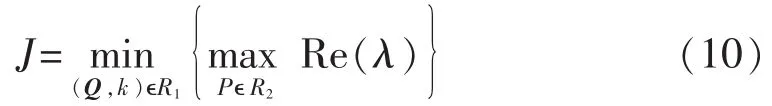
其中，R1为控制器参数的集合，即矩阵Q和k；R2为系统可能运行条件的集合，即直流线路的传输功率P；λ为系统特征值。考虑到目标函数的复杂性，其极值不易求解，本文采用一种改进PSO算法对其进行求解。

在N维空间中存在m个粒子［17］，其中第i个粒子在空间的位置为 Xi=（xi1，xi2，…，xiN），飞行速度为Vi=（vi1，vi2，…，viN），其中 i=1，2，…，m。 设定目标函数并将Xi代入来求取第i个粒子的适应值，对于粒子个体经历过的最佳位置（即具有最好适应值的位置）为 Pi=（pi1，pi2，…，piN），而全体粒子经历过的全局最佳位置 Pg=（pg1，pg2，…，pgN）。

从t代进化到t+1代后，粒子的更新速度和位置为：

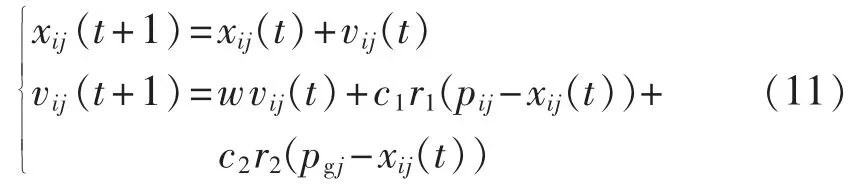
其中，w 为惯性权重，wϵ（0.4，1.2）；c1、c2为加速常数，c1，c2ϵ（0，2）；r1、r2为随机数，r1，r2ϵ（0，1）。

为了避免基本PSO算法中只考虑个体和全体粒子的最好适应值，而导致搜索方向单一化，甚至陷入局部最优，首先对每个粒子个体的适应值进行大小排序，然后通过对每个粒子的个体最佳位置分别乘以各自相应的权重系数，以其乘积的和来修正Pg。如果粒子的适应值越大，则其相应的权重系数越大，对粒子群的全局最佳位置影响也就越大，需同时兼顾每一个粒子的影响。设各粒子的位置权重系数为βij，则有：

其中，i=1，2，…，m；j=1，2，…，N。

同时，考虑PSO算法的性质以及惯性权重的特点，当w取值较大时，虽加强了全局搜索的能力，但大幅增加了运算量，降低了收敛速度；当w取值较小时，收敛速度加快，但易陷入局部最优。所以综合两方面，首先进行全局搜索，对w赋予较大的起始值，伴随搜索的进行逐步减小w值来提升寻优速率，从而确保算法在最佳位置附近进行精确搜索，兼顾算法的效率与精度。 本文选用正切函数 y=tanx（xϵ［0，π／4］）来模拟w的变化趋势，定义惯性权重w为：

其中，wmax、wmin分别为最大、最小惯性权重；K、Kmax分别为当前和最大迭代次数。

3 HVDC附加频率控制器设计

根据某实际电网在PSCAD／EMTDC中搭建仿真系统，所搭建的系统主要考虑500 kV线路以及该地区的大型电厂，对于220 kV线路和负荷进行适当的等值处理，最终的系统拓扑结构如图2所示。系统中电厂1、电厂2以及电厂5均含有2台汽轮发电机；电厂3与电厂4均由4台水轮发电机构成。其中，系统中发电机模型均包括励磁及调速系统，所有等值机均根据潮流网络动态等值方法进行相应等值；直流系统以25%功率（1 600 MW）单极运行，控制方式为整流侧定电流、逆变侧定关断角控制。

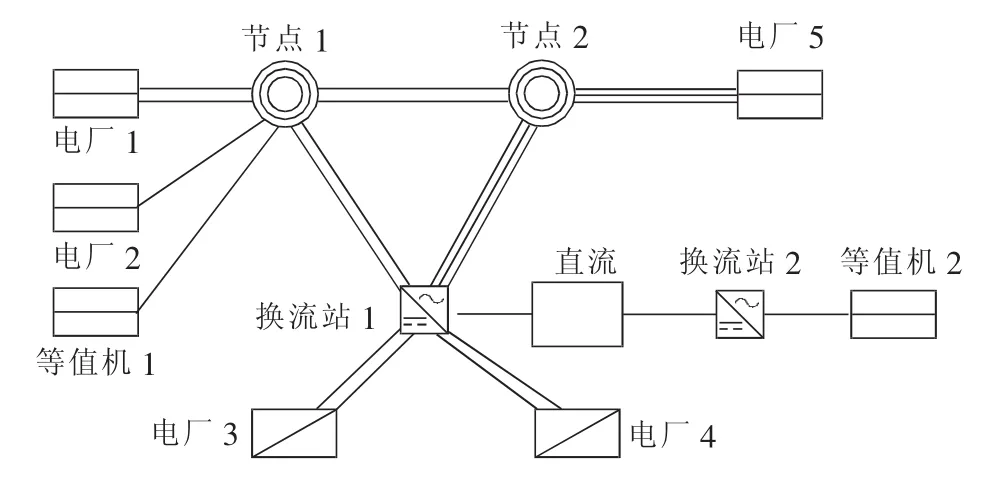
图2 某实际电网仿真系统网络结构Fig.2 Simulation system structure of a real power system

首先利用TLS-ESPRIT算法对系统进行辨识［18-20］，在直流系统整流侧定电流控制信号处施加不破坏系统可线性化条件的小扰动激励，并以送端交流系统频率偏差为输出，辨识得到系统几个主要振荡模态的低阶模型 G（s）为：

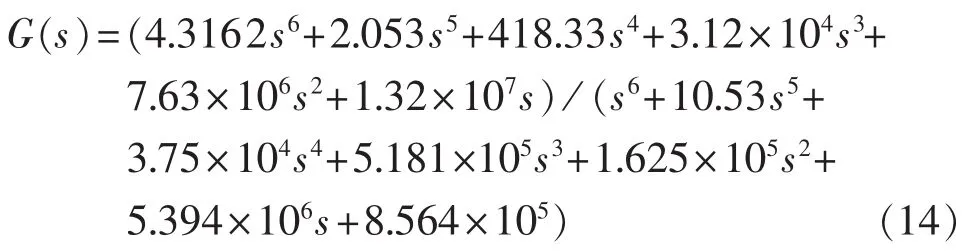
3.1 控制器结构

变结构附加频率控制器结构如图3所示，控制器中以系统频率偏差作为控制输入信号，作用于直流整流侧电流控制处，以附加电流控制信号为输出，用来调控直流线路的有功功率输送，从而抑制因扰动故障引起的发电机输出功率与直流输出功率不平衡引发的系统频率振荡。其中滤波环节采用Butterworth滤波器。由于通过直流附加进行控制，需要考虑通信时滞，通过Pade近似代替系统的时滞。图3中，Kp、Ti为系统PI控制环节的参数；G、T为系统积分控制环节的参数；Omax、Omin分别为限幅环节的上限值、下限值；I、Iord、α、Δf均为直流整流侧定电流控制的相关参数。

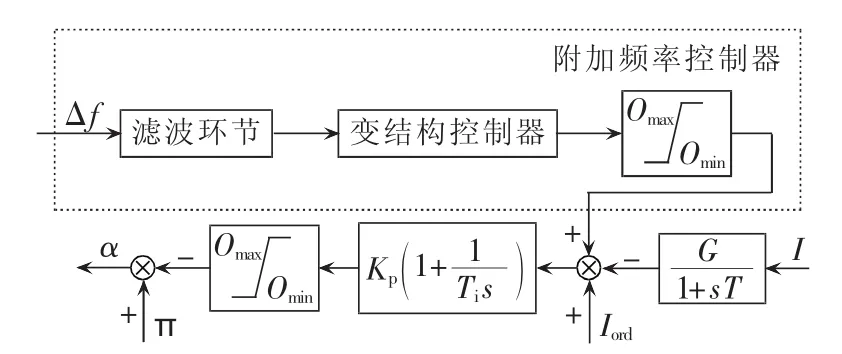
图3 直流系统附加频率控制器结构Fig.3 Diagram of HVDC additional frequency controller

3.2 控制器参数整定

已知矩阵Q为对角阵，其对角元素为qii（i=1，2，…，n），为确定控制器参数，现对矩阵Q的变量和变结构指数趋近率参数k进行优化，结合极大极小值原理，取式（10）所示的目标函数，定义为：

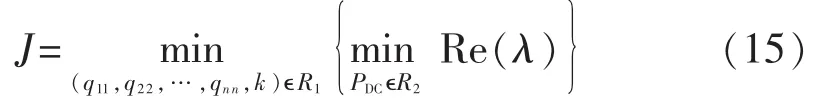
首先凭借经验得R1中矩阵Q的变量取值范围为 qiiϵ［0，100］，kϵ［1，100］；由直流系统的运行条件可知R2中的PDC=0.25。

使用改进PSO算法优化后，得出矩阵Q的各变量为 q11=95.946、q22=1.341、q33=1.117、q44=1.019、q55=1.081、q66=1.037 及参数 k=46.36，此时 J=-0.287。

最后通过变结构控制规律设计变结构附加频率控制器，同时考虑采用信号的时滞，求得控制器传递函数为：

利用平衡截断法降阶后控制器为：

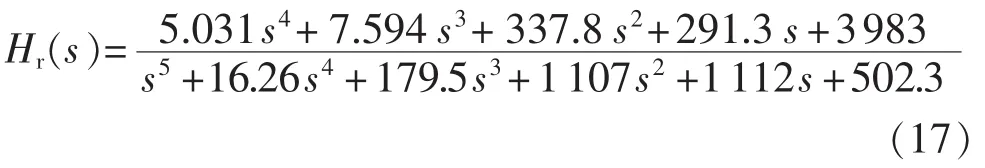
频率控制器降阶前后的Bode图如图4所示，在降阶前后控制器幅值、相角保持基本一致，满足要求。

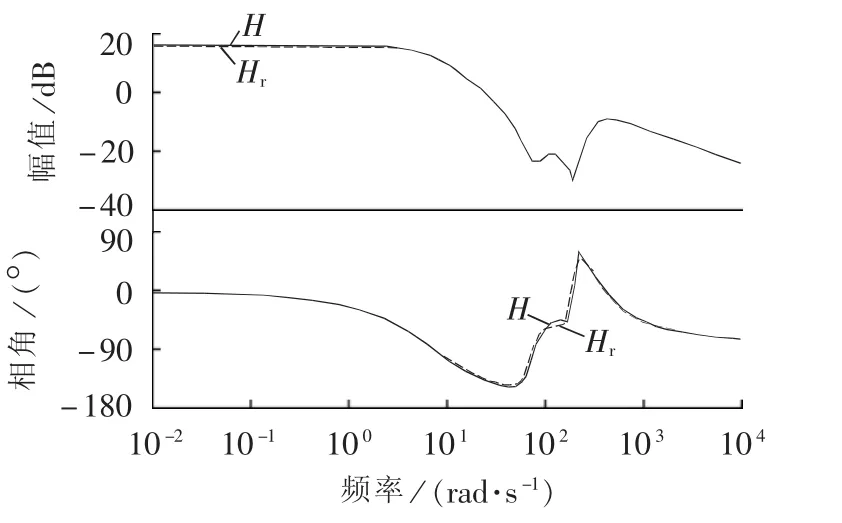
图4 控制器降阶前后Bode图Fig.4 Bode diagram of controller H and reduced-order controller Hr

4 仿真分析

首先将控制器Hr配置到图3设计的变结构频率附加控制器结构中，针对不同扰动在PSCAD／EMTDC中与根据根轨迹法设计的传统PI控制器进行对比仿真验证。

4.1 送端系统侧故障

扰动1：假设t=1s时，系统受某扰动导致整流侧定电流控制器的电流整定值上升至1.02 p.u.。分别配置不同控制器进行对比，控制效果如图5所示。

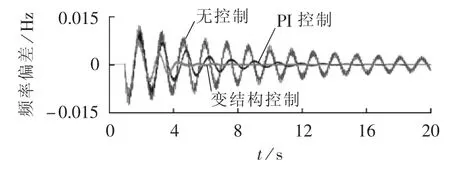
图5 扰动1下控制器配置前后频率偏差Fig.5 System frequency deviation before and after adding controller under first disturbance

由图5可见，当发生故障时引发系统频率出现振荡，分别配置2种控制器后，两者对频率振荡都具有良好的抑制效果，但PI控制明显不及变结构控制效果优良，使系统频率恢复稳定的时间较长，相比之下，变结构控制器具有更好的收敛性，能使频率更快地恢复稳定。

扰动2：假设t=1s时，在节点1与节点2之间的某一条交流线路靠近节点1侧的10%处发生0.1 s的三相短路接地瞬时故障。分别配置不同控制器进行对比，控制效果如图6所示。

图6 扰动2下控制器配置前后频率偏差Fig.6 System frequency deviation before and after adding controller under second disturbance

由图6可见，送端线路发生较严重的三相接地瞬时故障后，系统频率发生剧烈振荡，在2种控制器的分别作用下，都增强了系统的阻尼，但对比发现，PI控制对振荡抑制效果很有限，振荡后的前几个周期作用效果不明显，而变结构控制器能较快对振荡进行抑制，使频率偏差快速减小，系统频率迅速恢复稳定。

4.2 受端系统侧故障

扰动3：假设t=1 s时，系统逆变站至受端等值机线路的1%处发生0.1 s的三相短路接地的瞬时故障。分别配置不同控制器进行对比，控制效果如图7所示。

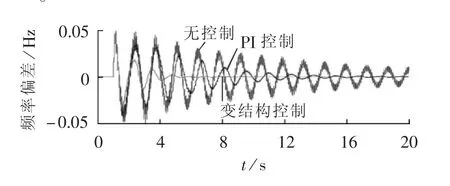
图7 扰动3下控制器配置前后频率偏差Fig.7 System frequency deviation before and after adding controller under third disturbance

由图7可见，当受端发生故障后，将引起送端系统频率发生较大振荡，配置不同控制器分别进行控制对比，发现系统频率振荡都得到抑制，但PI控制效果不理想，频率偏差收敛速度较慢，而变结构控制能较快使系统频率恢复正常。

由上述不同扰动仿真分析发现，当系统发生较大故障后，PI控制出现了控制不精确、效果不理想的情况，原因在于较大故障使得系统模型发生略大的变化，而PI控制是根据辨识出的线性模型设计的，易受系统扰动影响，从而控制周期长，抑制强度不明显；相反，基于变结构和PSO算法设计的频率附加控制器对系统的变化不敏感，在不同故障情况下，同样能提供良好的阻尼作用，快速减小频率振幅，对系统频率振荡都能进行有效控制，使系统频率快速恢复稳定，具有较强的鲁棒性。

4.3 PSO算法改进前后对比

为对比基本PSO算法和改进PSO算法的控制效果，特选取较严重故障扰动2进行对比分析，控制效果如图8所示。可以看出，通过对PSO算法中粒子的位置权重系数和惯性权重进行改进能有效提高控制器参数寻优的效率与精度，且提高了控制器的抑制效果，使系统频率更快恢复稳定。

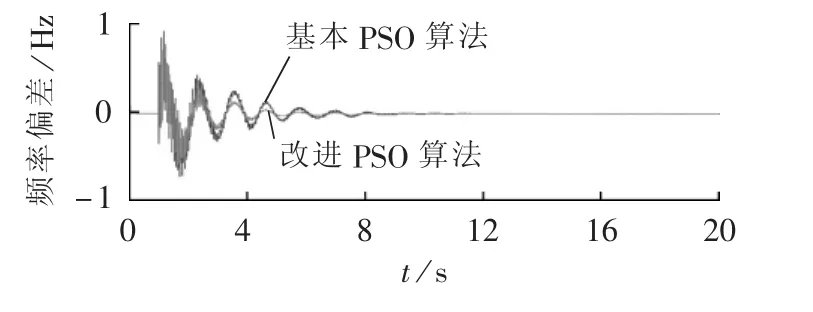
图8 扰动2下基本PSO算法和改进PSO算法的频率偏差Fig.8 System frequency deviation with traditional and improved PSO algorithms under second disturbance

5 结论

基于二次最优型变结构控制理论设计了HVDC附加频率控制器，并且将变结构控制器参数优化问题转化为极大极小值问题，进而提出一种改进PSO算法对参数进行优化。所提出的改进PSO算法收敛速度快且不易陷入局部最优，可有效提高控制器参数寻优的效率与精度。算例仿真结果表明，所设计的变结构HVDC附加频率控制器能有效抑制系统频率振荡，且具有较强的鲁棒性。

参考文献：

［1］梁旭明，张平，常勇．高压直流输电技术现状及发展前景［J］．电网技术，2012，36（4）：1-9．LIANG Xuming，ZHANG Ping，CHANG Yong．Recent advances in high-voltage direct-current power transmission and its developing potential［J］．Power System Technology，2012，36（4）：1-9．

［2］徐政．交直流电力系统动态行为分析［M］．北京：机械工业出版社，2004：4-7．

［3］KUNDER P．Power system stability and control［M］．New York，USA：McGraw-Hill，1994：13-25．

［4］宋墩文，杨学涛，丁巧林，等．大规模互联电网低频振荡分析与控制方法综述［J］．电网技术，2011，35（10）：22-28．SONG Dunwen，YANG Xuetao，DING Qiaolin，et al．A survey on analysis on low frequency oscillation in large-scale interconnected power grid and its control measures［J］．Power System Technology，2011，35（10）：22-28.

［5］李兴源，赵睿，刘天琪，等．传统高压直流输电系稳定性分析和控制综述［J］．电工技术学报，2013，28（10）：288-300．LI Xingyuan，ZHAO Rui，LIU Tianqi，et al．Research of conventional high voltage direct current transmission system stability analysis and control［J］．Transactions of China Electrotechnical Society，2013，28（10）：288-300．

［6］陈亦平，程哲，张昆，等．高压直流输电系统孤岛运行调频策略［J］．中国电机工程学报，2013，33（4）：96-102．CHEN Yiping，CHENG Zhe，ZHANG Kun，et al．Frequency regulation strategy for islanding operation of HVDC［J］．Proceedings of the CSEE，2013，33（4）：96-102．

［7］赵良，覃琴，郭强，等．中蒙直流输电工程送端孤岛频率控制问题［J］．电网技术，2008，32（21）：22-25．ZHAO Liang，QIN Qin，GUO Qiang，et al．Frequency control for islanded system at sending terminal of HVDC power transmission from ChinatoMongolia［J］．PowerSystem Technology，2008，32（21）：22-25．

［8］朱红萍，罗隆福．直流调制策略改善交直流混联系统的频率稳定性研究［J］．中国电机工程学报，2012，32（16）：36-43．ZHU Hongping，LUO Longfu．Improving frequency stability of parallel AC-DC hybrid systems by power modulation strategy of HVDC link［J］．Proceedings of the CSEE，2012，32（16）：36-43．

［9］马玉龙，石岩，殷威扬，等．HVDC送端孤岛运行方式的附加控制策略［J］．电网技术，2006，30（24）：22-25．MA Yulong，SHIYan，YIN Weiyang，etal．Additionalcontrol strategy for islanded AC system at sending terminal of HVDC［J］．Power System Technology，2006，30（24）：22-25．

［10］江全元，程时杰，曹一家．基于遗传算法的HVDC附加次同步阻尼控制器的设计［J］．中国电机工程学报，2002，22（11）：87-91．JIANG Quanyuan，CHENG Shijie，CAO Yijia．Design of HVDC supplementary subsynchronous damping controller using genetic algorithms［J］．Proceedings of the CSEE，2002，22（11）：87-91．

［11］李宽，李兴源，李保宏，等．基于射影定理分层控制的次同步阻尼控制器设计［J］．电力自动化设备，2015，35（2）：80-84．LI Kuan，LI Xingyuan，LI Baohong，et al．Design of supplementary subsynchronous damping controller based on projective theorem for hierarchical control［J］．Electric Power Automation Equipment，2015，35（2）：80-84．

［12］高为炳．变结构控制理论基础［M］．北京：科学出版社，1990：26-28．

［13］吴维鑫，王奔，李慧，等．电压源换流器高压直流输电系统的精确线性化变结构控制器设计［J］．电网技术，2011，35（7）：161-166．WU Weixin，WANG Ben，LI Hui，et al．Design of exact linearized variable-structure controller for VSC-HVDC power transmission system［J］．Power system Technology，2011，35（7）：161-166．

［14］OGATA K．Modern control engineering［M］．Upper Saddle River，New Jersey，USA：Prentice Hall，2010：311-342．

［15］杨帆，阮阳，袁荣湘．基于输出反馈的同步发电机非线性鲁棒励磁控制［J］．电力自动化设备，2012，32（10）：65-71．YANG Fan，RUAN Yang，YUAN Rongxiang．Nonlinerobust excitation control based on output feedback for synchronous generator［J］．Electric Power Automation Equipment，2012，32（10）：65-71．

［16］夏长亮，刘均华，俞卫，等．基于扩张状态观测器的永磁无刷直流电机滑模变结构控制［J］．中国电机工程学报，2006，26（20）：139-143．XIA Changliang，LIU Junhua，YU Wei，et al．Variable structure control of BLDCM based on extended state observer［J］．Proceedings of the CSEE，2006，26（20）：139-143．

［17］顾威，李兴源，王渝红，等．基于改进粒子群算法的次同步阻尼控制器设计［J］．电网技术，2010，34（8）：52-56．GU Wei，LI Xingyuan，WANG Yuhong，et al．Design of subsynchronousdamping controllerbased on improved particle swarm optimization algorithm［J］．Power System Technology，2010，34（8）：52-56．

［18］魏亮，王渝红，李兴源，等.高压直流输电送端孤岛运行附加频率控制器设计［J］. 电力自动化设备，2016，36（1）：143-148.WEI Liang，WANG Yuhong，LI Xingyuan，et al．Design of additional frequency controller for islanded sending-end operation of HVDC system［J］．Electric Power Automation Equipment，2016，36（1）：143-148．

［19］TRIPATHY P，SRIVASTAVA S C，SINGH S N．A modified TLS-ESPRIT-based method for low-frequency mode identification in power systems utilizing synchrophasor measurements［J］．IEEE Transactions on Power Systems，2011，26（2）：719-727．

［20］ZHANG Y，BOSE A．Design of wide-area damping controllers for interarea oscillations［J］．IEEE Transactions on Power Systems，2008，23（3）：1136-1143．