单相开路故障下五相直流无刷电机无位置传感器控制

田 兵，安群涛，段建东，孙 力，赵 克

（哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001）

0 引言

五相永磁同步电机的突出优点之一是容错运行，开路故障下，其可维持剩余相的相电流形成圆形磁势旋转即可保证五相电机无扰运行。通常当三相交流电机发生开路故障时，需构造三相四开关容错拓扑；而五相电机由于有较多的相自由度，实现容错控制非常方便，控制剩余相的相电流即可实现无扰运行［1-3］。

对于五相电机容错控制策略，大多数文献研究如何重构剩余相的相电流，以达到电磁转矩平稳输出的目的。如通过附加约束条件最小铜损损耗控制、相电流等幅值控制、转矩纹波最小控制等，可计算出上述代价函数下的最优相电流解［4-6］。大多数文献在计算开路故障下的相电流配置时需依赖电机模型参数，因此常采用离线计算方法重构相电流，同时采用电流滞环控制策略驱动故障电机［5-8］。但也有采用在旋转坐标系下重构电流的方法，如文献［9］提出了一种降阶Clarke和Park变换矩阵，实现了电流在同步旋转坐标系下的重新配置。这种方法可以实现故障电流的在线分配，然而由于所提出的Clarke和Park变换矩阵并未实现故障电机模型解耦，因此不宜采用旋转PI电流调节器控制故障电机。为此，文献［10］提出一种Clarke和Park变换矩阵，该变换矩阵不仅实现了dq坐标系下的故障电流重构，而且实现了故障电机在旋转坐标系下的解耦控制。

无位置传感器技术在三相交流电机中获得了广泛的应用，在中高速场合常采用基于基频模型的方法观测反电动势或磁链［11-13］；而当电机转速较低时，反电动势变得非常微弱，因此采用基于凸极追踪的无模型转子位置估算方法，如高频注入法。另外，文献［14］采用基于直接转矩控制的无位置控制方法，直接转矩实现只需估算转子初始角度，进而通过积分运算获取实时的αβ轴磁链和电磁转矩，通过直接控制转矩实现电机高动态品质控制，但采用无位置控制会引入较大的积分误差。滑模观测器／控制器对建模不确定性具有较好的抑制能力［15］，且算法简单易于数字实现，因此它在三相电机无位置控制中占主导地位［16-18］。近年来，由于出色的容错性能，多相电机获得广泛关注，然而传感器故障是多相电机运行时的一种常见故障类型。为了增强多相电机驱动系统的可靠性，文献［19］将基于滑模观测器的无位置控制技术应用于多相电机，采用随转速自适应变化的低通滤波器对观测反电动势进行平滑滤波。五相电机和传统三相电机的矢量控制在基波子平面具有较大的相似性，因此文献［19］提出的无位置传感器可方便地应用于五相电机并获得了成功。当五相电机出现开路故障时，由于缺乏有效的故障电机空间位置解耦模型，故障电机无位置控制技术发展缓慢。

本文根据文献［10］提出的故障电机解耦模型，实现单相开路运行模式下五相永磁同步电机的无位置控制技术。五相永磁无刷直流电机反电动势呈平顶波，其三次谐波气隙磁链将造成转速／转矩出现一定程度的波动，这在一定程度上降低了无位置传感器技术的控制精度［2，10］。 此外，考虑到故障电机运行过程参数摄动(如温度和磁饱引起电机磁阻的变化）以及建模的不确定性，本文通过滑模变结构观测器估算反电动势，并采用复系数滤波器提高估算反电动势信噪比。

复系数滤波器广泛应用于无线电通信及网侧变流器调节控制，然而其在电机调速系统中的应用并不常见［20-23］。文献［20］将复系数滤波器用于锁相环中，抑制网侧电压负序扰动，提高了网侧电压相位跟踪精度。文献［21］采用复系数比例谐振控制器在αβ平面对微电网逆变器的电压环进行控制。基于滑模观测器的反电动势估算方法需要自适应滤波器对其进行平滑滤波，以消除滑模抖振现象和非线性因素引起的谐波干扰。但由于二阶自适应带通滤波器数字实现较为繁琐［22-24］，且其动态性能难以满足实时性要求，故易引起无位置控制自激振荡。针对这种情况，本文提出一种一阶自适应复系数滤波器对估算反电动势进行平滑滤波。一阶自适应滤波器具备良好的动态性能、频率选择和极性选择等，其数字实现较为简单。它有针对性地提取正序分量而有效衰减负序分量。尽管五相电机在开路故障下基波电感和反电动势可实现较好的位置角度解耦变换，然而受建模不确定性的影响（主要是三次谐波绕组的影响），用场定向控制（FOC）时仍会造成观测反电动存在较强的抖震。

本文采用自适应复系数滤波器滤除谐波分量，提高位置辨识精度，并用得到的转子角度驱动故障电机。通过有限元分析分析了三次谐波绕组的影响，并通过实验验证了开路故障下无位置传感器技术的可行性，及所提位置辨识精度改善方法的有效性。

1 单相开路故障下五相电机模型

1.1 单相开路故障下的解耦模型

文献［10］提出了一种适用于单相开路运行模式下的Clarke和Park变换矩阵，其实现了基频旋转坐标系下电感和磁链矩阵的位置解耦变换，因而非常适合采用同步旋转PI调节器进行FOC。解耦变换矩阵是通过控制剩余相的电流维持定子励磁磁动势不变和反电动势不变而得到的，具体如式（1）、（2）所示［10］，其是实现故障电机解耦控制的关键。

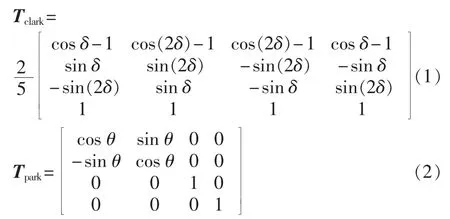
根据文献［10］，解耦变换后的电压方程如式（3）所示。

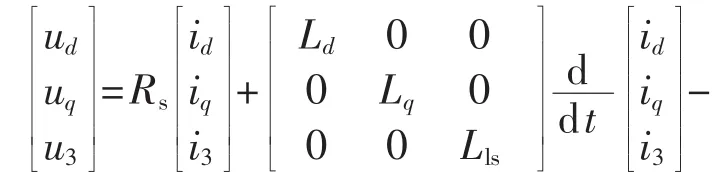
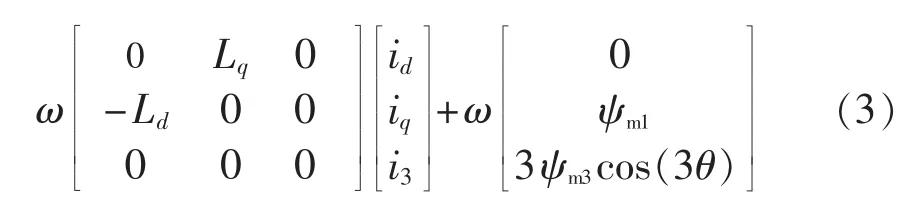
其中，id、iq分别为基频旋转坐标系下 d、q轴电流，i3为3倍频旋转坐标系下的脉振电流；Ld、Lq分别为同步旋转坐标系下 d、q 轴电感；Lls为漏电感；ψm1、ψm3分别为与相绕组交链的永磁体磁链的基波成分、3次谐波成分。 Ld=Lls+2.5（Lm-Lθ），Lq=Lls+2.5（Lm+Lθ），Lm和Lθ均为定值，其表达式可参见文献［9］，这表明故障电机在新的旋转空间下交直轴电感与电机正常模式完全相同。

通过解磁共能对位置求偏导，可得转矩方程如下：

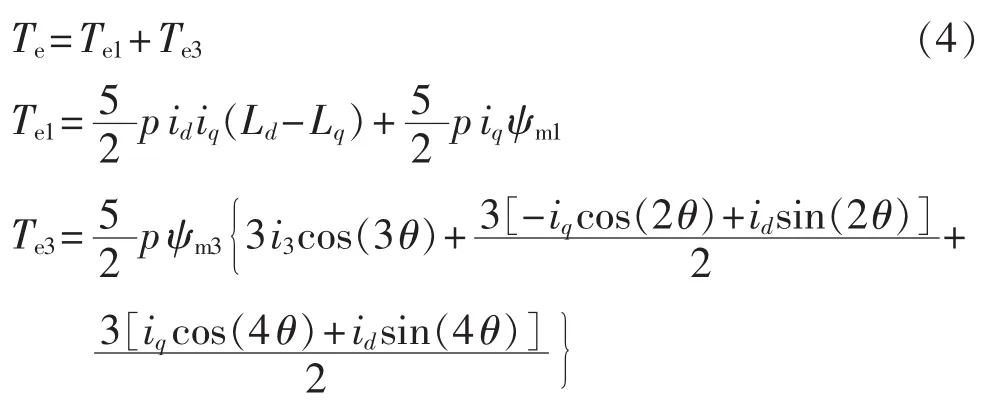
其中，Te、Te1和Te3分别为总电磁转矩、平均电磁转矩和谐波电磁转矩；p为电机极对数。从电磁转矩表达式可以看出，由于3次谐波的存在，电磁转矩将出现2倍频和4倍频脉动，因此采用正弦波绕组电机可从根本上消除故障电机的转矩脉振。同时由转矩方程可以看出，对于开路故障下的五相电机控制可以采用弱磁控制以达到增加输出转矩的目的，然而此时由于id≠0，转矩脉动也变得较大。因此采用id=0控制，有利于平滑输出转矩，它是一种简单有效的故障电机驱动控制方案。本文采用id=0控制，并在此基础上实现无位置电机驱动控制。

1.2 相电流等幅值控制驱动故障电机

为充分利用变频器的容量，对容错电流进行控制时，采用电流等幅值控制。此时，可通过附加约束条件ib=-id，ic=-ie求解故障电机的相电流。

结合以上约束条件，根据文献［10］，当采用id=0，iq=C（C为常数），即采用定子磁动势不变原则控制故障电机时，dq坐标系下的容错电流配置表达式为：

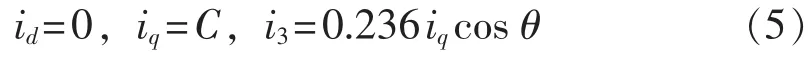
在自然坐标系下可以表示为：

由式（6）可以看出，等幅值的电流转换到旋转坐标系下基本实现了基波空间解耦，控制i3=0.236iqcos θ是实现电流等幅值控制的关键。

此时电磁转矩为：

2 单相开路故障下的无位置传感器技术

单相开路故障下的五相电机可采用电流滞环控制，具有稳态精度高、动态响应快、控制简单等优点，然而由于其开关频率具有不固定特性，使之难以适用于大功率场合。本文所采用的五相电机容错模型在基频旋转空间解耦得较为彻底，可采用FOC及脉宽调制技术。因此在同步旋转空间中，可以方便地应用无位置传感器。但必须注意以下2点：由于3次谐波绕组的存在，电机实际运行参数如交直轴电感并非恒定，而是会出现一定量的2倍频和4倍频的波动，用无位置传感器技术应能抑制这些建模不确定性因素；由于3次谐波绕组的存在，当采用恒定iq电流控制时，转矩特性不能做到完全平直，而是会出现2倍频和4倍频的波动。这种电磁转矩波动会导致反馈的位置信息出现波动，因此有必要采取有效的滤波器对观测反电动势进行滤波。基于以上考虑，本文采用基于滑模观测器的位置估算方法，结合一种改进复系数滤波器对观测反电动势进行平滑滤波。

2.1 基于滑模观测器的反电动势估算

从式（3）可以看出，开路故障下五相电机的电流和转速控制完全可以媲美三相电机矢量控制。在新的旋转坐标系下，故障电机的基波空间和3次谐波空间可实现解耦。因此仅考虑基波空间，故障电机在dq坐标系下可以表示为：

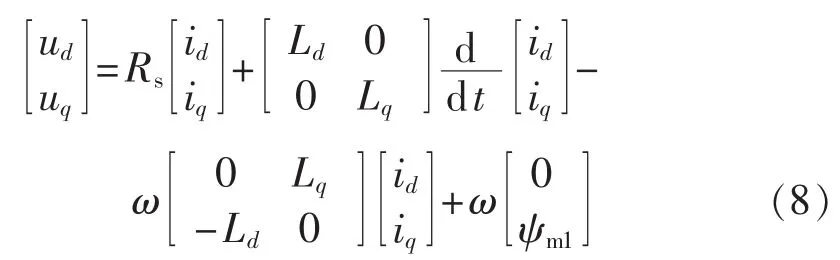
类似于三相交流电机，可采用扩展反电动势表示以上模型。此时，具有空间凸极效应的电机（转子结构凸极或磁饱和凸极）可以表示为：

其中，Eex为扩展反电动势。

电压方程在αβ平面可表示为：

其中，下标“α”、“β”分别表示相应量在 α、β 轴下的分量；eα和eβ为扩展反电动势在αβ平面上的投影。

采用状态空间表示电机电压方程如下：

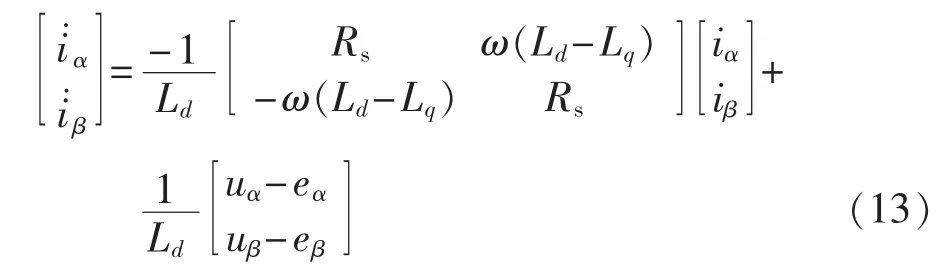
因此可构建基于二阶滑模观测器的无位置传感器，如图1所示。

图1 基于滑模观测器的无位置传感器原理图Fig.1 Principle diagram of position sensorless based on sliding mode observer

图1中，uα、uβ为输入端电压；为电流状态观测器输出；zα、zβ为滑模观测器输出，并且是抖震的。经滤波器移除zα、zβ中的谐波分量，便可得到平滑的观测反电动势进而采用锁相环技术估算转子位置经锁相环估算的转子转速是存在纹波的，用一阶滤波器滤除脉动分量后得到较为平滑的转子转速，其中一阶滤波器的时间常数应和驱动系统的机械时间常数保持一致。

2.2 改进型复系数滤波器

采用滑模观测器估算的反电动势为基波反电动势。实际驱动系统存在2倍频和4倍频脉动，电流环采用PI调节器时，因交直轴电感存在波动电感而产生的谐波电流不能被PI调节器抑制。因此PI调节器输出，也就是电机端电压 uα、uβ会出现脉动。 uα、uβ作为滑模观测器的输入，会导致观测反电动势产生强烈的抖震现象。由于观测反电动势含有较大的谐波，通过滤波器滤除谐波，可得到正弦反电动势。然而传统方法中采用低通滤波器将引起估算反电动势相位滞后，使估算的转子位置出现一定的偏差。因此本文引入一种复系数滤波器，这种滤波器计算量小，且具备良好的动态响应性能。

复系数滤波器是实系数滤波器的中心频率（谐振频率）经移频而得的。实系数滤波器的频率特性相对于虚轴是对称的，即对于正频率和负频率有同样的增益。然而复系数滤波器关于虚轴是非对称的，因此它可以筛选出正序分量而有效抑制负序分量［18］。

以一阶惯性滤波器为例，有：

其中，ωc为截止频率。该一阶低通滤波器可以看作中心频率为0的一阶带通滤波器。将该滤波器的中心频率向虚轴右侧移频ωr，可得：

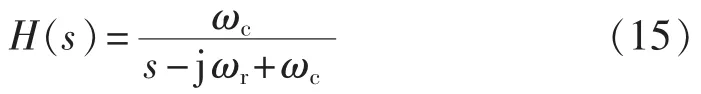
其中，ωr为一阶带通复系数滤波器的中心频率（谐振频率）。复系数滤波器的Bode图如图2所示。

图2 复系数滤波器Bode图Fig.2 Bode diagram of complex coefficient filter

图2为中心频率分别为-50、0、50 Hz的一阶复系数滤波器Bode图。图中，中心频率为0的复系数滤波器就是传统的一阶低通滤波器。可以看出，复系数滤波器在中心频率处，无幅值衰减，无相位滞后。因此完全可以采用复系数滤波器取代传统的一阶低通滤波器，对估算的反电动势进行平滑滤波。

交流电机调速系统反电动势的频率是变化的，因此复系数滤波器的中心频率（谐振频率）应能随转速做出相应的调整。假设电机逆时针旋转方向为正方向，当采用一阶复系数滤波器，对正向旋转的电机进行观测反电动势滤波时，对于α轴有：

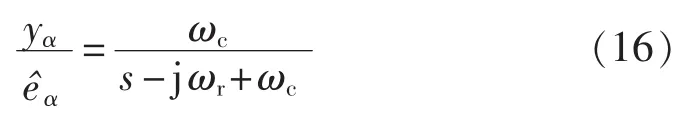
经变换得：

其中，yβ为β轴滤波器输出。由于观测反电动势不含有负序分量，因此可以认为β和yβ在基波成分上等效（等幅值、同相位）。 因此在式（17）中采用β取代yβ，这样可以改善复系数滤波器的动态响应，而β中的高频抖振则可以通过积分器滤除。

同理，对于β轴观测反电动势滤波有：

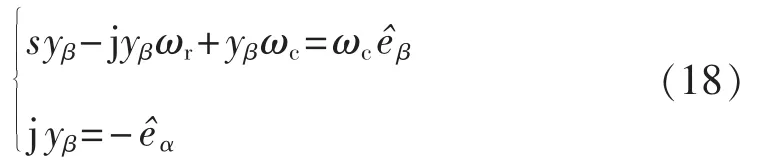
根据式（16）和（17），得到改进后的复系数滤波器传递函数框图如图3所示。

从图3中可以看出，一阶自适应复系数滤波器结构简单，可有效取代传统的一阶低通滤波器或二阶带通滤波器，且滤波后的反电动势无相位延迟和幅值衰减，因此从观测反电动势提取出的转子位置可近似认为是实际转子位置。

图3 改进后的复系数滤波器传递函数框图Fig.3 Transfer function block diagram of improved complex coefficient filter

3 故障电机建模不确定性分析

采用Maxwell／Ansoft软件对一台2对极、齿槽数为30的表贴式电机进行有限元分析。仿真模型为五相无刷直流电机，电机绕组分布如图4所示。电机反电动势呈梯形波，关键的电磁参数如下：基频磁链ψm1=0.515 482 5 Wb，三次谐波磁链 ψm3=0.024 718 Wb，直轴电感Ld=7.34 mH，交轴基频电感Lq=9.18 mH，漏电感Lls=1.74 mH。

图4 五相永磁无刷直流电机绕组分布图Fig.4 Winding configuration of five-phase BLDC motor

仿真时设置电机转速为900 r／min，通过有限元分析求解动态相电感和反电动势分别如图5和图6所示。为表述简洁，图5中仅标注了a相的自感以及a相与其他相的互感。

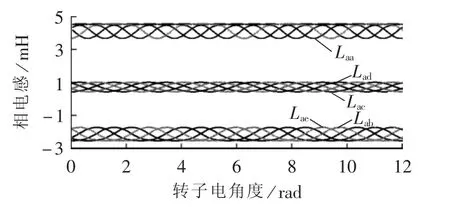
图5 五相永磁无刷直流电机相电感Fig.5 Phase inductances of five-phase BLDC motor

图6 五相永磁无刷直流电机反电动势Fig.6 Back-EMFs of five-phase BLDC motor

由图5和6可知，尽管仿真电机为表贴式同步电机，但由于磁饱和的原因，定子电感耦合了转子位置信息；反电动势为梯形波，表明有相当量的3次谐波绕组存在。

采用式（1）和（2）所示的变换矩阵，将转子位置耦合的相电感及相永磁体磁链转换到同步旋转坐标系下，得到dq坐标系下的动态电感和反电动势波形分别如图7和图8所示。可见，由于3次谐波绕组的分布，在dq坐标系下交直轴电感出现一定程度的波动，这些波动量占平均电感的1%～1.6%；谐波电感产生谐波电流，一定程度上引发观测反电动势抖振。考虑以上干扰因素，需要采用复系数滤波器平滑观测反电动势，进而优化无位置传感器技术的控制性能。

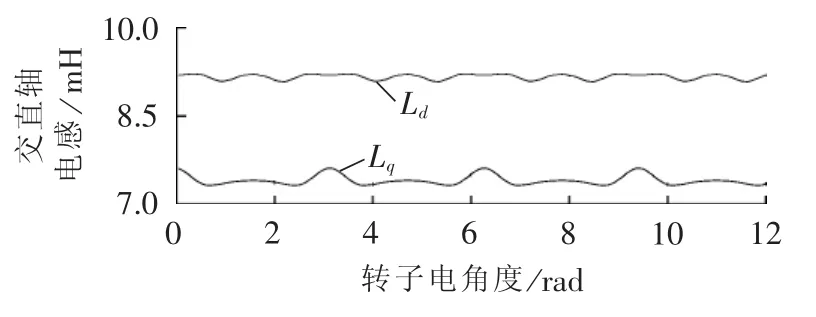
图7 单相开路模式下d、q轴电感Fig.7 d-and q-axis inductances under single-phase open circuit mode

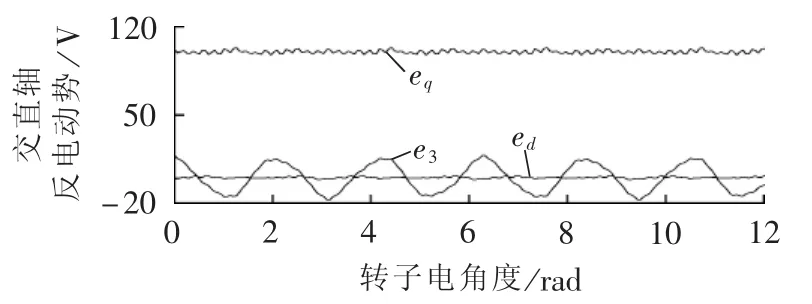
图8 单相开路模式d、q轴反电动势Fig.8 d-and q-axis back-EMFs under single-phase open circuit mode

4 实验分析

在3 kW五相电机驱动平台上，对单相开路模式下的无位置传感器技术进行验证。实验电机参数同第3节，采用五相半桥逆变器控制五相电机，直流电机作为负载。控制器采用DSP与FPGA相结合的模式，其中DSP完成控制算法（电流闭环控制、无位置控制等），FPGA完成Clarke和Park变换（包括逆变换）、脉宽调制。采样频率为5.15kHz，IGBT模块的开关频率为10.30 kHz，电机转动惯量为0.33 kg／m2。需要注意的是，由于转子轴上的转动惯量较大，驱动系统输出转速相当于经过了一阶惯性滤波器，因此电机转速波动有所改善。

4.1 单相开路模式FOC

图9为等幅值控制策略下剩余可控相的相电流波形。可见，由于采用FOC策略，相电流波形基本正弦，这表明引入解耦模型的正确性和有效性。

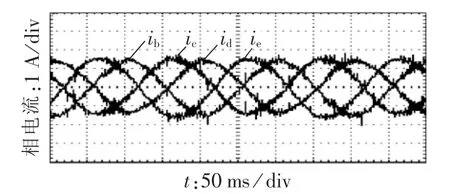
图9 等幅值控制下相电流波形Fig.9 Waveforms of phase current under equal magnitude control

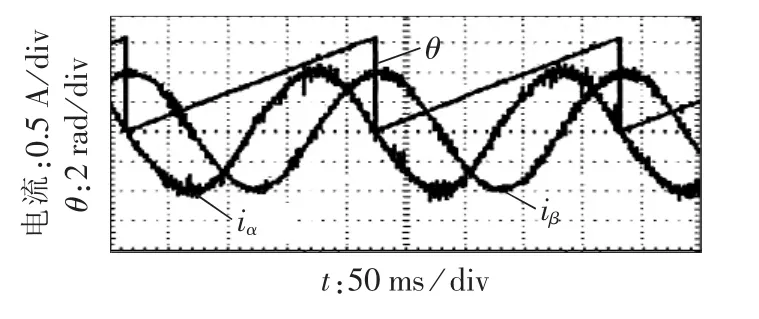
图10 等幅值控制下α、β轴电流波形Fig.10 Waveforms of α-and β-axis currents under equal magnitude control

图10为相电流等幅值控制下αβ坐标系下的电流。由图可知，α轴和β轴电流波形正弦且互相正交，它们形成圆形旋转定子磁动势维持机电能量平稳转换。同时从转子位置θ曲线可以看出，转速比较平稳，这是由于驱动系统转动惯量较大，对波动的电磁转矩实施了一次机械惯性滤波。

图11为相电流等幅值控制策略下αβ坐标系下的定子端电压。可以看出，uα、uβ并非纯正弦，而是含有相当量的谐波，这些谐波由3次谐波气隙磁链引起；采用相电流等幅值控制时，3次谐波空间电压也出现脉振。

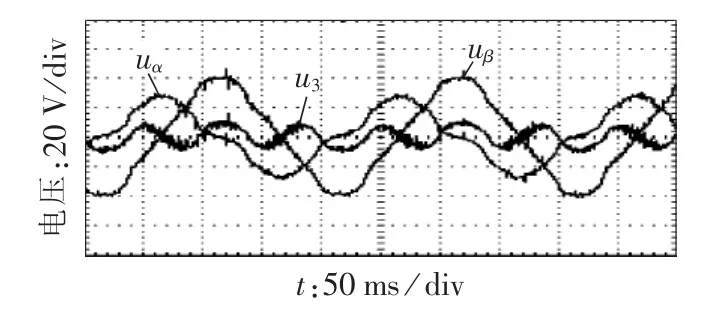
图11 等幅值控制下α、β轴定子输入端电压波形Fig.11 Waveforms of α-and β-axis stator terminal voltages under equal magnitude control

4.2 单相开路模式无位置控制

图12为观测反电动势经复系数滤波器滤波前后对比波形。由于自适应复系数滤波器中心频率和剪切频率可随转子转速同步变化，因此相对于抖振反电动势，滤波后电动势无相位和幅值失真。观测反电动势经锁相环，可得观测转子位置及转速。由图12可知，观测转子位置和实测位置一致性较好，这说明改进型复系数滤波器具有较好的稳态滤波效果。需要注意的是，此时控制电机的位置信号仍然由机械位置传感器给出。

图12 观测反电动势滤波前后对比Fig.12 Comparison of estimated back-EMFs before and after filtering

图13为无位置控制技术投入前后实测和观测转子位置、观测反电动势、转子位置观测误差波形。1.25 s前，电机由机械位置传感器控制，1.25 s时电机角度控制信号由观测转子位置信号替换，转子角度观测误差由0°变为最大5°（电角度）。可见，电机角度控制信号切换前后，电机运行平稳，这说明了改进型复系数滤波器具有较好的动态响应。

图13 无位置控制前后转子位置观测误差波形Fig.13 Waveforms of rotor position estimated error before and after sensorless control

图14为无位置控制电机时实测和观测转子转速、观测转子位置、转子位置观测误差波形。可见，单相开路故障模式下电机无位置驱动控制系统平稳运行，观测转子转速经一阶惯性滤波器滤波，其观测值和实测转速值一致性较高。

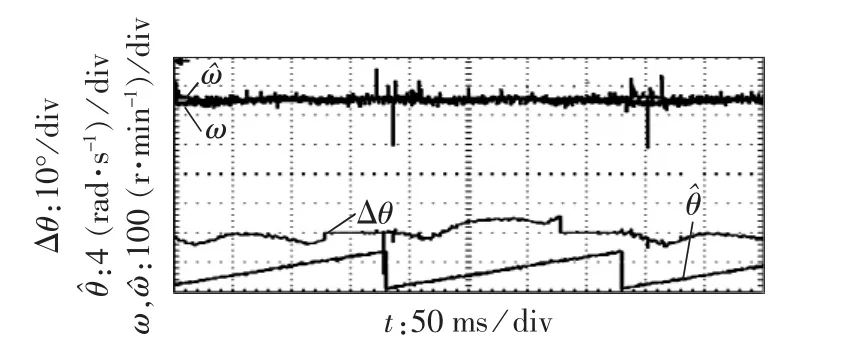
图14 无位置控制时观测和实测转速对比Fig.14 Comparison between estimated and true rotor speed with sensorless control

图15为采用无位置控制时交轴电流阶跃扰动下观测转子位置、观测基波反电动势、转子位置观测误差信号动态波形。可见，q轴电流从1 A阶跃到1.5 A，转子位置观测误差瞬态值高达44°，此时观测反电动势和观测转子位置亦出现较大的波动；经过滑模观测器1 s的跟踪调整，观测转子位置重新跟踪上实测位置位置，动态过程结束后观测转子观测误差保持在5°以内。

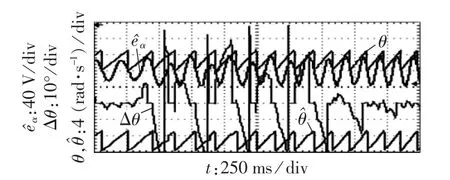
图15 q轴电流阶跃扰动下转子位置观测误差波形Fig.15 Waveforms of rotor position estimated error under q-axis current step change disturbance

图16为采用无位置控制时交轴电流阶跃扰动下观测和实测转子转速、观测转子位置、转子位置观测误差波形。观测转子转速采用一阶惯性滤波器滤波，且滤波时间常数和转子轴机械时间常数接近。由图可见，在阶跃扰动瞬间，观测转子转速和实际转速动态变化一致；动态过程结束后观测转子观测误差保持在5°以内，展示了良好的抗扰动效果。

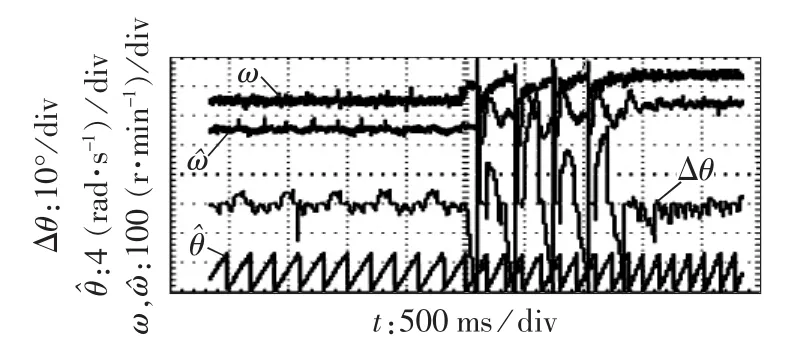
图16 q轴电流阶跃扰动下观测和实测转速对比Fig.16 Comparison between estimated and true rotor speed under q-axis current step change disturbance

5 结论

本文实现了五相永磁同步电机单相开路模式下无位置控制技术，并取得了如下成果：基于一种新颖的故障电机空间位置解耦模型，采用滑模观测器估算了转子位置并控制故障电机；提出一种简单有效的改进型自适应复系数滤波器，对观测反电动势进行无失真平滑滤波；实验结果显示转速低至150 r／min时无位置控制精度高达5°（电角度），且能适应q轴电流阶跃扰动。为了实现在全速域内的故障电机无位置控制，后续工作将开展基于高频注入法和基于直接转矩控制的无位置传感器技术的研究。相比于正常模式，故障电机的无位置控制难点在于存在较大的建模不确定性（如由于谐波绕组分布导致交直轴电感出现一定程度的波动），如何有效地提取转子位置信号是有别于采用三相电机无位置控制时的。

参考文献：

［1］GUZMAN H，DURAN M J，BARRERO F，etal．Comparative study of predictive and resonant controllers in fault-tolerant fivephase induction motor drives［J］．IEEE Transactions on Industrial Electronics，2016，63（1）：606-617．

［2］TIAN B，AN Q，DUAN J D，et al．Cancellation of torque ripples with FOC strategy under two phase failures of five-phase PM motor［J］．IEEE Transactions on Power Electronics，2017，32（7）：5459-5472．

［3］魏书荣，黄苏融，符杨，等.永磁同步电机及其驱动系统故障处理与容错机制研究综述［J］. 电力自动化设备，2016，36（10）：100-107.WEI Shurong，HUANG Surong，FU Yang，et al.Overview on fault disposal and fault-tolerance mechanism of PMSM and its driving system［J］.Electric Power Automation Equipment，2016，36（10）：100-107.

［4］SEDRINE E B，OJEDA J，GABSI M，et al．Fault-tolerant control using the GA optimization considering the reluctance torque of a five-phase flux switching machine［J］．IEEE Transactions on Energy Conversion，2015，30（3）：927-938．

［5］MOHAMMADPOUR A，SADEGHI S，PARSA L．A generalized faulttolerant control strategy for five-phase PM motor drives considering star，pentagon，and pentacle connections of stator windings［J］．IEEE Transactions on Industrial Electronics，2014，61 （1）：63-75．

［6］MOHAMMADPOUR A，PARSA L．A unified fault-tolerant current control approach for five-phase PM motors with trapezoidal back EMF under different stator winding connections［J］．IEEE Transactions on Power Electronics，2013，28（7）：3517-3527．

［7］LIU G，QU L，ZHAO W，et al．Comparison of two SVPWM control strategies of five-phase fault-tolerant permanent-magnet motor［J］．IEEE Transactions on Power Electronics，2016，31（9）：6621-6630．

［8］MOHAMMADPOUR A，PARSA L．Global fault-tolerant control technique for multiphase permanent-magnet machines［J］．IEEE Transactions on Industry Applications，2015，51（1）：178-186．

［9］HYUNG-MIN R，JI-WOONG K，SEUNG-KI S．Synchronous-frame current control of multiphase synchronous motor under asymmetric fault condition due to open phases［J］．IEEE Transactions on Industry Applications，2006，42（4）：1062-1070．

［10］TIAN Bing，AN Q，DUAN Jiandong，et al．Decoupled modeling and nonlinear speed control for five-phase PM motor under single phase open fault［J］．IEEE Transactions on Power Electronics，2017，32（7）：5473-5486．

［11］张晓光，孙力，陈小龙，等.基于二阶滑模观测器的永磁同步电机无位置传感器控制［J］. 电力自动化设备，2013，33（8）：36-41.ZHANG Xiaoguang，SUN Li，CHEN Xiaolong，et al.PMSM sensorless control based on second-order sliding mode observer［J］.Electric Power Automation Equipment，2013，33（8）：36-41.

［12］肖烨然，刘刚，宋欣达，等.基于改进滑模观测器的永磁同步电机无位置传感器 I／F起动方法［J］.电力自动化设备，2015，35（8）：95-102.XIAO Yeran，LIU Gang，SONG Xinda，etal.SensorlessI／F startup based on modified sliding mode observer for PMSM［J］.Electric Power Automation Equipment，2015，35（8）：95-102.

［13］王要强，马小勇，程志平，等.PMSM转子初始位置检测分析及起动策略［J］. 电力自动化设备，2016，36（9）：156-161，168.WANG Yaoqiang，MA Xiaoyong，CHENG Zhiping，et al.Power system cascading failure model based on complex network theory with consideration of corrective control ［J］.Electric Power Automation Equipment，2016，36（9）：156-161，168.

［14］ZHENG L，FLETCHER J E，WILLIAMS B W，et al．A novel direct torque control scheme for a sensorless five-phase induction motor drive［J］．IEEE Transactions on Industrial Electronics，2011，58（2）：503-513．

［15］邹延生，董萍.基于协同控制理论的非线性直流附加控制器设计［J］. 电力自动化设备，2017，37（4）：210-217.ZOU Yansheng，DONG Ping.Design of nonlinear HVDC supplementary controller based on synergetic control［J］.Electric Power Automation Equipment，2017，37（4）：210-217.

［16］张晓光，姜云蜂，赵克，等.高速永磁同步电机滑模变结构一体化解耦控制［J］. 电力自动化设备，2013，33（6）：58-63.ZHANG Xiaoguang，JIANG Yunfeng，ZHAO Ke，et al.Slidingmode variable-structure control of high-speed PMSM based on precision linearization control［J］.Electric Power Automation Equipment，2013，33（6）：58-63.

［17］戴卫力，丁骏，田浩，等.双凸极电励磁发电机系统非奇异终端滑模控制器的设计与仿真［J］. 电力自动化设备，2015，35（6）：130-135.DAI Weili，DING Jun，TIAN Hao，et al.Design and simulation ofnonsingularterminalsliding mode controllerfordoubly salient electromagnetic generator system［J］.Electric Power Automation Equipment，2015，35（6）：130-135.

［18］LI W，FANG J，LI H，et al.Position sensorless control without phase shifter for high-speed BLDC motors with low inductance and nonideal back EMF［J］．IEEE Transactions on Power Electronics，2016，31（2）：1354-1366．

［19］程帅，姜海博，黄进，等.基于滑模观测器的单绕组多相无轴承电机无位置传感器控制［J］. 电工技术学报，2012，27（7）：71-77.CHENG Shuai，JIANG Haibo，HUANG Jin，et al.Position sensorless control based on sliding mode observer for multiphase bearingless motor with single set of windings［J］.Transactions of China Electrotechnical Society，2012，27（7）：71-77.

［20］谢门喜，朱灿焰，杨勇.应用复系数滤波器的不平衡电网电压锁相方法［J］. 电气工程学报，2016，11（8）：37-41.XIE Menxi，ZHU Canyan，YANG Yong.Synchronous reference frame PLL with complex coefficient filter under unbalanced three-phase system［J］.Journal of Electrical Enginnering，2016，11（8）：37-41.

［21］曾正，邵伟华，李辉，等.孤岛微网中虚拟同步发电机不平衡电压控制［J］. 中国电机工程学报，2017，37（2）：372-381.ZENG Zheng，SHAO Weihua，LI Hui，et al.Unbalanced voltage control of virtual synchronous generator in islanded micro-grid［J］.Proceedings of the CSEE，2017，37（2）：372-381.

［22］杨文韬，耿华，肖帅，等.大型风电机组的比例-积分-谐振独立变桨距控制策略［J］. 电力自动化设备，2017，37（1）：87-92.YANG Wentao，GENG Hua，XIAO Shuai，et al.PI-R individual pitch control for large-scale wind turbine［J］.Electric Power Automation Equipment，2017，37（1）：87-92.

［23］任佳佳，胡应宏，纪延超.基于αβ坐标系下双馈异步风力发电机串补输电系统次同步谐振的比例谐振控制［J］.电力自动化设备，2017，37（9）：1-5.REN Jiajia，HU Yinghong，JI Yanchao.PR control of sub-synchronous resonance in DFIG connected to series com-pensated power transmission system based on αβ axis［J］.Elec-tric Power Automation Equipment，2017，37（9）：1-5.

［24］ZHANG G，WANG G，XU D，etal.ADALINE-network-based PLL for position sensorless interior permanent magnet synchronous motor drives［J］.IEEE Transactions on Power Electronics，2016，31（2）：1450-1460.