海上风机一体化电磁暂态模型与雷电暂态过电压研究

王国政 ，张 黎 ，吴 昊 ，赵 彤 ，邹 亮

（1.山东大学 电气工程学院，山东 济南 250061；2.山东大学 山东省特高压输变电技术与装备重点实验室，山东 济南 250061）

0 引言

在能源问题日益严峻的形势下，风能逐步成为当今世界上发展最为迅速、应用最为广泛的可再生能源［1-3］。风机作为风能资源开发利用的直接载体，随着风电场的海洋化及大容量发电机组的投入使用，风机的高度越来越高。再加之海洋环境潮湿多雨、接地环境复杂、雷暴现象频繁，使得海上风机遭受雷击的概率大幅增加。根据国际电工委员会统计的实际运行情况显示，在雷暴活动频繁的区域由雷击造成风机的损坏率高达14%。风机是风电场中最贵重的组成部分，其成本超过风电工程总投资的60%。雷击不仅会造成风机本身损坏，严重时还会造成风电场停运，甚至威胁到电网的安全运行［4］。因此海上风机的雷击防护已经成为目前亟需解决的重大技术问题。

风机遭受雷电袭击时，携带巨大能量的雷电流一般会在机组桨叶顶端的接闪器（或机舱尾部的避雷针）注入，由桨叶内部布设的金属导体引流，再经机舱的导流路径进入塔体顶端，经过塔体进入风机的接地装置，最终泄流进入大地。雷电流在整个泄流的暂态过程中，会导致风机各部位出现电位跃升现象，可能对设备造成反击或绝缘损坏［5］。机舱处存在电力系统和控制系统等大量电气设备，对其过电压的防护显得尤为重要。

目前国内外学者对风机防雷性能的研究主要有实验研究和理论分析2种。在实验研究方面，日本科学家Kazuo Yamamoto［6］按照实际风机进行缩比搭建风机模型，并用电极模拟雷电发生器完成了雷击模拟实验，分析塔筒底部地电位升。但由于实验研究耗资巨大［7］，实验模型可移植性不灵活，以及实验电源难以模拟雷电既是电压源又是电流源的双重特性，与实际风机的等效性有待进一步考证，所以现有针对雷击风机特性的研究以计算机理论分析为主。在理论分析方面，清华大学张波教授［8-9］利用矩量法探讨了风机接地装置电位升的影响因素；文献［10-12］利用时域有限差分（FDTD）法对风机环形接地极进行分析；文献［13］考虑塔筒与传输线间杂散电容的影响，分析了塔筒内部传输线的感应过电压。虽然现有针对风机的雷电暂态响应已有较多研究，但都以陆上风机为主，没有考虑海洋因素尤其是海水层对风机暂态电位的影响，且专门针对机舱处暂态电位的研究较少。另外多数风机建模一般采用传统的经验公式［14-15］，不能体现叶片旋转角度对波阻抗模型的影响。

本文首先结合海洋接地环境的分层特性，建立了海上风机接地模型，提出了海上风机冲击接地电阻数值计算方法；根据海上风机桨叶旋转特性和圆锥天线理论，分别建立了桨叶和塔筒的波阻抗模型；在波阻抗模型基础上搭建了雷击风机的ATP-EMTP仿真模型，并与传统的波阻抗模型进行比较；分析了海水深度、桨叶和塔体长度、雷电流参数、雷击点和桨叶旋转位置对机舱处暂态过电压的影响。这对海上风机防雷系统的设计具有一定的指导意义。

1 海上风机雷电暂态效应计算模型

当海上风机遭受雷击时，雷电流在风机上会形成一定的流通路径，通常是经过风机桨叶、塔筒向下传导至接地装置。要准确地分析风机体上暂态过电压的情况，需要准确地建立风机各部位的计算模型。

1.1 海上风机冲击接地电阻数值计算

海上风机的接地系统设计与传统的陆上风机存在着较大差别。海上风机普遍采用导管架基础，考虑到经济性和施工的难易程度，一般工程上利用基础作为自然接地体。目前海上风机的基础形式具体可细分为单桩式基础、重力式基础、吸力式基础、多桩式基础和漂浮 式 基 础［16］。其 中，目前应用最为广泛的是单桩式基础，其结构示意图见图1。

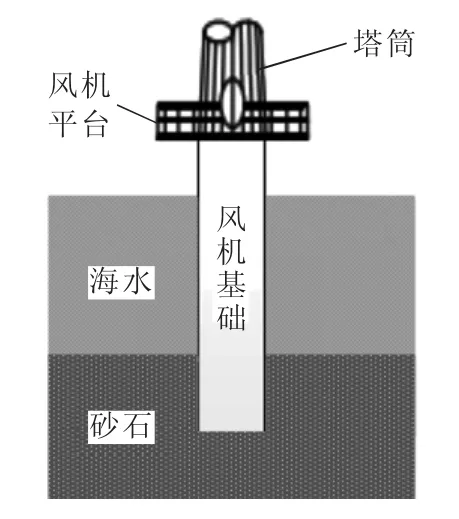
图1 单桩式海上风机基础示意图Fig.1 Schematic diagram of single piled foundation of offshore wind turbine

接地电阻的计算采用土壤中点电流源格林函数求解，利用傅里叶变换、分离变量法［17］求解圆柱坐标系下的拉普拉斯方程，获得土壤中点电流源的电位函数为：

其中，φ（λ）和 γ（λ）为待定系数；J0（λr′）为第一类零阶Bessel函数；λ为任意常数；r′为圆柱坐标系下的径向距离。

由于海上风机接地环境分为海水层和土壤层，接地体被分成上、下2段圆柱体，需要分别进行电位函 数计 算［18］。海上风机接地示意图如图2所示。图中，l为接地体总长度；a为基础半径；h1为上层海水深度；ρ1为上层海水电阻率；ρ2为下层海床砂石电阻率。可得到上层海水和下层土壤中接地体部分的电流密度分别为δ1与 δ2，其关系如式（2）所示。

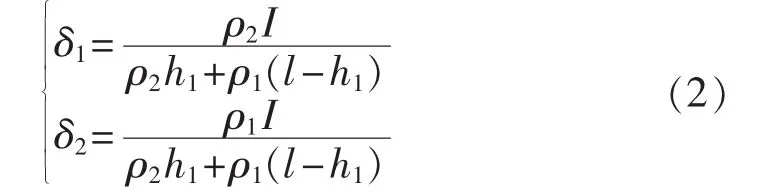
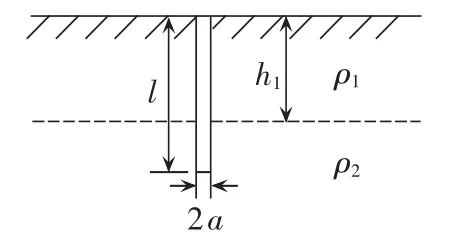
图2 海上风机接地示意图Fig.2 Grounding diagram of offshore wind turbine

其中，I为进入接地极的总电流。

利用式（1）、式（2）可分别求出上层海水、下层土壤的电位函数φδ1、φδ2。由叠加原理可得到海洋双层接地环境下单桩式风机的冲击接地电阻数值表达式为：

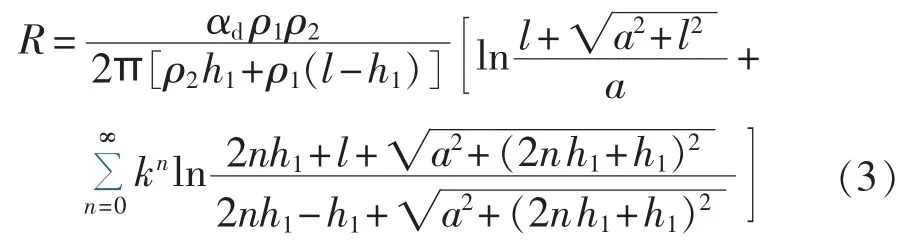
其中，k=（ρ2-ρ1）／（ρ2+ρ1）；αd为冲击系数，考虑到单桩式基础为垂直筒状，其半径远远大于普通接地装置中扁钢的半径，接地体周围火花放电现象不明显［19］，αd可取近似值1。

1.2 考虑旋转因素的桨叶波阻抗建模

桨叶的旋转会使桨叶的电容、电感等参数发生改变，由波阻抗定义式可知桨叶波阻抗也会随之发生变化，这种变化随着桨叶长度的增加愈加明显。因此，要准确地建立桨叶波阻抗模型，就要同时考虑旋转角度、塔筒高度和桨叶长度的影响。由于海水导电性良好，可将海面视为良导体，计算时风机及其关于海面的镜像如图3所示。图中，l1、l2、l3和h分别为风机3片桨叶长度和塔筒高度；l′1、l′2、l′3和 h′分别为风机桨叶和塔筒关于海面的镜像。

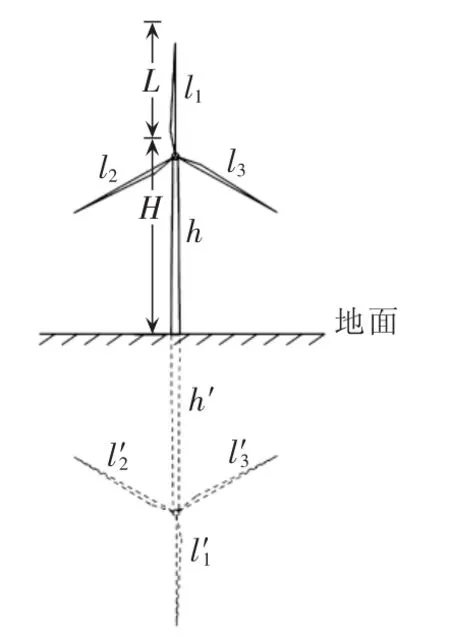
图3 风机及其镜像示意图Fig.3 Schematic diagram of wind turbine and its mirror image

采用平均电位法计算桨叶电容。考虑到海上风机高度远大于塔筒半径，故可忽略塔筒半径的影响，假设桨叶和塔筒均匀带电且电荷都集中在轴线上，其电荷线密度为τ。根据图3所示的几何关系可以求得桨叶对地电容Cg、桨叶对塔筒电容Clh和桨叶间电容 Cl1／2，分别如式（4）—（6）所示。

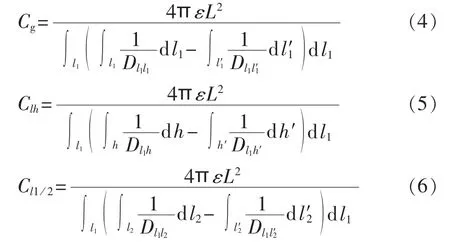
其中，L为桨叶长度；ε为空间电导率；D为两微元之间的距离。

导体的电感包括内电感与外电感两部分。但考虑到雷电流变化迅速，并且雷击暂态过程时间比较短暂，一般在防雷电气参数计算中，通常认定内电感可以忽略不计，仅考虑外电感即可［20］。对于空间导体而言，（外）电感为自感和互感之和。目前国内外学者普遍运用电磁场理论中的Neumann积分法计算自感和互感［21］。根据桨叶几何关系可以求得桨叶自电感 Lg、桨叶与塔筒的互感 Llh和桨叶间互感 Ll1／2，分别如式（7）—（9）所示。

其中，θ1、θ2、θ3分别为桨叶与桨叶镜像、桨叶与塔筒、桨叶与桨叶之间的夹角；μ为空间磁导率。

由上述分析可以得到单个叶片的总电容、总电感，根据波阻抗的定义式可以求得叶片波阻抗如式（10）所示。

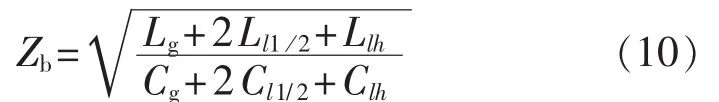
该桨叶波阻抗模型与传统风机桨叶波阻抗模型相比不仅考虑了桨叶的长度、塔筒的高度，还考虑了桨叶旋转角度的影响。

1.3 海上风机塔筒波阻抗模型

当雷电流通过风机塔筒时，将风机的塔体视为一个垂直圆柱体，忽略上下底面半径的差别。雷电流经过风机塔体的过程可视为以球面波的形式传播［22］，与锥形天线的波过程相似，可采用圆锥天线理论［23-25］求其波阻抗。

图4为海上风机塔体部分的圆锥天线等效模型。图中，H为塔体高度；r为上下底半径。选取风机塔体上某一微分元段dh，距离地面高度为hd，所形成的倒圆锥顶点O为圆柱中心在地面上的投影点，θd为圆锥顶角的一半。选取任意微元角dθ，并将点O与微分元段外边界的距离标记为R，则微圆弧的弧长即为Rdθ，并且根据图中几何关系可知：r=Rsinθd，

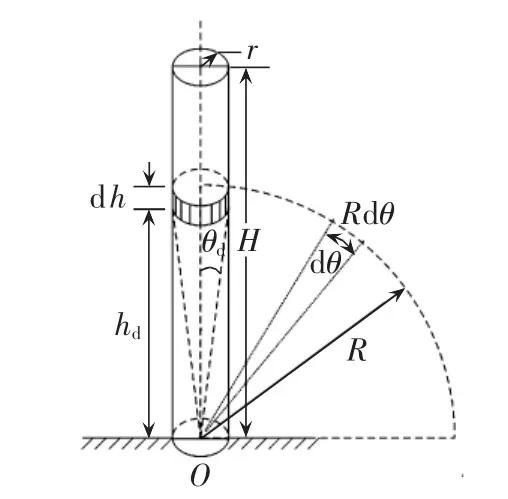
图4 海上风机塔体锥形天线模型Fig.4 Conical antenna model of offshore wind turbine tower

由圆锥天线理论可求得微分元段dh的波阻抗 Z′为：

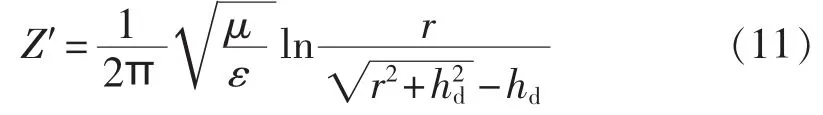
沿着塔体求取积分并平均后，即可推导得出整个海上风机塔体等效波阻抗Z为：

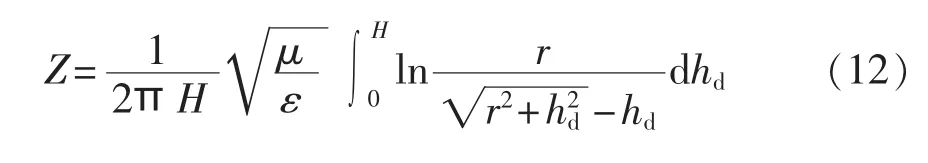
2 海上风机一体化电磁暂态模型

2.1 雷电参数模型

雷电是一种随机发生的大气中云与云或云与地面之间的放电现象，自然界的雷电有正负极性之分，为了表述方便，研究中将其设定为正极性。由于雷电流双指数模型可方便地进行微分、积分，故采用双指数模型模拟雷电流。其数学表达式如式（13）所示。

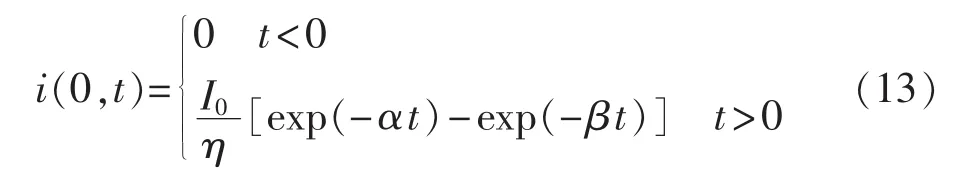
其中，I0为雷电流峰值；η为雷电流的峰值修正系数；α和β分别为由波头时间和波尾时间决定的时间常数。基于雷电观测以及前人的研究［9，26］，本文采用8／20 μs标准雷电流波形模拟风机所遭受的雷电流，雷电流峰值取120kA，参数α和β分别取7.713×104s和2.484×105s。根据文献［21］对雷电流通道进行简化，忽略先导的影响和雷电流波形在放电通道内的畸变，假设电通道垂直于地面且电流集中在通道的轴线上，利用彼得逊电流源等效电路代替雷电流放电过程，其中雷电流通道波阻抗取为300 Ω。

2.2 海上风机一体化电磁暂态模型

根据上文建立的风机桨叶、塔体波阻抗数学模型和海上风机冲击接地电阻模型，按照雷电流在海上风机的实际泄流顺序进行连接，可得到海上风机雷击暂态一体化模型，如图5所示。图中，Zb1、Zb2、Zb3为风机的3片桨叶波阻抗；Zt为风机塔体部分的波阻抗；Rg为海上风机等效冲击接地电阻。

图5 海上风机雷击暂态一体化模型Fig.5 Transient integration model of offshore wind turbine with lightning stroke

利用本文波阻抗计算方法和传统风机波阻抗计算方法［15］分别建立风机一体化模型和传统模型，并在ATP-EMTP软件中进行仿真，取塔筒顶端机舱处的暂态过电压为研究对象，结果如图6所示。

从仿真结果可以看出两者在幅值和振荡频率上已有较为明显的差别。新建的风机一体化模型综合考虑了桨叶旋转角度、塔筒高度、桨叶长度等因素的影响，更加贴合实际的风机运行状态；传统的风机波阻抗模型在一定程度上夸大了雷击过电压的幅值，可能导致采用更高等级的防雷措施而增加不必要的成本。

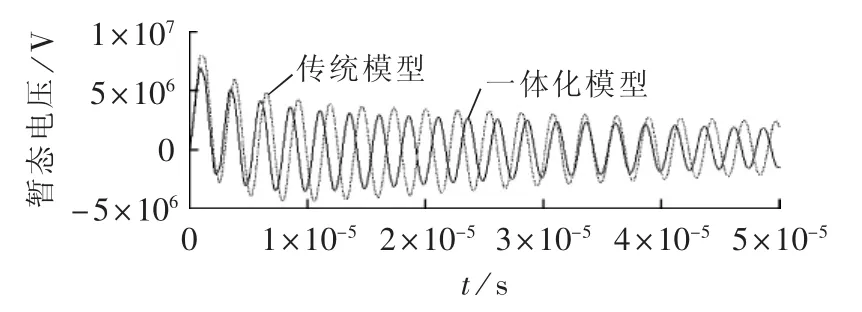
图6 一体化模型与传统模型暂态电压对比图Fig.6 Transient voltage comparison between integration model and traditional model

3 海上风机雷电冲击暂态特性影响因素

以单桩式海上风机作为仿真中的标准机型，机型参数如下：塔体高度H=120 m，塔体平均半径rt=2.3 m，塔壁平均厚度0.0257 m，桨叶长度L=70 m，桨叶位置为图7所示位置I，引下线半径rb=0.001m，海水层深度h1=15m，海水电阻率ρ1=5Ω·m，砂石土壤电阻率ρ2=1500 Ω·m，接地基础半径rg=3 m，伸入海床部分长度h2=10 m，接地体总长lg=25 m。利用上述参数对海上风机机舱处暂态电位进行分析。内部设备线路采用分离式接地系统，则内部设备暂态电位升远小于机舱暂态电位，设备与机舱电位差可近似等于机舱电位［5］，故下述以机舱处暂态电位分析为主。

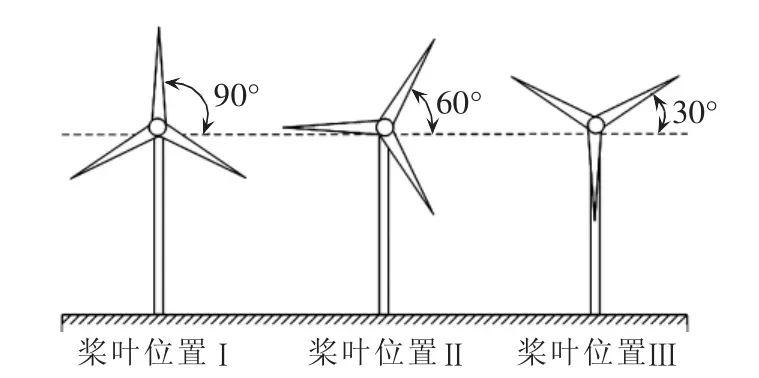
图7 风机桨叶的3种典型空间位置Fig.7 Three typical blade positions

3.1 海水层深度对风机雷电冲击暂态响应的影响

对于海上风机而言，海水层深度是影响海上风机接地参数的一个重要因素。由式（3）可知，随着海水层降低，海上风机冲击接地电阻会增大，当海水层深度为0时，可以近似看作陆上风机，根据土壤层电阻率不同，其冲击接地电阻在［0，20） Ω［27］范围内变化。在不同海洋深度下，由一体化模型得到风机机舱处的暂态电位如图8所示。

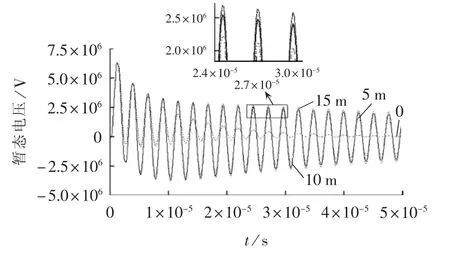
图8 海水层深度对暂态电压的影响Fig.8 Effect of ocean depth on transient voltage

从仿真结果可以看出，机舱处暂态电位升的最大值与海水层深度无关，且最大值出现在第一个振荡周期内；随着时间的推移，海水层越浅振荡幅值衰减越快，当海水层深度为0时，振荡衰减最快。

由于风机整体阻抗呈现感性，故在机舱处的电压值可用式（14）表示。

其中，Leq为风机等效电感；Req为风机等效电阻；i为雷电流；di／dt为雷电流本身的变化和电流反射波变化两部分之和，当两者变化同相时出现极大值，反相时出现极小值，故等号右边第1项为振荡项，所以机舱处电压波形会出现明显的振荡现象。

在雷电流波前时间内雷电流陡度很大，当反射波与注入雷电流波同相时，di／dt的数值达到整个过程最大值，式（14）数值主要由等号右边第1项决定，所以机舱处暂态电位最大值几乎不受海水层深度的影响，而双指数电流波在波前时间内越靠前其陡度越大，所以过电压最大值一般出现在第一个振荡周期内；当反射波与注入雷电流波反相时，di／dt的绝对值减小，式（14）等号右边第2项的作用体现出来，从而出现了图8中暂态电压在前几个振荡周期波谷处不重合、波峰处重合的现象，这种现象在接地电阻较大时（图8中0曲线）最为明显。

在雷电流波尾时间内，雷电流陡度减缓，此时振荡剧烈程度较波前时间内有所降低。由于塔筒波阻抗数值大于接地电阻，而海水层越浅，冲击接地电阻越大，故电流波反射系数越小，振荡幅值越小。另外由于电阻消耗能量，接地电阻越大则振荡衰减越快。

对比图8中0曲线可以看出，海上风机比陆上风机的振荡更加剧烈，在保证海上风机接地体电位升允许的情况下，对接地装置进行处理，适当增加接地电阻的阻值可有效地加快机舱处暂态电位的衰减速度。图9为标准机型与接地装置优化到2 Ω时塔筒顶部电压的对比图。

3.2 桨叶长度和塔筒高度对风机雷电冲击暂态响应的影响

保持其他参数不变，取不同桨叶长度（L=40 m、L=70 m与L=100 m）以及塔筒高度（H=90 m、H=120 m与H=150 m）进行仿真，分析桨叶长度和塔筒高度对机舱处暂态电位跃升（见图10）和振荡频率（见表1）的影响。

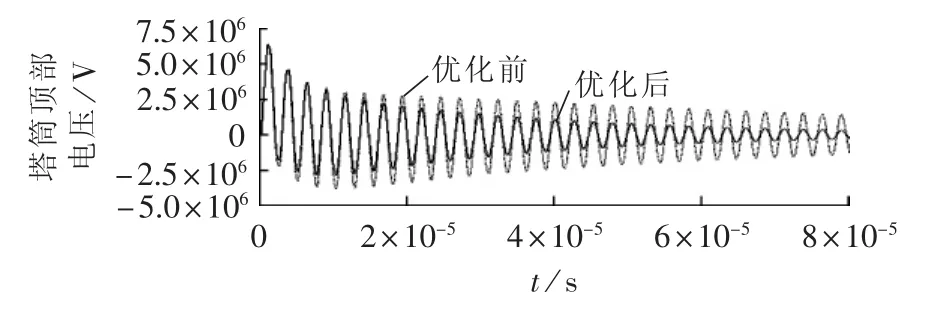
图9 接地电阻优化前后暂态电压对比图Fig.9 Comparison of transient voltage before and after optimization of ground resistance

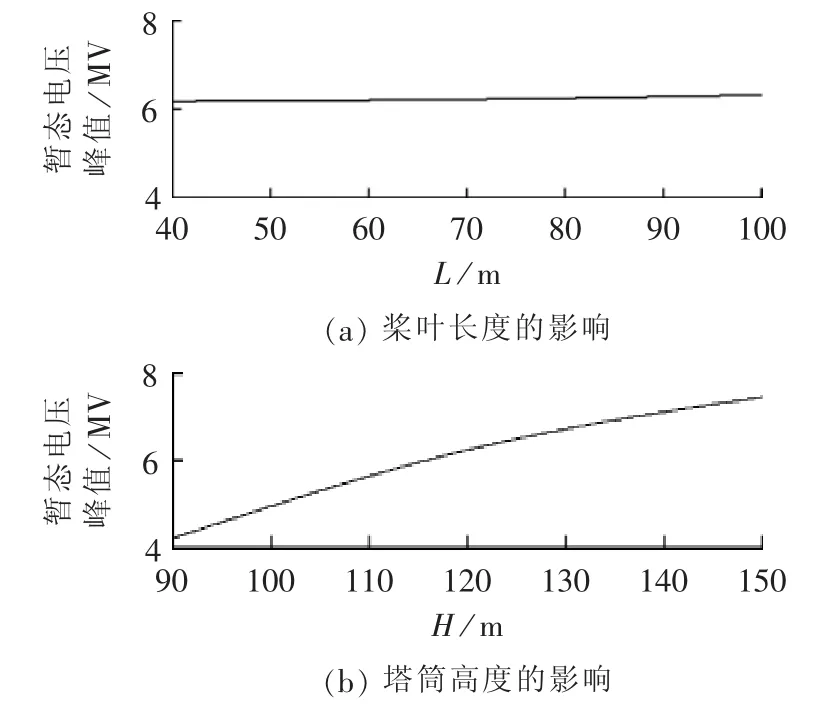
图10 桨叶长度和塔筒高度对暂态电压峰值的影响Fig.10 Effect of blade length and tower height on transient voltage peak

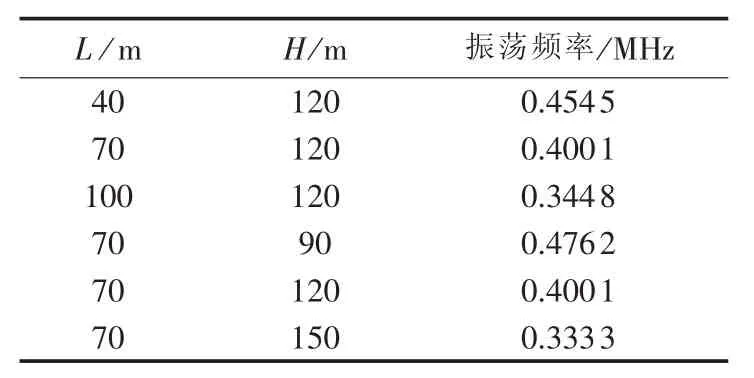
表1 桨叶长度和塔筒高度对暂态电压振荡频率的影响Table 1 Effect of blade length and tower height on transient voltage oscillation frequency

由图10可以看出，随着桨叶长度和塔筒高度的增加，风机机舱处的暂态电位都呈现上升趋势，但桨叶长度增加对塔筒顶端电位的影响较小。这是由于机舱处暂态电压峰值可近似用式（15）表示。

其中，Up为机舱处电压峰值；Uh和Ug分别为此刻塔筒和接地体上的电压降，Uh与塔筒高度H正相关，Ug几乎不变。当风机塔筒高度增加时，Uh随之增大，Up明显上升。风机桨叶长度的增加对Uh和Ug的影响较小，所以Up变化不明显。

由表1可看出，振荡频率与风机桨叶长度和塔筒高度负相关。桨叶长度和塔筒高度的增加相当于雷电流传播路径的增长，则机舱处暂态电位振荡的频率就减小，其频率数值约等于 v／［4（H+L）］，其中v为雷电流波在风机上的传播速度。

3.3 雷电参数对风机雷电冲击暂态响应的影响

波前时间与波尾时间是决定雷电流波形的2个主要参数，图 11 为 4 ／20 μs、8 ／20 μs、8 ／50 μs 3 个不同雷电参数下的雷电流波。

图11 不同雷电参数下的雷电流波Fig.11 Lightning current waveforms with different lightning parameters

利用上述3种不同波前、波尾时间的雷电流波形进行仿真得到风机机舱处暂态电位如表2所示。可看出雷电流参数中波前时间对雷击海上风机暂态过程的影响较大。其原因仍可用式（14）进行分析：由于雷电流的波前时间远远小于波尾时间，当波前时间减小时，高频分量增加明显，di／dt数值变大，则暂态电位峰值升高越明显；而雷电流波尾比较平缓，波尾时间的改变对di／dt数值影响较小，则对机舱处暂态电位的影响也较小。

表2 不同雷电参数下雷击暂态响应情况Table 2 Transient response caused by lightning stroke with different lightning parameters

3.4 雷击点对风机雷电冲击暂态响应的影响

海上风机遭受雷击后，雷电流可能会从风机桨叶尖端接闪器或机舱尾部避雷针注入，因此不同的雷击点位置将改变雷电流在风机上的泄流路径，进而对雷击暂态过程产生影响。下面分别对雷电击中风机桨叶尖端接闪器和机舱尾部避雷针这2种不同雷击点的情况进行分析（见图12），研究风机机舱处暂态电位响应情况。

图12 雷击点对暂态电压峰值的影响Fig.12 Effect of lightning strike point on transient voltage peak

由图12可以看出，雷电流流通路径的改变，导致雷击桨叶尖端接闪器时机舱处暂态电位峰值比雷击机舱尾部避雷针时大约高出7.6%，这将增加机舱内部电力系统和控制系统的雷击损坏故障率。所以在机舱内部设备的防雷设计中，应以雷击桨叶情况为研究对象。

3.5 桨叶旋转位置对风机雷电冲击暂态响应的影响

保持其他参数不变，选取3种典型的桨叶空间位置Ⅰ、Ⅱ、Ⅲ，如图7所示。

根据所建立的风机波阻抗模型得到风机在不同叶片旋转角度下的暂态响应，如表3所示。由表3可看出，随着桨叶转动，风机机舱处暂态电压峰值发生了变化。由1.1节可知，这主要是因为桨叶旋转改变了风机各部分电感、电容参数，从而改变了波阻抗，使得桨叶和塔筒交界处电流折反射系数发生改变。由对比结果可知，当桨叶处于位置Ⅰ时，机舱处雷电暂态电位跃升为最高水平，此种情况下的雷击对机舱内部设备产生的危害最严重。

表3 桨叶位置对暂态电压峰值的影响Table 3 Effect of blade position on transient voltage peak

结合3.4、3.5节，当研究风机机舱内部绝缘水平时，要在雷击位置Ⅰ桨叶尖端的情况下进行分析，此时不仅风机的引雷能力最强，而且机舱处的暂态电压达到最大值。

4 结论

a.根据海上风机环境的特点以及桨叶旋转特性，建立了海上风机的一体化多波阻抗模型；

b.海上风机遭受雷击时机舱处暂态过电压振荡幅值随海水深度减小而减小，对于海上风机而言，适当增加接地电阻阻值可有效减缓机舱处暂态电压的振荡；

c.机舱处雷电暂态过电压频率主要受桨叶长度和塔筒高度的影响，其中塔筒高度的增加还会显著提高机舱暂态电压的幅值；

d.雷电流波前时间、雷击点、桨叶旋转位置都会对机舱暂态电压峰值产生影响，在雷电防护设计时要对上述参数加以说明。

参考文献：

［1］张国伟，龚光彩，吴治．风能利用的现状及展望［J］．节能技术，2007，25（1）：71-76．ZHANG Guowei，GONG Guangcai，WU Zhi.State of the art and prospects on wind energy［J］.Energy Conservation Technology，2007，25（1）：71-76.

［2］李国庆，刘玢，陈厚合．大规模风电并网系统容量效益裕度计算模型研究［J］．电力自动化设备，2016，36（7）：1-6．LI Guoqing，LIU Bin，CHEN Houhe.CBM calculation model for power system with large-scale wind power［J］.Electric Power Automation Equipment，2016，36（7）：1-6.

［3］丰颖，贠志皓，周琼，等．考虑风电接入的在线风险评估和预防控制［J］．电力自动化设备，2017，37（2）：61-68．FENG Ying，YUN Zhihao，ZHOU Qiong，et al.Online risk assessment and preventive control considering wind-power integration［J］.Electric Power Automation Equipment，2017，37（2）：61-68.

［4］蒋程，刘文霞，张建华，等．含风电接入的发输电系统风险评估［J］．电工技术学报，2014，29（2）：260-270．JIANG Cheng，LIU Wenxia，ZHANG Jianhua，et al.Risk assessment of generation and transmission systems considering wind power penetration［J］.Transactions of China Electrotechnical Society，2014，29（2）：260-270.

［5］肖翔，张小青，李聪，等．风电机组雷电过电压的仿真分析［J］．电工技术学报，2015，30（24）：237-244．XIAO Xiang，ZHANG Xiaoqing，LI Cong，et al.Simulation analysis on overvoltage in wind turbines by lightning stroke［J］.Transactions of China Electrotechnical Society，2015，30（24）：237-244.

［6］YAMAMOTO K，NODAT，YOKOYAMA S，et al.An experimental study of lightning overvoltages in wind turbine generation systems using a reduced-size model［J］.Electrical Engineering in Japan，2007，158（4）：22-30.

［7］方超颖，李炬添，张曾，等．接地电阻对风机桨叶引雷能力影响模拟试验［J］．电网技术，2015，39（6）：1709-1713．FANG Chaoying，LIJutian，ZHANG Zeng，etal.Experimental study of the influence of the grounding resistance on triggered lightning abilities of wind turbine’s flabellum［J］.Power System Technology，2015，39（6）：1709-1713.

［8］张波，薛惠中，金祖山，等．遭受雷击时输电杆塔及其接地装置的暂态电位分布［J］．高电压技术，2013，39（2）：393-398．ZHANG Bo，XUE Huizhong，JIN Zushan，et al.Transient potential distribution of transmission tower and its grounding device under lightning［J］.High Voltage Engineering，2013，39（2）：393-398.

［9］张波，薛惠中，张宝全，等．雷击风机时叶片和塔筒对接地装置冲击接地特性的影响［J］．高电压技术，2012，38（10）：2675-2682．ZHANG Bo，XUE Huizhong，ZHANG Baoquan，et al.Influence of the wind vane tower barrel on the earthing connection’s impulse earthing characteristics in a lightning shock［J］.High Voltage Engineering，2012，38（10）：2675-2682.

［10］YOH Y，TOSHIAKI U.FDTD transient analysis of ring earth electrode［C］∥Proceedings of the 41st International Universities Power Engineering Conference.Newcastle Upon Tyne，UK：IEEE，2006：133-136.

［11］YOH Y，TOSHIAKIF，TOSHIAKIU.How doesringearth electrode effect to wind turbine？［C］∥42nd International UniversitiesPowerEngineering Conference.Brighton，UK：IEEE，2007：796-799.

［12］LORENTZOU M I，HATZIARGYRIOU N D，PAPADIAS B C.Analysis of wind turbine grounding systems［C］∥10th Mediterranean Electrotechnical Conference. Lemesos，Cyprus：IEEE，2000：936-939.

［13］赵海翔，王晓蓉．风电机组的雷击过电压分析［J］．电网技术，2004，28（4）：27-29．ZHAO Haixiang，WANG Xiaorong.Overvoltage analysis of wind turbines due to lightning stroke［J］.Power System Technology，2004，28（4）：27-29.

［14］MALCOLM N，AGGARWAL R K.Transient overvoltage study of an island wind farm［C］∥2012 47th International Universities Power Engineering Conference.London，UK：IEEE，2012：1-6.

［15］JIANG A，FU Z，HE Y，et al.Surge analysis of onshore wind farm due to multiple lightning strokes［C］∥International Conference on Lightning Protection.Shanghai，China：IEEE，2014：1122-1127.

［16］吴志良，王凤武．海上风电场风机基础型式及计算方法［J］．水运工程，2008（10）：249-258．WU Zhiliang，WANG Fengwu.Blower foundation type in marine wind electric field and calculation method［J］.Port&Waterway Engineering，2008（10）：249-258.

［17］MA J，DAWALIBI P，SOUTHEY R D.On the equivalence of uniform and two-layer soils to multilayer soils in the analysis of grounding systems［J］.IEE Proceedings-Generation，Transmission and Distribution，1996，143（1）：49-55.

［18］潘文霞，刘铜锤，王兵，等．分层土壤任意块状基础的接地计算方法［J］．电工技术学报，2016，31（7）：145-151．PAN Wenxia，LIU Tongchui，WANG Bing，etal.Grounding computation method for layered-soil with arbitrary massive texture foundation［J］.Transactions of China Electrotechnical Society，2016，31（7）：145-151.

［19］张小青．垂直接地体的冲击电阻与冲击系数［J］．电力学报，2000（3）：155-157．ZHANG Xiaoqing.The impulse resistance and coefficient of vertical grounding rod［J］.Journal of Electric Power，2000（3）：155-157.

［20］刘成华，张小青，薛洁，等．防雷系统中含倾斜导体的电气参数的计算方法［J］．电瓷避雷器，2012（2）：81-85．LIU Chenghua，ZHANG Xiaoqing，XUE Jie，et al.A calculation method of the electrical parameters of sloping conductors in lightning protection systems［J］.Insulators and Surge Arresters，2012（2）：81-85.

［21］王晓辉．风力发电机组雷电暂态效应的研究［D］．北京：北京交通大学，2010．WANG Xiaohui.Investigations on the electromagnetic effects in wind turbines struck by lightning［D］.Beijing：Beijing Jiaotong University，2010.

［22］牧原，曾楚英．杆塔波阻抗的研究［J］．高电压技术，1992（2）：9-13．MU Yuan，ZENG Chuying.Study of tower surge impedance［J］.High Voltage Engineering，1992（2）：9-13.

［23］GUTIERREZ R J A，MORENO P，NAREDO J L，et al.Nonuniform transmission tower model for lightning transient studies［J］.IEEE Transactions on Power Delivery，2004，19（2）：490-496.

［24］JORDAN E C.Electromagnetic waves and radiating systems［J］.American Journal of Physics，1951，19（8）：477-478.

［25］杜林，糜翔，杨勇，等．雷击输电线路杆塔时的杆塔等效模型［J］．高电压技术，2011，37（1）：28-33．DU Lin，MI Xiang，YANG Yong，etal.Equivalentmodelof transmission tower under lightning striking［J］.High Voltage Engineering，2011，37（1）：28-33.

［26］王学良，张科杰，余田野，等．基于LLS的雷电流波头时间分布特征［J］．气象科技，2016，44（2）：313-318．WANG Xueliang，ZHANG Kejie，YU Tianye，etal.Temporal characteristics of lightning current wave-front time based on LLS［J］.Meteorological Science& Technology，2016，44（2）：313-318.

［27］张永记，司马文霞，张志劲．防雷分析中杆塔模型的研究现状［J］．高电压技术，2006，32（7）：93-97．ZHANG Yongji，SIMA Wenxia，ZHANG Zhijin.Summary of the study of tower models for lightning protection analysis［J］.High Voltage Engineering，2006，32（7）：93-97.