基于短路电流辨识双馈感应发电机的模型参数

潘学萍 ，殷紫吟 ，鞠 平 ，吴 峰 ，金宇清 ，马 倩

（1．河海大学 能源与电气学院，江苏 南京 211100；2.国网江苏省电力公司，江苏 南京 210024）

0 引言

建模是电力系统计算、分析以及运行控制的基础。合理而精准的风电机组模型参数是保证电力系统电磁暂态和机电暂态仿真分析正确性的前提，如何得到更接近实际风电机组的模型参数是电力系统学术界和工业界关注的热点。

目前关于风电机组参数辨识方面的研究已有较多报道。文献［1］基于系统频率扰动，采用有功功率受扰轨线辨识定速风电机组的惯量；文献［2］提出根据风速扰动辨识风电机组传动系统的参数；文献［3］提出在变流器控制环节的量测信号上施加扰动，辨识控制环节各参数；文献［4］指出由于双馈风电机组的机械动态与电气动态解耦，因此提出基于2种不同类型的扰动进行参数辨识，即基于风速扰动辨识传动系统参数，再基于风电机组出口的电压跌落扰动辨识双馈感应发电机（DFIG）的参数。然而由于变流器控制环节与DFIG的动态特性耦合较强，电压跌落下风电机组出口的有功功率、无功功率受扰轨线动态不仅与DFIG密切相关，受变流器控制环节的影响也较大。因此基于电压跌落试验辨识DFIG参数时，如果控制器参数给定值不准确，将导致较大的发电机参数辨识误差。

为了辨识DFIG的各参数，本文提出基于三相短路电流进行DFIG参数辨识的方法。该方法已成功应用于同步发电机的参数辨识，并出台了相关标准［5-7］。然而将该方法应用于DFIG的参数辨识目前还未见报道。

根据短路电流辨识DFIG参数的前提是获取短路电流的解析表达［8］。在双馈风电机组短路电流的解析研究方面，文献［9］假设故障期间DFIG的转子旋转速度、转子励磁电压和电网频率均保持不变，基于DFIG的磁链方程，推导了定转子短路电流的解析表达式。但是该文未考虑转子电压动态，未计及变流器控制环节的作用，短路电流解析式过于复杂。文献［10］假设故障期间转子励磁电压保持不变，推导了DFIG三相短路电流的解析模型。文献［11］研究了DFIG三相短路电流的实用计算方法，但未考虑变流器控制环节的作用。文献［12］讨论了风电机组端口三相短路情况下定转子电流的解析表达，定性分析了变流器控制环节对短路电流的影响，但未能给出影响的具体表达。文献［13-14］从双馈风电机组的控制策略对其故障特性的影响机制出发，对双馈风电机组在电网短路故障下的动态过程进行了分析，推导了适用于不同电压跌落程度下并网双馈风电机组的短路电流。文献［15-18］通过解析方法推导了撬棒（Crowbar）保护电路投入后，DFIG定子磁链、转子磁链的全响应，进而给出了电网电压对称和不对称跌落下DFIG短路电流的时域解析表达式。文献［19-20］分析了低电压穿越控制策略对短路电流的影响机理，建立了双馈风电机组短路电流的计算模型。

本文首先分析了双馈风电机组在机端发生三相短路故障时的电磁暂态特性，给出了短路电流的解析表达式，用以拟合双馈风电机组在相同扰动下的受扰轨迹，据此辨识DFIG的参数，最后还对辨识结果进行了误差分析。

1 双馈风电机组三相短路电流解析计算

与同步发电机不同的是，双馈风电机组的短路电流不仅受到Crowbar电路影响，在故障过程中控制器的动态特性也是其重要的影响因素之一。文献［19］指出：由于变流器控制环节的响应速度较快，其动态过程也较快。本文在基于双馈风电机组短路电流的解析表达式辨识DFIG模型参数时，所建立的模型中不安装Crowbar装置，且选择受扰轨线时间窗口为变流器控制环节的动态基本结束后的时段进行参数辨识。

本文采用文献［10］推导的短路电流进行参数辨识，短路电流推导结果假定故障前后励磁电压恒定。由于本文选择在变流器控制环节的动态基本结束后的时段进行参数辨识，因此文献［10］的假设对参数辨识的影响不大。

文献［10］将双馈风电机组的短路电流看作由零输入响应和零状态响应组成。零输入响应包括定转子侧磁链初值引起的电流，零状态响应包括转子侧电压产生的电流。最终得到的三相短路电流的解析表达式见式（1）、（2）。

其中，isd和isq分别为定子d轴电流和q轴电流；ωs为同步转速；s为滑差；Lm为定转子互感；Ls=Lsσ+Lm、Lr=Lrσ+Lm分别为定子自感、转子自感，Lsσ和 Lrσ分别为定子漏感、转子漏感；Rs、Rr分别为定子电阻、转子电阻；φs0和φr0分别为定子和转子磁链幅值的初值；δ1和 δ2分别为定子和转子磁链相位初值；is∞和δsu分别为定子侧稳态电流的幅值和相位；Ts和Tr分别为定子和转子衰减时间常数。

由式（1）、（2）可以看出，双馈风电机组出口发生三相短路故障后，短路电流中包含直流分量、频率为ωs的衰减交流分量以及频率为sωs的衰减交流分量。与同步发电机的短路电流相比，双馈风电机组的短路电流缺少了衰减的直流分量，但是增加了频率为sωs的衰减交流分量，这主要是因为同步发电机中通过直流进行励磁，而双馈风电机组通过转差频率进行励磁。

如果短路电流isd和isq已知，那么参数Lr／M、Lm／M、Ts以及Tr可以辨识，且由于ω0与初始状态有关，数值已知，则根据 Lr／M、Lm／M、Ts以及 Tr可以求得参数 Rs和Rr。根据Lr／M和Lm／M可求得LsLr以及Lm。因此如果短路电流isd和isq已知，那么参数Rs、Rr、LsLr以及 Lm可以辨识，但是参数 Ls和 Lr不可以单独辨识。

2 DFIG参数可辨识性及辨识难易度分析

进行参数辨识前，需知道参数的可辨识性及参数辨识的难易度。文献［21］提出，可采用轨迹灵敏度的方法衡量参数的可辨识性以及参数辨识的难易度。如果若干个参数的轨迹灵敏度同时过零点，则可以判定这些参数不是唯一可辨识的。如果所有参数的灵敏度都不同时过零点，则可以判定这些参数唯一可辨识；且轨迹灵敏度越大的参数，其对系统的动态行为影响越大，也越容易辨识。

以图1所示的双馈风电机组并联于无穷大系统为例，基于MATLAB／Simulink平台搭建该系统仿真模型，DFIG采用相量模型，各参数取值与原系统参数一致。稳态运行时，风电机组的风速为14 m／s，稳态输出功率为0.88 p.u.。

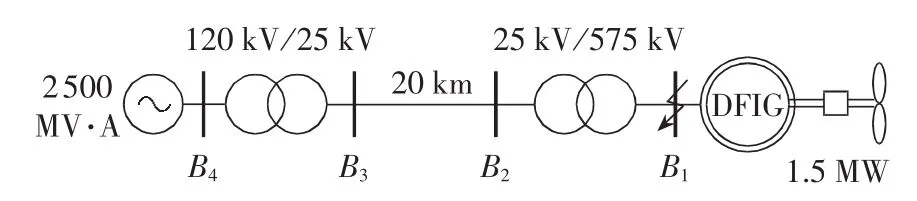
图1 DFIG风电场仿真模型Fig.1 Simulation model of DFIG-based wind farm

设置t=1 s时发电机端口母线B1处发生三相金属性短路故障，故障持续时间为0.2 s，即在1.2 s时故障消失。仿真得到风电机组出口的短路电流受扰轨线。使得DFIG参数（定子电阻Rs、转子电阻Rr、定子漏感 Lsσ、转子漏感 Lrσ以及定转子互感 Lm）变化10%，其余参数不变，计算各参数的轨迹灵敏度（标幺值），见图 2。

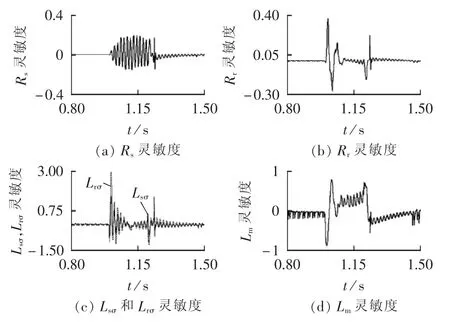
图2 DFIG各参数灵敏度曲线Fig.2 Sensitivity curves of DFIG parameters

从图2的灵敏度曲线形状可看出：参数Lsσ和Lrσ的灵敏度轨迹基本一致，这2个参数不能区分辨识，其他参数能够唯一辨识，这与前述的解析结果相同。为了定量比较各参数轨迹灵敏度的大小，进一步计算各参数的轨迹灵敏度大小，见式（6）。

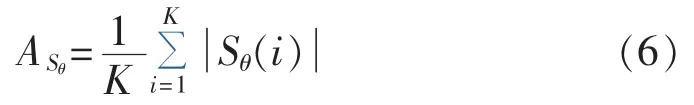
其中，ASθ为参数 θ的轨迹灵敏度；Sθ（i）为观察时窗内参数θ的第i个点的轨迹灵敏度数值；K为观察时窗内总点数，即时间长度除以时间步长。表1给出了不同观察时窗内各参数灵敏度（标幺值）结果。需要说明的是，表1中受扰轨线的时间窗口选择从1.06 s开始，这主要是为了避开变流器控制环节的动态对短路电流的影响。由文献［19］的仿真结果可看出：转子电流在故障后0.05 s左右动态过程结束。故本文选择在故障0.06 s之后时间窗内的短路电流进行参数灵敏度计算以及参数辨识。

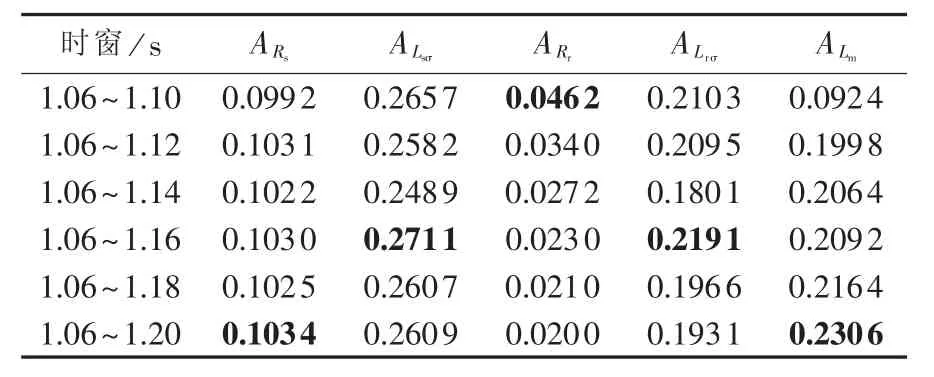
表1 不同时窗下轨迹灵敏度Table 1 Trajectory sensitivities under different time windows

由表1可以看出：定子电阻、定转子互感在故障持续期间1.06～1.20 s内灵敏度最高，转子电阻在故障后1.06～1.10 s内灵敏度最高，定子漏感转子漏感均在故障后1.06～1.16 s内灵敏度最高。在DFIG的5个参数中，漏感与互感的轨迹灵敏度较大，转子电阻的轨迹灵敏度最小。

3 基于三相短路电流的DFIG参数辨识

同样基于图1所示的仿真系统以及相同的运行状态，设置与第2节相同的故障获得风电机组短路电流受扰轨线。采用粒子群优化（PSO）算法进行参数辨识。参数辨识的目标函数为：

其中，isd_est和isq_est为基于辨识值的输出电流；N为受扰轨线时间窗口内的总点数。

根据表1的灵敏度结果，本节选择在时窗1.06～1.20 s内的短路电流受扰轨线辨识定子电阻Rs以及互感Lm、在时窗1.06～1.10 s内的短路电流受扰轨线辨识转子电阻Rr、在时窗1.06～1.16 s内的短路电流受扰轨线辨识定转子自感的乘积LsLr。

对DFIG参数分别进行了50次辨识。由于DFIG模型中定转子漏感难以区分辨识，因此这里以定转子自感之积LsLr作为待辨识参数。50次的参数辨识结果（标幺值）见图3。

根据50次的参数辨识结果，计算50次参数辨识结果的均值、方差以及均值偏差，见表2（表中真值、均值、方差均为标幺值）。

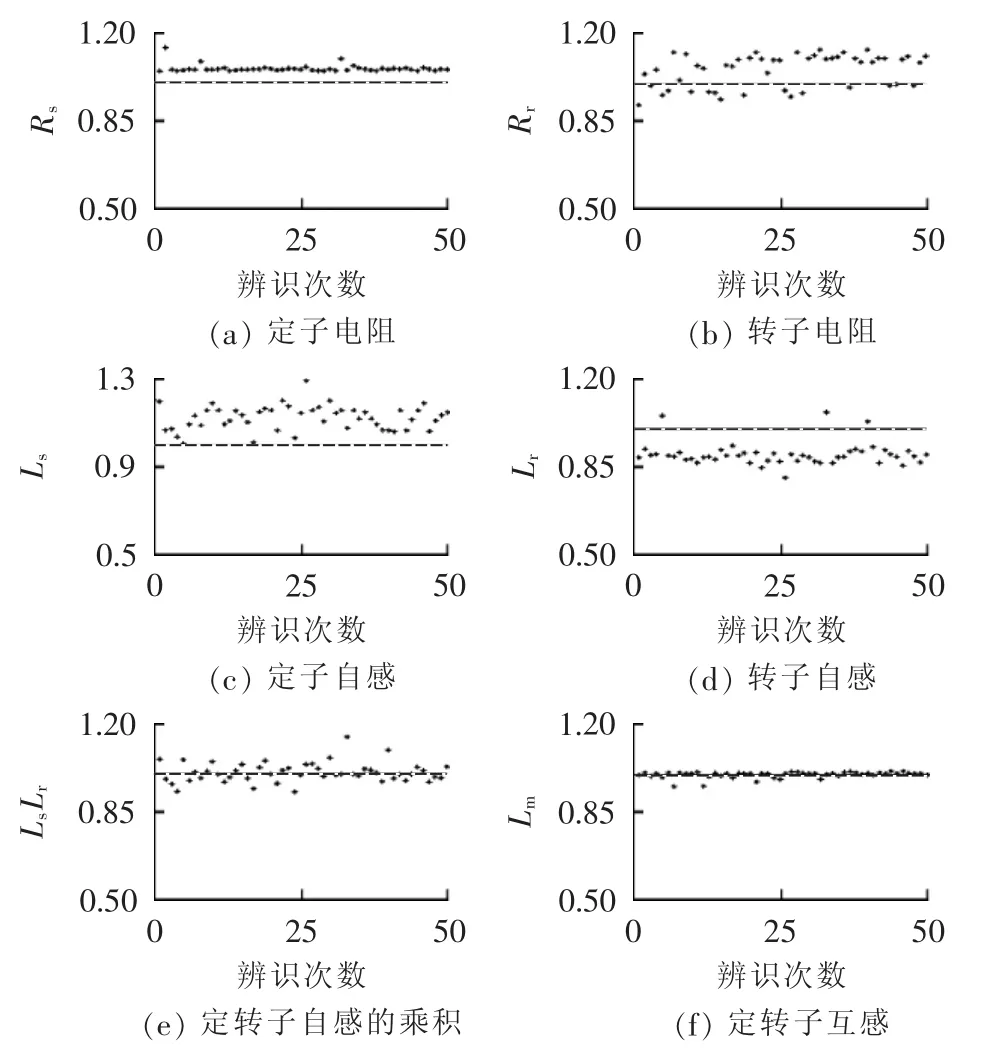
图3 DFIG各参数的辨识结果Fig.3 Identification results of DFIG parameters

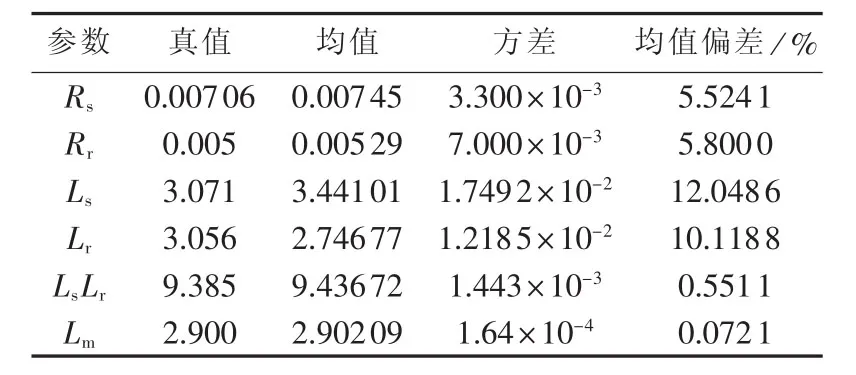
表2 DFIG参数辨识均值、方差和均值误差Table 2 Identification mean，variance and mean error of DFIG parameters

结合图3和表2可以看出：各参数的辨识值与仿真模型中的实际值相差不大，辨识效果较好。其中，互感Lm的50次辨识结果方差最小，辨识结果最稳定，辨识精度最高；定子自感Ls和转子自感Lr各自的辨识结果误差比较大，但是两者乘积LsLr的辨识结果误差比较小，反映了它们不能区分辨识；定子电阻的辨识值普遍高于实际值，这可能是由于简化的解析短路电流带来的偏差；转子电阻50次辨识值的方差相对比较大，辨识结果不稳定，辨识误差也比较大。

基于参数辨识结果与实际值的短路电流受扰轨线如图 4 所示（isd、isq为标幺值）。

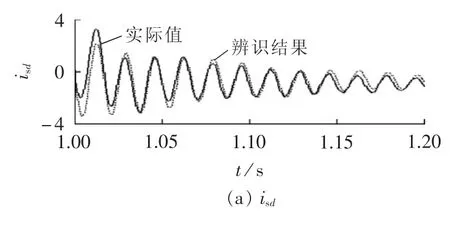
图4 实际短路电流和基于辨识结果的短路电流Fig.4 Real short circuit current and short circuit based on identification results

4 结论

本文提出基于双馈风电机组三相短路电流的风电机组模型参数辨识方法。由于双馈风电机组的短路电流受Crowbar动作、控制器环节的影响，因此本文在进行参数辨识时，所建立的模型中不安装Crowbar装置，且参数辨识时窗选择为变流器控制环节动作基本结束后的时段进行。

定子漏感Lsσ和转子漏感Lrσ的轨迹灵敏度曲线形状基本一致，这2个参数不能区分辨识，根据解析结果可知，定子自感与转子自感的乘积LsLr可辨识，因此本文将LsLr作为待辨识参数。

从参数辨识的结果可看出，互感Lm的辨识精度最高，转子电阻的轨迹灵敏度最小，辨识误差最大；其余参数的辨识精度较高。该结果与轨迹灵敏度分析结果一致。

本文在辨识DFIG参数的过程中未考虑变流器控制环节的影响。后续工作将进一步考虑变流器控制环节作用下的DFIG参数辨识方法。

参考文献：

［1］LITTLER T，FOX B，FLYNN D.Measurement-based estimation of wind farm inertia［C］∥Proceedings of IEEE Conference on Power Tech.St.Petersburg，Russia：IEEE，2005：1-5.

［2］潘学萍，高远，金宇清，等.风电机组驱动系统参数辨识［J］.电网技术，2013，37（7）：1990-1994.PAN Xueping，GAO Yuan，JIN Yuqing，et al.Parameter identification of drive system for fixed-speed wind power generation units［J］.Power System Technology，2013，37（7）：1990-1994.

［3］金宇清，鞠平，刘伟航，等.基于量测信号扰动的DFIG变流器控制参数辨识方法［J］. 电力系统自动化，2016，40（8）：36-42.JIN Yuqing，JU Ping，LIU Weihang，et al.Parmeter identification method for converter controller of DFIG based on measurement signal disturbance［J］.Automation of Electric Power Systems，2016，40（8）：36-42.

［4］潘学萍，鞠平，徐倩，等.双馈风力发电机参数分步辨识及观测量的选择［J］. 中国电机工程学报，2013，33（13）：116-126.PAN Xueping，JU Ping，XU Qian，et al.A two-step method for estimating DFIG parameters in a wind turbine and the measurement selection［J］.Proceedings of the CSEE，2013，33（13）：116-126.

［5］全国旋转电机标准化技术委员会.三相同步电机试验方法：GB／T 1029—1993［S］. 北京：中国标准出版社，1993.

［6］IEEE Power and Energy Society.IEEE guide for synchronous generatormodeling practices in stability analyses：IEEE Std 1110-1991［S］. ［S.l.］：IEEE，1991.

［7］IEEE Power and Energy Society.IEEE guide for synchronous generator modeling practices and applications in power system stability analysis：IEEE Std 1110-2002［S］. ［S.l.］：IEEE，2003.

［8］LOPEZ J，SANCHIS P，ROBOA X，et al.Dynamic behavior of the doubly fed induction generator during three-phase voltage dips［J］.IEEE Transactions on Energy Conversion，2007，22（3）：709-717.

［9］VICATOS M S，TEGOPOULOS J A.Transient state analysis of a doubly-fed induction generator under three phase short circuit［J］．IEEE Transactions on Energy Conversion，1991，6（1）：62-68．

［10］石一辉，鲁宗相，闵勇，等．双馈感应发电机三相短路电流解析计算模型［J］．电力系统自动化，2011，35（8）：38-43．SHI Yihui，LU Zongxiang，MIN Yong，et al.Practical calculation modelofthree-phase short-circuitfordoubly-fed induction generator［J］.Automation of Electric Power Systems，2011，35（8）：38-43．

［11］邢鲁华，陈青，吴长静，等．含双馈风电机组的电力系统短路电流实用计算方法［J］．电网技术，2013，37（4）：1121-1127．XING Luhua，CHEN Qing，WU Changjing，etal.A practical method to calculate short-circuitcurrentin powersystem connected with doubly fed induction generators［J］.Power System Technology，2013，37（4）：1121-1127．

［12］MORREN J，DE HAAN S W H.Short-circuit current of wind turbines with doubly fed induction generator［J］.IEEE Transactions on Energy Conversion，2007，2（1）：174-180.

［13］欧阳金鑫，熊小伏，张涵轶.电网短路时并网双馈风电机组的特性研究［J］. 中国电机工程学报，2011，31（22）：17-25．OUYANG Jinxin，XIONG Xiaofu，ZHANG Hanyi.Characteristics of DFIG-based wind generation under grid short circuit［J］.Proceedings of the CSEE，2011，31（22）：17-25．

［14］OUYANG Jinxin，XIONG Xiaofu.Research on short-circuit current of doubly fed induction generator under non-deep voltage drop［J］.Electric Power Systems Research，2014，107（2）：158-166.

［15］PANNELL G，ATKINSON D J，ZAHAWI B.Analytical study of grid-faultresponse ofwind turbine doubly fed induction generator［J］.IEEE Transactions on Energy Conversion，2010，25（4）：1081-1091.

［16］SULLA F，SVENSSON J，SAMUELSSON O.Symmetricaland unsymmetrical short-circuit current of squirrel-cage and doubly fed induction generators［J］.Electric Power System Research，2011，81（7）：1610-1618.

［17］郑涛，魏占朋，李娟，等．计及撬棒保护的双馈风电机组不对称短路电流特性分析［J］．电力系统保护与控制，2014，42（2）：7-12．ZHENG Tao，WEI Zhanpeng，LI Juan，et al.Unsymmetrical short circuit current analysis of doubly fed induction generators with Crowbar protection［J］.Power System Protection and Control，2014，42（2）：7-12．

［18］郑重，杨耕，耿华．电网故障下基于撬棒保护的双馈风电机组短路电流分析［J］．电力自动化设备，2012，32（11）：7-15.ZHENG Zhong，YANG Geng，GENG Hua.Short circuit current analysis for DFIG-based wind generation system with crowbar protection under grid faults［J］.Electric Power Automation Equipment，2012，32（11）：7-15.

［19］尹俊，毕天姝，薛安成，等.计及低电压穿越控制的双馈风力发电机组短路电流特性与故障分析方法研究［J］.电工技术学报，2015，30（23）：116-125.YIN Jun，BI Tianshu，XUE Ancheng，et al.Study on short circuit currentand faultanalysismethod ofdouble fed induction generatorwith low voltage ride-through controlstrategy ［J］.Transactions of China Electrotechnical Society，2015，30 （23）：116-125.

［20］孔祥平，张哲，尹项根，等．计及励磁调节特性影响的双馈风力发电机组故障电流特性［J］．电工技术学报，2014，29（4）：256-265．KONG Xiangping，ZHANG Zhe，YIN Xianggen，etal.Fault currentcharacteristics ofDFIG considering excitation and regulation characteristics［J］.Transactions of China Electrotechnical Society，2014，29（4）：256-265．

［21］谢会玲，鞠平，罗建裕，等．基于灵敏度计算的电力系统参数可辨识性分析［J］．电力系统自动化，2009，33（7）：17-21．XIE Huiling，JU Ping，LUO Jianyu，et al.Identifiability analysis of load parameters based on sensitivity calculation［J］.Automation of Electric Power Systems，2009，33（7）：17-21．