基于故障电流解析表达的FCL协助DFIG低电压穿越研究

李生虎，黄杰杰，吴正阳

（合肥工业大学 电气与自动化工程学院，安徽 合肥 230009）

0 引言

风电机组需要具有低电压穿越（LVRT）能力［1-2］，在不违背其安全约束的前提下，为电网提供部分无功和有功支撑。双馈感应电机（DFIG）的定子与电网直接相连，易受电网电压跌落影响。在DFIG机端与公共耦合点（PCC）间投入故障电流限制器（FCL），可提升机端电压，帮助实现故障穿越。

通常PCC与定子间阻抗较小，故障后两者电压近似相等，即定子电压跌落幅度确定，因此可忽略网侧变流器（GSC）电流对定子电压的影响，仅基于感应电机方程求解故障电流［3-5］。在DFIG机端串联FCL，增加了定子与PCC间阻抗，GSC电流对定子电压影响较大。文献［6］在DFIG机端串联FCL，假设定子电压已知，不能反映FCL阻抗和GSC电流的影响。对串联FCL进行故障电流分析，需将DFIG与 FCL进行整体建模，从而综合反映转子侧变流器（RSC）、GSC控制与FCL阻抗对故障电流的影响。

考虑RSC与GSC控制，文献［7］指出功率外环控制在电压骤降的情况下会导致电流参考值剧烈增长，故本文在LVRT过程中取消RSC与GSC功率外环控制而改用恒定电流控制。文献［8］将RSC与GSC视为恒定电流源求解故障电流，与其功率外环控制相矛盾，且DFIG采用稳态模型。文献［9］在RSC电流内环中计及定子磁链暂态，实现了定转子电流解耦。RSC与GSC电流可作为定子电流求解的条件，但现有文献对恒定电流控制的电流表达式的研究严重不足。

采用FCL实现LVRT中比较关心的问题有FCL阻抗值与DFIG控制参数的选取。基于DFIG与FCL整体建模求解得到的故障电流解析表达可定量表达这两者对故障电流的影响，可用于参数选择。

如果采用定子电压定向，投入FCL初期定子电压相角随着电流振荡变化幅度较大，使得DFIG dq轴与xy轴夹角不断变化。在电网xy轴下统一分析 DFIG与FCL方程，此时RSC与GSC dq轴恒定电流在xy轴下为变化电流，不利于定子电流尽快稳定。

本文针对DFIG串联FCL实现LVRT中存在的问题，取消RSC与GSC功率外环，内环采用恒定电流控制，在RSC控制环节中计及定子磁链暂态，提出了RSC、GSC和DFIG故障电流的解析表达。该过程中将DFIG dq轴与电网xy轴重合，从而在dq轴与xy轴下皆实现恒电流控制。在不违背安全约束的前提下，比较故障过程中DFIG电磁转矩振荡，以选择RSC与GSC电流参考值、FCL阻抗及切出时间等控制参数。比较解析模型与动态仿真结果，验证了所提控制策略的效果。

1 DFIG机端串联FCL的故障电流解析表达

DFIG机端串联桥型FCL如图1所示［10］，其中用桨距角调节实现超速保护，用卸荷电路限制直流电压，用FCL提升机端电压，后两者目的不同。图中U、I、Z 分别代表电压、电流与阻抗，下标 s、r、g、T 分别代表定子、转子、GSC与出线变压器。正常工作时IGBT导通，FCL的限流电感LFCL和电阻RFCL被旁路；故障时IGBT关断，从而投入限流阻抗。

按电动机惯例，同步旋转坐标系下DFIG磁链为：

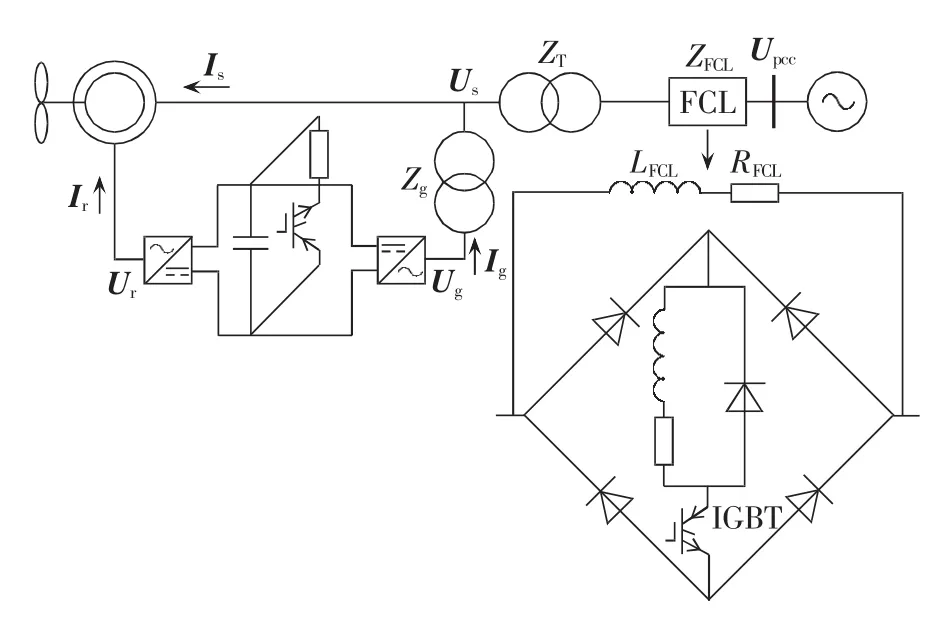
图1 使用FCL的DFIG LVRTFig.1 LVRT of DFIG with FCL

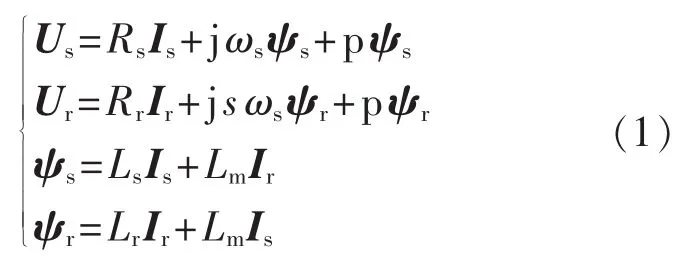
其中，ψ、L、R 分别为磁链、电感、电阻；ωs为同步转速；s为转差率；p为微分计算符。

引入PCC电压式（2），可得定子磁链的一阶微分方程式（3）：

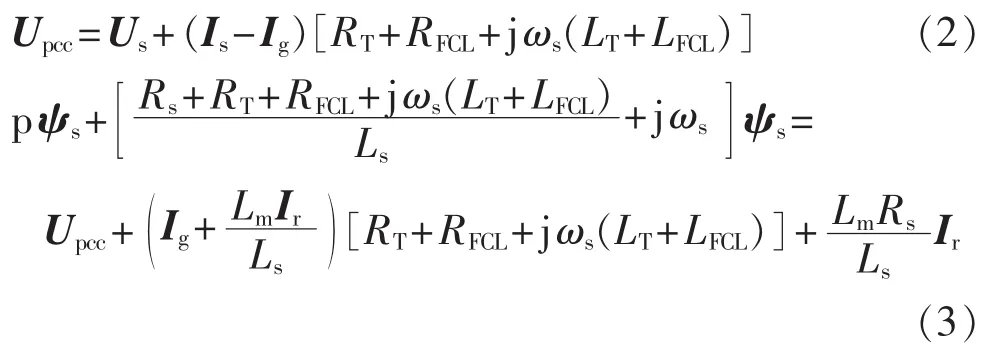
RSC与GSC电流会影响定子磁链。功率外环控制在电压骤降的情况下会导致电流参考值剧烈增长，故在LVRT过程中取消RSC与GSC功率外环，改为恒定电流控制，基于此推导RSC、GSC与定子电流。

1.1 RSC恒定电流控制

以恒定电流参考值Irefr代替RSC功率外环控制，基于 RSC 电压方程式（4）（其中 L′r=Lr-L2m／Ls）与RSC控制方程式（5）求解转子电流。

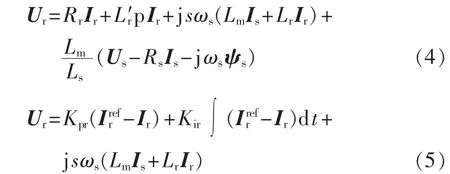
其中，Kpr、Kir分别为RSC电流控制的比例环节与积分环节系数；上标ref代表参考值。

联立方程求解时，定子磁链暂态（式（4）第二行）无法消去，电压跌落后定子磁链会振荡收敛至新的稳定值，其暂态不可忽略。在电流内环控制中引入定子磁链暂态，得到转子电压控制方程式（6）。控制框图如图2所示，其中下标d、q分别代表直轴、交轴分量。

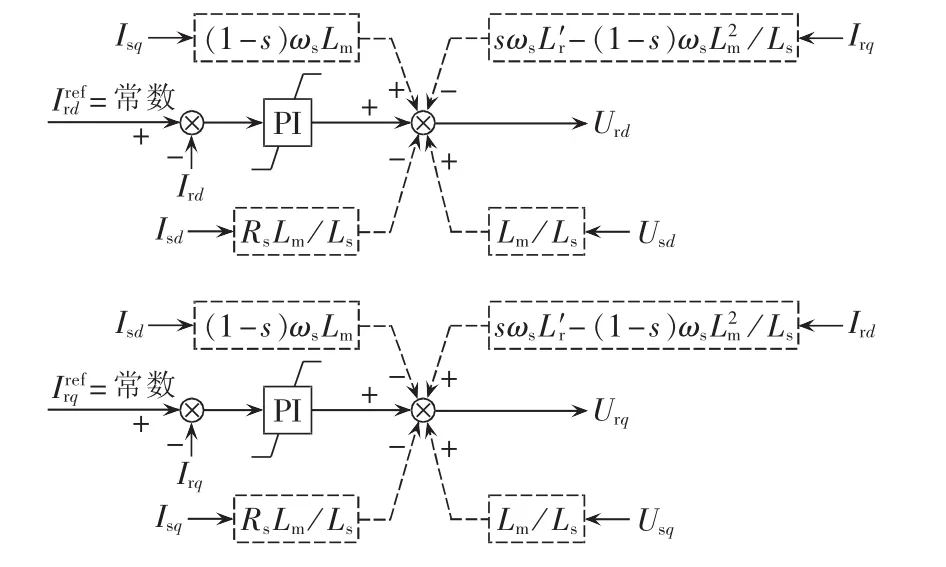
图2 计及定子磁链暂态的RSC恒定电流控制Fig.2 Constant current control of RSC considering stator flux transient

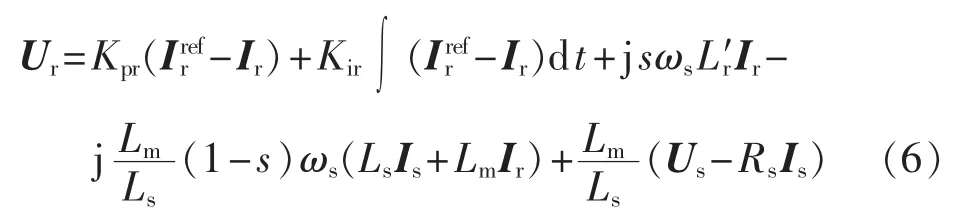
联立式（4）与式（6），可得转子电流的二阶微分方程表达式：

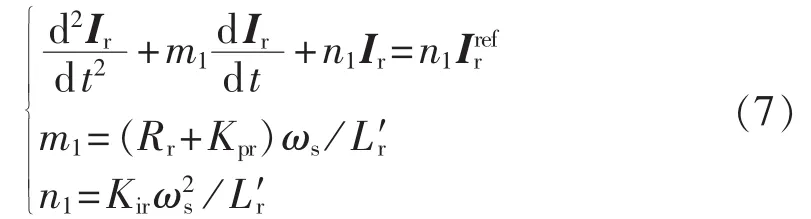
求解式（7），可得转子电流表达式：

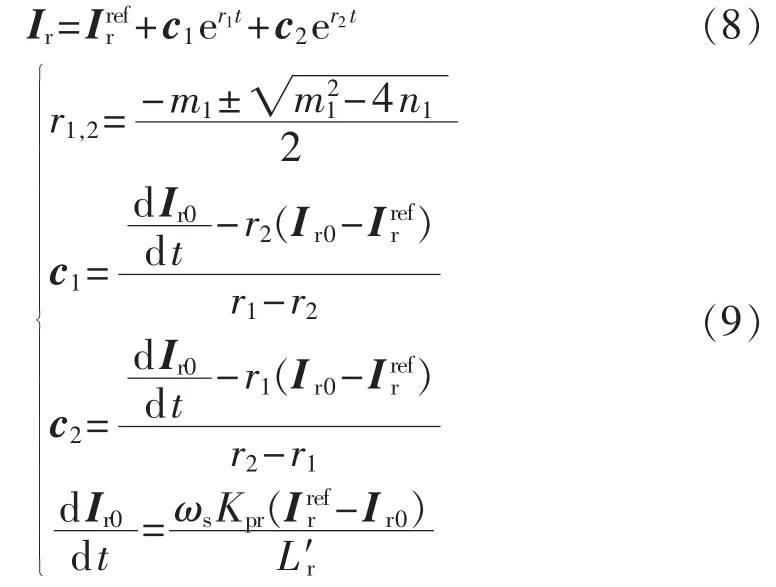
其中，下标0代表电压跌落初始时刻值。

随着PI环节的比例与积分系数增大，r1与r2减小，跟踪电流参考值的速度加快。若转子电流可在较短的时间内跟踪参考值，就可以在计算定子电流时将转子电流视作其参考值。

1.2 GSC恒定电流控制

由GSC电压方程式（10）与GSC控制方程式（11）推导出 GSC 电流式（12）—（14），其中 Kpg、Kig分别为GSC电流控制比例与积分环节系数。

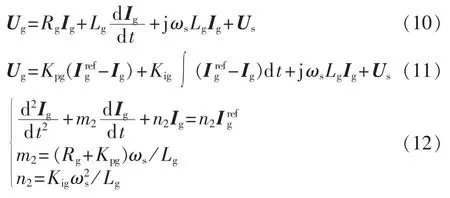
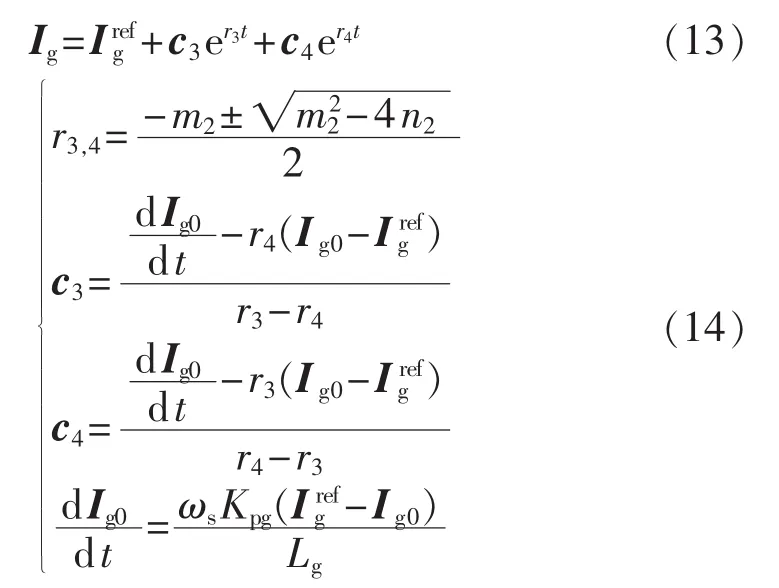
随着PI环节的比例与积分系数增大，r3与r4减小，跟踪电流参考值的速度加快。若GSC电流可在较短的时间内跟踪参考值，就可以在计算定子电流时将GSC电流视作其参考值。

1.3 定子以及机端故障电流表达式

在LVRT的过程中，将RSC电流与GSC电流视为其参考值，进而求解式（3），得到定子磁链、定子电流以及DFIG故障全电流：

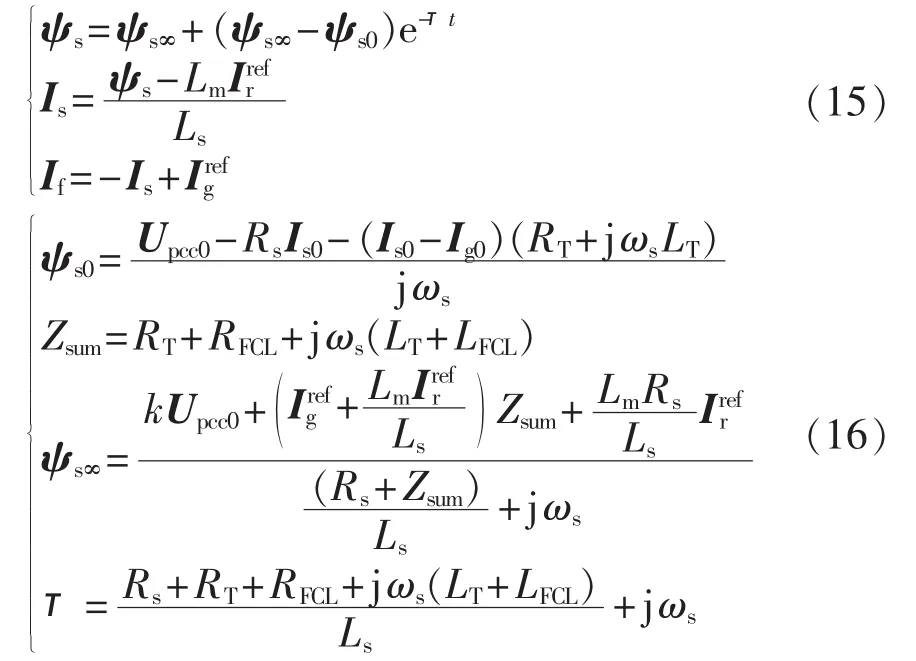
其中，k为PCC电压的跌落比例；ψs∞为电压跌落后定子磁链稳态值；τ为衰减时间常数；If为流入PCC的DFIG故障全电流；Zsum为出线变压器与FCL阻抗之和。

基于定子、RSC与GSC电流表达式，由式（2）可求解定子电压；由式（4）可求解RSC电压；由式（10）可求解GSC电压。其中RSC电压与转速相关，可取故障前DFIG初始转速近似处理。

值得注意的是，式（3）应在同一坐标系下求解。DFIG控制通常采用基于电压或磁链的dq轴定向控制，投入FCL初期定子电压与磁链相角随着电流振荡变化幅度较大，DFIG dq轴与电网xy轴夹角不断变化，此时dq轴恒定电流分量在xy轴上为变化量。通过坐标变换将dq轴与xy轴重合（放弃电压／磁链定向），既能确保故障电流解析表达的精度，也能够避免引起振荡。基于解析表达式同样可以通过设定RSC与GSC电流参考值调节DFIG输出功率。

2 采用FCL的DFIG LVRT控制参数选择

根据PCC电压与FCL投切状态将DFIG LVRT过程分为如下3个阶段，如图3所示。

a.电压跌落（t0—t1）。此时 FCL持续投入，DFIG RSC与GSC采用恒定电流控制。

b.电压恢复，FCL 投入（t1—tcut）。 此时，RSC 与GSC电流参考值恢复为初始运行状态的参考值。为了抑制电压回升对DFIG运行状态造成的冲击，此时FCL仍投入。

c.电压恢复，FCL 切出（tcut—tend）。 此时DFIG 运行参数趋于稳定。该阶段结束后DFIG重新采用电压／磁链dq轴定向，恢复正常运行状态。

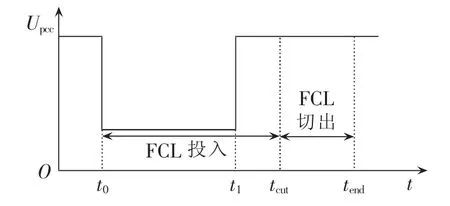
图3 LVRT过程中FCL控制策略Fig.3 Control strategy of FCL during process of LVRT

DFIG LVRT过程受RSC与GSC电流参考值、FCL阻抗与切出时间的影响。确定上述参数时，可分别在各参数可行范围内等间距取值，利用电流解析表达对比不同取值组合的LVRT效果，从而确定控制参数。在此过程中，需满足转速约束、定子电流约束、RSC与GSC的电压与电流约束等安全约束。

DFIG电磁转矩的振荡在影响DFIG输出功率的同时，还会缩短传动轴寿命。故以电磁转矩振荡ΔTe表征DFIG LVRT的效果：

其中，上标s1、s2、s3分别对应LVRT过程中3个阶段的电磁转矩稳态值。

3 算例分析

针对图1测试系统，取空气密度ρ=1.225 kg／m3，风机半径 R=32.13 m。Cp函数参数：c1=0.73，c2=121，c3=0.58，c4=0.002，c5=2.14，c6=13.2，c7=18.4，c8=-0.02，c9=-0.003［11］。 DFIG 额定功率 1.5 MW，额定电压 690 V。 Rs=0.007 06 p.u.，Ls=3.07 p.u.，Rr=0.005 p.u.，Lr=3.056 p.u.，Lm=2.9 p.u.，Rg=0.02 p.u.，Lg=0.1 p.u.，RT=0.02 p.u.，LT=0.08 p.u.，Kpr=1，Kir=0.1，Kpg=1，Kig=0.1。

3.1 RSC控制方式效果对比

DFIG机端串联FCL，在相同控制目标下采用不同的RSC控制策略，控制效果如图4所示（图中纵轴均为标幺值，后同，图4（b）中采用定子电压d轴定向与本文控制策略具有相同的转子电流波形）。

与不计定子磁链暂态结果相比，计及定子磁链暂态的RSC控制的冲击电流较小。与功率外环控制相比，取消了功率外环控制的功率追踪的速度更快，系统更容易趋于稳定；将DFIG dq轴与电网xy轴重合，相较定子电压d轴定向可以避免定子电压相角振荡对恒电流控制的影响，从而定子电流与功率的振荡较小。可见本文控制策略具有良好的LVRT效果。

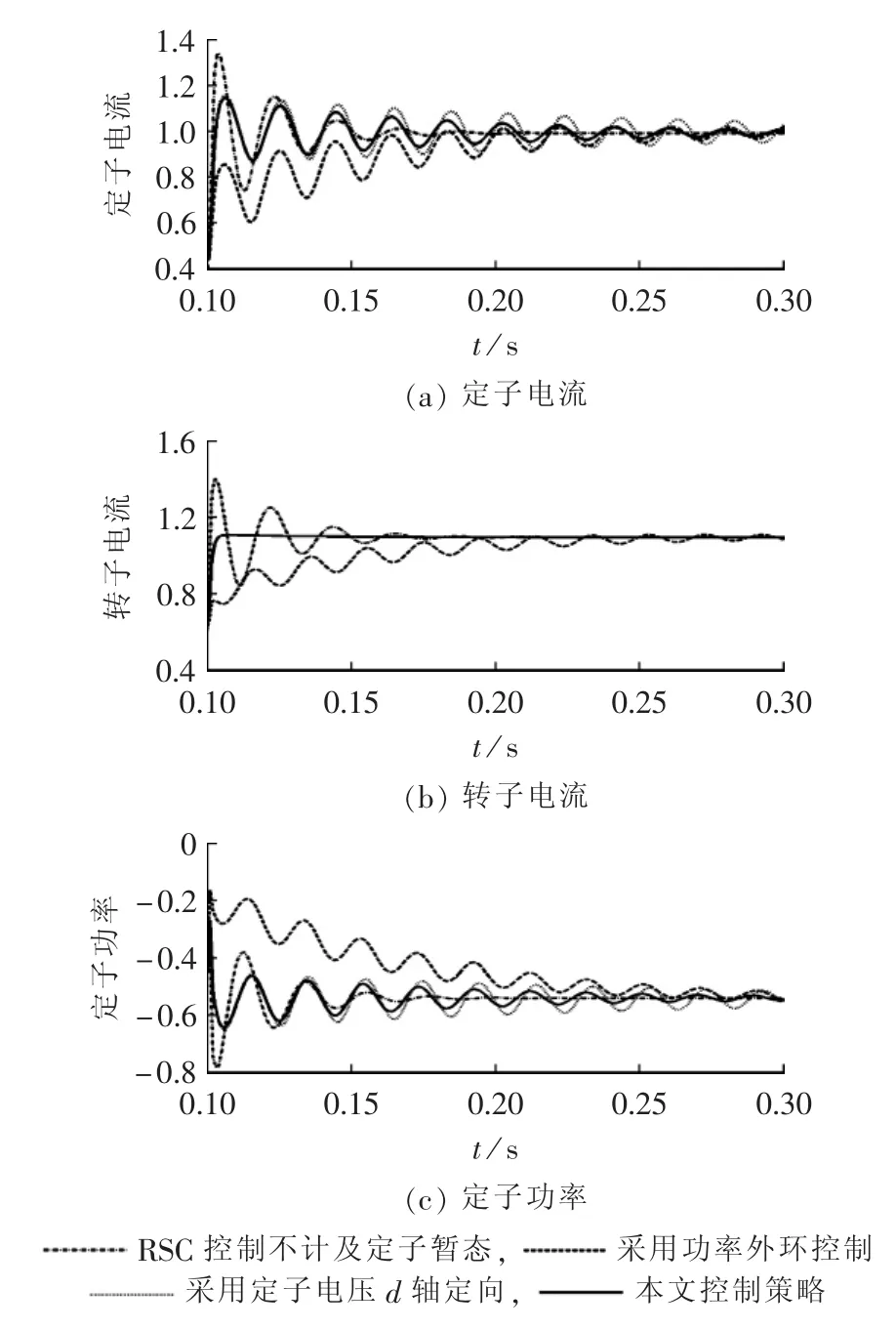
图4 采用FCL时不同控制策略下LVRT效果Fig.4 Effect of LVRT with FCL for different control strategies

3.2 FCL动作后DFIG电流解析表达

若在0.1～0.725 s内PCC电压由1 p.u.跌落至0.2 p.u.。在xy坐标系下RSC与GSC初始电流参考值分别为0.49-j0.33 p.u.与0.10+j0.01 p.u.，在LVRT的过程中分别取-0.3+j0.4 p.u.与0.3+j0.2 p.u.。FCL的阻抗取0.1+j0.2 p.u.，在1 s时FCL切出。由解析表达与动态仿真得到的DFIG定子电流、RSC与GSC的电压／电流如图5所示。

在恒定电流控制下，RSC与GSC可以迅速追踪电流参考值，满足本文解析模型的假设条件。定子电流、RSC与GSC电流／电压的解析表达与动态仿真结果的对比验证了本文提出的解析表达模型的精度。且本文的解析模型在电压跌落FCL投入、电压恢复FCL投入与电压恢复FCL切出3个阶段中皆能保证足够的精度，从而可以用于分析LVRT全过程。

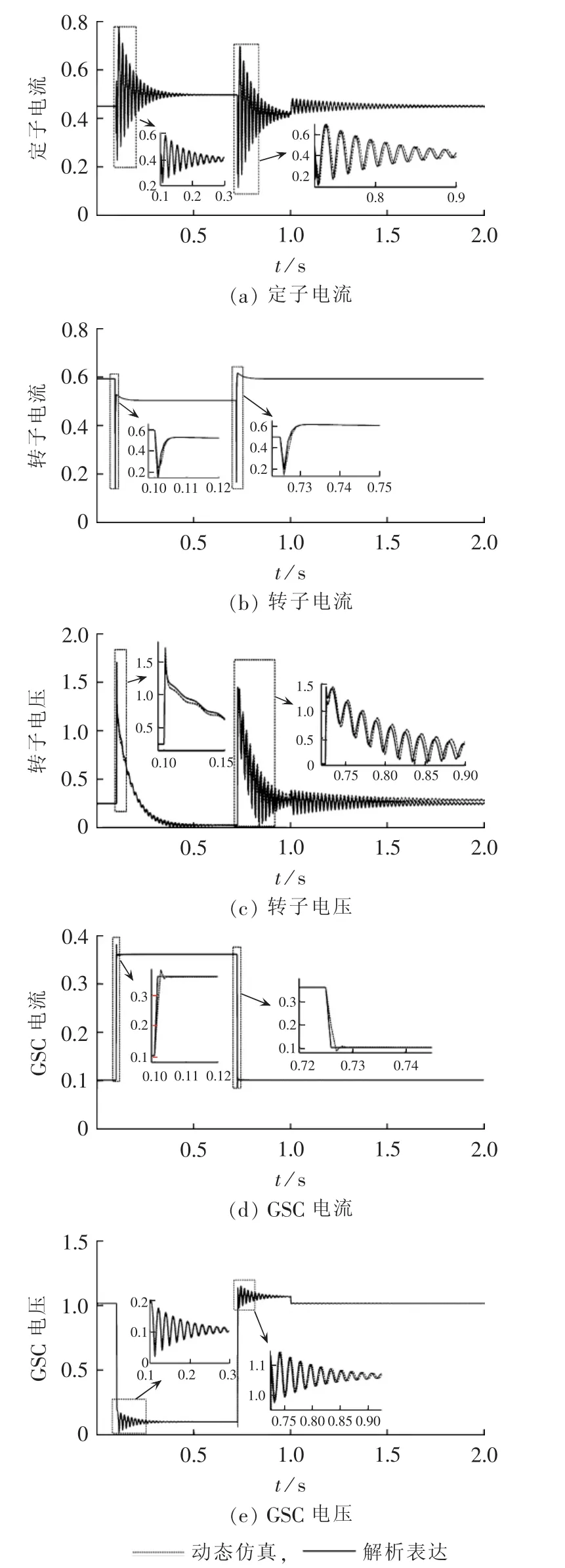
图5 动态仿真与解析表达结果Fig.5 Results of dynamic simulation and analytical calculation

3.3 控制参数选择

取 RSC 与 GSCdq 轴参考电流范围为［-2，2］p.u.，FCL 电阻与电抗范围为［0，1.2］p.u.，按间距 0.05 p.u.进行采样。取FCL切出时间范围为［1，1.2］s，按间距0.01 s进行采样。采用解析模型对比不同控制参数组合的LVRT效果。LVRT过程中定子、RSC与GSC电流需小于 2p.u.［12］，RSC 与 GSC 电压需小于 1.15p.u.［13］，DFIG 无功电流需满足 Iq＞ 1.5（0.9-k）［14］。

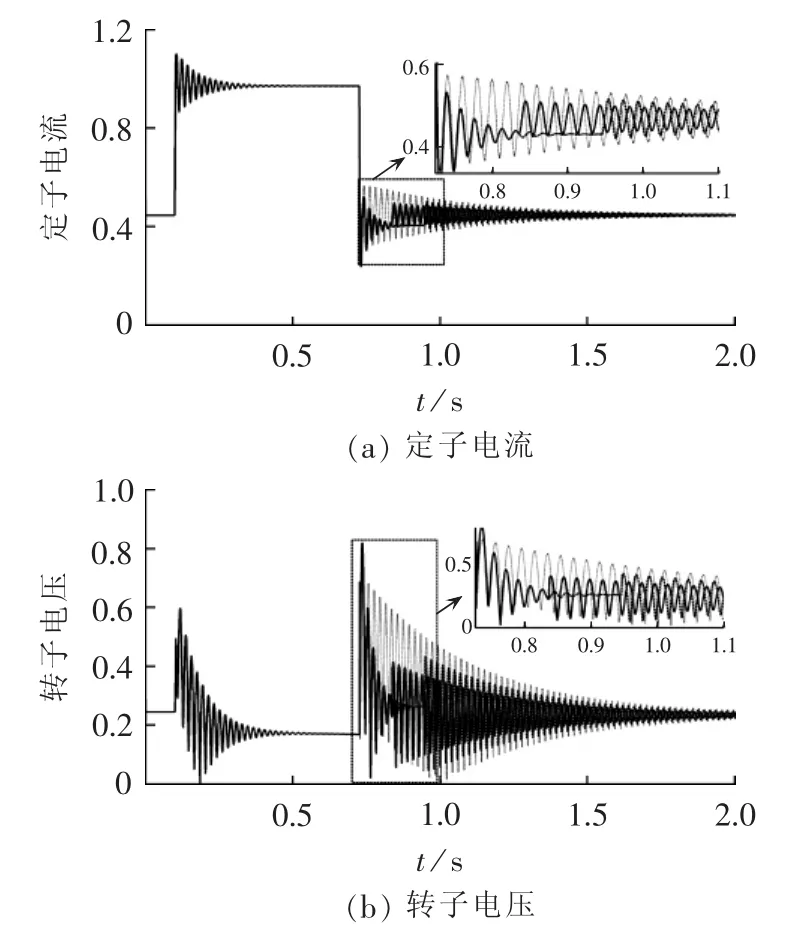
基于故障电流的解析表达，取RSC电流参考值为 1.1－j0.25 p.u.，GSC 电流参考值为 0.3－j1.2 p.u.，FCL阻抗值为0.35+j0.25 p.u.，并在电压恢复后立即切除FCL，DFIG的电磁转矩振荡最小。然后采用动态仿真验证所选取参数的控制效果，如图6与图7所示。结果表明，基于解析模型选取的控制参数，抑制定子电流、转子电压与电磁转矩振荡的效果更好一些。

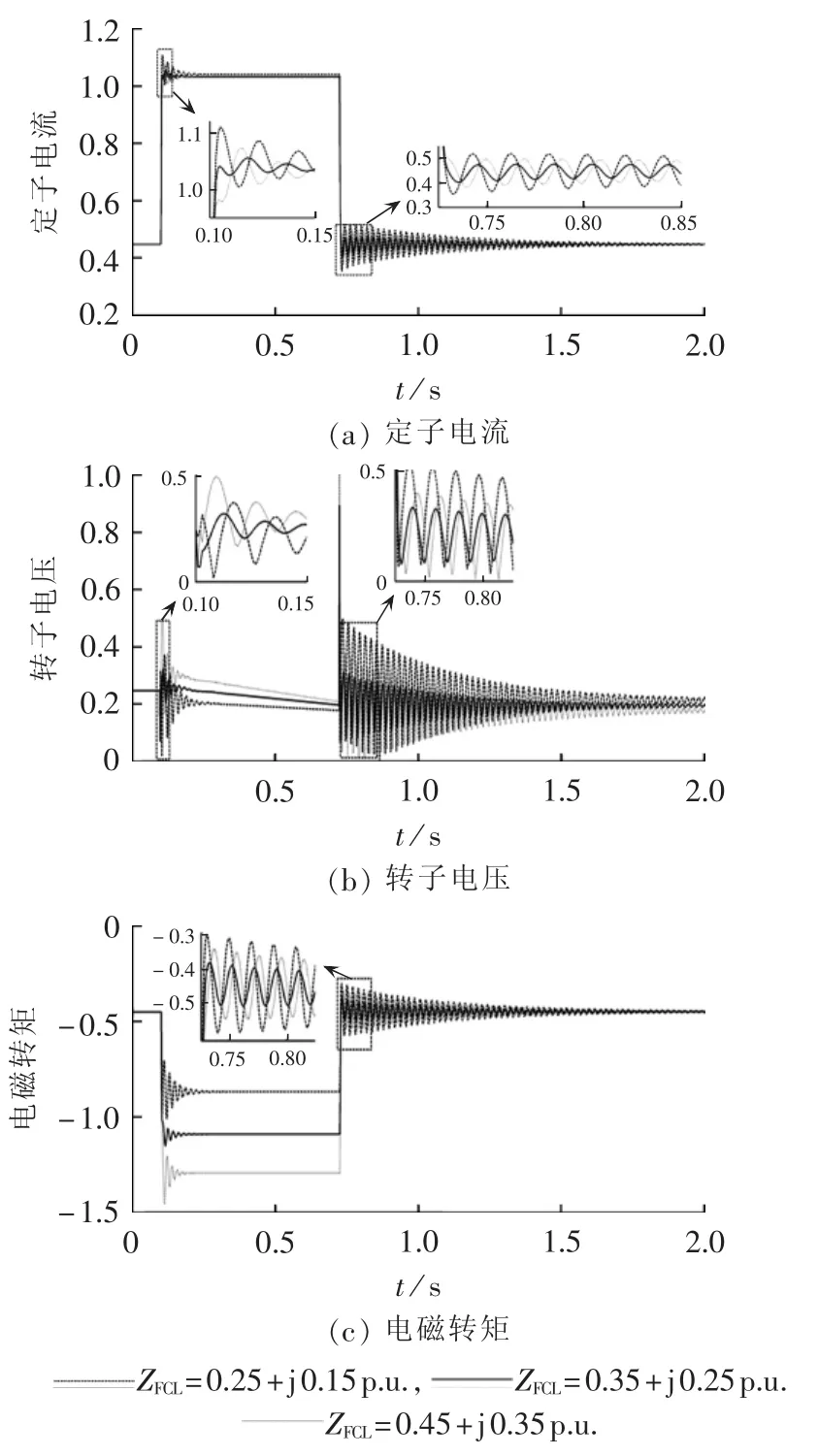
图6 不同FCL阻抗值的LVRT效果Fig.6 Effect of LVRT for different FCL impedances

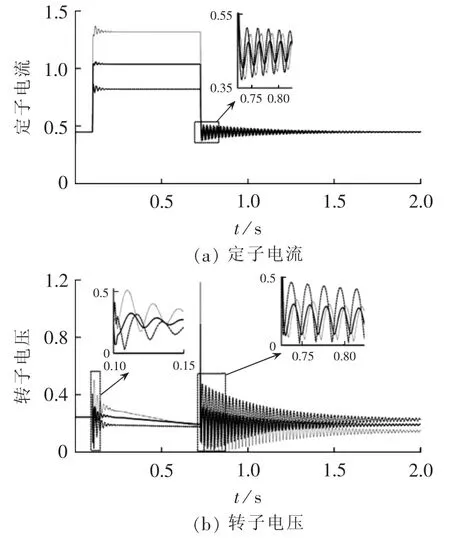
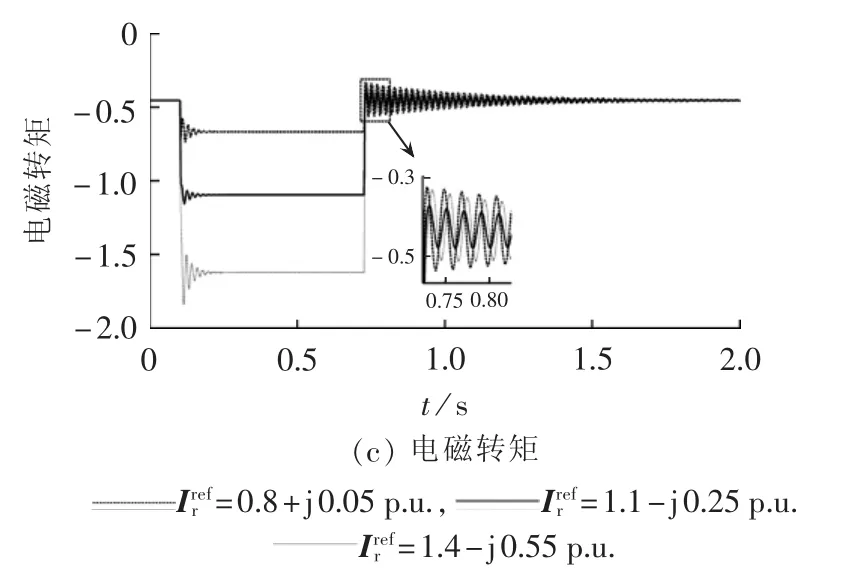
图7 不同RSC电流参考值的LVRT效果Fig.7 Effect of LVRT for different RSC current references

图6中当FCL阻抗大于所选取值时，定子电流与电磁转矩的振荡反而更剧烈，这与通常的认知相悖。原因在于，电磁振荡是由定子磁链振荡引起的，增大阻抗可增大直流磁链分量的衰减系数，促进振荡衰减。然而定子磁链稳态值受RSC、GSC电流参考值与FCL阻抗大小共同影响。由于优化取值下定子磁链初始值与稳态值相差（直流磁链）较小，在FCL阻抗较小的条件下产生的电磁转矩振荡仍然较小。

在电压恢复的过程中，DFIG的暂态响应还受FCL切出时间的影响。若过早切出，电压回升产生的暂态电流振荡较为剧烈；若过晚切出，FCL的切出会产生振荡，不利于DFIG尽快回归正常运行状态。其他条件不变，FCL阻抗值取0.1+j0.1 p.u.，选取FCL切出时间为0.24 s。不同切出时间下DFIG的暂态响应如图8所示，所选切出时间更便于DFIG尽快地恢复正常运行。

对比图6—8，可得FCL阻抗较大时对应的切出时间较短。主要原因是：较大阻抗值时FCL切出后暂态过程较为剧烈，为了尽快恢复DFIG正常运行状态，需要尽早切出；LVRT过程中较大阻抗值的FCL两端电压也较大，尽早切出还可以抵消电压回升的影响。

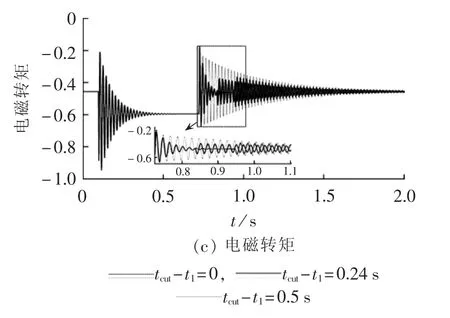
图8 FCL不同切除时间的的LVRT效果Fig.8 Effect of LVRT for different tripping time of FCL

4 结论

基于RSC与GSC恒定电流控制策略，采用FCL实现DFIG故障穿越，本文提出了DFIG故障电流的解析表达以及RSC与GSC电流参考值、FCL阻抗与切出时间等控制参数的选取方法，得到以下结论。

a.故障后启动恒定电流控制时，由于考虑了定子磁链暂态，具有较小的冲击电流；放弃了功率外环控制，从而具有较快的跟踪速度；将dq轴与电网xy轴重合避免了定子电压相角振荡的影响，转子电流与功率振荡较小。

b.较大的FCL阻抗将加速直流磁链衰减，而直流磁链大小受FCL阻抗和RSC、GSC电流参考值的影响，需综合考虑确定FCL阻值以抑制电磁转矩振荡。

c.电压恢复阶段DFIG暂态过程受FCL切出时间影响。FCL过早切出，电压回升会产生较大的冲击，FCL过晚切出不利于DFIG尽快回归正常运行状态。FCL阻抗值较大，LVRT过程中电压较大，尽早切出可以抵消电压回升，使DFIG尽快回归正常运行。

参考文献：

［1］李生虎，安锐，许志峰，等.混合风电场中PMSG协助感应发电机低电压穿越［J］. 电力自动化设备，2015，35（2）：21-27.LI Shenghu，AN Rui，XU Zhifeng，et al.Coordinated LVRT of IG and PMSG in hybrid wind farm［J］.Electric Power Automation Equipment，2015，35（2）：21-27.

［2］徐海亮，章玮，贺益康，等.双馈型风电机组低电压穿越技术要点及展望［J］. 电力系统自动化，2013，37（20）：8-15.XU Hailiang，ZHANG Wei，HE Yikang，et al.A review on low voltage ride-through technologies and prospect for DFIG wind turbines［J］.Automation of Electric Power Systems，2013，37（20）：8-15.

［3］郑涛，魏旭辉，李娟，等.PI控制参数对双馈风电机组短路电流特性的影响分析［J］. 电力自动化设备，2016，36（7）：15-21.ZHENG Tao，WEI Xuhui，LI Juan，et al.Influence of PI control parameters on short circuit current characteristics of DFIG ［J］.Electric Power Automation Equipment，2016，36（7）：15-21.

［4］熊小伏，欧阳金鑫.电网短路的双馈感应发电机转子电流的分析与计算［J］. 中国电机工程学报，2012，32（28）：114-121.XIONG Xiaofu，OUYANG Jinxin.Analysisandcalculation of rotor currents for doubly-fed induction generators under short circuits in power grids［J］.Proceedings of the CSEE，2012，32（28）：114-121.

［5］张文娟，马浩淼，张国慨，等.基于转子串联电阻的双馈风力发电机低电压穿越［J］. 电力自动化设备，2015，35（12）：28-33.ZHANG Wenjuan，MA Haomiao，ZHANG Guokai，etal.Low voltage ride-through of doubly-fed induction generator based on rotor series resistor［J］.Electric Power Automation Equipment，2015，35（12）：28-33.

［6］CHEN L，ZHENG F，DENG C，et al.Fault ride-through capability improvementofDFIG-based wind turbine by employing a voltage-compensation-type active SFCL［J］.Canadian Journal of Electrical and Computer Engineering，2015，38（2）：132-142.

［7］GAO W，WANG G，NING J.Development of low voltage ridethrough control strategy for wind power generation using real time digital simulator［C］∥Power Systems Conference and Exposition.Seattle，WA，USA：IEEE，2009：1-6.

［8］HOWARD D F，LIANG J，HARLEY R G.Short-circuit modeling of DFIGs with uninterrupted control［J］.IEEE Journal of Emerging and Selected Topics in Power Electronics，2014，2（1）：47-57.

［9］HU J，HE Y.Dynamic modelling and robust current control of wind-turbine driven DFIG during external AC voltage dip ［J］.Journal of Zhejiang University-Science A，2006，7（10）：1757-1764.

［10］SADI M A H，ALI M H.A fuzzy logic controlled bridge type current limiter for transient stability augmentation of multimachine power system［J］.IEEE Transactions on Power Systems，2016，31（1）：602-611.

［11］HEIER S.Grid integration of wind energy conversion systems［M］.Chichester，UK：Weily，1998：31-43.

［12］XIAO S，GENG H，ZHOU H，et al.Analysis of the control limit for rotor-side converter of doubly fed induction generator-based wind energy conversion system under various voltage dips［J］IET Renewable Power Generation，2013，7（1）：71-81.

［13］LIU S，BI T，JIA K，et al.Coordinated fault-ride-through strategy for doubly-fed induction generators with enhanced reactive and active power support［J］.IET Renewable Power Generation，2016，10（2）：203-211.

［14］全国电力监管标准化技术委员会.风电场接入电力系统技术规定：GB／T 19963—2011［S］. 北京：中国标准出版社，2011.