基于GBFA求解复微分方程①

张志敏

(阳光学院基础教研部，福建福州350015)

基于GBFA求解复微分方程①

张志敏

(阳光学院基础教研部，福建福州350015)

为了提高传统方法在求解二阶以及高阶复微分方程之时搜索能力差、后期收敛速度较慢以及难以得到的缺陷，基于传统的免疫算法(generate and test)和BFA(Bacterial Foraging Algorithm，细菌觅食算法)的相关概念，融合半解析解的相关思想，构建一种新的算法GBFA(Generate Bacterial Foraging Algorithm)，并基于此方法进行求解实验，结果表明该方法具有极高的收敛速度，可以得到二阶以及高阶复微分方程解析表达式.

细菌觅食算法，全局搜索，半解析法，解析表达式

0 引言

复微分方程是数学、工程实践中广泛存在的棘手问题.类型多样化是传统数值计算方法的一大特征，具体包括弦截法、单形调优法、对分法及复形调优法等[1,2].然而方程特点对上述数值计算方式造成了较大的干扰，在初值不同的情况下会使计算结果产生显著的差异，因此传统数值法不具有良好的通用性，且精确程度不高.所以广大研究学者结合经验，针对实际问题对计算法进行选取，但也存在主观性较强的问题，所以不能在工程中普遍运用数值计算法.

二十世纪九十年代，K.M.Passino等提出了Bacterial Foraging Algorithm[3]，该算法在求解复微分方程之时，可以很好地探寻解复微分方程的根.Bacterial Foraging Algorithm作为实用性较强的数学工具，拥有较强的通用性，且迭代格式简便，能够普遍用于解决、处理(非)连续性问题，方便进行学习和应用[4,5].然而，Bacterial Foraging Algorithm需要运用较长的时间进行后期收敛，效果不够理想，无法达到小范围的收敛效果[6,7].李闯利用解析解的思想对于BFA进行了部分优化，提高了BFA的收敛精度和寻优速度，可以得到方程的解析表达式，但是李闯针对的是特定问题，没有系统探讨BFA，更没有涉及BFA的搜索能力[8]；Tang W J[9]将繁殖算子的思想融合进入BFA，提高了BFA的寻优能力，但是却牺牲了精度和寻优的速度.

现有的针对BFA的研究成果往往针对BFA的寻优能力和搜索能力进行优化，无法兼顾寻优速度和收敛精度.本研究结合BFA算法的复制、趋向性及迁移这三个关键操作过程，融合免疫算法(generate and test)的相关思想，研究出全新的BFA优化算法，即GBFA算法(Generate Bacterial Foraging Algorithm).在该算法中，首先能够对趋向性操作过程下的步长进行非固定转变，步长要根据运算而变化，并针对趋向性操作步长构建动态更新机制；其次，要对复制操作过程借助免疫算法进行更换，筛选细菌群落，将低适应度细菌更换成高适应度细菌，或对高适应度细菌进行复制；然后，高适应度个体在迁移操作过程被驱散率是零，剩余个体被驱散率是Ped.并利用C++开发计算程序，与传统的计算方法相比较，验证Generate Bacterial Foraging Algorithm的对于求解复微分方程的适应性.

1 问题描述

有一复微分方程

f(h(x))=0.

(1)

可以将式(1)转化为

g(h(x))=f(h(x))2.

(2)

区间范围下，公式(2)的最小值点为公式(1)的解，若g(x)的极小值是零，则相应函数h(x)就是式(1)的根的解析表达式.

2 算法简介

2.1GBFA算法的基本思想

BFA中第i次的步长为

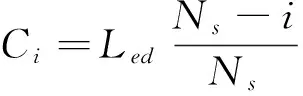
(3)

其中，BFA虚拟的细菌群落内细菌游动次数的最大值是Ns，细菌游动的初始步长是Led，初始步长均各次移动步长要大.运算初期的i值相对不大，而第i次步长Ci较大，能够使搜索速度大大提升，改善了运算效率.在运算不断推进的过程中，i值会不断变大，第i次步长Ci出现不断减小趋势，这样就能够使后期运算过程中收敛精度提升.

借助构建的趋向性操作步长动态更新机制，可以累计加和群落内全部细菌的适应度，按照由大到小的次序建立细菌序列.复制前部分细菌序列的m(%)，复制次数为n，删除序列内的其它细菌，则m、n能够表示成

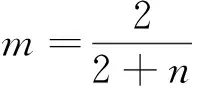
(4)

结合上述公式，原细菌群落即为群落细菌的m，这样能够使群落的觅食能力得到显著增强.细菌菌落的变异及繁殖过程为：(1)以高适应度为标准，对细菌群落内的细菌进行挑选，挑选出的细菌标成克隆群体A；(2)繁殖克隆群体A，使其形成群体B.

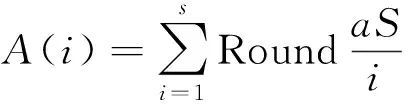
(5)

其中，细菌群落的总数量表示成S，四舍五入函数表示成Round；运算所得的克隆群体数目为A(i)；第i次运算表示成i，克隆系数是a.通过下述方式来标准化处理适应度F，能够使运算更加简便化.

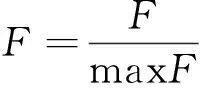
(6)

公式中最大值函数是max.

(3)变异处理细菌群体B，生产群体C：

B(i)=B(i)+βrandomn(C)，

(7)

其中，随机函数表示成random，变异概率是β，运算所得的克隆群体数量是B(i).详细运算方式如

β=e-F(n-i+1).

(8)

参考上述公式能够得知：细菌个体适应度如果较高，则变异概率越大，二者成正比关系.交叉法的公式为

H=B(x1)-B(x2)+B(x3)-B(x4).

(9)

式(9)中，克隆群体内细菌的四大类型为x1、x2、x3和x4.在细菌群体内融入克隆群体，可以构建出新细菌群体

D=B+C.

(10)

(4)在细菌群体D中复制前m(%)的细菌群落，复制次数为n，剔除其它细菌.

基于BFA算法下，将迁移概率设置为Ped，若迁移概率Ped大于随机数，则需要迁移细菌，从而有效摆脱陷入局部最优解的状况.然而该方式也存在缺陷，由于全部细菌均存在迁移概率，因此适应度不同的细菌均存在被迁移的可能性.在GBFA算法中的迁移操作过程，适应度最高细菌个体被驱散概率是零，剩余个体被驱散率是Ped，由此能够加快搜索的速度，减小耗时.

参考上述理论，得出GBFA算法的流程，详见图1.

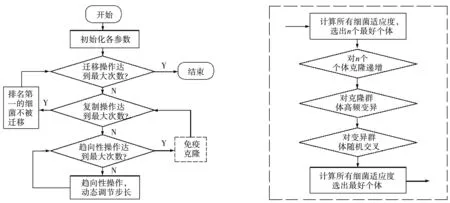
图1 GBFA算法的流程示意图

2.2 GBFA算法的敛散性

在BFA算法的敛散性方面，DASGUPTA开展了深入的分析[11,12]，然而并未研究BFA算法下细菌群落中的个体间也会彼此影响，未对影响关系进行模拟.本文中的GBFA算法基于原算法的概念，融入了免疫算法，因此还应对GBFA算法的敛散性进行验证.

结合李涛的分析成果[13]：抗体种群为A0，抗体空间几何表示成I*，经运算的最优解数目是v(A(k))，最优解个数是B*

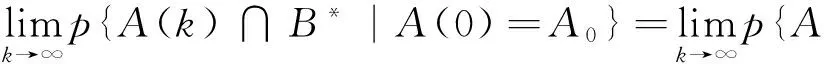
(11)

化简得到

(12)

因此1是GBFA算法收敛到最优解集的概率.若算法迭代数量符合特定标准，算法就会收敛.

将免疫算法融合到GBFA算法中，针对细菌抗体种群A0则有

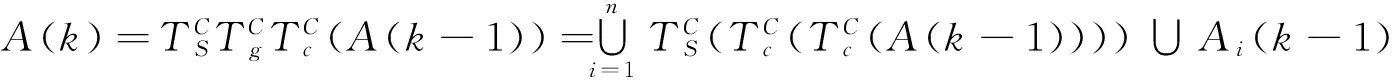
(13)

其中，k=1,2…,第k次操作时，细菌i的位置为Ai(k)，Ai(k-1)经过变异和克隆后能够得到Ai(k).通常采用下述方式进行简便表示

P0(k)=P{v(A(k))=0}=P{A(k)∩B*}，

(14)

则有

P0(k+1)=P{v(A(k+1))=0|v(A(k))≠0}P{v(A(k))≠0}，

+P{v(A(k+1))=0|v(A(k))=0}P{v(A(k))=0}，

(15)

因为

P{v(A(k+1))=0|v(A(k))≠0}=0，

(16)

则有

P0(k+1)=P{v(A(k|+1))=0|v(A(k))=0}P{v(A(k))=0}，

(17)

又因为

(18)

P{v(A(k+1))≥1|v(A(k))=0}≥≻0，

(19)

所以

P{v(A(k+1))=0|v(A(k))=0}=1-P{v(A(k+1))≠1|v(A(k))=0}≤1-0，

(20)

故而

0≤P0(k+1)≤…≤(1-)k+1P0(0)，

(21)

因为

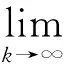
(22)

0≤P0(0)≤1，

(23)

所以

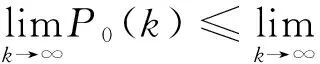
(24)

所以

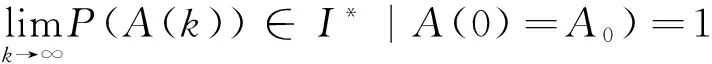
(25)

综上所述，GBFA以概率1收敛.

3 半解析解的思想

根据李闯[8]使用的半解析法的思想，将计算机计算解释为计算机代数系统.在计算机代数系统之中，每一个数值项以及变量都以字符的形式储存，可以以字符串为基本运算单位.但其收敛与否应受到GBFA算法的影响.

4 计算仿真

利用上述思想，编制GenerateBacterialForagingAlgorithm的C++程序GOS，利用GOS进行计算.

4.1 二阶及高阶复微分方程

算例1 求解y″-6iy′=-i{6(1-3 ix)x+2 (19 i +6x) cosh[(6- ix)x]+4 (3 i +x)2 sinh[(6- ix)x]}.利用GOS，得到

y=-ix3+sin(x2+6ix).

(26)

算例2 求解y(5)+ iy′= 720 i -(16 807+7 i) e7x+720x-30x4+6 ix5,利用GOS，得到

y=x6-e7x+6ixs.

(27)

算例3 求解

+9ix(20(9x6-2)sin(x3)+3(9x6-80)x3cos(x3))540e(3x2+i)x2

+60ex3+ix(3x2+i)3x+ex(3x2+i)5+60ex3+ix(3x2+i)2

-3i(18x3sin(x3)+(9x6-2)cos(x3))+18ex3+ix(3x2+i)x

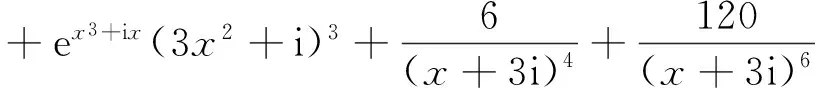
利用GOS，得到

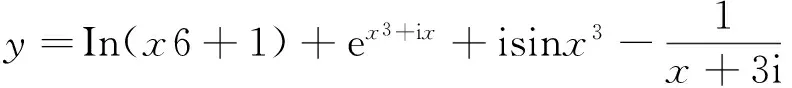
(28)

通过算例1、算例2和算例3可知，GenerateBacterialForagingAlgorithm可以很好的求解出二阶微分方程和高阶微分方程的解析表达式，说明GenerateBacterialForagingAlgorithm对于该类问题给予极好的适用性.

4.2 计算时间

算例4 利用三种方法分别计算算例3

利用文献7中FAC算法、SPSO算法进行计算，同GenerateBacterialForagingAlgorithm对局部根进行搜索耗时开展对照研究，具体如表1所示.

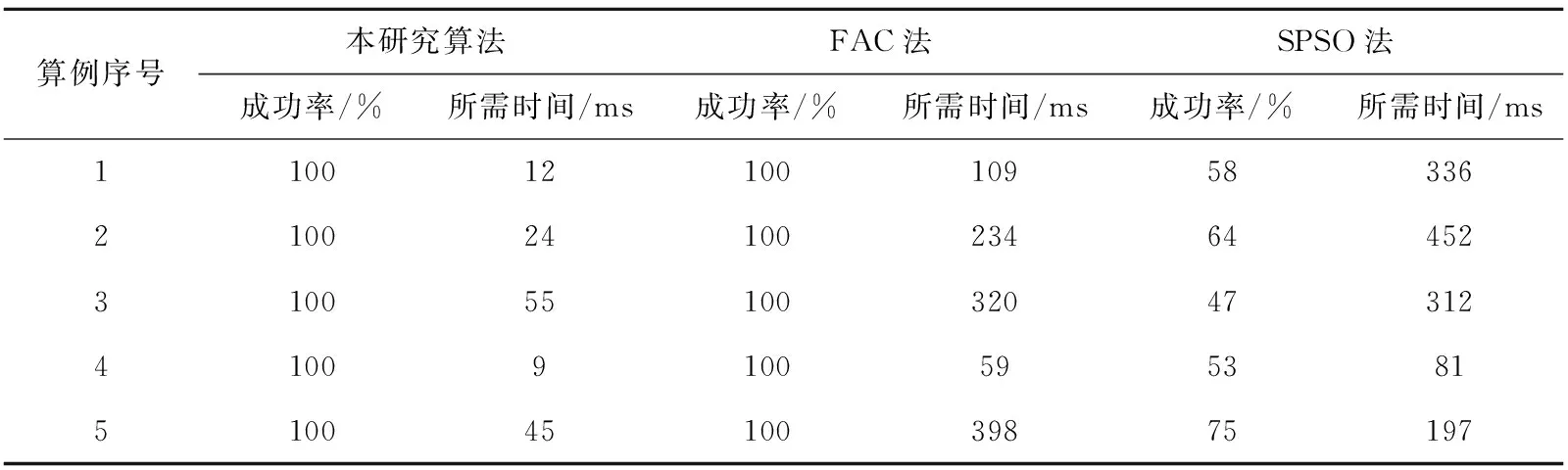
表1 本研究法、FAC法及SPSO法的对比结果

结合上表得知：GenerateBacterialForagingAlgorithm的耗时最大为55ms，FAC法、SPSO法耗时最大分别为398ms、452ms.GenerateBacterialForagingAlgorithm耗时仅为FAC法、SPSO法的13.8%、12.2%；GenerateBacterialForagingAlgorithm的平均耗时最大为29ms，FAC法、SPSO法耗时最大分别为224ms、275.6ms.GenerateBacterialForagingAlgorithm的平均耗时仅为FAC法、SPSO法的12.9%、10.5%；GenerateBacterialForagingAlgorithm和FAC法的运算成功率都是百分之百，而SPSO法的运算成功率为47%-75%，这就表示GenerateBacterialForagingAlgorithm是一种计算成功率高，耗时极短的计算方法.

5 结论

基于BFA算法的复制、趋向性及迁移三大操作环节，融合免疫算法(generateandtest)的相关思想，研究出全新的BFA优化算法GBFA算法，该算法的优点可总结如：(1)融合了半解析解思想，基于计算机代数系统的GBFA可以求解出二次微分方程以及高阶微分方程的解的表达式；(2)相对于现有的计算方法，GBFA的计算耗时较短，但收敛效果远远高于其他两种常用的传统复微分方程求解方法.

[1]BianchiniM,FanelliS,GoriM.OptimalAlgorithmsforWell-ConditionedNonlinearSystemsofEquations[J].IEEETransactionsonComputers, 2001, 50(7):689-698.

[2] 陈子仪,康立山,胡欣.遗传算法在方程求根中的应用[J].武汉大学学报：理学版,1998，44(5):577-580.

[3]LiuY,PassinoKM.BiomimicryofSocialForagingBacteriaforDistributedOptimization:Models,Principles,andEmergentBehaviors[J].JournalofOptimizationTheory&Applications, 2002, 115(3):603-628.

[4]EberhartR,KennedyJ.Anewoptimizerusingparticleswarmtheory[C].//MicroMachineandHumanScience1995.ProceedingsoftheSixthInternationalSymposiumonIEEE, 1995.

[5] 刘华蓥.粒子群优化算法的改进研究及在石油工程中的应用[D].大庆：东北石油大学,2012.

[6] 田明俊,周晶.岩土工程参数反演的一种新方法[J].岩石力学与工程学报,2005,24(9):1 492-1 496.

[7]JingKE,QianJX,QiaoYZ.AModifiedParticleSwarmOptimizationAlgorithm[J].JournalofCircuits&Systems, 2003, 26(2):151-155.

[8] 王俊奇, 李闯, 董晔.Bishop法的半解析解及其广义数学模型[J]. 水利与建筑工程学报, 2015(6):123-128.

[9]TangWJ,LiMS,HeS,etal.OptimalPowerFlowWithDynamicLoadsUsingBacterialForagingAlgorithm[C].//PowerSystemTechnology2006.InternationalConferenceon.IEEE, 2006.

Solving Complex Differential Equations Based GBFA

ZHANG Zhi-min

(Basic Teaching and Research Department, Sunshine College，Fuzhou 350015，China)

In order to enhance the traditional methods in solving when searching for second order and higher-order complex differential equations of the poor, the latter is difficult to obtain and slow convergence defects, based on traditional immune algorithm (generate and test) and BFA (Bacterial Foraging Algorithm, bacterial foraging algorithm) related concepts, integration of related thought semi-analytical solution to construct a new algorithm GBFA (Generate bacterial foraging algorithm), and solved by experiments based on this method, the results show that this method has a very high rate of convergence, you can be second order and higher-order complex differential equations analytical expressions.

bacterial foraging algorithm，global search，semi-analytical method，analytical expressions

2016-12-10

福建省自然科学基金项目(2012J01256)资助

张志敏，E-mail：crystal_100@sohu.com

O241.3

A

1672-6634(2017)01-0033-05