基于图像信息熵的随机数可视化表达

白迪+田茂+陈小莉+刘美华+谢桂辉

摘 要：为了提高严格受控环境下信息隐写算法的安全性和鲁棒性，基于网络图像大数据提出了一种针对小容量负载的图像零隐写隐秘通信算法.在构建算法所需的完备库时，首先根据网格描述符对图像进行单元熵的提取以形成熵矩阵，然后提取熵矩阵的特征值以降维从而减少计算量，最后根据量化算法将特征值量化为一组随机数以构建完备库.实验结果表明：该算法由于没有改变原始载体图像，所以对于抗击已知原始载体的统计、比对分析和尺度缩放攻击、旋转攻击具有非常好的效果，在尺度缩放和旋转攻击的实验中数据恢复率达到95%以上.在安全级别高、受监控程度严格、容量较小的隐匿通信中，比如对称密码系统密钥的交换，具有重要的应用价值.

关键词：大数据；信息熵；信息隐写；零隐写；隐秘通信

中图分类号：TN919.8 文献标志码：A

Image-entropy-based Visual Expression of Random BAI Di1， TIAN Mao1， CHEN Xiaoli1，LIU Meihua1，XIE Guihui2

（1.Electronic Information School， Wuhan University， Wuhan 430072， China；

2.School of Automation， China University of Geosciences， Wuhan 430074，China）

Abstract：In order to improve the security and robustness of information hiding method in strict monitoring environment， based on network image big data， this paper proposed a new covert communication algorithm of image zero steganography for payload with low capacity. When constructing the complete library， the first step was to extract the entropy to form the entropy matrix according to the grid descriptor， and the characteristic values of the entropy matrix were then extracted to reduce the amount of computation. Finally， the characteristic values were quantified as a set of random number to build a complete library according to the quantization algorithm. The experimental results show that in statistical analysis， comparison analysis， dimension scaling attack， and rotation attack， the proposed algorithm can achieve good performance because of its none-modifying on carrier image. Particularly， in the test of dimension scaling attack and rotation attack， the rate of data recovering can be over 95%. The algorithm can be very valuable in high security， strict monitoring， and low capacity covert communication： for example， the key exchange of symmetric encryption system.

Key words：big data； information entropy； information hiding； zero steganography； covert communication

近年來，国家安全问题日益突出，自从2013年斯洛登“监控门”曝光事件以后国防安全被提到了新的高度，其中潜伏在境外的情报人员的安全问题备受关注.如果采用传统的密码加密方式与外界进行信息交流可能会提高监控方的警惕，进而使得情报人员的信息和人生安全受到更大的威胁.信息隐藏技术因为可以一定程度上消除监控方的警觉而引起更多相关研究者的兴趣.文献[1]采用了将隐秘信息经过加密后嵌入到载体图像像素的最不重要位中的方法；文献[2]提出了一种基于灰度级修改和多级加密的算法，该算法提高了载密体的图像质量并且具有多个安全等级，给隐匿分析者提出了更大的挑战；文献[3]提出了一种基于游程长度的信息隐藏算法，该算法最多改变二值图像黑白交界处的一个像素便可隐藏1比特的信息.文献[4-5]从频域的角度对信息隐匿进行了探讨.虽然上述各种信息隐匿研究都取得了不错的效果，但是其最终都是以修改原始载体的方式来达到隐匿通信的目的，事实上这种“嵌入式”的隐匿通信一定程度上并不安全.因为随着搜索引擎技术的发展，监控方可以很容易地获取到原始载体图像，进而能够通过对载密图像和原始载体图像进行逐像素点比对分析以判断其是否被嵌入秘密信息.

随着隐写技术的发展，零隐写技术的出现很好地解决了这个问题.零隐写术是指在完全不改变图像信息的前提下通过提取图像的特征，将其与隐秘信息进行融合的方式来实现隐秘通信.文献[6-7]阐述了零隐写术的具体实现的过程以及相应的鲁棒性、安全性测试的结果.零隐写术由于完全没有改变原始图像，所以具有极好的不可见性，对于抗击统计分析具有非常好的效果.但是零隐写术的实现过程中会产生额外的辅助信息，比如文献[6]中提出的零隐写算法会产生额外的Data key Kd，其需要占用专门的隐秘信道来传递，这给实际应用带来诸多不便.而本文提出的零隐写隐秘通信算法借助大数据的工具从互联网中搜索出热门图片，通过算法将其与负载信息建立映射关系，利用图片的特征信息直接表达负载信息，其不需要占用专门的隐秘信道来传递秘钥信息，从而提高了零隐写技术的实用性，而且凭借完全不修改原图和网络热门图片的特点，本文算法在削弱监控方的警觉方面具有天然的优越性，从而实现在监控严格、安全级别高以及负载较小的应用环境下真正安全的隐匿通信.

1 IEBVER算法

IEBVER（基于图像信息熵的随机数可视化表达，Image-Entropy-Based Visual Expression of Random）算法总体系统框图如图1所示，它包括完整的发送端处理流程、通信信道和接收端处理流程.在发送端随机数首先经过RSA算法加密处理变成相应的密文信息.由于消息在经过网络传递的过程中会受到噪声干扰的影响，从而造成二进制信息的误码，本文将Turbo编码技术加入到随机数发送端的处理流程中.经过Turbo编码后的信息即为发送端的业务信息.大数据采集是基于Java环境开发的一套网络热门图片大数据采集系统，其基于并行处理[8]架构将网络图像大数据进行搜索、清洗和过滤.映射算法用于从网络搜索的热门图片中构建完备的图片特征库，一旦库建立完成则后续的使用过程中只需要对它不定时更新即可.载密体图片最终被整合为可视化动画（其中的一种呈现形式）然后经过公开的通信链路传递到接收端.接收端经过图片拆分、控制信息提取、算法解析、Turbo解码、解密处理等操作即可获取完整的所要传递的秘密信息.在映射算法模块中本研究提出的IEBVER算法不仅具有安全性高和鲁棒性强的特点，还能在图片的本质信息与需要表达的秘密负载信息之间建立映射关系.该算法以图像信息熵为切入点，对图像进行网格描述、单元熵的提取、熵矩阵的降维、量化等一系列数学操作以便从海量图像大数据中构建隐秘通信所需的完备特征库，下面将重点阐述IEBVER算法的原理和实现.

1.1 IEBVER算法原理

图像的特征有很多，颜色直方图就是一种典型的图像特征，但是颜色直方图存在维数高、缺乏图像空间特征、抗噪声能力差的缺点.而图像信息熵从数学统计的角度对图像的特征进行了定量的描述，它表征图像包含的信息量.本文从图像信息熵的角度出发，将其与需要表达的秘密随机数关联起来，即通过图像的信息熵来表达特定的隨机数，完成零隐写隐秘通信.

信息熵在信息论中的定义为集合X，q（x）中随机变量I（x）的数学期望，其数学表达式如式（1）所示.

其中H（x）表示X的信息熵，q（x）表示X出现的概率.灰度图像中，每个像素可以看成一个自变量m（取值为0～255），整个图像的像素点可以看成集合m，p（m），其中p（m）表示灰度值为m的点出现的概率密度，则根据式（1）信息熵的定义可以得到图像信息熵F的表示如式（2）所示.

F=∑km=0p（m）log （p（m））（2）

其中k表示像素的灰度值（k=255），p（m）表示像素值m在整副图像中出现的概率密度.

式（2）讨论的图像信息熵指的是全局信息熵，其表征了整个图像所有像素点的统计分布，由于没有考虑图像像素点的空间分布的特点这会导致具有相同的概率分布的不同图像具有相同的信息熵.为了合理利用图像的空间信息，本文提出了单元熵的概念.首先引入网格描述符（Grid Description），图2展示了大小为16的网格描述，其将原始图像映射到该网格上可以得到一个n×n的单元方阵.然后求单元熵：即对图2中的每个网格单元用式（2）求全局信息熵，得到如式（3）所示的16×16熵矩阵E.

在得到n×n的熵矩阵之后需要对其进一步降维以减少冗余量和计算量，降维得到的特征值向量为（α1，α2，…，αn），对其量化可以得到二进制比特序列β.

1.2 IEBVER算法实现

IEBVER算法的基本原理对图1中的完备特征库的构建起着关键作用，其实现流程如图3所示.IEBVER算法首先对图片按照大小、格式、内容以及相关度进行筛选.筛选的原则是图片的大小不超过100 kB，图片的格式为JPEG，按文献[9-10]提出的基于分形特征的图片分类算法对图片进行相关度的筛选.该算法[9]由于不需要图片的先验知识，可以将各种风景图片、人工绘制图片、计算机生成的图片等区分开，使得筛选出来的图片都具有高度的相关性，给人以很自然的感觉，从而可以降低监控方的警觉.然后IEBVER算法对筛选后的图片进行如下步骤的操作即可得到其所表达的随机数.

1）将图像映射到大小为16的网格上，用式（2）求单元熵得到熵矩阵；

2）求熵矩阵的特征值，取最大的8个值，得到特征值向量（α1，α2，…，α8）；

3）对特征值向量进行量化得到随机数β，量化公式如式（4）所示；

其中mod（）表示取余操作，round（）表示取整操作，dec2bin（）表示整数转换为向量操作，ai表示特征向量，βi表示一个4比特的行向量.最终得到行向量β=[β1，β2，…，β8].

4）用提取出来的随机数β与特征库中的元素进行遍历比对，若库中还没有能够表达此随机数的图片则将其添加到完备特征库中，若不满足要求则舍弃当前图片然后从图片缓冲库中重新选取一张图片重复以上的操作直到完备特征库建立完毕，库一旦建立完毕则在使用的过程中不需要重新建库只需对它不定时更新即可.

2 Turbo码中QPP交织器的设计

本算法融入了改进的Turbo编码技术来进一步提高系统安全性和鲁棒性.Turbo编码的基本原理是编码器通过交织器把两个分量编码器进行并行级联，两个分量编码器分别输出相应的校验位比特.译码器在两个分量译码器之间迭代译码，参考文献[11]详细阐述了Turbo码编码的原理和性能.交织器是Turbo码的重要组成结构，为了使Turbo码能够较好地适用于本文的系统中，作者对Turbo所使用的QPP（Quadratic Polynomial Permutation）交织器进行了设计，并对其在特定的码率、信噪比下的纠错性能进行了MATLAB仿真分析.

2.1 QPP交织器的基本原理

设F（x）=f0+f1x+…+fmxm为对{0，1，…，N-1}进行置换运算的置换多项式.F（x）的导数F′（x）=f1+2f2x+…+mfmxm-1.对于任意的整数N，F（x）是否为N上的置换多项式可通过文献[11]中的定理判断.所以需要选取合适的N和多项式系数f可以将基于选定的N的置换多项式结构应用于Turbo码交织器中去.本系统中选取m=2，得到的多项式F（x）=f0+f1x+f2x2.而由于二次多项式中常数项f0在交织器中只对移位有影响，对译码性能不起作用，因此将其进一步简化为F（x）=f1x+f2x2.QPP交织器就是利用某些特定的二次多项式，使其满足一定的条件从而成为QPP结构，所以求解多项式的系数f1和f2成为了问题的关键.参考文献[11]给出了系数f1和f2必须满足的基本条件，这里就不再赘述.

2.2 QPP交织器的性能

运用计算机技术可以得到如表1所示的满足该系统的多项式系数f1和f2以及交织器的长度k，Turbo编码器其他结构的工作参数如下：码长为32，64，128，256，512可选，码率为0.8，交织方式为伪随机交织，解码方式为Log-MAP，迭代次数为12次，生产矩阵为（7，5）和（15，17）.

在MATLAB平台下按表1给定的系统工作参数和系数对不同交织长度条件下的Turbo码的误码率性能进行了仿真实验.图4给出了不同信噪比条件下Turbo码的性能随交织长度的变化曲线图.

从图4中可以看出不同信噪比条件下，迭代译码的误比特率随着交织长度的增加而降低.当信噪比为2 dB的時候Turbo码的误比特率性能曲线与交织长度基本呈线性关系，当交织长度大于256的时候误比特率小于10-4，因此，论文设计的QPP交织器的参数合理，能够起到较好的纠错功能，进一步提高了IEBVER算法的鲁棒性.

3 实验与分析

当隐秘通信遭受密切监控时，发送方的异常举

动都会引起监控方的警觉，如果监控方成功获取到原始载体图像则隐秘通信的安全性将遭受严重威胁.同时载密体的鲁棒性也是隐秘通信的一个重要因素，因此本文设计了3个实验和1个分析，分别对IEBVER算法的抗统计分析、抗尺度缩放干扰和抗旋转攻击的能力进行了测试，对IEBVER算法的安全性能做了详细的分析.实验中测试图片是从互联网搜索的大小为256×256的图片，IEBVER算法采用大小为16×16网格描述符.实验中取较大的8个特征值，经过量化后单张图片映射出的随机数长度为32比特.

3.1 实验1

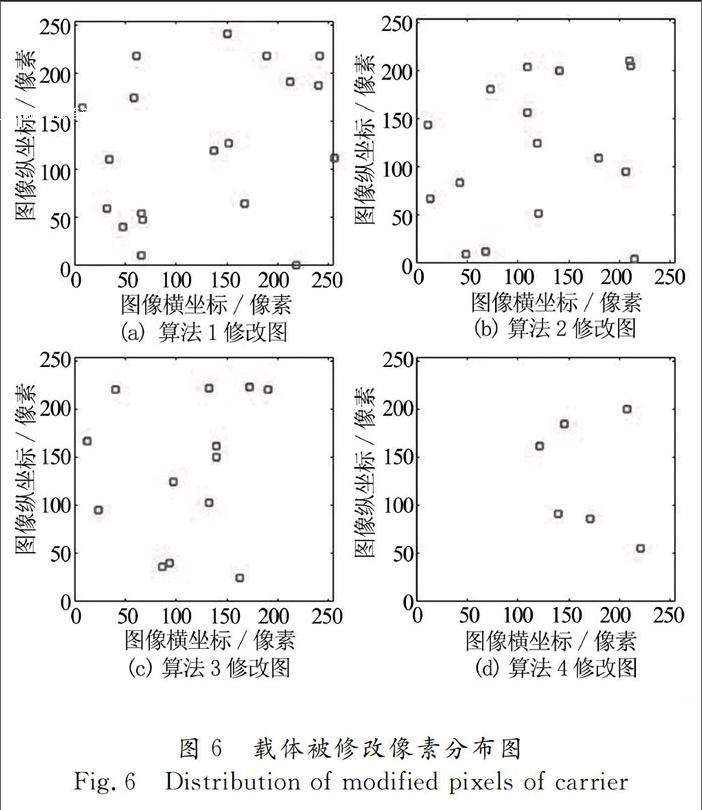
分别采用算法1（LSB[1]）、算法2（改进的LSB[12]）、算法3（矩阵编码[13]）和算法4（STC编码[14]）向单张测试图片的空域嵌入32比特的隐秘信息以测试在监控方获取到原始载体图像的前提下隐秘通信的安全性.图5给出了嵌入负载信息前、后的效果图.

图6是分别采用算法1到4嵌入隐秘信息后原始载密体中被修改的像素点的空间位置分布图，从图中可以看出原始载体图像受到不同程度的修改.算法1直接用隐秘信息比特序列替代最低位平面中载体序列，所以会出现较大程度的修改.算法2在算法1的基础上对嵌入原理做了一定的改进，使得嵌入方式能够更好地抵抗统计分析，原始载体修改的像素点的个数也相应减少.算法3和算法4都采用了编码的方式以保证在负载容量相同的情况下尽量少的修改原始载体像素.算法3基于矩阵编码的方法，利用散列函数在载体序列和负载序列之间构建映射关系.算法4基于STC编码理论，通过维特比译码算法在伴随矩阵中寻找一条失真权重最小的路径.

虽然算法3、4较算法1、2已经大大降低了像素点的修改率，但是当监控方获取到原始载体图像时仍然能够通过比对分析判断载体是否被修改过.所以这种情况下嵌入式的信息隐写算法并不安全.而本文提出的IEBVER算法通过网络热门图像来表达隐秘信息，一方面由于载体图像来源于互联网这样公开的平台，不会引起监控方的警觉，另外一方面由于其本质上没有对原始载体图像做任何的修改，所以即使在严格受控的环境下仍然可以保证隐秘通信内的安全性.

3.2 实验2

实验2对提出的IEBVER算法的抗尺度缩放攻击的能力进行了测试.如图7所示，图7（b）为原始载体图像，分辨率大小256×256；图7（a）为原图经过两倍放大的图像，分辨率变成512×512 ；图7（c）为原图经过两倍缩小的图像，分辨率为128×128 ；图7（d）为原图经过4倍缩小的图像，分辨率为64×64 .

用IEBVER算法从原图和遭受不同程度缩放攻击的被攻击图中进行解映射操作，从而尽可能地恢复出其表达的随机数，设图7（b）恢复出的32比特随机数向量为（b1，b2，…，b32），图7（a）、图7（c）和图7（d）的表示类似.从统计的角度对其误码的个数进行统计，用误码率对其评价.式（5）给出了图7（a）所表示随机数的误码率Ea（加入Turbo纠错编码后的误码率用E′a表示）的求解公式，将ai分别换成ci和di即可求出图7（c）和图7（d）的误码率Ec和Ed.

其中n表示总的比特数，n=32；ai和bi分别表示从图像7（a）和7（b）中解映射得出的随机数向量.对原始载体图像进行1 000次不同尺度的缩放攻击，对1 000次试验的结果取平均，最后的结果如表2所示，E表示各个图未加入Turbo编码的误码率，E′表示加入Turbo后的误码率.

从图7可以看出，经过缩放攻击后原始载体图像的尺寸变得大小不一，但是图像的主要内容没有变，图像的空间位置信息和像素值的统计分布信息没有变，表2进一步证实了该论断.从表2的统计结果来看虽然原始载体图像的尺寸发生了较大的变化，但是解映射恢复的正确率都在95%以上，纠错编码可以进一步提升解映射的正确率.实验结果证明：IEBVER算法具有良好的抗击缩放攻击的能力.

3.3 实验3

实验3对IEBVER算法的抗旋转攻击的特性进行了测试.在图8中，图8（a）为原始载体图像，图8（b）， 图8（c），图8（d）分别为其遭受逆时针旋转90°，180°，270°攻击后的图像.图8（e）为原始载体图像的水平镜像，图8（f），图8（g）和图8（h）分别为图8（e）遭受逆时针旋转（简称：镜逆向）90°，180°和270°攻击后的图像，图8（i）和图8（j）分别是原始载体图像遭受垂直镜像和其水平镜像后的图像（简称：垂-水平镜像）.

分别对不同的载体图像进行1 000组独立测试，按照实验2中的方法对原始载体图像以及不同角度旋转攻击后的图像求逆映射，然后对结果进行统计分析，测试的结果如表3所示.

从表中可以看出原始图像遭受不同程度的旋转攻击后解映射恢复出的数据的误码率控制在8.375%以内，特别是遭受水平镜像及其垂直镜像后误码率为0，即负载信息可以被百分百的恢复.因此，IEBVER算法具有良好的抗击旋转攻击的能力.

3.4 IEBVER算法的安全性能分析

IEBVER算法基于零隐写的思想通过映射的方式而不是嵌入的方法来表达隐秘负载信息本身就达到了“隐身”的目的，对于消除监控方的警觉提高隐秘通信的安全性起到了很好的效果，即使隐匿通信被识破，IEBVER算法的安全性能也足以对抗暴力破解的攻击.

IEBVER采用RSA加密算法，其安全性依赖于大素数因子分解问题，要防范对RSA算法的强行攻击就要选用较大的密钥，然而此时加解密的速度也越来越慢，所以需要在二者之间作一个平衡.目前最好的因式分解算法是平方筛（quadratic sieve）算法和数域筛（number field sieve）算法.相关研究人员就用数域筛算法分解一個664比特的大数需要1023次运算，假设一台计算机每秒可以执行100万次运算，那么要完成664比特的密钥的破解任务也需要100万台的计算机群并行计算4 000年.所以对于日常的使用，768位的密钥已足够，因为当前的因式分解算法和计算机的计算性能已经无法容易地破解它.而本文的随机数具有高安全的特点，结合计算时间开销，所以采用1 024位的密钥长度可以大大提高整个系统的安全性能.

设K1为1 024比特长的RSA非对称加密算法的密钥；K2为6比特长的算法控制密钥，其控制着什么时候选用什么样的随机数表达算法；K3为20比特的量化系数，从图片中提取特征的过程中需要将浮点类型的数加入量化系数后转化为整形数.这3个向量构成了主密钥向量K，如式（6）所示.

通过以上分析可知，K的长度总共有1 050比特的长度，其包含的可能的密钥空间有21 050个组合.假设监控方拥有每秒一万亿次的计算速度，比如中国的银河四系列超级计算机，其也需要约2981年才能暴力破解该系统，所以在当前技术条件下无法采用暴力破解方法来破解该系统.

3.5 IEBVER算法的容量分析

假设单张图片的表达容量为C比特，则构建完整的特征库时所需要的图片数量为2C.即每张图片表达一个C比特的行向量，特征库包含了完整的C比特序列所构成的向量空间.假设负载信息的长度为L比特，则每次发送的图片张数为N=L/C（N向上取整）.假设每张图片的大小为P（MB），则一个完整的特征库所占用的空间为S=P 2C（MB）.在论文的实验过程中C取的是32，P取0.1.实际应用中可根据硬件环境和性能需求折中选取C的值.一般建议取C=16，P=0.1，所以S=65.536（MB），即一个完整的特征库所占用的空间约为65 MB.当特征库构建完成后只需要不定时启动软件更新库即可，保持特征库中的图片都是热门图片并且不重复，在更新的过程中库的大小不会发生大的变化，切合实际应用需求.

4 结 论

在一些秘密级别较高、通信链路监控较严、负载容量较小的隐匿通信场景下，比如安全系统密钥的传递、关键数字、时间、位置等信息的传递，对隐秘通信的要求着重强调高安全性，其容量大小并没有太高的要求.本文提出的IEBVER算法就是一种针对小容量负载的高安全性图像零隐写隐秘通信算法.该算法以图像信息熵为切入点，以网络图像搜索引擎和大数据并行处理方法为技术支撑，从其获取的图像大数据中发掘恰当的图像建立完备的特征库以映射加密后的负载信息，从而进行隐匿通信.一方面由于载体图片是来源于互联网这样的公开平台上的热门图片，所以可以最大程度上削弱监控方的警觉；另外一方面，相对于传统的嵌入式的信息隐写算法，IEBVER算法由于具有零修改的特点所以能够抵抗已知原始载体的统计、比对分析，即使监控方获取到原始载体图像也不会对隐秘通信的安全构成威胁.实验结果表明，该算法对于抗击尺度缩放攻击和旋转攻击也有良好的效果，能够保证在复杂的链路下遭受最严重的攻击后达到95%以上的恢复率.同时，Turbo编码技术和RSA加密算法进一步提高了系统的鲁棒性和安全性.

参考文献

[1] WANG P， MA Q. Information hiding technology based on least significant bit[J]. Information Technology Journal， 2013， 12（20）： 5681-5684.

[2] MUHAMMAD K， AHMAD J， FARMAN H， et al. A secure method for color image steganography using gray-level modification and multi-level encryption[J]. Ksii Transactions on Internet & Information Systems， 2015（9）：1938-1962.

[3] XIE J Q， XIE Q， HUANG D Z. Image information hiding algorithm with high security based on run-length[J]. Computer Science， 2014， 41（3）： 172-175.

[4] SONG J， ZHU Y， SONG J. An information hiding method base on logistic map in DCT domain[J]. Advances in Information Sciences & Service Sciences， 2012， 4（3）： 32-39.

[5] SUN Q， GUAN P， QIU Y， et al. DWT domain information hiding approach using detail sub-band feature adjustment[J]. Telkomnika Indonesian Journal of Electrical Engineering， 2013， 11（7）： 4154-4158.

[6] BILAL M， IMTIAZ S， ABDUL W， et al. Chaos based zero-steganography algorithm[J]. Multimedia Tools and Spplications， 2014， 72（2）： 1073-1092.

[7] ISHIZUKA H， ECHIZEN I， IWAMURA K， et al. Evaluation of a zero-watermarking-type Steganography[C] //Digital-Forensics and Watermarking. Berlin： Springer International Publishing， 2014： 613-624.

[8] 段松青， 吴斌， 于乐，等. PDM： 基于Hadoop的并行数据分析系统[J]. 湖南大学学报： 自然科学版， 2012， 39（10）： 87-92.

DUAN Songqing， WU Bin， YU Le， et al. PDM： A parallel data analysis system based on hadoop[J]. Journal of Hunan University： Natural Sciences， 2012， 39（10）： 87-92. （In Chinese）

[9] LUO Y， LIU T， TAO D， et al. Multiview matrix completion for multilabel image classification[J]. IEEE Transactions on Image Processing， 2015， 24（8）： 2355-2368.

[10]吕昊， 林君， 曾晓献. 改进朴素贝叶斯分类算法的研究与应用[J]. 湖南大学学报： 自然科学版， 2012， 39（12）： 56-61.

LV Hao， LIN Jun， ZENG Xiaoxian. Research and application of improved naive bayesian classification algorithm[J]. Journal of Hunan University： Natural Sciences， 2012， 39（12）： 56-61. （In Chinese）

[11]SCHLEGEL C B， PEREZ L C. Trellis and turbo coding： iterative and graph-based error control coding[M]. New Jersey： John Wiley & Sons， 2015： 205-210.

[12]張红娟， 朱晨鸣. 抗统计分析的新型LSB隐写算法[J]. 计算机工程， 2008， 34（23）： 144-146.

ZHANG Hongjuan， ZHU Chenming. Novel LSB steganography algorithm of against statistical analysis[J]. Computer Cngineering， 2008， 34（23）： 144-146. （In Chinese）

[13]WESTFELD A. F5 -a steganographic algorithm： high capacity despite better steganalysis[J]. Fourth Information Hiding Workshop， 2001， 2137： 289-302.

[14]FARINHA T， FONSECA I， SIMES A， et al. Minimizing embedding impact in steganography using trellis-coded quantization[J]. Proceedings of SPIE - The International Society for Optical Engineering， 2010， 7541（1）： 175-178.