基于路面附着系数估计的AFS控制策略研究
周兵+田晨+宋义彤+吴晓建


摘 要:考虑路面附着条件对车辆横摆响应的影响,设计了路面附着系数修正的主动转向控制策略.为了迅速准确 地获取当前路面附着信息,采用了无迹卡尔曼滤波观测器观测路面附着系数,并用Carsim-Simulink联合仿真验证了此方法的有效性.在传统主动转向控制的基础上将路面附着系数作为输入,设计了滑模控制器.通过Simulink仿真,验证了所设计的滑模控制器在低附着路面、对接路面均能提高车辆的操纵稳定性和理想轨迹跟踪能力.
关键词:主动前轮转向;无迹卡尔曼滤波;路面附着系数;状态观测
中图分类号:U463.4 文献标志码:A
Control Strategy of AFS Based on Estimation of Tire-road Friction Coefficient
ZHOU Bing1,2, TIAN Chen2, SONG Yitong2, WU Xiaojian2
(1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130025, China;
2.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082,China)
Abstract:Considering the impact of tire-road friction coefficient on the yaw motion of vehicles, an active steering control strategy based on the estimation of tire-road friction coefficient was designed. In order to obtain the real-time tire-road friction coefficient, observer was established based on the Unscented Kalman Filter theory, and the co-simulation method with Carsim and Simulink shows that the Unscented Kalman Filter observer is effective. Based on the control of conventional active front steering, a sliding mode controller was designed addressing the tire-road friction coefficient as the input. The simulation analysis by Simulink shows that the sliding mode controller can improve the stability of the vehicle handling and the ideal trajectory tracking ability on slippery and opposite roads.
Key words:active front steering; unscented Kalman filter; friction coefficient; state observation
車辆的横向稳定性是影响车辆高速安全行驶的一项重要性能,前轮转角、路面附着条件等是影响横向动力学稳定性的重要因素;主动前轮转向(AFS)系统能够实现独立于驾驶员的转向干预,达到主动改变前轮转角的目的,使车辆响应尽可能与理想的车辆响应特性一致,从而提高车辆的操纵稳定性.此外,与ESP等现有车辆稳定性控制系统相比,AFS对纵向车速影响较小,能提高车辆的通过速度[1].
学者们对主动转向开展了广泛的研究工作,文献[2]建立了3自由度非线性整车模型,运用μ方法设计主动转向控制器,将建模误差、传感器量测噪声以及路面附着条件的变化作为干扰输入到控制器中,但仅将路面附着变化作为干扰不足以说明路面附着条件变化对车辆横摆运动响应的显著影响.文献[3]建立了8自由度的非线性整车模型,采用滑模控制理论对AFS进行控制,但理想横摆角速度并未考虑路面附着系数的影响,且只验证了高附着路面下的控制效果.车辆在湿滑路面行驶时,轮胎线性区域小,侧向力易发生饱和,若主动转向的控制策略仍和高附着路面相同,则会导致前轮叠加转角过大,轮胎进入非线性区,轮胎侧向力增长小,甚至当超过峰值后会下降,当低于施加控制之前的侧向力值时,不但不能解决不足转向反而会加剧不足转向,给行车安全造成危险.文献[4]考虑了路面附着系数对稳定性因数K的影响从而建立了期望横摆角速度和路面附着系数的关系,但是,在仿真验证中将路面附着系数作为已知量并不符合实际情况.
车辆稳定性控制系统依赖准确实时的车辆状态信号,如横摆角速度、质心侧偏角、路面附着条件等,这对车辆状态信息的获取提出了更高的要求,然而,车辆的某些状态很难直接测量或者测量成本较高,于是本文提出了基于状态估计的软测量.
文献[5]利用无迹卡尔曼滤波(UKF)算法对轮胎纵向力和滑移率进行估计,得到不同路面附着系数下的Slip-slop(ρ-s曲线斜率),建立了几种典型路面附着系数与Slip-slop之间的映射关系.相比基本卡尔曼滤波算法和扩展卡尔曼滤波算法,UKF具有显著优势,可以保证高精度的同时避免求解繁琐的雅克比矩阵,和粒子滤波器相比UKF具有更小的计算量.然而,该方法不能准确、直接地估计出路面附着系数大小,得到的路面附着系数有较大的误差.为了更准确、实时地估计出路面附着系数,本文基于无迹卡尔曼滤波,设计了路面附着系数观测器,并通过Carsim-Simulink联合仿真验证了估计的有效性;同时本文设计了AFS滑模控制器,通过控制量的切换使系统在受到参数摄动和外干扰时具有鲁棒性,并在低附着路面和对接路面验证了其有效性.
1 系统模型
1.1 整车模型
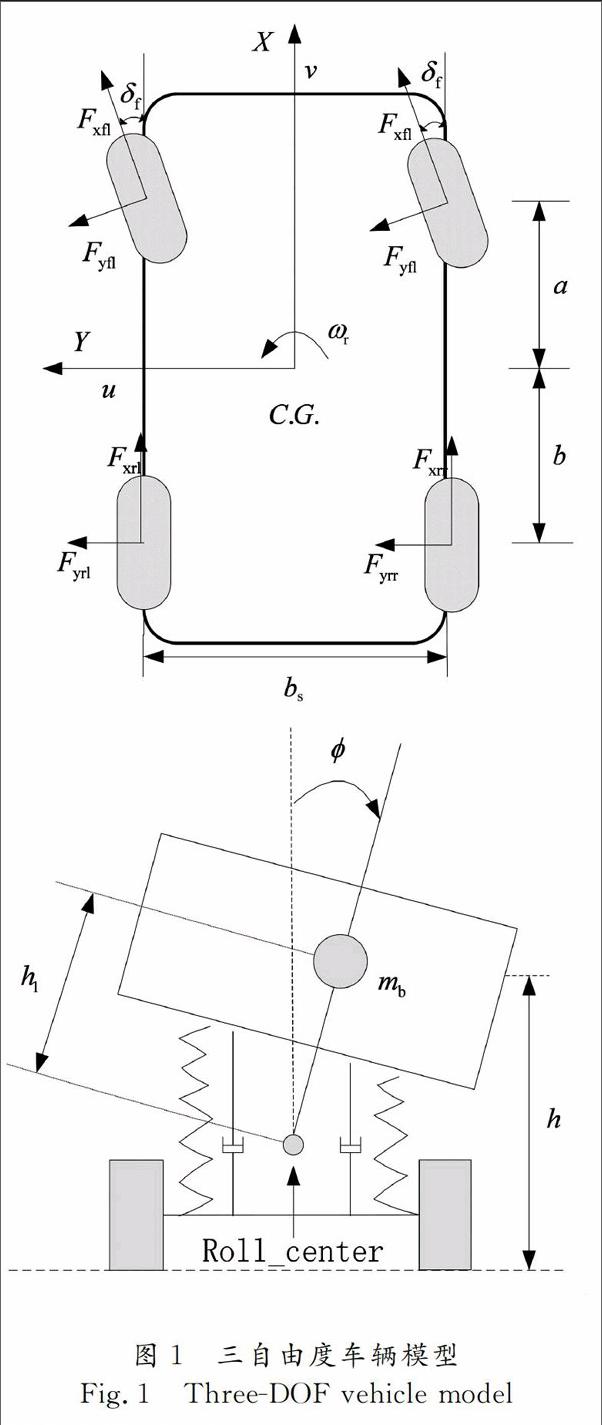
忽略空气阻力侧向风的影响,假设车辆匀速行驶,建立整车横摆、侧向和车身侧倾三自由度模型如图1所示.
整车三自由度动力学方程为[2,6]:
侧向运动
横摆运动
侧倾运动
式中:m为整车质量;mb为簧载质量;v为纵向速度;u为侧向速度;φ为车身侧倾角;ωr为横摆角速度;δf为前轮转角;Fyfl,Fyfr,Fyrl,Fyrr分别为左前轮、右前轮、左后轮、右后轮的侧向力;Bφ为侧倾阻尼;Kφ为侧倾刚度;Ixx为绕x轴的转动惯量;Izz为绕z轴的转动惯量;h1为整车质心至侧倾中心的距离;a为前轴到质心的距离;b为后轴到质心的距离;bs为轮距.
1.2 轮胎模型
轮胎采用基于路面附着系数修正的魔术轮胎模型[7],采用公式(4)计算轮胎侧向力:
式中:By為刚度因子;Cy形状因子;Dy为峰值因子;Ey为曲率因子;α为车轮侧偏角.
2 基于UKF的路面附着系数估计
由图2可以看出不同路面附着系数下,轮胎侧向力极限不同,侧向力极限影响车辆横向动力学响应,因此对车辆行驶的路面附着系数进行在线辨识,对车辆稳定性控制器的设计具有重要意义.对当前路面识别主要有两种方法:一种是基于传感器(光、声、微波、图像等)的路面直接检测方法,另一种是基于车辆动力学参数的估计方法.前者虽然能够获得较好的识别效果,但是识别系统结构复杂,成本高[8].
基于状态估计的软测量方法是将参数的软测量问题转化为状态观测和状态估计.卡尔曼滤波是一种典型的状态估计方法,车辆是一个非线性系统,在对其状态或者参数进行估计时需要非线性观测器.经典卡尔曼滤波和扩展卡尔曼滤波用于非线性系统估计都有各自的不足,无迹卡尔曼滤波是近几年兴起的一种新的非线性估计方法,具有良好的准确性和实时性,被广泛应用于各个领域.因此本文利用三自由度非线性整车模型建立无迹卡尔曼滤波观测器来估计路面附着系数.
采用二阶高斯马尔可夫过程将路面附着系数描述成待估计量[9]:
式中,分别是路面附着系数的一阶导数和二阶导数;ωμ为零均值的白噪声.将待估计参数增补到车辆非线性状态方程中,得到本文所采用的估计模型:
系统的测量方程为:
式中x(t)=β,ωr,μ,T为状态变量;y(t)=ωr,ayT为测量输出;u(t)=δf,δf为控制变量.w(t)和v(t)分别为系统噪声和测量噪声,假设两者为零均值的白噪声,且互不相关.
无迹变换(UT变换)是无迹卡尔曼滤波算法的核心和基础,UT变换的思想是:在确保采样均值和协方差Px的前提下,选择一组Sigma点集,将非线性变换应用于采样的每个Sigma点,得到非线性转换后的点集和Py是变换后Sigma点集的统计量[10].
使用UKF算法时,需要对初值进行设定.本文根据文献[5]提出的初值选择方法对状态变量、误差方差阵P、系统噪声方差阵Q以及测量噪声方差阵R进行赋初值.
UKF算法流程如图3所示.
Carsim作为成熟的商业软件具有自由度高、仿真精度高、运行稳定等显著特点.本文利用Carsim-Simulink联合仿真来验证UKF估计路面附着系数的有效性.在Carsim中选择B-class,前轮驱动模型,修改相应车辆参数进行仿真,仿真框图如图4所示.
仿真工况设置如下:汽车以60 km/h的速度在低附着路面(μ=0.3)和对接路面(路面附着系数从0.85突变为0.5)行驶,在1~1.5 s进行90°斜坡阶跃转向,仿真结果图5所示.可以看出在不同路面附着条件下,无迹卡尔曼滤波均可对路面附着系数进行实时估计,估计误差在可接受范围之内.
3 主动转向控制策略
本文采用如图6所示的主动转向控制策略,将方向盘转角信号和易由传感器测得的量提供给车辆状态观测器,从而获得车辆稳定性重要量的观测值,将其与由参考模型得到的理想参考值一起输入到控制系统.通过两者之差产生控制量控制AFS转角电机,转角电机产生的叠加转角与驾驶员施加的方向盘转角相叠加作为车辆转向轮的总转角输入,使得车辆稳定性重要量趋近于理想参考值.
3.1 理想参考模型
车辆行驶过程中,驾驶员施加转向输入后横摆角速度和质心侧偏角等响应能够同转向输入符合线性关系,这种线性关系能给驾驶员更直接的驾驶感受,有利于安全操控车辆.线性二自由度车辆模型状态空间方程如下:
式中:x=β,ωdT为车辆状态变量;k1和k2分别为前后轮胎侧偏刚度.
令=,dT=0可得理想横摆角速度
式中:K=ma+b2ak2-bk1为车辆稳定性因数.
但是这样获得的期望值并不安全,因为轮胎侧向力极限和路面附着系数有关,所以理想横摆角速度存在上限值[11].
式中:μ为路面附着系数.
3.2 滑模控制器设计
人车路系统是一个复杂的时变、不确定、高度非线性系统,很难建立一个准确的数学模型,这就使许多基于模型的控制方法的稳定性大打折扣.本文选择滑模控制来设计控制器,滑模控制具有响应快速、对参数变化及扰动不灵敏、物理实现简单的特点.
选取控制误差为实际横摆角速度和理想横摆角速度之差:
式中:ωr为车辆实际测得的横摆角速度;ωd为理想横摆角速度.选择切换函数为
4 仿真分析
在MATLAB/Simulink中建立整车模型,运用论文设计的路面附着系数估计方法和主动转向控制策略进行仿真分析,并将滑模控制和PID控制进行对比.
仿真工况1:设置前轴轮胎的路面附着系数μf=0.8,后轴轮胎的路面附着系数μr=0.4,以构建一个等效的过多转向工况,以60 km/h在低附着路面(μ=0.3)上行驶,1~2 s给转向盘施加90°斜坡阶跃转角输入.
仿真结果如图7所示,可以看出车辆在低附着路面上行驶时,有AFS控制的车辆横摆角速度响应能始终跟踪理想模型,质心侧偏角始终保持在较小值.无AFS控制的车辆,横摆角速度呈发散状,说明车辆处于失稳状态.未引入UKF估计μ的理想参考值在低附着路面上处于过度转向状态,显然不能将其作为参考值进行AFS控制,否则极易使车辆在低附着路面上失稳,造成安全隐患.
仿真工况2:设置车速为60 km/h,1~2 s转向盘施加90°斜坡阶跃转角.设置前轮路面附着系数在仿真开始5~5.5 s时由0.85渐变为0.5,后轮路面附着系数时间延迟t=L/vx,同样由0.85渐变为0.5,模拟车辆从干沥青路面行驶到到湿沥青路面上路面附着系数变化对操作稳定性的影响.
仿真结果如图8所示,从中可以看出有AFS控制的车辆横摆角速度响应能始终跟踪理想模型,质心侧偏角始终保持在较小值.无AFS控制的车辆,横摆角速度收敛速度慢、质心侧偏角变化大.未考虑路面附着系数的理想参考值在对接路面上已经产生了过度转向,容易使驾驶员紧张,产生误操作,影响行驶安全性.
从图7和图8可以看出,滑模控制在响应速度和控制精度上均优于传统的PID控制,且改变仿真工况时,PID参数需要重新整定,滑模控制的鲁棒性也优于PID控制.
5 结 论
本文设计了一种考虑路面附着系数影响的主动转向控制策略.首先基于魔术轮胎模型建立了整车数学模型;然后设计了基于无迹卡尔曼滤波的路面附着系数观测器,并通过Carsim-Simulink联合仿真验证了估计的有效性;接着设计了滑模控制器,考虑路面附着系数对理想参考值最大值的限制;最后,在MATLAB/simulink中建立了仿真模型,在不同工况下进行仿真,结果表明,主动转向控制策略应考虑路面附着系数的影响,在不同的路面附着条件下,滑模控制器均能达到很好的控制效果,提高了车辆的行驶安全性和稳定性.
参考文献
[1] 李强,施国标,林逸,等. 主动前轮转向控制技术研究现状与展望[J]. 汽车工程,2009,31(7):629-633.
LI Qiang,SHI Guobiao, LIN Yi,et al. Status quo and prospect of the research on active front steering control technology[J].Automotive Engineering,2009,31(7):629-633.(In Chinese)
[2] CHAO-CHUN Y, LONG C,SHAO-HUA W, et al. Robust active front steering control based on the mu control theory[C]//Electrical and Control Engineering (ICECE).Wuhan,2010: 1827-1829.
[3] MOUSAVINEJAD I, KAZEMI R, KHAKNEJAD M B. Nonlinear controller design for active front steering system[C]//International Conterence on Mechanical,Industrial and Manufacturing Engineering.Cape Town, South Afica,2012:6-11.
[4] SONG J. Design and evaluation of active front wheel steering system model and controller[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2014, 7(1): 367-374.
[5] 林棻,黄超. 采用UKF算法估计路面附着系数[J]. 哈尔滨工业大学学报,2013,45(7):115-120.
LIN Fen, HUANG Chao.Unscented Kalman filter for road friction coefficient estimation[J]. Journal of Harbin Institute of Technology, 2013,45(7):115-120. (In Chinese)
[6] 袁希文,文桂林,周兵. 基于控制分配的主動前轮独立转向车辆转角分配算法[J]. 中国机械工程,2015,26((9):1243-1250.
YUAN Xiwen WEN Guilin,ZHOU Bing. Road wheel angle distribution algorithm for road vehicles with AIFS based on control allocation[J].China Mechanical Engineering,2015,26(9):1243-1250. (In Chinese)
[7] 周兵,徐蒙,范璐. 低附着路面电动助力转向控制策略[J]. 湖南大学学报:自然科学版,2015,42(2):29-34.
ZHOU Bing, XU Meng,FAN Lu. Control strategy for electric power steering on low friction coefficient roads [J] Journal of Hunan University:Natural Sciences,2015,42(2):29-34. (In Chinese)
[8] 杨福广,李贻斌,阮久宏,等. 基于扩张状态观测器的路面附着系数实时估计[J]. 农业机械学报,2010,41(8):6-9,15.
YANG Fuguang, LI Yibin,YUAN Jiuhong,et al. Real-time estimation of tire road friction coefficient based on extend state observer[J].Transactions of the Chinese Society for Agricultural Machinery,2010,41(8):6-9,15. (In Chinese)
[9] RAJAMANI R, PIYABONGKARN N, LEW J, et al. Tire-road friction-coefficient estimation[J]. IEEE Control Systems, 2010, 30(4): 54-69.
[10]SIMON D. Optimal state estimation Kalman H lafinity and nonlinear approaches[M]. Hoboken, NJ:Wiley-Interscience,2006:121-135.
[11]RAJAMANI R. Vehicle dynamics and control[M]. Boston, MA:Springer US, 2006:45-52.
[12]刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2012:25-31.
LIU Jinkun, Sliding mode control design and MATALB simulation[M].Beijing:Tsinghua University Press,2012:25-31. (In Chinese)

