时间尺度上Nabla变分问题的非完整力学系统的Noether理论*
祖启航,朱建青
(苏州科技大学数理学院,江苏 苏州 215009)
时间尺度上Nabla变分问题的非完整力学系统的Noether理论*
祖启航,朱建青
(苏州科技大学数理学院,江苏 苏州 215009)
研究了时间尺度上Nabla变分问题的非完整力学系统的Noether理论。根据时间尺度上的微积分理论和Delta导数与Nabla导数之间关系,建立了时间尺度上Nabla导数的非完整Lagrange方程。根据时间尺度上Nabla变分问题的Hamilton作用量在无限小变换下的变换性质,建立了Nabla变分问题的非完整力学系统的Noether等式,并找到了相应的守恒量。最后,举例说明结果的应用。
时间尺度;Nabla变分;非完整系统;Noether等式;守恒量
1988年德国学者Hilger[1]在他的博士论文中提出时间尺度的微积分理论,其主要目的是把连续和离散进行统一[2-3]。然而时间尺度上的微积分定理并不是唯一的,一般有两种方法:一种是针对前跳算子定义的Delta微积分理论,另一种是针对后跳算子定义的Nabla微积分理论[4]。对Delta变分问题的研究已经取得了许多成果[5-10]。事实上在求解最优化控制、经济学模型等领域利用Nabla微积分求解更为方便[11]。2001年,Atici和Guseinov[4]给出了Nabla微积分理论。随后,Martins和Torres[12]进一步研究了Nabla微积分理论,并将理论推广到高阶系统。Caputo[13]定义了对偶时间尺度,研究了Delta导数和Nabla导数之间的变换关系,进一步给出了Nabla导数的Euler-Lagrange函数。为了研究不同算子在对应不同导数情况下的关系,Bourdin[14]对前跳算子在Nabla导数情况下进行了探讨,建立了求导法则,并进一步给出了混合导数的Euler-Lagrange函数。
对称性与守恒量是分析力学研究的一个重要方面。尽管在约束力学系统的对称性与守恒量方面的研究已经取得了一系列重要成果[15-26]。但对于时间尺度上Nabla变分问题的对称性与守恒量的研究还很少。Martins和Torres利用Delta微积分和Nabla微积分理论之间关系,通过Delta变分问题的完整力学系统的Noether定理[22],给出了Nabla导数的完整力学系统的对称性,并找到相应的守恒量[27]。本文基于时间尺度的微积分理论,以及Delta导数和Nabla导数之间的交换关系,根据时间尺度上Delta变分问题的非完整Lagrange方程,建立了时间尺度上Nabla变分问题的非完整Lagrange方程,结合时间尺度上Delta变分问题的Lagrange系统的Noether相关定理,建立了时间尺度上Nabla变分问题的非完整力学系统的Noether等式,并找到相应的Noether守恒量。文末,举例说明相关结论的应用。
1 时间尺度上的微积分理论
时间尺度上Delta (Δ)微积分理论详见文献[9]。文章重点介绍Nabla(▽)微积分理论。


后跳算子ρ为

定义2 若σ(t)>t,则称t为右离散;若σ(t)=t,则称t为右稠密;若ρ(t) 引理1 如果函数f在点t处是Δ可微的,那么fσ(t)=f(t)+μ(t)fΔ(t)。 引理2 如果函数f在点t处是▽可微的,那么fρ(t)=f(t)-ν(t)f▽(t)。 ([a,b])*=[-b,a], 函数f是右稠连续(左稠连续)当且仅当对偶函数f*是左稠连续(右稠连续); (f▽)*(-t)=-(f* 如果函数f:[a,b]→是右稠连续,则;如果函数f:[a,b]→是左稠连续,则▽ 一般情况下,对于函数的Δ和▽导数具有相同的表达形式,如和函数、积函数等,具体证明过程见文献[12]。Δ导数与等时变分之间的交换关系[23], δqΔ=(δq)Δ,δqσ=(δq)σ 同样易得▽导数与等时变分交换关系: δq▽=(δq)▽,δqρ=(δq)ρ 上式可称为▽导数与非等时变分间的交换关系。 首先考虑由Bohner定义的时间尺度上的基本变分问题[5] hs(a)=A,hs(b)=B(s=1,…,n) (1) 再考虑▽导数形式的基本变分问题 ▽t→min, qs(c)=C,qs(d)=D(s=1,…,n) (2) 假设时间尺度上动力学系统的运动受g个双面理想Chetaev型非完整约束 (s=1,…,n;β=1,…,g) (3) (4) 式中∂if表示函数f关于第i个变量的偏导数。则称(4)式为带有▽导数的Chetaev条件。 在基本变分问题(1)下,已知时间尺度上Delta变分问题的非完整力学系统的微分方程为[23] (s,k=1,…,n) (5) 根据引理3和定义8可得如下引理。 假设qs是基本变分问题(2)的局部最小值,则根据引理4有 η(-c)=C,η(-d)=D (6) (7) 根据对偶时间尺度的等式关系 ∂3L*(t,w,v)=-∂3L(-t,w,-v), ∂2L*(t,w,v)=∂2L(-t,w,-v) (8) 易得 (9) 根据引理3的基本公式,可得 (10) (11) (s,k=1,…,n;β=1,…,g) (12) 其中 (13) 则称方程(12)与时间尺度上非完整系统(3),(11)相应的时间尺度上完整系统的运动方程。 ▽t (14) 引入时间和广义坐标的无线小变换 (15) 这里ε为无限小参数,τ,ξs为无限小变换的生成函数。τ:[ta,tb]×n,ξs:[ta,tb]×n是▽可微函数。假设对任意qs∈V和ε,映射t∈[ta,tb]α(t):=T(t,qs,ε)∈是左稠连续的函数,而且它是在新的时间尺度上带有后跳算子和导数的一个象。 ▽t= (16) τ (17) 其中 τρ(t,qk(t)) =τ(ρ(t),qk(ρ(t))), τ 证明 根据引理4,▽导数形式的作用量方程(14)为 I*[ys(·)]= (18) (19) (20) (21) 利用Δ和▽导数之间的关系,有如下等式 (22) 利用(9)式,并将(22)式代入(21)式中,得 (23) (24) 则证得定理1。(17)可称为时间尺度上Nabla变分问题的非完整力学系统的Noether等式。 定理2 如果泛函I是定义10下的广义准对称不变量,那么有守恒量 (25) (26) 由(9)和(22)式,上式可进一步得 (27) 令x∈[ta,tb]k⊆[a,b]k,x=-t,则上式为 (28) 得到守恒量(25)。定理证得。 (25)式可称为时间尺度上Nabla变分问题的非完整力学系统的守恒量。 由以上定理可得如下推论 (29) 根据定理2,可得经典的非完整非保守系统的守恒量[29] (30) 定义时间尺度 已知二自由度系统的Lagrange函数为 (31) 所受的非完整约束为 (32) 由运动微分方程(11)给出 (33) 由(32)和(33)可得 (34) 由(32)式、(33)和(34)式求得 (35) 根据(17)式和(4)式,可得 (36) (37) 对(36)式和(37)式进行求解 (38) 所以根据定理2,可得到守恒量 (39) 时间尺度将离散和连续进行了统一,其微积分有多种表达形式,如Δ型、▽型、α型[6]以及◇混合型等[30],本文主要研究前两个。虽然Δ导数与▽导数,在形式上有诸多相似之处,但在实际计算中两者又有不同。本文根据对偶时间尺度,利用二者之间的等式关系,建立了▽导数的非完整力学系统的Lagrange微分方程。根据时间尺度上无限小变换下的广义准对称不变量,得到了时间尺度上Nabla变分问题的非完整力学系统的Noether等式和守恒量,并讨论了在取特殊条件时,得到相应的经典力学中Noether定理。文章是对时间尺度上Nabla变分问题在分析力学中的应用进行了研究,可进一步拓展到其它力学系统。本文只是研究了▽导数力学系统的Noether理论,从形式上也是一种特殊情况,文章可进一步研究更为一般情况的表达形式,如◇混合型等力学系统的Noether理论。 致谢:对张毅教授的悉心指导深表感谢! [1]HILGERS.Einmaβkettenkalkulmitanwendungaufzentrumsmannigfaltigkeiten[D].Wurzburg:UniversitätWurzburg, 1988. [2]HILGERS.Analysisonmeasurechains-aunifiedapproachtocontinuousanddiscretecalculus[J].ResultsMath, 1990, 18(1/2):18-56. [3]HILGERS.Differentialanddifferencecalculus-unified[J].NonlinearAnal, 1997, 30(5):2683-2694. [4]ATICIFM,GUSEINOVGS.OnGreen'sfunctionsandpositivesolutionsforboundaryvalueproblemsontimescales[J].JComputApplMath, 2002, 141(1/2):75-99. [5]BOHNERM.Calculcusofvariationsontimescales[J].DynamSystemsAppl, 2004, 13(12): 339-349. [6]AHLBRANDTCD,BOHNERM,RIDENHOURJ.Hamiltoniansystemsontimescales[J].JMathAnalAppl, 2000, 250(2):561-578. [7]AGUILARRC,RETEGUILA,POSTEL-VINAYMC.Higher-ordercalculusofvariationsontimescales[J].SpringerBerlinHeidelberg, 2008, 136(1):149-159. [8]ZHANZD,WEIW,XUHL.Hamilton-Jacobi-Bellmanequationsontimescales[J].MathComputModel, 2009, 49(9/10):2019-2028. [9]BOHNERM,PETERSONA.Dynamicequationontimescales-Anintroductionwithapplications[M].BostonBaselBerlin:Birkhäuser, 2001. [10]BOHNERM,PETERSONA.Advancesindynamicequationontimescales[M].BostonBaselBerlin:Birkhäuser, 2003. [11]ATICIFM,BILESDC,LEBEDINSKYA.Anapplicationoftimescalestoeconomics[J].MathComputModel, 2006, 43(7/8):718-726. [12]MARTINSN,TORRESDFM.CalculusofvariationsontimescaleswithNabladerivatives[J].NonlinearAnal, 2008, 71(12):e763-e773. [13]CAPUTOMC.TimeScales:fromNablacalculustoDeltacalculusandviceversaviaduality[J].IntJDifferenceEqu, 2010, 5(1):25-40. [14]BOURDINL.Nonshiftedcalculusofvariationsontimescaleswith▽-differentiableσ[J].JMathAnalAppl, 2014, 411(2): 543-554. [15] 梅凤翔. 李群和李代数对约束力学系统的应用[M]. 北京:科学出版社,1999.MEIFX.ApplicationsofLiegroupsandLiealgebrastoconstrainedmechanicalsystems[M].Beijing:SciencePress, 1999. [16]CHENXW,LIYM,ZHAOYH.Liesymmetries,perturbationtosymmetriesandadiabaticinvariantsofLagrangesystem[J].PhysicsLettersA, 2005,337(4/5/6):274-278. [17] 张毅. 相空间中类分数阶变分问题的Noether对称性与守恒量[J]. 中山大学学报(自然科学版),2013, 52(4):45-50.ZHANGY.Noethersymmetryandconservedquantityforafractionalaction-likevariationalprobleminphasespace[J].ActaScientiraumNaturaliumUniversitatisSunyatseni, 2013, 52(4):45-50. [18]LUOSK,LIZJ,PENGW,etal.ALiesymmetricalbasicintegralvariablerelationandanewconservationlawforgeneralizedHamiltoniansystems[J].ActaMechanica, 2013, 224(1):71-84. [19] 金世欣, 张毅. 相空间含时滞的非保守力学系统的Noether定理[J]. 中山大学学报(自然科学版),2014, 53(4):56-61.JINSX,ZHANGY.Noethertheoremfornonconservativemechanicalsystemwithtimedelayinphasespace[J].ActaScientiraumNaturaliumUniversitatisSunyatseni, 2014, 53(4):56-61. [20]ZHAIXH,ZHANGY.NoethersymmetriesandconservedquantitiesforBirkhoffiansystemswithtimedelay[J].NonlinearDynamics, 2014, 77(1/2):73-86. [21] 何胜鑫, 朱建青, 张毅. 基于分数阶模型的非保守系统的Noether准对称性[J]. 中山大学学报(自然科学版),2016, 55(2):58-63.HESX,ZHUJQ,ZHANGY.Noetherquasi-symmetryfornon-conservativesystemsbasedonfractionalmodel[J].ActaScientiraumNaturaliumUniversitatisSunyatseni, 2016, 55(2):58-63. [22]BARTOSIEWICZZ,TORRESDFM.Noether,theoremontimescales[J].JMathAnalAppl, 2008, 342(2): 1220-1226. [23]CAIPP,FUJL,GUOYX.Noethersymmetriesofthenonconservativeandnonholonomicsystemontimescales[J].SciChina:PhysMechAstron, 2013, 56(5):1017-1028. [24]SONGCJ,ZHANGY.NoethertheoremforBirkhoffiansystemsontimescales[J].JMathPhys, 2015, 56: 102701. [25] 张毅. 时间尺度上Hamilton系统的Noether理论[J]. 力学季刊, 2016, 37(2):214-224.ZHANGY.NoethertheoryforHamiltoniansystemontimescales[J].ChineseQuarterlyofMechanics, 2016, 37(2):214-224. [26]ZUQH,ZHUJQ.Noethertheoremfornonholonomicnonconservativemechanicalsystemsinphasespaceontimescales[J].JMathPhys, 2016, 57:082701. [27]MARTINSN,TORRESDFM.Noether’ssymmetrytheoremforNablaproblemsofthecalculusofvariations[J].AppMathLett, 2010, 23(12):1432-1438. [29] 刘端. 非完整非保守动力学系统的守恒律[J]. 力学学报, 1989, 21(1):75-83.LIUD.Conservationlawsofnonholonomicnonconservativedynamicalsystems[J].ActaMechanicaSinica, 1989, 21(1):75-83. [30]SHENGQ,FADAGM,HENDERSONJ.Anexplorationofcombineddynamicderivativesontimescalesandtheirapplications[J].NonlinearAnaRealWorldAppl, 2006, 7(3):395-413. Noether theorem for nonholonomic mechanical systems of Nabla variational problem on time scales ZUQihang,ZHUJianqing (College of Mathematics and Physics, Suzhou University of Science and Technology, Suzhou 215009, China) The Noether theorem for nonholonomic mechanical systems of Nabla variational problem on time scales is studied. Firstly, based on the relationship between the Delta calculus and the Nabla calculus on time scales and the theory of time scale, the nonholonomic Lagrange equation for Nabla variational problem on time scales is established. Secondly, according to invariance of the Hamilton action under the infinitesimal transformation of Nabla variational problem on time scales, the Noether identity for nonholonomic mechanical systems is established, and the corresponding Noether conserved quantity is obtained. Finally, an example is presented to illustrate the application of the results. time scales; Nabla variation; nonholonomic systems; Noether identity;conserved quantity 2016-04-10 基金项目:国家自然科学基金(11572212);苏州科技大学研究生科研创新计划(SKCX15_061) 祖启航(1991年生),男,研究方向:力学中的数学方法;E-mail:zqhusts@163.con 朱建青(1962年生),男, 研究方向:应用数学;E-mail:zjq@mail.usts.edu.cn 10.13471/j.cnki.acta.snus.2017.01.010 O A 0529-6579(2017)01-0058-08











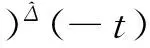
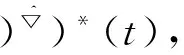


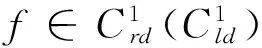
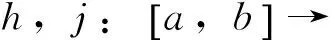
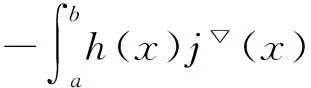
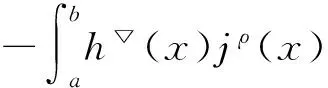
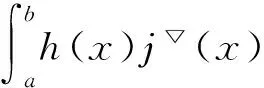
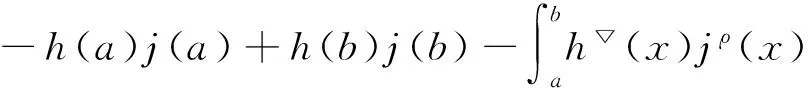
2 时间尺度上Nabla变分问题的非完整力学系统的微分方程


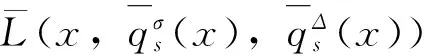


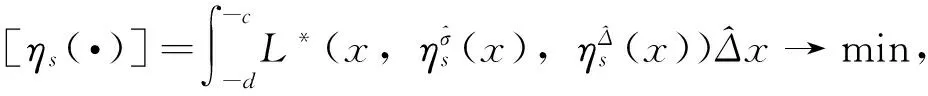
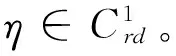
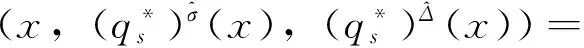
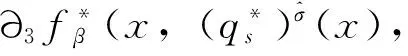


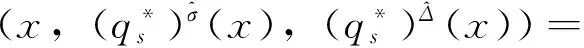
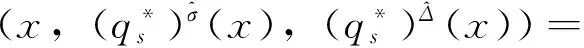
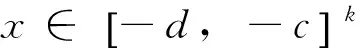
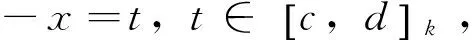

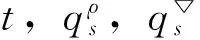
3 时间尺度上Nabla变分问题的非完整力学系统的Noether定理


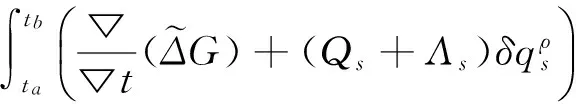
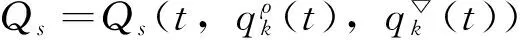

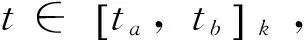

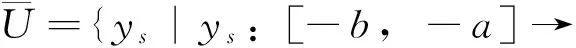
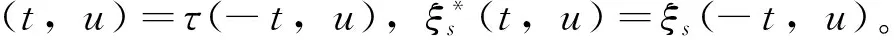

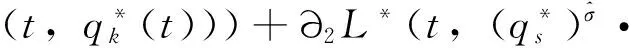
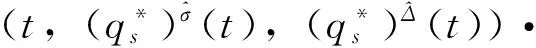
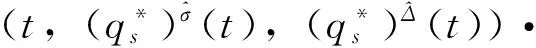

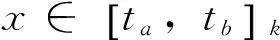
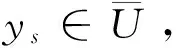
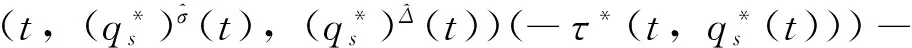
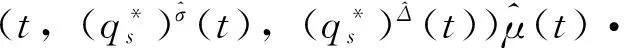

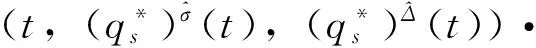


4 算 例

5 结 论


