柯西不等式在求多元函数最值中的应用再探
2017-05-17 09:56:02江西省赣州市第三中学341000温芳勇
数理化解题研究 2017年10期
江西省赣州市第三中学(341000) 温芳勇●
柯西不等式在求多元函数最值中的应用再探
江西省赣州市第三中学(341000)
温芳勇●
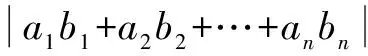
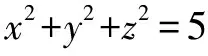
解 观察变元x、y、z的次数,依低次在不等式左边、较高次在不等式右边的原则,确定要凑配成(x+2y+3z)2≤(x2+y2+z2)( )这种形式.
故括号里面的数很明显是12+22+32.
据此有,(x+2y+3z)2≤ 5×(12+22+32)=70,
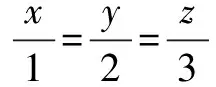
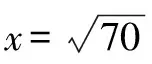
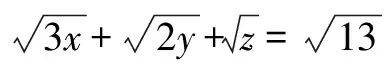
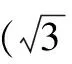
例3 设x+y+z=1,求函数u=2x2+3y2+z2的最小值.
解 要凑配成柯西不等式,观察其变元的次数,低次在左边、高次在右边的原则得不等式的形式是:(x+y+z)2≤( )(2x2+3y2+z2).
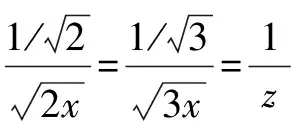
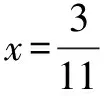
通过上述三个例子,我们可以发现利用柯西不等式解题的一个关键是如何由已知条件凑配到柯西不等式.在这里,我们发现柯西不等式形式的一个规律是含低次方变元的代数式在不等号的左边,含更高次方变元的代数式在不等式右边,以此为突破口来进行构建柯西不等式就显得容易多了.
[1] 傅建红.例说根式型柯西不等式在求多元函数最值中的应用[J].中学数学研究,2012(3).
G632
B
1008-0333(2017)10-0034-01
猜你喜欢
高师理科学刊(2020年2期)2020-11-26 06:01:26
语数外学习·高中版中旬(2020年2期)2020-09-10 07:22:44
河北理科教学研究(2020年1期)2020-07-24 08:14:34
数学物理学报(2019年2期)2019-05-10 11:32:50
数理化解题研究(2017年4期)2017-05-04 04:07:54
潍坊学院学报(2016年2期)2016-12-01 12:59:51
Coco薇(2016年7期)2016-06-28 02:09:09
潍坊学院学报(2015年2期)2015-12-31 09:09:36
作文·初中版(2015年10期)2015-10-26 16:37:53
泰山学院学报(2015年6期)2015-06-07 11:09:41

