中高层生态复合墙体正截面压弯承载力分析
张程华,邱继生,侯丕吉,张 敏,黄 炜
(1.西安科技大学 建筑与土木工程学院, 陕西 西安 710054;2.西安建筑科技大学 土木工程学院, 陕西 西安 710055)
中高层生态复合墙体正截面压弯承载力分析
张程华1,邱继生1,侯丕吉1,张 敏2,黄 炜2
(1.西安科技大学 建筑与土木工程学院, 陕西 西安 710054;2.西安建筑科技大学 土木工程学院, 陕西 西安 710055)
为了提高墙体的水平承载力和改善其抗震性能,将传统生态复合墙结构与混凝土竖向约束构件有机结合提出中高层生态复合墙混合结构体系。根据中高层生态复合墙体实际压弯状态下的受力特性及墙体的特殊构造形式,提出墙体合理的简化计算模型;基于平截面假定,结合材料本构模型及几何关系,建立中高层生态复合墙体正截面压弯承载力计算的等效矩形应力图形,推导墙体正截面压弯承载力实用计算公式,并对前期试验墙体进行极限承载力分析。理论和试验表明:该公式概念明确、计算简单,可用于指导中高层生态复合墙体混凝土竖向约束构件的配筋。
中高层生态复合墙体;正截面压弯承载力;界限受压区高度;大偏压破坏;小偏压破坏
随着国家“十二五”规划的实施与推进,社会城镇化进程的步伐进一步加快,城镇规模不断扩大,用地紧张、基础设施滞后、环境污染等城镇化问题集中涌现。为解决上述问题,城镇土地的利用必须朝着综合化、集约化的方向发展。居住建筑在城镇中量大面广,提高居住建筑的密度和容积率可有效地节约土地资源、提高城镇的运行效率,住宅层数的提高已不可避免。然而,过分追求建筑层数及城镇的聚集效应,势必导致容积率和建筑密度过高;同时,超高层建筑建设投资大,管理费用高,罕遇灾害下损失严重,不可能大规模建造[1-3]。故8~18层左右的中高层建筑才是我国城镇住宅建筑发展的主要方向。这就对传统生态复合墙结构体系[4-8]向中高层发展提出新的要求。然而,在中高层建筑应用时,随着建筑高度的增加,水平荷载成为结构设计的主要控制因素,结构容易承受较大整体弯矩作用。传统生态复合墙结构体系在中高层的应用明显受到连接柱抗力较弱、预制生态复合墙板竖向连接不连续、结构抗侧力能力不足等方面的制约。
基于以上研究现状及前期研究成果,将传统生态复合墙结构与混凝土竖向约束构件有机结合,相互取长补短各汲优点,提出中高层生态复合墙混合结构体系。它主要由预制生态复合墙板、混凝土竖向约束构件、暗梁及楼板装配现浇而成(见图1)。其中网格墙板耗能减震、生态节能、经济实用;竖向约束构件可根据建筑物高度、抗震设防烈度、场地类型及建筑功能等因素优化设计其截面肢厚比、截面形式及截面配筋率,其布置灵活,避免室内柱楞凸出,作为结构的主要竖向连续受力构件与网格墙板共同工作,形成联合抗侧力结构体系,从而使中高层生态复合墙混合结构体系的抗震性能显著提高。
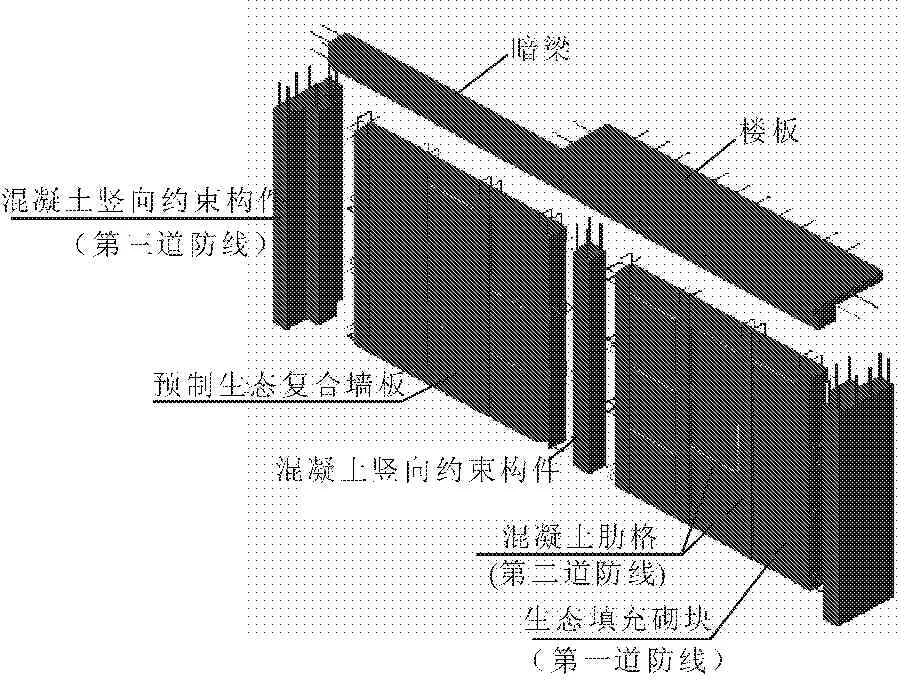
图1 中高层生态复合墙混合结构体系构造示意图
为研究中高层生态复合墙体压弯性能,本文根据墙体实际压弯状态下的受力特性及其的特殊构造形式,提出墙体合理的简化计算模型。基于平截面假定,结合材料本构模型及几何关系,建立中高层生态复合墙体正截面压弯承载力计算的等效矩形应力图形,并推导出墙体正截面压弯承载力实用计算公式。
1 试验简介
1.1 试验简介
本试验考虑到试验条件及加载设备限制,缩尺比例取为1/2,取底部两层模拟12层墙体。共选试件2块,试验加载为单调[8]加载,加载装置如图2所示。试件各参数详见表1[9-10]。
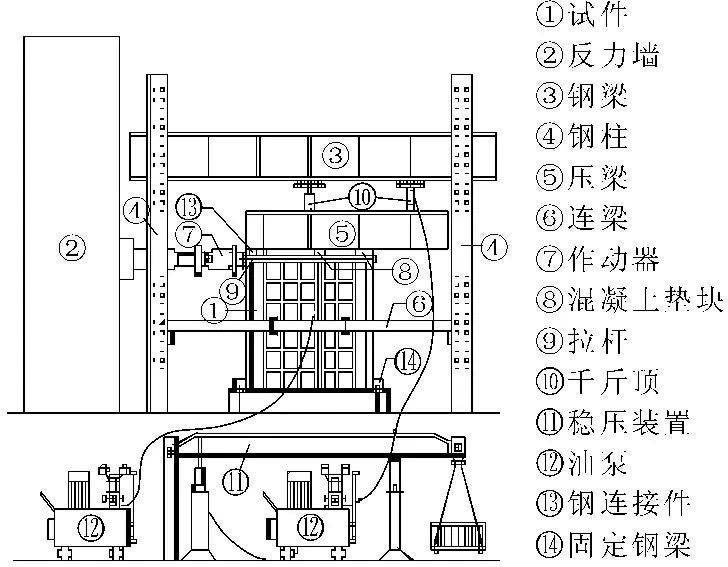
图2 试验加载装置图
该模型总竖向荷载为950 kN,分三级施加,每级为总竖向荷载的1/3,竖向荷载稳定后加水平荷载和附加弯矩,水平荷载每级取10 kN,偏心力荷载按照二者的对应关系增加。试验作用于加载钢梁上的竖向偏心荷载的位置距试件端部0.8 m处。由此可计算出竖向偏心荷载Nm与作用于试件二层顶部水平荷载的关系如下式所示:
(1)
式中:Nm为作用于加载梁上距试件端部0.8 m处的竖向偏心荷载。P为作用于试件顶部的水平荷载。
1.2 试验结果分析
试件参数存在差别,造成各个试件的特征荷载及位移等不相同,但破坏机理、破坏模式一致,均始于受拉侧混凝土竖向约束构件钢筋屈服,终于受压侧混凝土竖向约束构件混凝土压碎和受压钢筋的屈服。墙体特征位移及试件应变情况见表2和图3。
由表2可知试件发生“强板弱柱”型压弯破坏,混凝土竖向约束构件截面尺寸、纵筋配筋率对提高复合墙体的延性及变形性能具有一定作用,但设计时,应注意混凝土竖向约束构件、墙板匹配关系。
由图3可知:
(1) 开裂阶段扣除竖向荷载产生的压应变,钢筋的拉应变和压应变在数值上基本相等,沿截面高度的变化趋势也基本相似,表明两侧混凝土竖向约束构件在弹性阶段承担由弯矩产生的轴力基本相等。
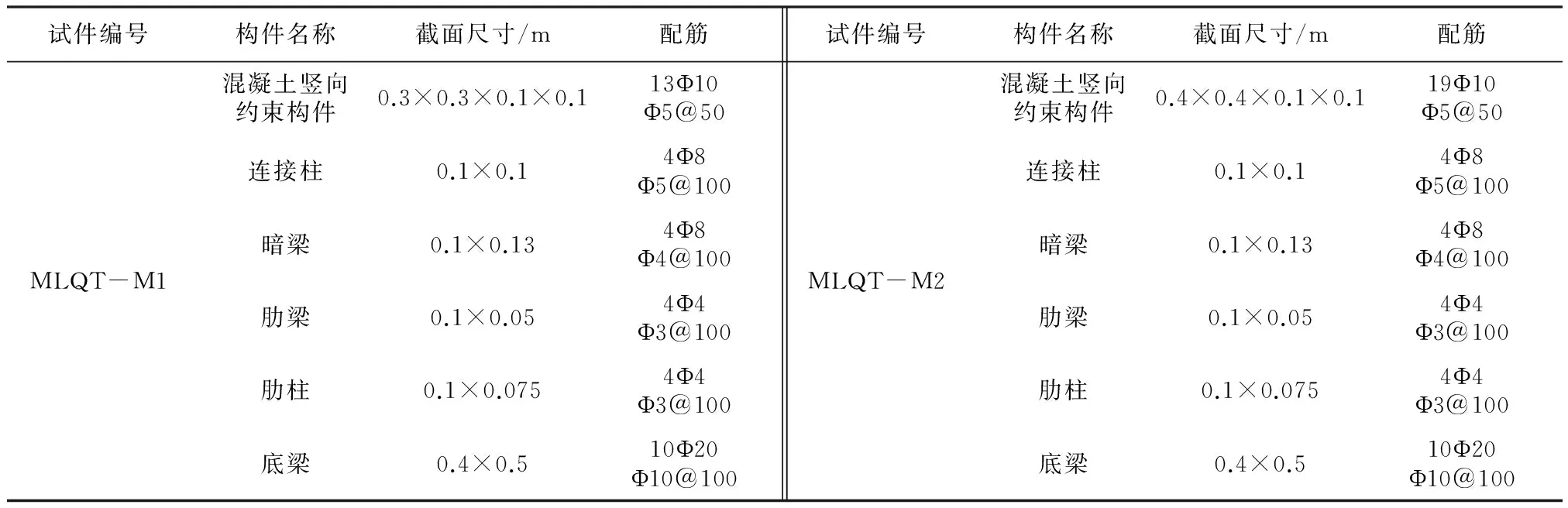
表1 试件的截面特性及配筋

表2 墙体特征荷载和特征位移

注:图中符号:Pcr为开裂荷载;Py为屈服荷载;Pu为最大荷载
图3 试件钢筋应变分析
(2) 竖向约束构件对墙体压弯承载力的贡献主要由竖向约束构件截面的钢筋及受压侧混凝土提供。墙体端部钢筋受力大于其中部钢筋受力,墙体达到压弯破坏极限状态时,受压侧竖向约束构件截面外边缘压应变达到极限应变,该位置处受压钢筋一般情况下可达到屈服,而受拉侧竖向约束构件截面靠近外边缘钢筋可达到屈服或未屈服(取决于墙体的弯曲破坏形态)。影响竖向约束构件对墙体压弯承载力贡献大小的主要因素有:竖向约束构件的截面尺寸、钢筋数量(配筋率)及其布置方式、混凝土强度等。
(3) 肋柱分布于墙体截面的受压区及受拉区。肋柱的纵向受力钢筋不连续,其承担拉力能力有限,故在受拉区只考虑竖向约束构件的纵向受力钢筋。肋柱对墙体压弯承载力的贡献主要是受压区肋柱。
(4) 加气砌块是脆性材料,其抗拉强度远小于其抗压强度,砌块对墙体压弯承载力的贡献主要由受压区内的砌块抗压提供。
2 墙体正截面承载力计算的简化
2.1 正截面承载力计算基本假定
(1) 中高层生态复合墙体正截面符合平截面假定。随着高宽比的增大,墙体破坏逐渐向弯曲型过渡,墙体底面应变逐渐形成较规则的直线;当高宽比达到一定程度而使结构发生弯曲为主的破坏形态时,整个墙体底面的应变基本符合平截面假定。
(2) 受压区混凝土截面只考虑竖向约束构件及端部肋柱,其余受压肋柱均等效成砌体材料。
(3) 竖向约束构件的尺寸相对墙体较小,故假定竖向约束构件均匀受压,其应变取竖向约束构件形心处的应变值。
(4) 装配整体式的构造特点,使得肋柱的纵向受力钢筋不连续,故在受拉区只考虑竖向约束构件的纵向受力钢筋。
(5) 混凝土、加气砌块均是脆性材料,其抗拉强度远小于其抗压强度,混凝土、砌块拉应力的合力距中和轴的内力臂很小,故在计算中高层生态复合墙体正截面压弯承载力时不考虑混凝土、填充砌块的抗拉强度。
(6) 材料的应力应变关系:
① 混凝土应力-应变关系[11]:
(2)
式中:fc为混凝土轴心抗压强度;εc0、εcu分别为混凝土的峰值应变、极限应变;n为系数,按照文献[12]计算。
② 砌块应力-应变关系[11]:
(3)
式中:fq为加气混凝土砌块轴心抗压强度;εq0、εqu分别为加气混凝土砌块的峰值、极限应变。
③ 钢筋应力-应变关系[11]:
(4)
中高层生态复合墙体正截面压弯承载力的简化计算模型如图4所示。
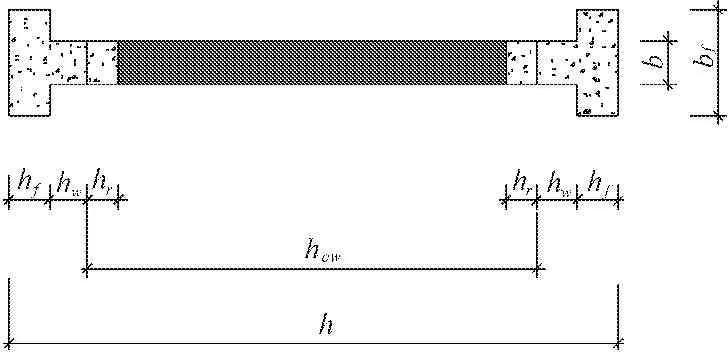
图4 墙体正截面压弯承载力简化计算模型
2.2 等效矩形应力图形
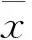
(1) 受压区混凝土。竖向约束构件及端部肋柱尺寸相对较小,故假定受压区混凝土均匀受压,且达到抗压强度fc。
(2) 受压区砌块。当x>hf+hw+hr时,假定受压侧砌块与受压区混凝土边柱相交处的应力达到砌块的极限抗压强度fq,受压区砌块的曲线应力图形等效为矩形。
(5)
(6)
如图5所示,计算求得α1=0.9、β1=0.8。

图5 等效矩形应力图形
2.3 界限受压区高度xb
在弯矩和轴向压力的共同作用下,中高层生态复合墙体相对偏心距及受拉竖向约束构件纵向钢筋的配置决定了墙体的破坏形式。中高层生态复合墙偏心受压时的正截面破坏形态分为大偏心受压破坏(拉压破坏)和小偏心受压破坏(受压破坏)两大类。两种破坏形式间存在一种界限状态:受拉侧竖向约束构件纵向受力钢筋屈服,同时受压侧与肋柱相邻的砌块变形达到极限压应变,这种界限状态称为界限破坏。
根据应变平截面假定,界限破坏时的实际受压区高度xb可按下列公式计算:
(7)
(8)
式中:xqb是墙体发生界限破坏时,砌块的受压区高度;εqu是与受压侧肋柱相邻的砌块的极限压应变;hz是受拉侧竖向约束构件截面形心距离受拉边缘的高度;εy是钢筋的极限拉应变;Es是钢筋的弹性模量。
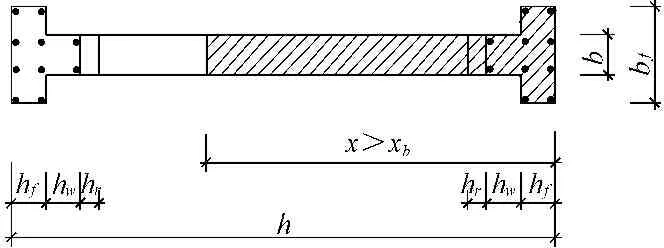
中高层生态复合墙体正截面大、小偏心受压状态判别:当x≤xb时为大偏心受压破坏,x>xb时为小偏心破坏。
3 中高层生态复合墙体的正截面承载力计算公式
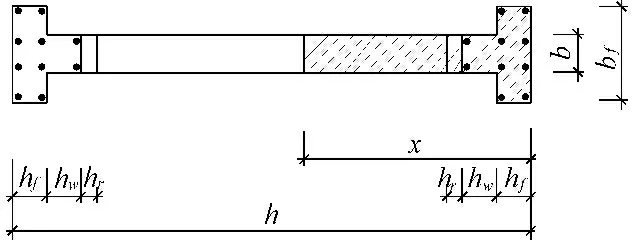
3.1 大偏心受压破坏x≤xb
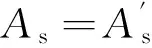
(1)x≤hf。计算简图如图6所示,由纵向受力平衡条件∑Y=0及各力对受拉钢筋合力点取矩∑MAs=0得到正截面承载力简化计算公式为:

图6x≤hf的情况
① ∑Y=0:
(9)
② ∑MAs=0:
(10)
(2)hf 图7hf ① ∑Y=0: (11) ② ∑MAs=0: (12) (3)hf+hw 图8hf+hw ① ∑Y=0: (13) ② ∑MAs=0: (14) (4)hf+hw+hr 图9hf+hw+hr ① ∑Y=0: (15) ② ∑MAs=0: (16) 3.2 小偏心受压破坏 (1)x 图10x ① ∑Y=0: N≤fcbfhf+fcb(hw+hr)+α1fqbβ1(x-h′)+ (17) ② ∑MAs=0: (18) (19) (2)x>h-hf-hw-hr。计算简图如图11所示,由纵向受力平衡条件∑Y=0及各力对受拉钢筋合力点取矩∑MAs=0得到正截面承载力简化计算公式为: 图11x>h-hf-hw-hr的情况 ① ∑Y=0: (20) ② ∑MAs=0: (21) (22) 利用式(10)~式(22)计算出的墙体压弯极限承载力结果,并与试验值进行对比分析,分析结果见表3。 由表3可以看出,由本文公式计算出的墙体承载力与试验值符合较好。结果表明:该公式概念明确、计算简单,可用于指导中高层生态复合墙体混凝土竖向约束构件的配筋。 表3 理论计算值与实测值对比 本文推导墙体正截面压弯承载力实用计算公式,并与前期实验验证,可以得到: (1) 中高层生态复合墙体中的混凝土竖向约束构件为墙体压弯承载力的主要承担者;肋柱纵向钢筋竖向不连续、混凝土和砌块抗拉强度低等因素对墙体的压弯承载力贡献较小,故建立墙体正截面承载力计算公式可忽略其作用。 (2) 基于墙体平截面,结合材料本构关系,给出墙体压弯破坏的界限受压区高度,用于判断墙体的压弯破坏的类型小偏压和大偏压。 (3) 利用简化的应力图形和平衡条件,推导出不同破坏类型的墙体压弯承载力计算公式,并通过算例验证的中高层生态复合墙体的正截面的压弯承载力计算方法可行性。理论及结果表明该公式概念明确、计算简化,可用于指导竖向约束构件配筋计算。 [1] 孔祥峰.小高层钢—混凝土混合结构住宅体系抗震性能的研究及配套技术[D].北京:北京建筑工程学院,2008. [2] 郭晓梅.小高层住宅结构体系优化分析[D].天津:天津大学,2007. [3] 李 兵.小高层住宅结构体系的研究与工程应用[D].合肥:合肥工业大学,2009. [4] 张程华,黄 炜,赵 冬,等.基于复合材料力学模型的生态复合墙体研究[J].工程力学,2012,28(9):249-254. [5] 黄 炜,张程华,姚谦峰,等.密肋壁板结构简化计算模型对比分析[J].振动与冲击,2009,28(7):187-191. [6]LiuP,YaoQF.Dynamicreliabilityofstructures:theexampleofmulti-gridcompositewalls[J].StructuralEngineeringandMechanics, 2010,36(4):463-479. [7] 赵 冬,张程华,黄 炜,等.生态复合墙体的极限承载力分析[J].工业建筑,2012,42(12):56-59. [8] 黄 炜,姚谦峰,章宇明,等.内填砌体的密肋复合墙体极限承载力计算[J].土木工程学报,2006,39(3):68-75. [9] 李元齐,刘 飞,沈祖炎,等.S350冷弯薄壁型钢龙骨式复合墙体抗震性能试验研究[J].土木工程学报,2012,45(12):83-90. [10] 王爱民.中高层密肋壁板结构密肋复合墙体受力性能及设计方法研究[D].西安:西安建筑科技大学,2006. [11] 过镇海,时旭东.钢筋混凝土原理和分析[M].北京: 清华大学出版社,2003. [12] 梁兴文,王社良,李晓文.混凝土结构设计原理[M].北京:科学出版社,2003. [13] 姚谦峰,荆 罡,黄 炜,等.小高层密肋壁板结构复合墙体抗弯性能试验研究[J].西安建筑科技大学学报(自然科学版),2007,39(4):457-462. Analysis of Compression Bending Capability of Normal Section for Middle-high Ecological Composite Wall ZHANG Chenghua1,QIU Jisheng1,HOU Piji1,ZHANG Min2,HUANG Wei2 (1.SchoolofArchitectureandCivilEngineering,Xi'anUniversityofScienceandTechnology,Xi'an,Shaanxi710054,China;2.SchoolofCivilEngineering,Xi'anUniversityofArchitecture&Technology,Xi'an,Shaanxi710055,China) In order to enhance the horizontal bearing capacity and improve the seismic performance of the wall, the middle-high ecological composite wall hybrid structure is proposed through the combination of traditional ecological composite wall structure and concrete vertical restraint components. Based on the stress characteristics of the middle-high ecological composite wall under actual comprehension-bending condition and its special structure form, a reasonable simplified calculation model is proposed. On the basis of the flat section assumption, the material constitutive model and geometric relations, the equivalent rectangular stress patterns for bending normal section bearing capacity calculation of high-level ecological composite wall is developed and a practical compression-bending capacity calculation formula of normal section of is derived. The formula is used to analyze the ultimate bearing capacity of the early test. It shows that the formula has a clear concept and simple calculation, which can be used to guide the reinforcement concrete vertical constraint component of the high-level ecological composite wall hybrid structure. middle-high ecological composite wall; compression-bending capacity; balanced depth of compression zone; large eccentric compression; small eccentric compression 10.3969/j.issn.1672-1144.2017.02.028 2016-12-10 2017-01-12 陕西省教育厅科研计划项目(15JK1488);陕西省自然基础研究计划项目(2016JQ5090);省住房和城乡建设厅科学技术计划项目(2014-K11) 张程华(1986—),男,陕西潼关人,博士,讲师,主要从事新型装配式结构体系及工程抗震。E-mail:zch-0819@163.com TU A 1672—1144(2017)02—0144—07


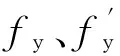
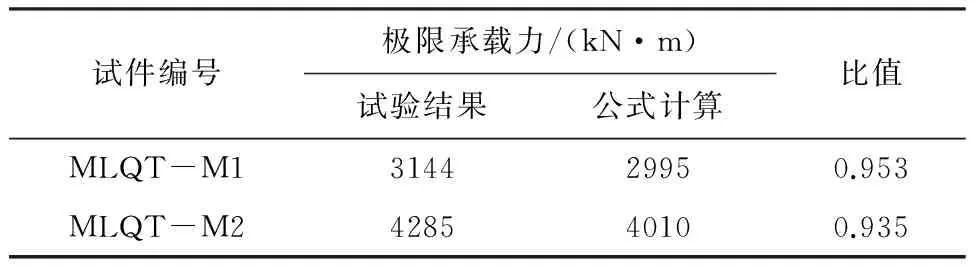
4 模型的验证
5 结 语

