基于Norton方程的岩石蠕变损伤曲线的测定

许 腾，任思玉，樊 成，徐 涛

(大连大学 材料破坏力学数值试验研究中心， 辽宁 大连 116622)

基于Norton方程的岩石蠕变损伤曲线的测定

许 腾，任思玉，樊 成，徐 涛

(大连大学 材料破坏力学数值试验研究中心， 辽宁 大连 116622)

Norton方程通常用于反映金属类材料的稳态蠕变阶段，为了研究Norton方程在岩石材料蠕变损伤的适用性，通过单轴蠕变压缩试验，对同一批试件施加不同轴向应力，绘制不同应力下的时间-蠕变曲线，随着轴向应力的增加岩石出现衰减、稳态及加速蠕变三个阶段。根据Norton提出的经验公式和七点法计算出岩石的应力指数，结合损伤力学理论与Norton提出稳定蠕变和加速蠕变的指数关系，计算出不同时间点的损伤变量，从而绘制出岩石的时间损伤曲线。采用前人提出的损伤模型绘制理论曲线和实验曲线对比，结果表明该曲线符合岩石随时间流变的损伤演化规律，从而得出岩石加速蠕变阶段的损伤曲线符合Norton方程。

稳态蠕变；加速蠕变；损伤；应力指数；时间因子

损伤发生在岩石蠕变过程中的加速阶段，是引起承载力失衡的主要原因。根据损伤力学理论，岩石发生损伤时有两种常用方法定义损伤因子：一种是改变弹性模量，另一种是改变有效承载面积。许宏发[1]通过对软岩进行单轴压缩实验得出随时间增长，软岩的刚度和弹性模量逐渐降低且符合指数曲线。张强勇等[2]在弹性模量劣化的基础上，建立损伤本构模型，认为岩石蠕变模型参数随时间的增长而弱化，直观地反映出岩体的损伤过程。文献[3]在Kachanov损伤演化规律的基础上构建弹塑性损伤元件来描述岩石加速阶段损伤演化。王来贵等[4]建立了单轴和三轴岩石应力应变的非线性损伤模型，根据软岩加速蠕变阶段的特性，编写有限元程序模拟软岩的损伤阶段。蒋昱州等[5]对岩石三个阶段进行力学分析，认为岩石在前两个阶段存在非线性硬化现象，从第三个段开始，岩石发生损伤并呈现非线性特征。郑战光等[6]对岩石进行双轴压缩，用数值方法对其进行数值模拟，提出了岩石由微观损伤发展至宏观断裂的过程，并且证明了非线性黏弹塑性损伤模型的正确性。刘立等[7]在对岩体的损伤与破坏中引入了损伤变量及扩展系数，建立了损伤演化方程，并解释了岩石的损伤演化规律。刘桃根等[8]在Burgers模型的基础上，利用损伤原理，建立改进Kachanov蠕变损伤模型、应变控制蠕变损伤模型和统计损伤模型，并验证了砂岩适用于所改进的模型。黄明等[9]在泥质粉砂岩蠕变特性的试验研究结果的基础上建立蠕变模量和不同含水率的数学表达式，将含水损伤分为瞬间损伤和长期损伤，根据实验结果确定损伤变量和损伤演化方程，并且在泥质砂岩非线性蠕变方程的基础上建立了含水岩石蠕变本构方程。杨圣奇等[10]结合有效应力的观点建立了岩石非线性损伤流变模型，通过对不同围压蠕变试验进行模拟，验证了该流变损伤模型能够较好的描述岩石的衰减、稳态、加速蠕变三个阶段。宋勇军等[11]基于初始屈服强度和长期强度引入能反映岩石的硬化函数和损伤效应的损伤变量，建立非线性蠕变力学模型，并且证明了该非线性力学模型不仅能够很好的反映岩石蠕变过程还可以反映蠕变过程中的蠕变硬化和损伤软化机制。吴斐等[12]根据牛顿阻尼元件提出分数阶非线性黏壶元件，通过该元件建立了新的蠕变本构模型，实验证明非线性蠕变本构模型可以反蠕变映全过程的特征，尤其是非线性加速阶段。宋勇军等[13]通过将含分数阶倒数的软体元件与虎克串联，并引入能够反映应力水平和时间的损伤变量，提出一种四元件非线性蠕变损伤模型。蔡煜等[14]为了使Burgers模型能够描述岩石的加速阶段，采用非常定黏性元件代替Burgers模型中的定常数元件。王军保等[15]通过引入Kachanov蠕变损伤演化规律，构建了可反映岩石瞬时弹性阶段和加速蠕变阶段的时效损伤弹性元件，建立了二元非线性蠕变损伤模型同时验证了其合理性。吴祝林等[16]通过引进弹塑性损伤元件和Kelvin元件模型，建立了三维改进的Kelvin蠕变损伤模型，并推导了三轴压缩情况下的蠕变方程。王其虎等[17]引入初始损伤影响因子，建立具有初始损伤的岩石损伤变量演化方程，构建模拟岩石加速蠕变的蠕变损伤体元件。王晓波等[18]结合微积分理论，建立了考虑损伤的蠕变本构模型并通过实验对模型进行了验证。牛双建等[19]通过实验研究表明损伤岩样各瞬时变形模量随着应力水平的增加均逐步提高，且符合线性函数关系。田洪铭等[20]根据蠕变损伤因子，对ABAQUS软件自带的蠕变模型进行修正，得到了非线性蠕变损伤模型。袁靖周[21]在岩石损伤和蠕变形式的基础上，建立了一种新的岩石长期强度方法并得出岩石长期强度与屈服极限的比值与瞬弹性模量与黏弹性模量的比值有关。谢文光[22]根据Kachanov损伤理论对常规黏塑性体进行改进并与Poyting-Thonson体串联，建立岩石流变损伤模型，利用砂岩蠕变实验对其进行了验证。梁小勇等[23]采用应变等效理论推导的时间硬化蠕变方程并进行了参数拟合和分析。文献[24-26]说明了强度折减法适用于边坡稳定性分析，采用强度折减法对边坡算例进行了稳定性分析并对强度折减法适用性进行了验证。刘小军等[27]在不同含水状态下浅变质板岩单轴蠕变特性的试验研究结果基础上，考虑水对浅变质板岩蠕变参数的劣化效应，其研究表明了含水率对弹性模量和黏滞系数的影响。李佳珑等[28]通过推演三维流变本构方程并引入Kachanov损伤演化方程建立了广义Kelvin模型的三维流变损伤本构模型，通过三轴流变试验结果的模拟验证了该模型的有效性。

本文在有效应力定义的损伤因子的基础上，根据Norton方程得到岩石蠕变损伤因子，可以更简单的确定岩石的损伤曲线，并利用岩石蠕变模型验证损伤曲线的正确性。

1 蠕变损伤理论

时效变形作为岩石的力学特性之一，与岩石的长期稳定性密切相关，岩石长时间在外部荷载的作用下，会造成部分面积承载失效，随着承载力的增加和时间的增长，材料内部失效面积将进一步扩大，直至造成材料完全失去承载力，因此岩石破坏的主要原因是岩石内部微破裂造成的损伤。袁海平等[29]通过实验和研究表明，只有应力大于岩石的屈服极限时，岩石才会发生损伤。岩石材料在不适合的环境条件下，材料内部的微观裂纹、微观空洞的扩大将造成材料的局部破坏。Lemaitre J[30]提出材料的受损变形无论是由单轴或多轴引起的，只需将有效应力替代其中的应力即可，在受荷载作用和时间因子的影响下，岩石材料内部真实受力面积将发生变化，根据损伤力学[31]，名义应力与有效应力的关系为

(1)

式中：σt为有效应力；ω为损伤因子，对于岩石材料无损时ω=0，当岩石材料完全丧失荷载的承载能力时ω=1，此时表示材料完全受到破坏。

(2)

在稳定蠕变阶段岩石发生应力屈服，在此阶段蠕变速率进入线性阶段，其蠕变速率不随时间的增长而变大，最直观的现象是时间-速率曲线的斜率几乎不变化，如图1所示，可以直接分辨恒载作用下的稳态蠕变阶段。

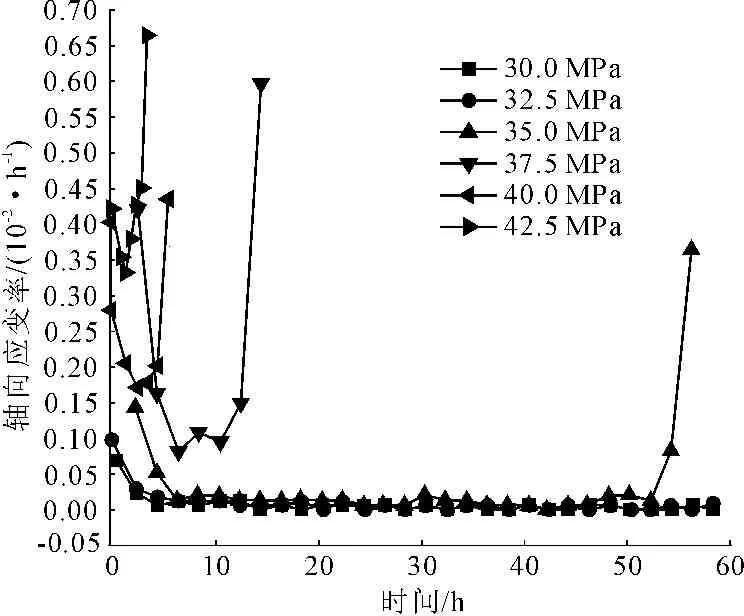
图1 砂岩轴向应变速率与时间曲线

在此前两个阶段，在荷载作用下材料内部没有发生破坏，即损伤因子ω=0。张忠亭等[35]认为传统的方法对岩石加速蠕变阶段研究有局限性，对加速蠕变阶段的开始和结束时刻不好掌握。岩石从第三阶段开始受到破坏，其有效面积、刚度和强度都下降ω≠0 ，其蠕变速率呈指数形式增加，其蠕变应变率和有效应力满足Norton方程：

(3)

由式(2)和式(3)推导出损伤因子公式：

(4)

岩石的蠕变损伤量是用式(4)完成的，也就是通过稳态蠕变阶段的应变率和加速蠕变阶段的应变率间接完成。

2 岩石蠕变损伤曲线的测定

蠕变是岩石材料在保持应力不变的条件下，应变随时间延长而增加的现象。它与弹性变形不同，当所受的应力长时间超过岩石的弹性极限，岩石才会发生蠕变，岩石蠕变曲线是反映岩石在荷载的作用下，时间和应变之间的关系。测量方法就是利用仪器装置直接测其在不同荷载的作用下随时间的增加而改变的应变量，继而根据上述公式(4)推导出损伤值。

本实验在正常的室温条件下进行，蠕变实验在岩石流变冲击试验机上进行单轴压缩蠕变实验，见图2。实验机轴向蠕变采用钢片的全桥应变片(2个轴向，2个径向)进行蠕变测量，可以精确测量2%～3%的变形，仪器为液压输出，最大轴向输出轴向应力为1 000kN。

图2 岩石流变冲击试验机

对岩石进行现场取样，及时腊封后送至实验室进行加工，实验试件加工成φ50 mm×100 的标准圆柱试件，实验分为6组，轴向荷载30.0 MPa、32.5 MPa、35.0 MPa、37.5 MPa、40.0 MPa、42.5 MPa，对试件进行恒载实验，通过应变片记录蠕变值，时间间隔为2 h。

由实验曲线图3可知当施加轴向荷载为30.0 MPa和32.5 MPa时，砂岩蠕变曲线只出现衰减蠕变和稳态蠕变，轴向荷载为35.0 MPa和37.5 MPa时，蠕变曲线出现衰减蠕变，稳态蠕变和加速蠕变三个阶段，而当施加的轴向荷载达到40.0 MPa时，蠕变曲线只存在加速蠕变阶段。并且由图3中的曲线对比可知随着荷载水平的增加，瞬时应变逐渐增加。衰减阶段的曲线半径逐渐增加，进入稳态蠕变阶段所需要的时间逐渐增加，稳态蠕变越来越大且蠕变应变率越来越大。

图3 试样蠕变曲线

根据Norton方程，蠕变应力指数是计算损伤值必不可少的量，对式(2)两端取对数并求导得公式

(5)

(6)

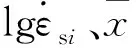
利用软件对n值进行分段拟合并分析(R2至少大于0.95，故舍去D拟合直线)求得出n值为6.63。

表2 方差分析表

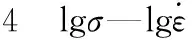
表2中的样本方差为均方和除以相应的自由度，表中的回归平方和比残差平方和更大，故回归分析法得出直线具有较高的准确性。

损伤曲线能更好的反映出试样在荷载的作用下其内部发生的微观破坏，而稳态蠕变阶段和加速蠕变阶段是求损伤量必不可少的条件，要求蠕变曲线明显的存在三个应变阶段，应力没有足够大则试样不会出现加速蠕变阶段，应力过大时试样的蠕变曲线会直接呈现加速蠕变。根据已经得到的蠕变硬化n值和公式(4)计算出损伤因子ω，把已经计算出的损伤因子和发生损伤时的时间因子组成数据(ti/t，ω)，可以绘制出在时间的作用下所发生损伤曲线图。其中ti为实验时间，t为试样开始发生损伤到完全破坏的时间。时间损伤图如图5所示。

图5 砂岩蠕变损伤曲线

3 损伤曲线验证

根据图1和图3可知砂岩试样在加速阶段发生损伤，符合文献[3]提出的岩石在加速阶段发生损伤演化的理论，构造蠕变损伤体，本文根据其提出的理论建立蠕变模型，见图6。

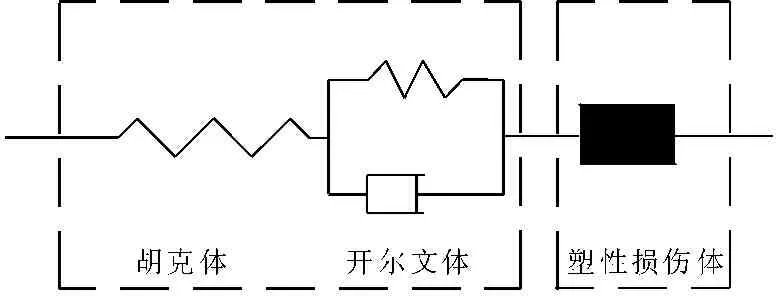
图6 岩石蠕变模型

根据其模型岩石蠕变存在以下特征：

(1) 当σ<σs时岩石只出现瞬时变形和初始蠕变和等速蠕变阶段时岩石蠕变模型蜕化为广义开尔文体其蠕变公式为：

(7)

(2) 当σ≥σs时岩石蠕变出现加速阶段，蠕变模型为广义开尔文模型和损伤体的串联体，蠕变公式可写为：

(8)

本文在蠕变模型的基础上，根据实验数据对参数进行反演，其参数见表3，并根据反演得到的参数进行蠕变曲线拟合，见图7，结果表明其损伤曲线的正确性。

表3 蠕变参数表

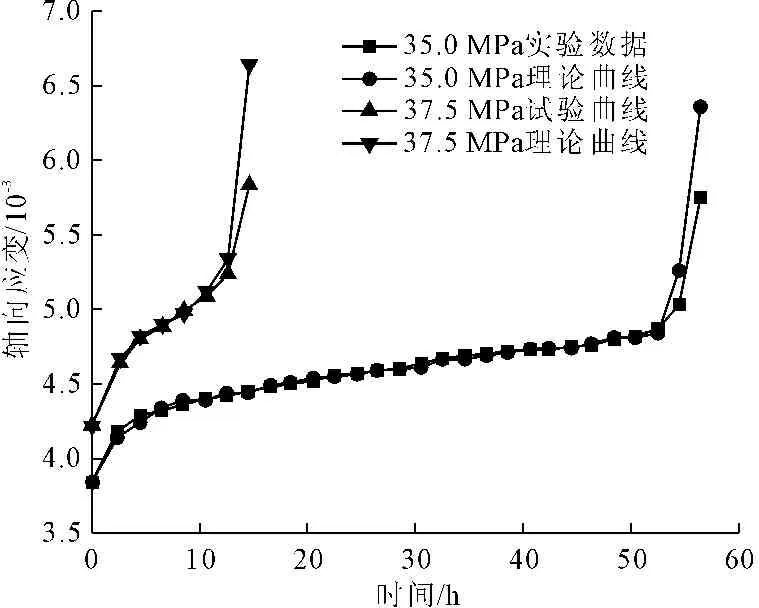
图7 砂岩实测与理论蠕变曲线

4 结 论

本文基于对不同应力水平下岩石试样的蠕变实验，根据Norton方程利用七点分析法分析计算了不同应力水平对岩石蠕变损伤的影响。研究结果表明蠕变应力水平对岩石蠕变应变率及蠕变破坏时间有很大的影响。当施加应力水平较低时，应力对岩石的蠕变损伤影响很小，如果应力水平处于稳态蠕变阶段时，应力水平对蠕变损伤有很大的影响，较小的应力增加能引起破坏岩石的内部结构的较大变化，从而使之更容易达到加速蠕变阶段并导致失稳破坏，具体表现为岩石蠕变应变率增加及蠕变失稳破坏时间降低。本文利用Norton方程根据损伤量与时间的关系画出损伤时间图，计算岩石的损伤量，便于数学计算。

[1] 许宏发.软岩强度和弹模的时间效应研究[J].岩石力学与工程学报,1997,16(3):246-251.

[2] 张强勇,杨文东,张建国,等.变参数蠕变损伤本构模型及其工程应用[J].岩石力学与工程学报,2009,28(4):732-739.

[3] 曹文贵,袁靖周,王江营,等.考虑加速蠕变的岩石蠕变过程损伤模拟方法[J].湖南大学学报(自然科学版),2013,40(2):15-20.

[4] 王来贵,赵 娜,何 峰,等.岩石蠕变损伤模型及其稳定性分析[J].煤炭学报,2009,34(1):64-68.

[5] 蒋昱州,徐卫亚,王瑞红,等.岩石非线性蠕变损伤模型研究[J].中国矿业大学学报,2009,38(3):331-335.

[6] 郑战光,蔡敢为,李兆军.一种新的疲劳损伤演化模型[J].工程力学,2010,27(2):37-40.

[7] 刘 立,马时强,陈 睿,等.岩体损伤与破坏过程研究[J].西华大学学报(自然科学版),2007,26(6):77-79，82+114.

[8] 刘桃根,王 伟,吴斌华,等.基于损伤力学的砂岩蠕变模型研究与参数辨识[J].三峡大学学报(自然科学版),2010,32(6):55-60.

[9] 黄 明,刘新荣,邓 涛.考虑含水劣化的泥质粉砂岩单轴蠕变特性研究[J].福州大学学报(自然科学版),2012,40(3):399-405.

[10] 杨圣奇,徐 鹏.一种新的岩石非线性流变损伤模型研究[J].岩土工程学报,2014,36(10):1846-1854.

[11] 宋勇军,雷胜友,刘向科.基于硬化和损伤效应的岩石非线性蠕变模型[J].煤炭学报,2012,37(S2):287-292.

[12] 吴 斐,刘建锋,武志德,等.盐岩的分数阶非线性蠕变本构模型[J].岩土力学,2014,35(S2):162-167.

[13] 宋勇军,雷胜友.基于分数阶微积分的岩石非线性蠕变损伤力学模型[J].地下空间与工程学报,2013,9(1):91-95，112.

[14] 蔡 煜,曹 平.基于Burgers模型考虑损伤的非定常岩石蠕变模型[J].岩土力学,2016,37(S2):369-374.

[15] 王军保,刘新荣,邵珠山,等.岩石非线性蠕变损伤模型研究[J].现代隧道技术,2014,51(3):79-84.

[16] 吴祝林,王 伟,朱鹏辉,等.基于Kachanov损伤理论的岩石蠕变模型研究[J].三峡大学学报(自然科学版),2016,38(3):32-35.

[17] 王其虎,叶义成,刘艳章,等.考虑初始损伤和蠕变损伤的岩石蠕变全过程本构模型[J].岩土力学,2016,37(S1):57-62.

[18] 王晓波,万 玲.考虑损伤的岩石非线性蠕变模型[J].科学技术与工程,2016,16(20):1-5，21.

[19] 牛双建,党元恒,冯文林,等.损伤破裂砂岩单轴蠕变特性试验研究[J].岩土力学,2016,37(5):1249-1258.

[20] 田洪铭,陈卫忠,田 田,等.软岩蠕变损伤特性的试验与理论研究[J].岩石力学与工程学报,2012,31(3):610-617.

[21] 袁靖周.岩石蠕变全过程损伤模拟方法研究[D].长沙：湖南大学,2012:43-49.

[22] 谢文光.岩石流变损伤本构模型[J].贵州电力技术,2013,16(10):74-76，37.

[23] 梁小勇,薛晓辉,王虎妹,等.岩石时间硬化损伤蠕变特性[J].辽宁工程技术大学学报(自然科学版),2013,32(4):509-512.

[24] 郑文棠.基于FLAC3D的强度折减法和点安全系数法对比[J].水利与建筑工程学报,2010,8(4):54-57.

[25] 齐小静,石自堂,崔金鹏.基于强度折减法的土石坝稳定性分析及失稳判据选择研究[J].水利与建筑工程学报,2016,14(2):104-108.

[26] 李 红,宫必宁,陈 琰.有限元强度折减法边坡失稳判据[J].水利与建筑工程学报,2007,5(1):79-82.

[27] 刘小军,刘新荣,王铁行,等.考虑含水劣化效应的浅变质板岩蠕变本构模型研究[J].岩石力学与工程学报,2014,33(12):2384-2389.

[28] 李佳珑,徐卫亚,王如宾.基于广义Kelvin模型的三维流变损伤本构模型[J].三峡大学学报(自然科学版),2013,35(1):54-57.

[29] 袁海平,曹 平,许万忠,等.岩石粘弹塑性本构关系及改进的Burgers蠕变模型[J].岩土工程学报,2006,28(6):796-799.

[30]LemaitreJ.Howtousedamagemechanics[J].NuclearEngineeringandDesign, 1984,80(2):233-245.

[31] 余寿文，冯西桥.损伤力学[M]．北京：清华大学出版社，1997．

[32]LemaitreJ.ACourseonDamageMechanics[M].Berlin:Springer-Verlag, 1996.

[33] 蔡美峰，何满潮，刘东燕.岩石力学与工程[M]．北京：科学出版社，2002．

[34] 赵从宝.蠕变损伤曲线的测定[J].物理测试,1986(4):14-15，53.

[35] 张忠亭,王 宏,陶振宇.岩石蠕变特性研究进展概况[J].长江科学院院报,1996,13(S1):2-6.

Determination of Rock Creep Damage Curve Based on Norton Equation

XU Teng, REN Siyu, FAN Cheng, XU Tao

(ResearchCenterforNumericalTestonMaterialFailure,DalianUniversity,Dalian,Liaoning116622,China)

The Norton equation is usually used to describe the secondary creep of metal. In order to verify whether the Norton equation is suitable for the application of rock material creep damage, uniaxial compressive creep tests were performed to obtain creep curves of rock samples under different stress levels. The creep curves exhibited typical three-stage curve including primary creep, secondary creep and tertiary creep. The empirical formula proposed by Hollomon and seven-point methods were adopted to calculate the stress index of rock. Combining damage mechanics theory and the relationship between secondary creep and tertiary creep, the damage curves of rock at different time were derived. According to the damage model proposed by other researchers, the theoretical curves and test curves are compared and the results show that the curve is consistent with the characteristics of rock damage evolution with time. It is concluded that the damage curve of the rock accelerating creep phase follows the Norton equation.

steady state creep; accelerated creep; damage; stress index; time factor

10.3969/j.issn.1672-1144.2017.02.007

2016-11-21

2016-12-31

国家自然科学基金项目(41672301，41172265，51474051)；中央高校基本科研业务费项目(N150102002)

许 腾(1991—)，男，河南商丘人，硕士研究生，研究方向为岩土工程。 E-mail:2395419734@qq.com

徐 涛(1975—)，男，湖北随州人，博士，教授，主要从事岩石、混凝土破裂失稳及相关的固流耦合作用的数值模拟和实验研究工作。 E-mail: Neuxutao@126.com

TU458

A

1672—1144(2017)02—0037—06