混凝土坝运行初期安全监控指标拟定方法研究
罗倩钰,杨 杰,程 琳,赵志明
(1.西安理工大学 水利水电学院, 陕西 西安 710048;2.国电陕西水电开发有限公司, 陕西 西安 710075)
混凝土坝运行初期安全监控指标拟定方法研究
罗倩钰1,杨 杰1,程 琳1,赵志明2
(1.西安理工大学 水利水电学院, 陕西 西安 710048;2.国电陕西水电开发有限公司, 陕西 西安 710075)
针对混凝土坝在运行初期安全监测数据有限、常规大坝安全监控指标拟定方法误差较大的问题,提出基于自助法(Bootstrap)及核密度估计(KDE)理论的大坝安全监控指标拟定方法。通过再抽样构造安全监测数据的自助样本,对扩充后的样本采用核密度估计方法确定监测数据的概率密度函数,在此基础上拟定混凝土坝运行初期安全监控指标。结合仿真算例与某混凝土坝的实测数据,并与置信区间法结果对比分析,结果显示新方法误判率低,表明该方法所拟定的安全监控指标可以作为混凝土坝运行初期识别险情的标准,具有有效性和可行性。
大坝安全监测;监控指标;自助法;核密度估计
许多溃坝事故造成的巨大灾难使人们认识到,对于大坝这种特殊建筑物,必须准确快速地判断其工作和安全性态,从而能够采取措施保证大坝的正常运行。在定性分析的基础上,通过已有的监测数据拟定出量化指标,对大坝运行的警戒或危险状态实施监控预报是有效方法之一。对于混凝土坝而言,一方面由实测的安全监测数据建立模型得出监控指标,另一方面,又利用安全监控指标对实测数据进行分析,判断大坝的运行状况,由此分析得出的结果将会影响后续各项决策。因此,一个合理的大坝安全监控指标拟定方法是通过大坝安全监测实现大坝安全监控的关键因素。现有的监控指标拟定方法主要有数理统计法、极限状态法、结构分析法等[1]。随着计算机的发展,越来越多的计算方法如径向基函数神经网络(RBF)、遗传-偏回归模型(GA-PLSR)、改进粒子群算法(PSO)、最小二乘支持向量机(LSSVM)、优化神经网络(BP)、投影寻踪法(PPA)以及模糊聚类算法(FCM)等被广泛应用于大坝安全监控模型中[2-9]。上述方法取得了一定成效,但均要求监测数据样本充足,以保证统计特征量的计算精度从而建立大坝安全监控模型,这在混凝土坝运行初期及采取人工监测的中小型坝中不是总能够满足的。鉴此,本文引入自助法与核密度估计理论,构建了基于该模型的大坝安全监控指标拟定方法,为小样本下混凝土坝运行状况的评判提供参考。
1 Bootstrap方法基本理论
1979年Efron B等[10]提出的自助法(BootstrapMethod)是在给定训练集中进行有放回的均匀抽样,即每当选中一个样本,它拥有等可能再次被选中并添加到训练集中。Bootstrap方法根据给定的原始样本复制观测信息从而对总体的分布特性进行统计推断,不需任何分布假定。
假设有n个样本Xi服从未知分布F
Xi=xi,Xi~i.i.d.F,i=1,2,…,n
(1)
令X=(X1,X2,…,Xn)和x=(x1,x2,…,xn)分别表示为随机样本和其观测值。若存在一个随机变量θ=S(X),它可能既依赖于观测值x,也可能依赖于未知分布F。在以观测数据x为样本的基础上估计θ的分布。
Bootstrap方法主要步骤如下[11]:
步骤1 从F中有放回的随机抽取n个样本。
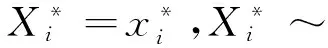
(2)
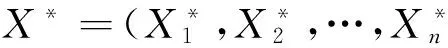
步骤3 从X有放回的随机抽取,生成B个相互独立的自助样本X*1,X*2,…,X*n。
(3)
2 基于KDE的监测数据分布函数估计
2.1 核密度估计基本原理
由Martin等[12]提出的核密度估计(KDE)是一种估算随机变量分布的常用方法,属于非参数检验方法之一。
KDE方法采用核函数κ(·)来拟合数据的分布函数。核函数的实质为权函数,其形状和值域控制着估计在点x值时所利用数据点的个数及程度。对于一维随机变量分布函数,可以采用以下形式进行估计:
(4)
式中:n为样本个数;h为带宽,也称光滑参数或时窗宽度;xi是第i个监测数据。本文将扩充后的监测样本在MATLAB中实现KDE方法以估计其概率密度函数。
2.2 带宽选择
一般而言,选择任何形式的核函数都能保证密度估计具有稳定相合性。而带宽值则对估计量的影响较大,若h太小,则密度估计偏于将概率密度分配局限于观测数据附近,致使密度函数产生错误峰值;若h太大,密度估计则将概率密度贡献扩展分散,导致光滑掉F的重要特征[13]。带宽选择一般需遵循以下最优原则:
选择带宽h常用的方法是极小化均方误差法:
(5)
当分布密度连续时常用极小化积分均方误差法:
(6)
以及极小化渐进积分均方误差法:
(7)
其中,极小化积分均方误差法可分解如下:
(8)
上式中期望和方差都是针对于样本描述的。σmise依赖于带宽h和函数f的选取,在渐进逼近的方法下得到简化,即σamise[14]。在一致性要求下,取决于样本容量的大小,一般随样本容量n的增大而减小,则渐进最优带宽为σamise的最小值。
本文通过MATLAB实现在高斯核函数下自动选取最优带宽。
3 监控指标的拟定
不同于假设监测效应量样本服从正态分布的各传统监控指标拟定方法,本文将Bootstrap方法和KDE方法相结合,确定出监测变量E的概率密度函数f(E)。令Em为某项监测数据的安全监控指标,则当E>Em时,大坝将出现异常或险情。其概率为:
(9)
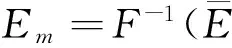
综上,混凝土坝运行初期安全监测数据分析与监控指标的拟定流程如下:
步骤1 由原始观测数据,计算大坝位移观测量的监测值,根据统计分析方法原理,剔除实测数据中的粗差;
步骤2 将监测数据采用Bootstrap方法扩充其样本容量,构造监测数据的自助样本;
步骤3 由核密度估计方法估计监测数据大样本的分布情况及其概率密度函数,利用小概率原理拟定相应监测项目的安全监控指标;
步骤4 由所拟定的安全监控指标确定监测数据中的异常测值,分析其成因,判定大坝安全性态是否出现突变以及大坝监测系统是否稳定可靠。
4 算 例
4.1 仿真验证
本文提出基于Bootstrap和KDE方法的数学模型,为检验其由已知样本点集合求解随机变量分布函数的有效性及精度,首先由计算机产生符合标准正态分布的测试数据样本100个,具体数据从略。接着从中抽取生成容量不同的5组样本,然后分别采用Bootstrap方法将其转换为大样本(见表1)并采用KDE方法估计其概率密度函数(部分结果见图1),最后与标准正态分布比对以检验拟合程度。
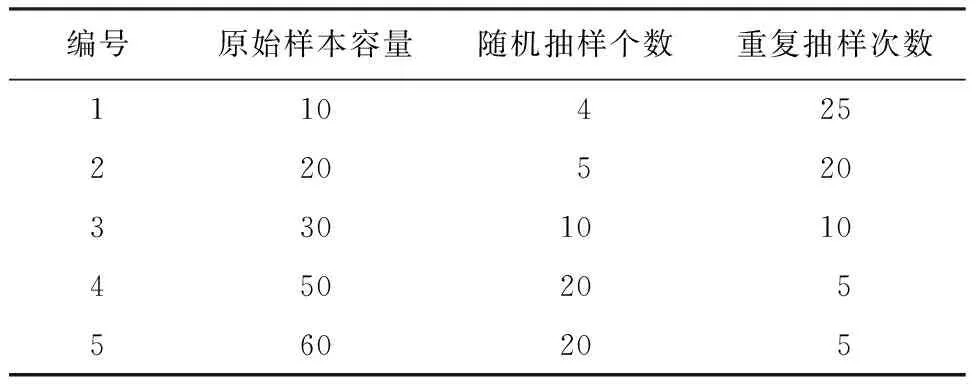
表1 各独立样本的Bootstrap方法实现过程

图1 部分样本概率密度估计图
偏度与峰度分别表征概率密度曲线相对于平均值的不对称程度及平均值处峰值的高低特征,可用于进行正态性检验。对于样本数为n的序列xi(i=1,2,…,n),偏度系数g1和峰度系数g2分别定义为:
(10)
(11)
式中,m2,m3和m4分别为二阶,三阶和四阶中心矩。K阶中心矩可表示为:
(12)
5组扩充后样本的偏度和峰度值计算结果见表2。
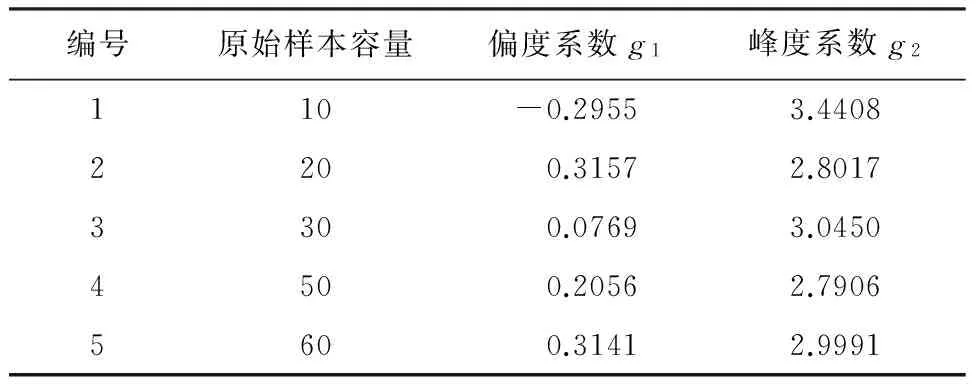
表2 各独立样本的偏度及峰度计算值
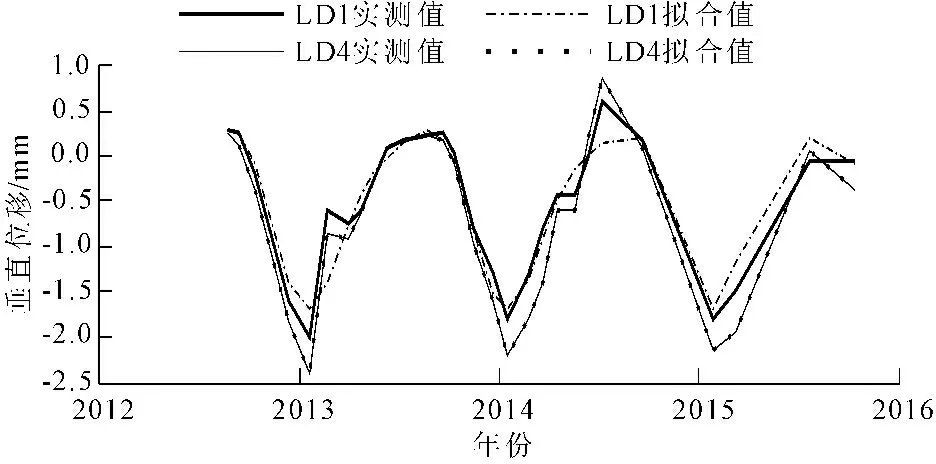
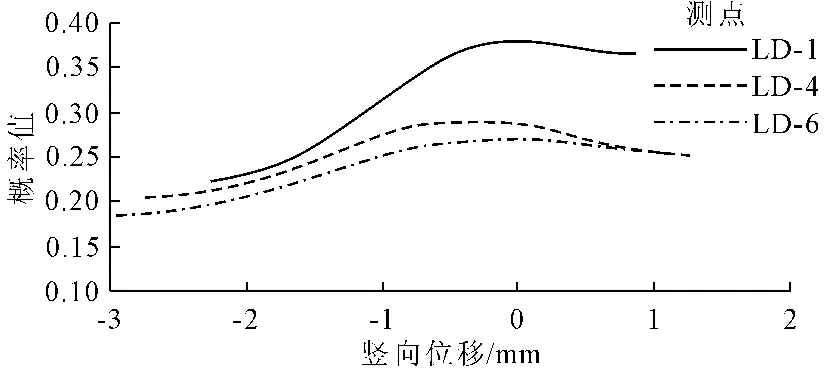
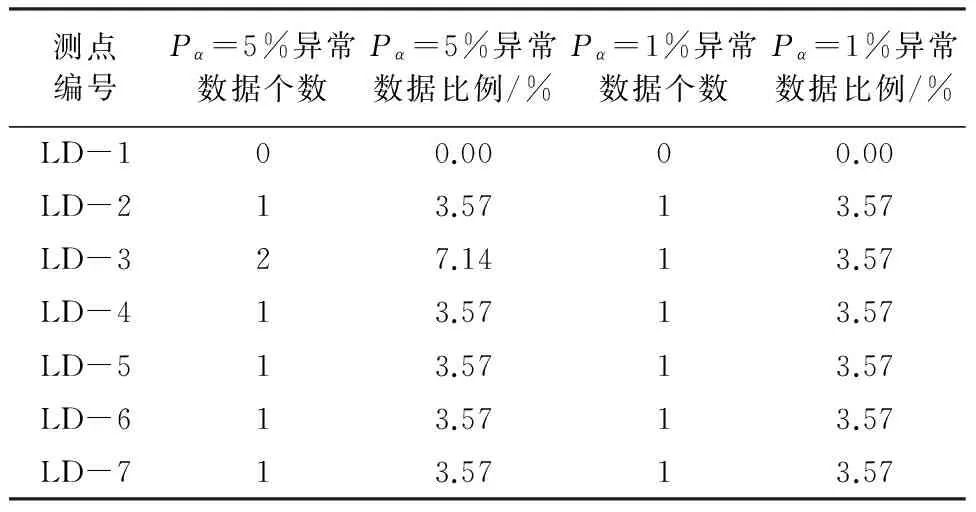
选定α=0.05的显著水平下,确定g1和g2相应的阈值Ug1和Ug2。当|g1| 据仿真验证可知,将Bootstrap和KDE方法结合,能够很好地估计原始样本的数据分布趋势,针对样本容量仅为10的小样本即可运用,提高了样本质量。当原始样本容量增大时,该方法也能够最大程度去除冗余属性,反映数据集的本质特征。 4.2 工程实例 某枢纽工程位于汉中盆地的东域,北居秦岭南坡。本工程等别标准为Ⅲ等工程,由挡水建筑物、引水系统、发电厂房和升压开关站组成。拦河坝为混凝土重力坝,坝顶高程675.7 m,最大坝高40.7 m。为监测和馈控大坝的运行状态,该工程目前设置的大坝安全监测项目为坝体水平及竖向位移监测。大坝竖向位移采用水准线路法进行人工监测。在坝顶675.7 m高程处,沿坝轴线方向,由左至右共布置7个测点,工作基点分别设在左右上坝公路上。竖向位移于2012年8月起测,监测频率为每月1次。监测资料系列为2012年8月23日—2015年10月11日。规定竖向位移方向为:上抬为正,下沉为负。由以上实况可知本次监测资料系列较短,且处于工程运行初期。该工程竖向位移测点平面布置图见图2,坝顶竖向位移典型监测测点实测回归过程线与回归模型拟合情况见图3。 图2 竖向位移测点平面布置图 图3 典型测点实测过程线与回归模型拟合图 采用Bootstrap方法对坝体竖向位移28个监测数据进行扩充。通过MATLAB程序设计,得到包含2800个样本的训练集。计算结果见表3。 表3 原序列与重抽样参数估计结果 由表3可见,由Bootstrap方法扩充后样本的均值及标准差与原序列接近,可知经过Bootstrap方法得到的训练集可信。 区别于其他密度估计实现方式,核密度估计未针对已知数据假定任何参数模型,因此不会产生数据广泛分离或多峰值分布现象。竖向位移核密度估计最优带宽见表4,典型测点LD-1,LD-4,LD-6监测数据概率密度估计图见图4。 图4 典型测点监测数据概率密度估计图表4 各竖向位移测点数据核密度估计的最优带宽 令Em为坝体竖向位移监测上抬量的安全监控指标,则当E>Em时,大坝将出现异常或险情,见式(9)。 下沉方向竖向位移安全监控指标的拟定同理。针对该枢纽工程大坝具体情况,得到7个竖向位移监测测点在失事概率Pα=5%和Pα=1%下的安全监控指标,见表5。 置信区间法根据以往的监测资料,建立监测效应量与荷载之间的数学模型。坝顶竖向位移主要受水压、温度和时效等因素的影响。由参考文献[1],可建立坝顶竖向位移统计模型表达式如下: 表5 各测点竖向位移安全监控指标表 c1(θ-θ0)+c2(lnθ-lnθ0) (13) 以式(13)为目标函数,应用MATLAB统计工具箱,对该枢纽大坝7个竖向位移测点人工监测数据进行逐步回归分析,拟合结果见图3。 (14) 当显著性水平α=1%时,Δ=2.576σ;α=5%时,Δ=1.960σ≈2σ。则其相应的监测效应量的监控指标Em为:Em=E±Δ。 该枢纽电站大坝自有安全监测数据记录以来至今运行近三年,其间没有出现过危及大坝安全的险情,故可认为此前的原型监测数据均为正常数据。将自助法与核密度估计相结合后所拟定的安全监控指标符合这一事实。若以置信区间估计法建立的安全监控指标来评判大坝近年来运行状况,则有3.6%~7.1%的坝顶竖向位移监测数据因超过Em而被评定为异常(见表6),可见其误判率较高。 表6 置信区间法拟定安全监控指标对枢纽 运行状态评价指标表 置信区间估计法拟定的安全监控指标很大程度上取决于进行实测资料分析时所建立的数学模型的拟合效果。在混凝土坝运行初期,由于监测系列较短,建模本身精度不高,拟定的监控指标则无法评判大坝的运行状况。由算例结果可得,新方法所评判的大坝近年来的运行状况符合其正常运行的事实,且所拟定的监控指标与已有监测数据中极值的差值合理,可作为今后混凝土坝运行初期识别险情的标准。 本文提出了混凝土坝安全监控指标拟定的新方法,从监测数据本身出发,将Bootstrap方法和KDE理论相结合,在混凝土坝运行初期监测资料系列较短的情况下利用现有资料对大坝抵御未来荷载的能力进行估计,通过与传统统计模型的对比分析说明,该方法提高了混凝土坝运行初期安全监控指标拟定的准确性。后期可针对方法的通用性进行进一步研究。 [1] 吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社,2003. [2] 程 琳,徐 波.基于云—RBF神经网络模型的大坝监测数据预报[J].水电能源科学,2010,28(6):64-66. [3] 王小军,雷 娜.大坝安全监测的遗传—偏回归(GA-PLSR)模型研究及应用[J].水利与建筑工程学报,2010,8(5):113-116. [4] 张 鑫,王冬利,李 琦,等.基于改进粒子群算法的坝体位移监控模型[J].水利与建筑工程学报,2012,10(1):155-159. [5] 徐 南,陈逸凡,吴 彦.基于交叉验证LSSVM的大坝监测数据处理模型[J].水利与建筑工程学报,2013,11(3):67-69.[6] 李占超,张慧莉,刘兴阳,等.混凝土坝小样本安全监控模型研究[J].中国科学:科学技术,2014,44(10):1043-1051.[7] 王雪红,刘晓青,陶海龙,等.优化BP神经网络的位移预测模型[J].水利水运工程学报,2014(2):38-42. [8] 张云龙,王文明.PPA-CM模型在双曲混凝土拱坝变形监控指标拟定中的应用[J].水电能源科学,2016,34(4):43-46. [9] 张海龙,马 斌.FCM-RVM预警模型在某重力坝典型坝段水平位移预测中的应用[J].水电能源科学,2016,34(5):81-84. [10] Efron B. The jackknife, the bootstrap, and other resampling plans[M]. Society for Industrial and Applied Mathematics,1982. [11] 毛 平.Bootstrap方法及其应用[D].湘潭:湘潭大学,2013. [12] Botev Z I, Grotowski J F, Kroese D P. Kernel density estimation via diffusion[J]. The Annals of Statistics,2010,38(5):916-2957. [13] 屈文建,熊国经.非参数密度估计法比较分析及应用[J].沈阳农业大学学报,2008,39(4):468-472. [14] 李泽中,白 勇.核密度估计在分类问题中带宽参数的优化研究[J].计算机科学,2009,36(6):258-261.[15] 方建刚,毛明策,程肖侠.陕西降水的正态分布特征分析[J].西北大学学报(自然科学版),2009,39(1):131-136. Determination Method of Safety Monitoring Index of Concrete Dams During Initial Operation Stage LUO Qianyu1, YANG Jie1, CHENG Lin1, ZHAO Zhiming2 (1.InstituteofWaterResourcesandHydro-electricEngineering,Xi'anUniversityofTechnology,Xi'an,Shaanxi710048,China;2.GuodianShaanxiHydropowerDevelopmentCo..Ltd.,Xi'an,Shaanxi710075,China) A combined method to determine safety monitoring index for concrete dams based on Bootstrap method and kernel density estimation (KDE) method was proposed to solve the problem that common methods occur errors when monitoring data are limited during the initial operation stage of concrete dams. Through re-sampling to structure the safety monitoring data of the bootstrap samples, the extended samples were then used to estimate the probability density function using kernel density estimation (KDE) method. Thus, the dam safety monitoring index can be determined. Based on the simulation example and the monitoring data of a concrete dam, the proposed method with low misjudgment rate is effective and practicable compared with the traditional method, which can be recognized as a standard to identify dangers in future. dam safety monitoring; monitoring index; Bootstrap method; kernel density estimation 10.3969/j.issn.1672-1144.2017.02.006 2016-12-10 2017-01-08 陕西省重点科技创新团队项目(2013KCT-15);国家自然科学基金项目(51409205) 罗倩钰(1994—),女,广东大埔人,硕士研究生,研究方向为水工建筑物安全监测。 E-mail: m13572157342@163.com TV698.1 A 1672—1144(2017)02—0032—05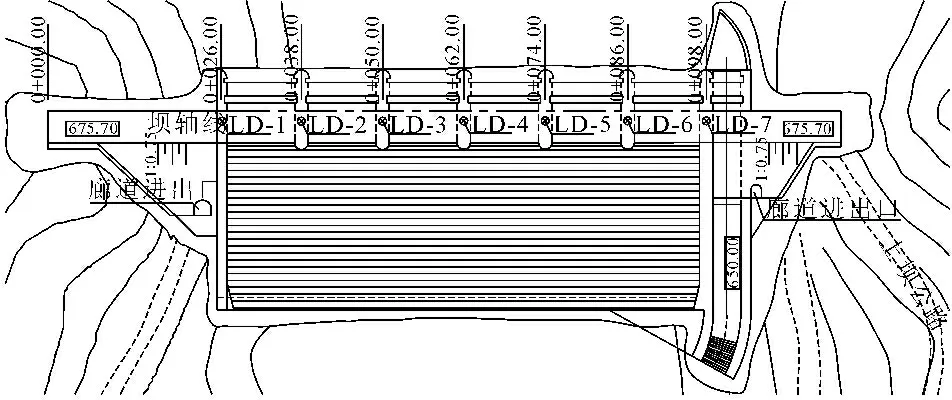



5 结 论

