边界透气性对降雨入渗的影响
郝 霜,童富果,刘 刚,薛 松
(三峡大学 水利与环境学院, 湖北 宜昌 443002)
边界透气性对降雨入渗的影响
郝 霜,童富果,刘 刚,薛 松
(三峡大学 水利与环境学院, 湖北 宜昌 443002)
基于水气二相流理论,采用有限单元法计算了不同透气边界条件下的降雨入渗过程,探讨了边界透气性对稳定入渗强度、孔隙气压分布和饱和度分布等的影响。边界透气条件是渗流计算中的一个重要控制条件,传统计算多为定性研究,通过量化透气条件,分析边界透气性对降雨入渗的影响。结果表明:稳定入渗强度与边界透气性密切相关,边界透气性越小,稳定入渗强度受透气性影响越敏感,其敏感性随边界透气性增大逐渐降低,边界透气性对稳定入渗强度的影响呈对数关系。此外,边界透气性越小,降雨入渗过程中孔隙气压力越大,湿润锋推移速度越慢。
降雨入渗;透气条件;水气两相流;入渗强度
降雨入渗是一个复杂的非饱和水气二相流问题,相关的研究在滑坡治理,城市防洪,保护水土流失等领域应用广泛[1-3]。降雨入渗的本质是水气两种流体的物质传输,渗流过程是水流下渗驱替土体孔隙中空气,孔隙气受压又阻碍水流下渗的过程[4-5]。在物质传输的数值模拟中,物质的进出条件是重要的边界控制条件,控制着物质进出的强度、总量和难易程度[6],因此,在入渗过程的模拟中水、气进出边界条件也对渗流过程起着关键的作用。
非饱和土体渗流的边界问题已有学者做了相关研究,在国内吴良骥等[7]对非饱和渗流问题的研究开展较早,应用有限差分法考虑势边界、Neuman流量边界和自由面的混合边界条件对渗流问题进行了模拟。朱岳明等[8]用有限单元法考虑水相渗流边界条件对三维非饱和渗流场进行了求解。在国外Gabriela Marinoschi[9]基于Richards方程推导了非饱和土体渗流的非线性模型,应用了半渗透的自由边界条件。大多研究都考虑了渗流边界透水性对降雨入渗的影响,但降雨入渗是水、气两种流体在物质传输过程中相互耦合作用的过程,因此研究渗流边界透气性的影响也同样重要。
在渗流边界透气性的研究中大多为定性分析,李援农等[10]利用均质土壤积水入渗的试验,研究了入渗过程中考虑气阻与孔隙气自由溢出的边界透气条件对降雨入渗的影响;张华等[11]采用室内物理试验的方式研究了积水入渗过程中孔隙中封闭气泡阻止渗透的机制和规律;Boris I等[12]基于试验研究的方法探讨了渗流过程封闭气泡含量对稳定入渗率的影响规律。由于试验研究无法定量给出边界透气程度,也无法定量分析边界气相流动对降雨入渗的影响[13],因此本文基于水、气二相流的理论,采用有限单元法建立降雨入渗的数值计算模型,量化边界透气性来分析流量边界上不同程度的透气条件对降雨入渗的影响。
1 水气二相流数值模型
水气二相流控制微分方程是为描述非饱和多孔介质中水、气运动特征而建立的数学模型[14-16]。其基本假设认为土体孔隙是均匀且各向同性的,土、水、气混合物为连续介质,是满足连续介质守恒定律,流速缓慢认为其流动状态为层流且符合达西定律,水气间质量交换忽略不计。根据质量守恒方程与达西定律可得到孔隙中水相非饱和流动方程:
(1)
对于式(1)中第一项,考虑φw=φSr,可展开为
∂t(ρwφw)=φSr∂tρw+φρw∂tSr+ρwSr∂tφ
(2)
考虑水不可压缩,∂tρw=0;不考虑孔隙变形,∂tφ=0。则式(2)可变为
∂t(ρwφw)=φρw∂tSr
(3)
对式(1)中第二项,可展开为
(4)
(5)
不考虑内源,可得到水流动方程微分形式
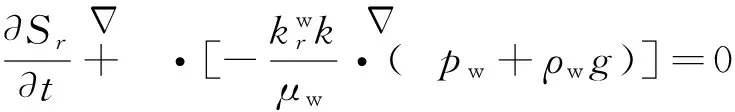
(6)
根据以上方法,不考虑孔隙变形、气体压缩性,可以得到气流动方程
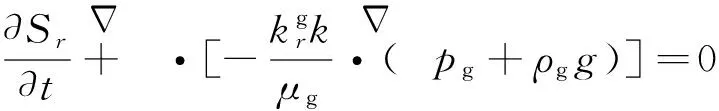
(7)

式(6)和式(7)为非饱和土水气二相流控制微分方程组。
在求解水气二相流方程时,选择孔隙气压力和饱和度作为基本变量。孔隙水压力和孔隙气压力关系可以表示为pw≡pg-pc,pc为基质吸力。方程组的空间离散化采用Garlerkin有限单元法,方便引入边界条件。时间域离散采用一维差分方法,将时间域分为一系列的时段,在每个时段Δt=tk+1-tk内假设变量随时间线性变化。
2 数值模型
2.1 几何模型
本模型为一维均质壤土土柱模型,高3m,计算单元20个,计算网格节点数42个,网格上密下疏,最小单元厚度为0.1m,计算网格模型及尺寸见图1。为控制计算土体边界的渗透性,模型以6号单元底部边界为底部边界,1~5号单元为固定饱和度的土体,用以控制底部边界的透气程度,因此将模型分为上下两部分。假设计算土体为均质各向同性土体,不考虑孔隙变形,假定降雨强度远大于入渗强度,地表层始终处于饱和状态,忽略其地表径流对土体内部入渗过程的影响。
2.2 辅助方程及参数
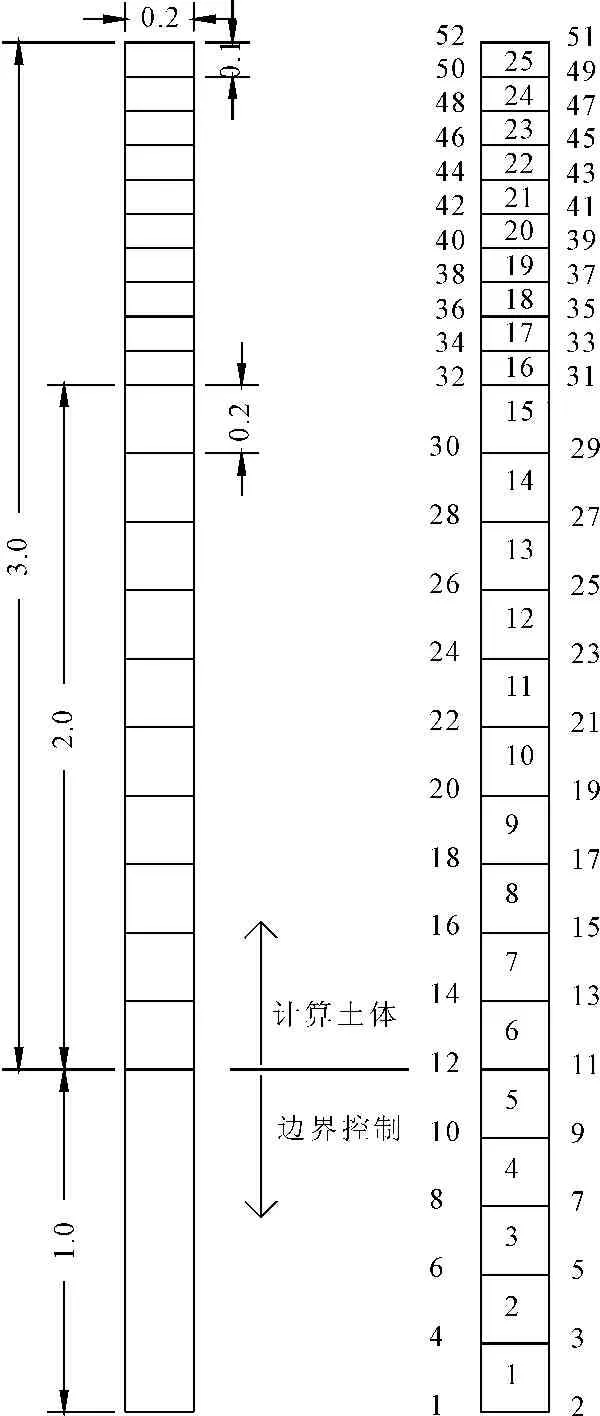
图1 计算区域网格模型及尺寸

土水特征曲线采用Van Genuchten模型(VG模型),为公式(8),模型曲线见图2。

图2 土水特性曲线
(8)
(9)
式中:Se为有效饱和度;Srw为残余水饱和度;n、m为与粒径均匀性有关的参数,m=1-1/n;p0为与材料特性相关的参数。根据相关资料,确定壤土计算参数p0=0.278,m=0.359,Srw=0.1。
液相非饱和渗透系数与饱和度的关系采用Mualem模型,如式(10)
(10)
气相的渗透率函数曲线采用Brooks-Corey模型,为公式(11)
(11)
式中:Srg为残余气饱和度,Srw为残余水饱和度。
土样物理模型参数及VG模型参数见表1,液相与气相渗透特性曲线见图3。

表1 土样物理参数及VG模型参数

图3 土体非饱和渗透特性曲线
2.3 边界条件
土柱整体以同种初始饱和度起算,地表为积水入渗已知流量边界,底部自由流出,地表与底部均为大气压边界,侧边界为不透水不透气边界。因为在自然界中,所有边界的封气条件都不是绝对的,其与边界下土体厚度,饱和度、孔隙率等有关,所以为研究边界不同透气程度对降雨入渗过程的影响,采用边界下单位作用力的气流速作为统一衡量边界透气性的标准,无量纲化为模型下部单位气相流速与上部饱和气相流速的比值,上部饱和气相流速取0.000168m/s,残余饱和度为0.1,气相黏滞系数为1.84×10-5。该透气性标准与计算土柱底边界以下的土柱饱和度正相关,对应关系见表2。

表2 边界透气性对应表
3 渗流边界透气性对降雨入渗的影响
降雨入渗过程是一个涉及水、气两相流动的物理力学过程,影响降雨入渗的主要因素有土体性质及颗粒级配,土体初始饱和度,水力梯度,渗流边界条件和温度等,而其中渗流边界上气相的流动一定程度上影响了水相入渗。本节首先分析了透气性与稳定水相入渗率的相关关系,而后研究了不同边界透气性对入渗过程中土体的孔隙气压力、相对入渗率和不同降雨历时下饱和度分布的影响。
3.1 边界透气性对相对稳定入渗强度的影响
稳定入渗强度是计算土体渗流量,衡量土体入渗能力的重要指标,稳定入渗强度与土体颗粒结构、初始饱和度和透气性等因素有关,其中边界透气条件是自然界中普遍影响入渗强度的因素。本节模拟了土体初始饱和度为0.3时,不同边界透气程度下的相对稳定入渗强度,研究了边界透气性对稳定降雨入渗强度的影响规律(见图4)。
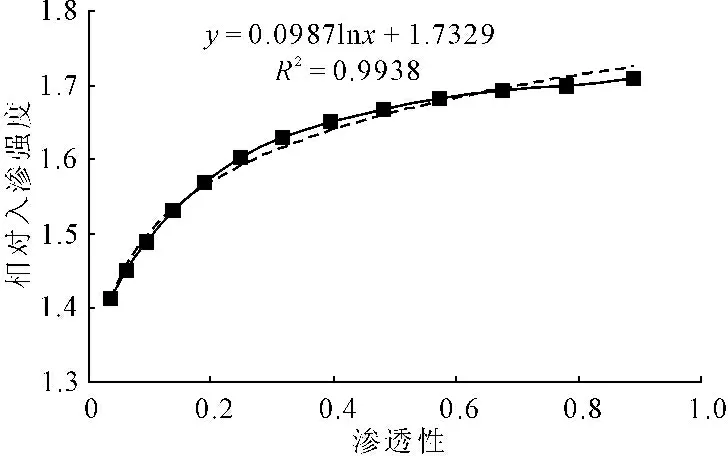
图4 相对稳定入渗强度与边界透气性的关系曲线
相对稳定入渗强度定义为实际水相稳定入渗强度与饱和土体水相稳定入渗强度的比值,取无量纲化的比值更有相对意义的对比性,水相饱和稳定入渗强度取0.01854m/s。由图4 可知,稳定入渗强度随土体边界透气性的增强而增加,稳定入渗强度在土体透气性较小时敏感性较大,随边界透气性增大敏感性逐渐降低,由此边界透气性在较小时对稳定入渗强度的影响较大。以对数函数拟合边界透气性与稳定入渗强度的关系,为y=0.0987lnx+1.7329,拟合确定系数R2为0.9938,由此可以看出对数函数的拟合效果良好。降雨入渗的过程就是土体中水、气两种流体在孔隙中相互交替的过程,气相的流动势必会影响水相的入渗,而在边界透气性较差,气相密封于土孔隙之中时,气相对入渗强度的阻滞作用明显。
3.2 边界透气性对入渗过程的影响
土体入渗强度是降雨入渗过程中重要的土体渗透参数,根据达西渗流定律v=ki,土体入渗强度是由土体饱和渗透系数k与水力梯度i决定的,而饱和渗透系数只与土体本身有关,因此入渗强度基本由水力梯度决定。在降雨入渗初期表层土体饱和度较小,基质吸力较大,水力梯度因此较大,使得降雨初期的入渗强度较大,但随降雨历时增加,土体饱和度增加,基质吸力快速下降,水力梯度也随之快速下降,因此在降雨入渗初期入渗强度下降梯度较大直到相对稳定。在土体表层饱和后,孔隙气被表层饱和土体密封于孔隙之中,随水分不断入渗,孔隙气受入渗水分挤压,使得孔隙气压力快速上升并对水分入渗产生阻滞作用,见图5。在不同的边界透气程度下,水相挤压孔隙气相而产生的孔隙气压力不同。边界透气性越小孔隙气压力增大越快且维持在一个相对较大的水平,气压力消散也较缓慢。边界透气性越小稳定孔隙气压力越大,相应对水相入渗阻力越大,入渗强度越小,见图6,这说明边界透气性影响了阻碍了水分入渗,降低了水相入渗强度。
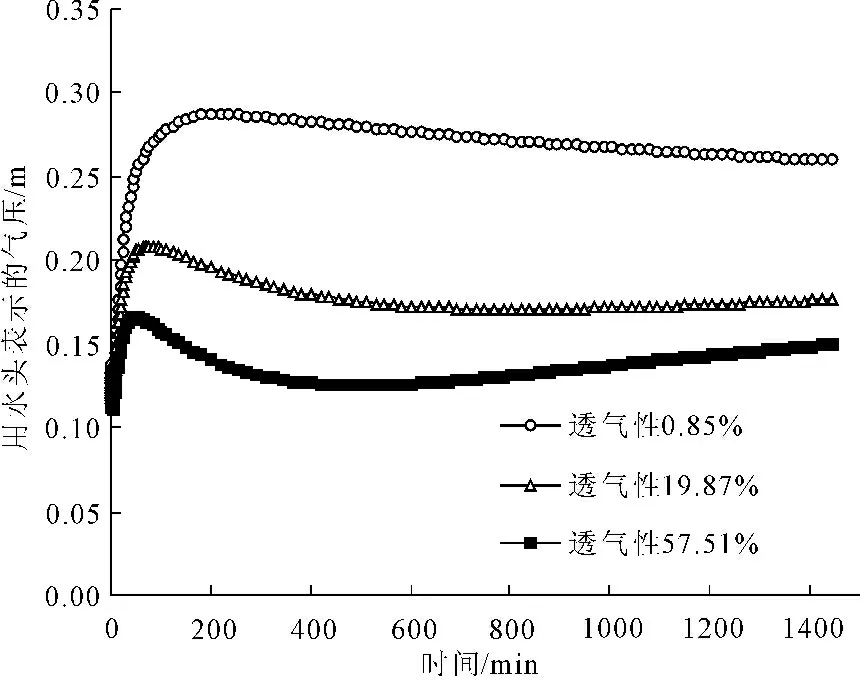
图5 不同透气程度下0.3 m处气压
本节计算了透气性为0.85%、19.87%和57.51%的三种情况在入渗511 min和1005 min时的土体垂直深度处饱和度分布,土体初始饱和度都为0.3,结果见图7(a)、图7(b)。土体垂直深度饱和度分布图显示,随着降雨历时的增加,土体湿润锋随之下移,土体饱和度从表层到深层逐渐增加,入渗面积随降雨历时不断增大。
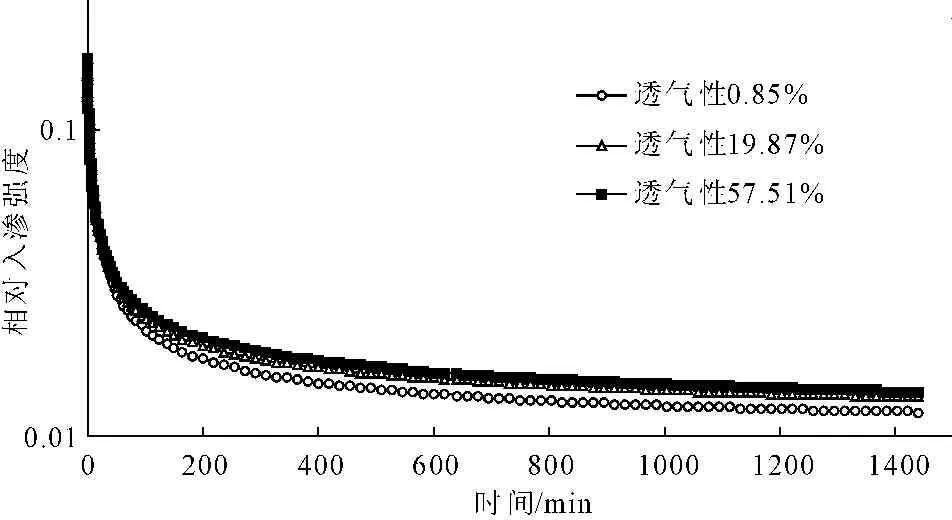
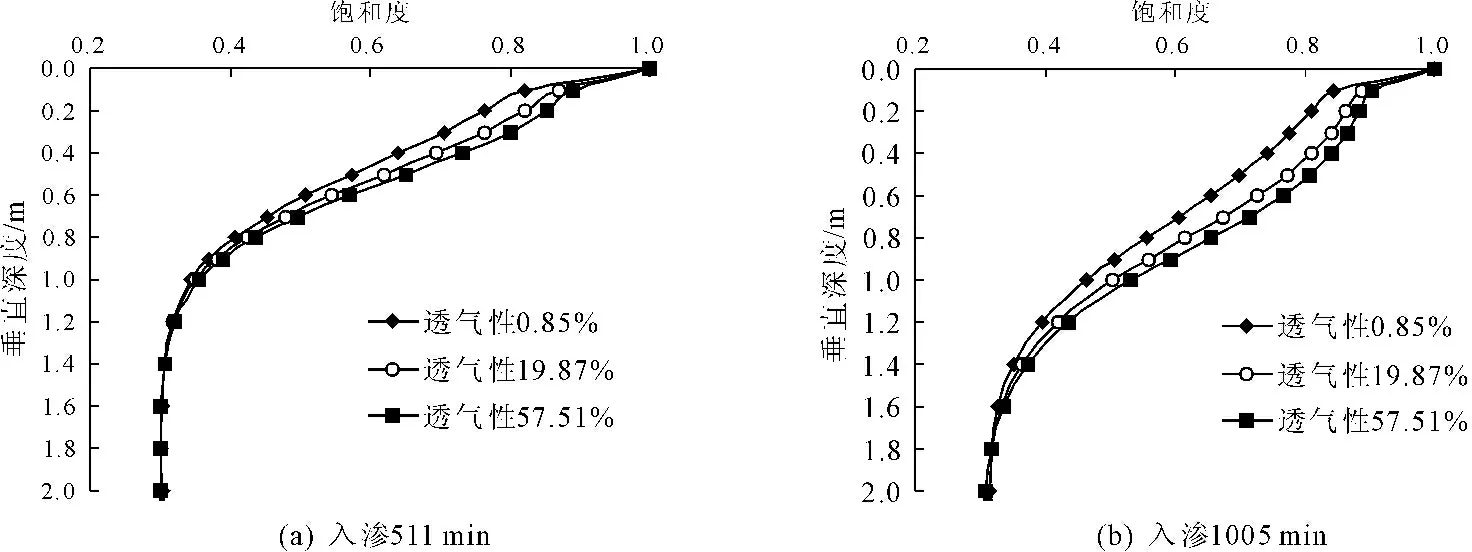
图6 不同透气程度下土体表层相对入渗强度
图7 饱和度分布图
边界透气性对土体饱和度分布的影响在土体浅层相对明显,边界透气性越小湿润锋下降越缓慢,且随降雨入渗历时越久边界透气性的影响越大,这说明入渗强度的降低使边界透气性对累积入渗量的影响随降雨历时的增加逐渐加大,相应的湿润锋也下降缓慢。
4 结 论
基于水气二相流理论与有限单元法,本文分析了边界透气性在降雨入渗过程中对稳定入渗强度、土体孔隙气压力、湿润锋和饱和度垂直分布等的影响,可以得出以下结论。稳定降雨入渗强度与边界透气性的关系呈指数分布,函数拟合关系为y=0.0987lnx+1.7329,并且拟合度良好,随边界透气性的增大稳定入渗强度也随之增大,边界透气性较小时对稳定入渗强度的影响较大。边界透气性较小时孔隙气压力明显较高,入渗强度较低,土体湿润锋下降缓慢。由此,基于水气二相流理论的降雨入渗计算需考虑渗流边界的透气性,以期达到更精准的渗流模拟过程。
[1] 胡 冉,陈益峰,周创兵.降雨入渗过程中土质边坡的固-液-气三相耦合分析[J].中国科学:技术科学,2011,41(11):1469-1482.
[2] 林兴旺,简文彬,董岩松,等.降雨条件下某排土边坡的渗流场及稳定性时变分析[J].水利与建筑工程学报,2015,13(1):36-41.
[3] 荆周宝,刘保健,解新妍,等.考虑流固耦合的降雨入渗过程对非饱和土边坡的影响研究[J].水利与建筑工程学报,2015,13(6):165-171.
[4] 孙冬梅,朱岳明,张明进,等.考虑气相影响的降雨入渗过程分析研究[J].岩土力学,2008,29(9):2307-2313.
[5] 张 杰,韩同春,豆红强,等.探讨变雨强条件下的入渗过程及影响因素[J].岩土力学,2014,35(S1):451-456.
[6] 朱元骏,邵明安.含砾石土壤降雨入渗过程模拟[J].水科学进展,2010,21(6):779-787.
[7] 吴良骥, Bloomaburg G L. 饱和一非饱和区中渗流问题的数值模型[J].水利水运科学研究,1985(2):1-12.
[8] 朱岳明,龚道勇.三维饱和非饱和渗流场求解及其逸出面边界条件处理[J].水科学进展,2003,14(1):67-71.
[9] Marinoschi G. A free boundary problem describing the saturated-unsaturated flow in a porous medium[J]. Abstract and Applied Analysis, 2004(9):729-755.
[10] 李援农,林性粹.均质土壤积水入渗的气阻变化规律及其影响[J].水土保持学报,1997,3(3):89-93.
[11] 张 华,吴争光.封闭气泡对一维积水入渗影响的试验研究[J].岩土力学,2009,30(S2):132-137.
[12] Borsi I, Farina A, Primicerio M. A rain water infiltration model with unilateral boundary condition: qualitative analysis and numerical simulations[J]. Mathematical Methods in the Applied Sciences, 2006,29(17):2047-2077.
[13] 刘 刚,童富果,习念念,等.通气和封气条件下降雨对粘性土入渗速率、含水率及孔隙压力的影响试验[J].水电能源科学,2015,33(12):19-21.
[14] Tong F, Niemi A, Yang Z, et al. A numerical model of tracer transport in a non-isothermal two-phase flow system for CO2geological storage characterization[J]. Transport in Porous Media, 2013,98(1):173-192.
[15] Carrick S, Buchan G, Almond P, et al. Atypical early-time infiltration into a structured soil near field capacity: The dynamic interplay between sorptivity, hydrophobicity, and air encapsulation[J]. Geoderma, 2011,160(3/4):579-589.
[16] 付建新,宋卫东,杜建华.考虑二维降雨入渗的非饱和土边坡瞬态体积含水率分析[J].工程科学学报,2015,37(4):407-413.
The Impact of Different Gas Boundary Condition on Rainfall Infiltration
HAO Shuang, TONG Fuguo, LIU Gang, XUE Song
(CollegeofHydraulic&EnvironmentalEngineering,ChinaThreeGorgesUniversity,Yichang,Hubei443002,China)
Based on the theory of two-phase (water and gas) flow, this study presents results from the finite-element analysis of soil rainfall infiltration on different gas permeable conditions, and analyzes the influence of gas boundary permeability on the stable infiltration intensity, pore gas pressure and soil saturation distribution. Gas permeable boundary is one of the essential control conditions in the seepage simulation. A quantitative analysis has been proposed to figure out the impacts of gas permeable boundary on the process of rainfall infiltration, while a majority of conventional studies focus on qualitative research. The simulation results indicate that there is a highly relevant relationship between stable infiltration intensity and gas permeability on the boundary. The stable infiltration intensity is sensitive when the gas boundary permeability is at a low stage, and as the gas boundary permeability going up the sensibility of stable infiltration intensity is declined. The equation between stable infiltration intensity and gas boundary permeability is regressed to be logarithmic. Besides, during the process of rainfall infiltration the pressure of pore gas soars up and the movement of wetting front slows down with lower gas boundary permeability.
rainfall infiltration; gas boundary condition; two-phase flow of water and gas; infiltration intensity
10.3969/j.issn.1672-1144.2017.02.010
2016-12-28
2017-01-23
国家自然科学基金项目(51279090, 51679129)
郝 霜(1991—),女,内蒙古呼和浩特人,硕士研究生,研究方向为水工结构。E-mail:shuanghao@ctgu.edu.cn
童富果(1972—),男,湖北宜昌人,教授,博导,主要从事水工结构和岩土工程领域的多场耦合(THMC)问题及其数值方法研究工作。E-mail:tfg@ctgu.edu.cn
P641.2
A
1672—1144(2017)02—0055—05

