既有预应力混凝土简支梁预应力损失的有限元模拟研究

高 杰，黄 颖

(福建船政交通职业学院， 福建 福州 350007)

既有预应力混凝土简支梁预应力损失的有限元模拟研究

高 杰，黄 颖

(福建船政交通职业学院， 福建 福州 350007)

应用大型有限元分析软件ANSYS建立一根已经服役20年的既有预应力混凝土后张板梁单元的有限元模型，采用弹簧单元Combin 39模拟预应力钢筋和混凝土间的粘结滑移效应，通过调整该弹簧单元的刚度来控制预应力钢筋和混凝土间的粘结程度。在模型中同时考虑了预应力瞬时损失和长期损失，较为精确的对既有预应力混凝土结构进行有限元模拟。对该模型进行构件的弹塑性变形、混凝土开裂到极限承载力破坏的全过程分析，得到的结果与试验结果有较高的吻合度，进一步表明该模拟方法的合理性和有效性，为预应力结构精细化建模分析提供一定的参考。

既有预应力简支梁；有限元分析；粘结滑移；预应力损失

应用有限元分析软件对预应力混凝土结构进行精细化分析模拟，有效的对既有预应力混凝土结构的预应力损失进行评估一直是近些年研究的热点和难点，近三十年来随着计算机技术的发展,预应力混凝土结构非线性有限元分析得到了广泛深入的研究。对预应力结构进行有限元分析开始于20世纪80年代，Kang Y J等[1]和Van Greunen J等[2]分别对预应力混凝土框架结构进行了非线性有限元分析研究，考虑了有几何非线性以及预应力损失中混凝土收缩徐变、钢筋松弛的时变效应，进行了构件受力全过程分析Kawakami等[3]利用AD1NA软件建立了混凝土梁和柱的非线性有限元模型，模型采用九节点等参数平面应力单元来模拟混凝土，三结点杆单元来模拟钢筋，考虑了材料的非线性和几何非线性。杨铮[4]利用ANSYS软件建立了预应力框架结构的有限元模型，考虑了钢筋和混凝土的联合作用，采用“涂抹式”裂缝模型进行非线性计算分析。Meng Chan Zhou等[5]利用MIDAS/Civil建立一根32 m长的简支箱型预应力混凝土梁有限元模型，主要进行施工阶段监控分析。高杰等[6]为了获得预应力简支梁三个代表性截面预应力损失度与挠度增量之间的数学模型，建立了精细化预应力混凝土简支梁有限元模型。

本文结合一根已经服役20年的预应力混凝土简支板梁单元试验分析结果[7]，建立ANSYS精细化三维有限元分析模型，在有限元模型基础上，考虑预应力钢筋各类瞬时损失和长期损失[7]，将建立的模型进行加载，获得从弹性变形、裂缝发展到极限破坏的全过程响应。

1 预应力简支梁三维有限元模型建立

1.1 单元模型建立

混凝土单元模型采用等参数的八节点六面体单元，用于考虑三维的钢筋混凝土，可以考虑混凝土开裂和压碎，如图1(a)所示，具体计算公式参见文献[8]。普通钢筋单元可以采用和混凝土相同的单元，考虑到钢筋常呈细长形，其抗剪强度及抗弯强度可以忽略，通常采用三节点一维等参单元，与混凝土单元的变形协调统一，单元模型如图1(b)。

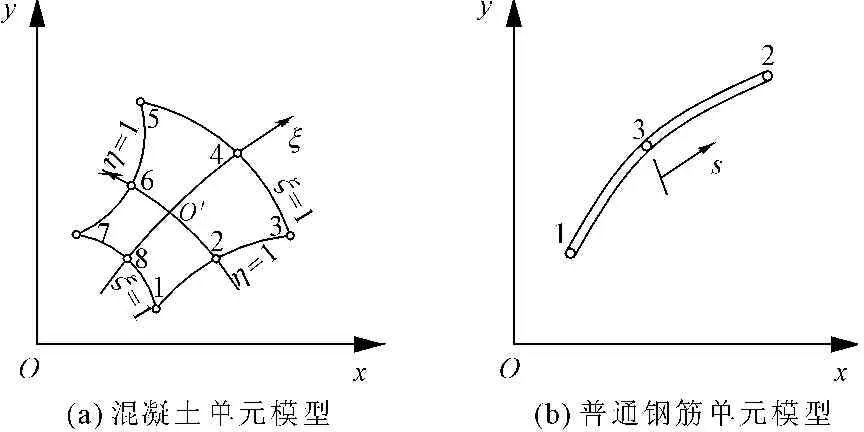
图1 单元模型

预应力钢筋单元模型采用文献[6]中提出的单元，其变形包括预应力钢筋单元所在的混凝土单元沿着曲线孔道壁的变形和预应力筋与混凝土孔道壁的相对位移。本文建立的粘结滑移单元可以用来模拟钢筋和混凝土之间的粘结滑移以及裂缝两侧骨料的咬合作用，采用由相互正交的2根弹簧(平面问题)或3根弹簧(空间问题)组成的弹簧单元[9]，如图2所示，平行预应力钢筋方向的弹簧模拟预应力钢筋与混凝土的粘结滑移，其它方向弹簧模拟混凝土对预应力钢筋的挤压。

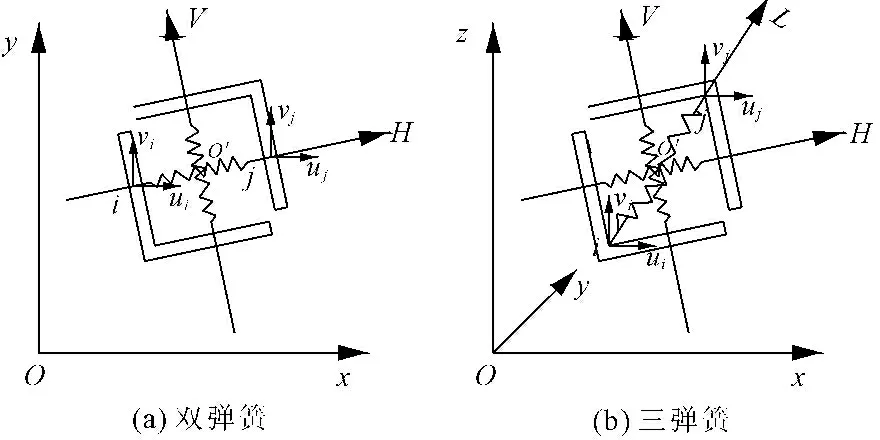
图2 弹簧联结单元模型

该模型形式简单，力学概念明确，便于应用，弹簧具有刚度，但无实际几何尺寸，因此可以置于任何需联结之处。

1.2 材料本构关系

目前在混凝土结构非线性分析中主要有两种形式，即全量形式和增量形式[8]，全量形式采用割线模量，关系式比较简单，全量形式仅适用按比例一次加载；增量形式采用应力增量与应变增量的形式，材料本构矩阵将两者联系起来，利用切线模量，应力-应变关系与加载路径有关。本文的分析采用混凝土的本构模型与文献[10]中用到的一致，混凝土应力-应变关系如图3(a)所示；钢筋的应力-应变关系[8,10]如图3(b)所示；为了提高计算效率，将原本构关系中的曲线用近似的分段折线来代替，预应力筋的应力-应变关系由五个折线段表示[6]，如图3(c)所示。

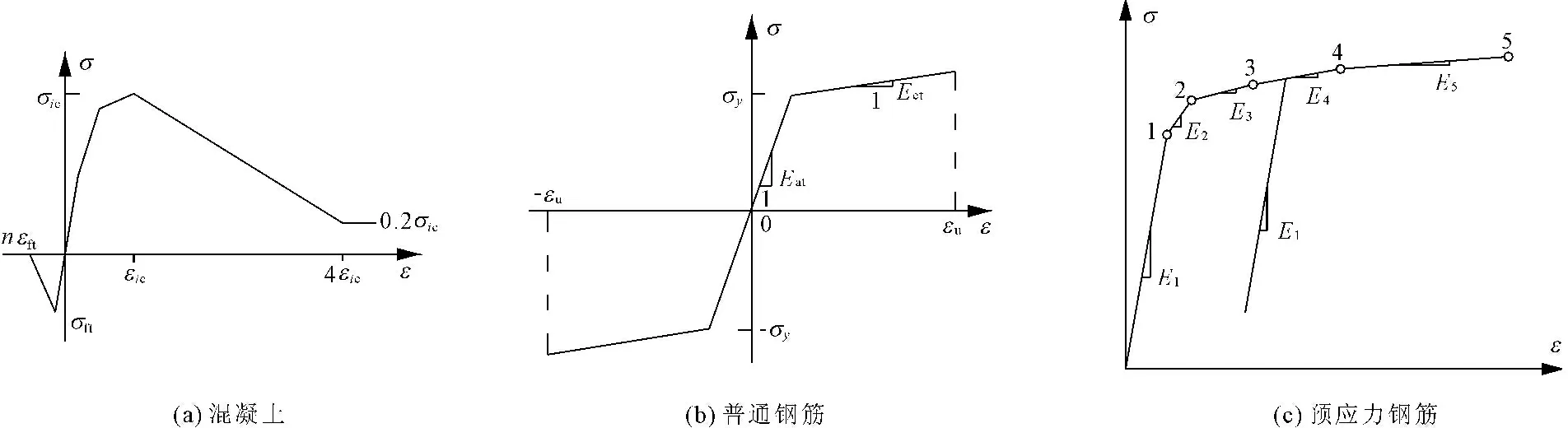
图3 单元应力-应变关系

1.3 有限元软件中单元选择

在ANSYS中，采用Solid 65模拟混凝土材料，Solid 65单元在普通8节点三维等参单元的基础上增加了针对混凝土材料的参数和整体式钢筋模型[9]；预应力钢筋单元采用常用的Link 8单元[9]。

预应力钢筋和混凝土的接触面之间的相对移动有法向、纵向切向和横向切向三个方向，为全面考虑连接面上的相互作用，在两者连接面上在每一对对应节点之间均分别建立三个非线性弹簧Combin 39单元来模拟钢筋与混凝土之间三个方向的相互作用，弹簧的模型采用三弹簧联接模型如图2(b)所示。

2 预应力损失的有限元模拟

2.1 张拉摩擦损失的计算分析与有限元模拟

因为预应力钢筋的瞬时损失与时间无关，所以在有限元模拟中进行简化分析，利用规范[11]推导的预应力摩擦损失力Nl1，将其一分为二，分别作用于单元的两端节点，作为等效摩擦力。

2.2 收缩与徐变的计算分析与有限元模拟

在结构施工和使用过程中，混凝土的收缩和徐变对结构的变形和内力均有巨大的影响，目前，主要采用的徐变计算理论是以徐变与应力的线性关系为依据的初应变法[12]。

2.2.1 混凝土徐变应变计算

将时间轴上各个时刻t0、t1、…tn、tn+1作用的应力增量定义为Δσ0、Δσ1、…、Δσn、Δσn+1、…。考虑在tn时刻，在Δtn+1(tn～tn+1)时间内的情况，单元内任意一点的应力为：

(1)

在Δtn+1(tn～tn+1)时间内，不考虑结构的应力和材料常数变化的影响，则徐变增量为：

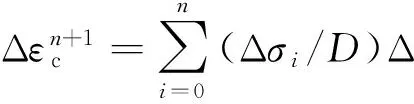
(2)

式中：D为混凝土的刚度矩阵；Δφ(tj，ti)为加载龄期为ti，计算考虑龄期为ti时的混凝土徐变系数。

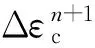
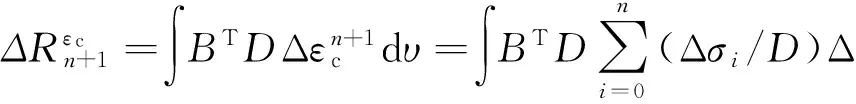
(3)

Δσi=D(Δεi-Δε0i)

(4)

其中：Δεi为结点上一时刻的应变增量(包括由温度变化、施工误差、收缩徐变等初应变产生)；BT为应变矩阵。

(5)

其中：

ΔRi2=-∫BTDΔε0idυ

式中：ΔRi1为由结点位移增量引起的杆端力增量；ΔRi2为由Δε0i引起的固端力增量。

将式(5)代入式(3)可得：

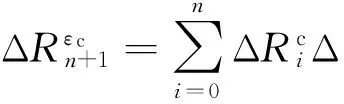
(6)

利用桥梁规范[11]附录F中的方法计算徐变系数：

Δφ(tj,ti)=φ0βc(tj-ti)

(7)

将公式(7)代入式(6)得到：

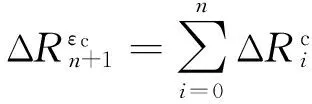
(8)

2.2.2 混凝土收缩应变计算

混凝土的收缩应变对结构的影响也可以作为初应变问题进行计算，收缩应变通常采用指数函数曲线[14]：

εs(t)=εs(∞)(1-e-pt)

(9)

其中：εs(∞)为收缩应变极限；P为收缩应变增长系数。

各单元混凝土的龄期不同，因此收缩计算的起点也就不同，设混凝土的硬化时间为τ0，则：

(10)

则收缩引起的结点荷载为：

(11)

对于等截面杆件单元，其增量的绝对值为：

(12)

则单元收缩固端力向量为：

(13)

则由收缩引起的单元等效结点荷载增量为：

(14)

2.2.3 收缩与徐变损失的有限元模拟

利用ANSYS对混凝土徐变和收缩采用时程分析法[13]，分析时对于时间轴的确定及时步的划分，收缩徐变一般遵循指数函数的规律，因此每个阶段的时间步长可以依据对数函数公式来选取：

Tsm=(lnTe-lnTs)/n

(15)

lnTi+1=lnTi+Tsm

(16)

其中：Tsm为时间步长(对数形式)；Te为收缩徐变计算终了时刻，d；Ts为成桥时刻，d；n为运营期间计算时间步数；Ti+1、Ti分别为第i和i+1步长对应的时刻(i=0,1,2,3,…n)。

其中在时步的每一次循环中包括7个主要步骤，具体方法详见文献[13]，这样即用有限元的方法实现了混凝土的收缩徐变计算。

2.3 钢筋松弛的计算分析与有限元模拟

预应力钢筋在持续应力作用下，应力就会随着时间的变化而降低，这种降低的应力即为预应力钢筋松弛引起的应力损失[15]。

Magura[16]提出预应力钢筋的松弛公式：

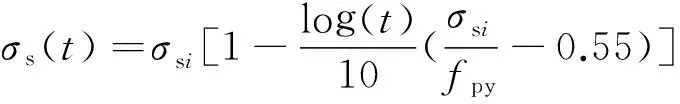
σsi≥0.55fpy

(17)

式中：σs为经t小时后剩余的应力；σsi为初始应力；fpy为屈服强度；t为所经历的时间，该公式只适用于应力为常数的情况；本文对预应力钢筋松弛的分析采用kang提出的改进办法[1]，将松弛应力看做残余应力，采用下列公式可以转化为节点力。对于有粘结预应力钢筋：

(18)

式中：Δσprlx为某段时间内的应力松弛量。

预应力钢筋松弛有限元模拟采用与收缩和徐变相同的时间步长，其他的瞬时损失是固定施加在杆件两端，每一步的时间步计算只要根据混凝土收缩徐变损失及钢筋摩擦损失推算出该时间步的虚拟初始应力，由公式(17)计算出到下一个时间步预应力钢筋应力松弛应力，再根据公式(18)转化为作用在杆单元两端的节点力，通过这种过程实现预应力钢筋松弛的有限元模拟。

3 有限元模拟与试验结果对比分析

有限元建立的模型样本取自一根连续梁的一跨切割单元，模型的几何和材料参数详见文献[7],计算模型见图5(a)。试验模型的混凝土为一般养护,张拉摩擦损失的计算中圆心角按照设计图纸实际取值，取预应力钢筋与管道壁的摩擦系数μ为0.15，管道每米局部偏差对摩擦的影响系数k取0.0015 rad/m。如图4所示，该梁单元中间预应力钢筋为N13，两侧的预应力钢筋为N16，混凝土加载龄期取28 d，收缩徐变终了时刻取成桥时刻后的20 a(7 300 d)，以2 a作为时间步，则运营期间的计算时间步数为9，有限元具体计算步骤如下：

图4 单元构件横断面(单位：cm)

(1) 计算过程首先模拟预应力钢筋张拉与锚固滑移，此时采用的是无粘结预应力钢筋单元，在预应力筋左端加N=565 kN张力,然后在反方向加N的6%，模拟锚固滑移损失。张拉完成后的梁体的变形图如图5(b)所示，此时梁体在重力和预应力作用下，起拱为1.946 mm。

图5 有限元模型受力变形示意图

(2) 张拉完成后，对预应力钢筋进行灌浆，此时将预应力钢筋换成粘结单元，加入粘结滑移单元进行模拟。

(3) 按照2.2、2.3所述方法模拟钢筋松弛、混凝土的收缩与徐变，在有限元分析中，定义混凝土加载龄期为28 d，以2 a作为一个时间步长，总时长为20 a，则计算步数Tsm=10。

(4) 在该已服役20 a的预应力混凝土梁的有限元模型基础上，按照试验工况进行加载，获得其最终变形形态，如图5(c)所示，获得1/4、1/2、3/4三个截面荷载与挠度曲线，如图6所示；整个模拟过程预应力钢筋的应力曲线如图7所示。

图6 各截面荷载-挠度曲线

4 结 语

本文利用有限元软件ANSYS建立既有预应力混凝土板梁单元三维有限元模型，采用弹簧单元模拟预应力钢筋和混凝土之间的粘结滑移，通过调整该弹簧单元的刚度有效的模拟了粘结的有效程度，同时将预应力瞬时损失和长期损失影响加入有限元模型中，对该模型进行构件受力的全过程分析，并将数值分析结果和试验结果进行对比分析，得出如下结论：

图7 预应力钢筋应力分布

(1) 从梁单元三个关键截面荷载-挠度曲线可以看出，有限元计算值和试验值在梁体弹性受力阶段基本吻合，进入塑性阶段后，在相同外荷载情况下，有限元计算得到的梁体挠度要略微小于试验值，这可能是由于试验采用的板梁单元在切割过程中梁体损伤造成的。

(2) 预应力钢筋张拉锚固后应力变化不大，锚固端预应力应力损失在14%左右，而通过钢筋松弛、混凝土收缩和徐变的迭代计算后，应力损失出现较大波动，中间N13预应力钢筋的预应力损失为23%，两侧N16预应力钢筋的预应力损失为33%。

(3) 从有限元计算值和试验值的对比分析可知，两者具有较高的吻合度，验证了有限元模型的有效性，进一步说明本文提出的对既有预应力混凝土结构有限元模拟分析方法的合理性和可应用性，为既有预应力混凝土结构现存有效预应力的分析提供一定的参考。

[1] Kang Y J, Scordelis A C. Nonlinear analysis of prestressed concrete frames[J]. Journal of the Structural Division, ASCE, 1980,106(ST2):445-462.

[2] Greunen J V, Scordelis A C. Nonlinear analysis of prestressed concrete slabs[J]. Journal of Structural Engineering, ASCE, 1983,109(7):1742-1760.

[3] Kawakami M, Ito T. Nonlinear finite element analysis of prestressed concrete members usingAD1NA[J]. Computers & Structures, 2003,81(8/11):727-73.

[4] 杨 铮.预应力混凝土结构的三维有限元分析与研究[D].杭州：浙江大学，2005.

[5] Zhou M C, Liu Q Y, Su J. The nonlinear finite element analysis of prestressed concrete box girder[J]. Applied Mechanics and Materials, 2013,361/363:1384-1388.

[6] 高 杰，黄 颖.既有预应力结构现存预应力数学模型研究[J].水利与建筑工程学报，2015，13(6)：183-187.

[7] 黄 颖，房贞政.已服役20年预应力结构现存预应力的试验研究[J].哈尔滨工程大学学报，2014，35(10)：1201-1205.

[8] 江见鲸，陆新征编著.混凝土结构有限元分析[M].2版.北京：清华大学出版社，2013.

[9] 王新敏编著.ANSYS工程结构数值分析[M].北京：人民交通出版社，2013.

[10] Darwin D, Pecknold D A. Analysis of RC shear panels under cyclic loading[J]. Journal of the Structural Division, ASCE, 1976,102(2):355-369.

[11] 中华人民共和国交通部.公路钢筋混凝土及预应力混凝土桥涵设计规范：JTG D62-2004[S].北京：人民交通出版社，2004．

[12] 朱伯芳.有限单元法原理及应用[M].北京:水利电力出版社，1979.

[13] 黄 颖，高 杰.预应力混凝土结构收缩与徐变损失的计算分析与有限元模拟研究[J].四川理工学院学报(自然科学版)，2016，29(3)：75-80.

[14] Neville A M, Dilger W H, Brooks J J. Creep of Plain and Structural Concrete[M]. London: Construction Press, 1983.

[15] 房贞政编著.预应力结构理论与应用[M].2版.北京：中国建筑工业出版社，2014.

[16] Magura D D, Sozen M A, Siess C P. A Study of Stress Relaxation in Prestressing Reinforcement[J]. PCI Journal, 1964,9(2):13-57.

Finite Element Simulation of Prestress Loss of a Prestressed Concrete Simply Supported Beam

GAO Jie, HUANG Ying

(FujianChuanzhengCommunicationsCollege,Fuzhou,Fujian350007,China)

A finite element simulation model of a post tensioned prestressed concrete beam which has served 20 years was developed by ANSYS software. The spring unit Combin 39 was adopted to simulate the bond slip effect between prestressed steel and concrete, through adjusting the spring element stiffness to control the degree of bonding between prestressed steel and concrete. The model considers instantaneous loss and the long-term loss, which makes the finite element simulation of prestressed concrete structure more accurate. The procedure can predict the responses of post-tensioned concrete structures throughout the service load history, such as elastic and plastic deformation, cracking and damage patterns. Numerical examples of beams model are presented. The comparison of computed results with experimental ones shows good agreement, demonstrating the efficiency of the proposed model, which provided certain reference for precise modeling of prestressed structure.

extant pre-stressed simply-supported beam; finite element analysis; bonding slip; prestress loss

10.3969/j.issn.1672-1144.2017.02.012

2016-11-27

2017-01-10

国家自然科学青年基金项目(51108092)；福建省教育厅科技项目(JA15664)

高 杰(1966—)，男，福建平潭人，副教授，主要从事桥梁结构耐久性能方面的工作。E-mail: 52845185@qq.com

TU311.3

A

1672—1144(2017)02—0065—06