钛合金典型连接结构裂纹扩展特性分析*
肖 山,毕金英,孙彦鹏,刘书田,刘 杨
(1. 航空工业沈阳飞机设计研究所,沈阳 110035;2. 大连理工大学工业装备结构分析国家重点实验室,大连 116024)
钛合金由于具有比强度高、耐久性强、抗腐蚀、可焊接等优异的综合性能,在航空航天工业领域中获得了广泛应用。例如,美国F35战斗机钛合金构件利用率达到20%,F22战斗机钛合金利用率甚至达到40%以上[1]。但钛合金存在损伤后裂纹扩展寿命较短的问题,难以保证结构的使用安全[1]。因此,研究新型钛合金材料、成形工艺和发展新的提高钛合金结构损伤容限特性的设计方法成为目前的研究热点。
通过扩散连接[2]的层合方式来提高钛合金的断裂韧性、降低裂纹扩展速率以及延长裂纹扩展路径,已成为改善钛合金材料和结构损伤容限特性的重要研究方向。
为了适应航空领域越来越高的损伤容限设计要求,近年来,在钛合金扩散连接层合方式等方面已经开展了较为丰富的研究工作,取得了一系列较为重要的研究成果[3-7]。
周克印等[3]针对扩散连接制造的钛合金多层板[4-5]连接界面(DB界面)对裂纹的扩展抑制作用进行了研究,通过钛合金TC4扩散连接后与其母板中裂纹扩展的比较发现,DB界面可以引起裂纹扩展方向的改变,能够改善疲劳断裂性能。
钛合金中预置非焊合区会降低其一定的承载能力,然而非焊合区的存在也可能阻碍裂纹的扩展,改善结构的损伤容限特性。贺小帆等[6]通过试验的手段对DB层中预置非焊合区的元件级含孔扩散连接钛合金层合板进行了疲劳裂纹扩展研究,研究表明非焊合区能够改变钛合金层合板的疲劳裂纹扩展路径,延长裂纹的扩展寿命。为实现对含非焊合区层合结构的优化设计,需建立与其相应的有限元分析手段,文献[7]对元件级含孔扩散连接钛合金层合板疲劳裂纹扩展特性开展了数值模拟方法的研究,建立了一种适用该结构特性的有限元分析方法,并通过试验研究验证了分析方法的有效性。合理地布置非焊合区,抑制裂纹的扩展,是提高钛合金疲劳裂纹扩展寿命、增强结构使用安全的有效方法,在框、梁缘条与接头耳片等易萌生裂纹的飞机结构中具有重要的应用前景。
然而,新结构形式的工程应用必然伴随着积木式的系统验证,以往的研究工作只针对元件级的含非焊合区钛合金层合板开展了裂纹扩展特性研究,尚无对非焊合区在飞机典型结构中的应用开展研究。本文选取钛合金典型连接结构,以孔边在受螺栓挤压情况下的接头耳片为分析对象,研究含非焊合区连接结构的裂纹扩展规律以及非焊合区对裂纹扩展寿命的增强机理。

图1 分析模型(mm)Fig.1 Analysis model
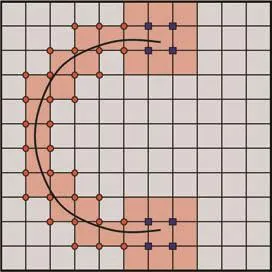
图2 扩展有限元示意图Fig.2 Extended finite element graph
1 研究对象和求解方法
1.1 研究对象
本文基于Abaqus采用XFEM方法分别对钛合金传统机加典型接头耳片与含预置非焊合区的典型层合接头耳片结构进行疲劳裂纹扩展特性分析。有限元建模时设置初始裂纹,重点研究疲劳裂纹在钛合金层合板内的扩展规律,不考虑结构的裂纹萌生寿命。两类试件外廓尺寸相同,长、宽和厚度分别为L=160mm、W=60mm、T=20mm,中心含直径为φ=30mm的螺栓孔。其中,机加试件为单层;含非焊合区试件由5层钛合金平板扩散连接而成,厚度分布为2+4+8+4+2(mm),在螺栓孔周围的DB层内预置φ=40mm的圆形非焊合区;两类试件孔边预设r=0.5mm的1/4圆初始角裂纹面,如图1所示。加载方式为轴向拉-拉,载荷为正弦等幅谱,应力比R=0.1。层合板为钛合金TC4,da/dN=C(ΔK)m中的C=5.25×10-8,m=2.85和断裂韧性KC=78.3(MPa·m1/2),材料常数弹性模量E为110GPa,极限强度σb为913MPa,能量释放率Gc为 55.7J/m2,泊松比ν为0.34.[8]。本文采用能量释放率准则进行分析,疲劳裂纹扩展速率的预测采用 Paris公式:da/dN=C'(ΔG)m',C'、m'和GC(材料极限能量释放率),采用文献[9]中公式转换得到C'=3.2×10-5、m'=1.43和GC=55.7N/mm。
试验验证在一个标准大气压、室温下进行,试验机为MTS电液伺服疲劳试验机。利用电火花方法在试验件的孔边一侧预设宽0.2mm、半径r=0.5mm的1/4圆初始角裂纹面。耳片的端部夹持,在螺栓孔处通过螺栓施加疲劳载荷,加载方式为轴向拉-拉,载荷为正弦等幅谱,应力比R=0.1。
1.2 求解方法
在Abaqus/Standard中,基于XFEM框架下的移动裂纹建模方法-线弹性断裂力学准则(LEFM)进行数值模拟,分析采用隐式非线性有限元程序Standard。其主要求解步骤如下[10]:
(1)采用扩展有限元方法求解应力和位移场。XFEM[10-11]是一种处理力学不连续问题的数值方法,在裂纹附近的网格节点增加附加自由度和增强函数来表达裂纹面上位移的强不连续和裂尖的应力奇异。图2给出了二维情况下需要补充附加自由度的单元节点。扩展有限元的位移函数可以表示为:

其中,K为全部单元的节点,Kr为被裂纹面贯穿的单元节点(图2中的圆形节点),KΛ为裂尖所在的单元节点,uI为单元节点的位移,aI、bα I分别为裂纹贯穿单元与裂尖单元节点的附加自由度。式(1)中位移跳跃函数H(ψ(x,t))的定义为:

其中,φ(x,t)为裂纹前沿水平集函数,ψ(x,t)为裂纹面水平集函数,其定义为:

其中,分别为裂纹面的单位法向矢量和裂尖的单位切向矢量,xr为裂纹面延长面上点的坐标。r(t)表示裂纹面的延长面,x*是裂尖的坐标。公式(1)中奇异增强函数Fα(x)为:
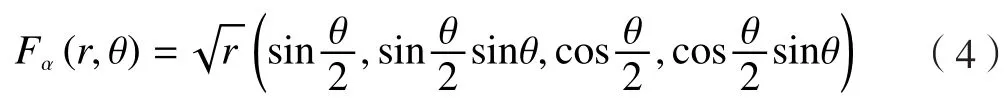
式中,
(2)计算能量释放率。根据XFEM方法计算获得裂纹尖端应力场,采用VCCT方法计算裂纹尖端处的应变能释放率。
(3)根据能量释放率准则作为扩展准则,当最大应变能释放率GM大于材料疲劳扩展的阈值Gth时,疲劳裂纹开始扩展。本文疲劳裂纹扩展的阈值取Abaqus中默认的Gth=0.01GC,裂纹扩展方向判据采用最大切应力准则。
Abaqus中XFEM的位移插值列式中不包含描述裂纹尖端奇异性的增强函数。裂纹扩展时,裂尖以单元边界为起止点而不会停留在单元内部,因此在计算裂纹面前缘扩展时,不是使整个裂纹面前缘都向前扩展,而是计算裂纹穿过裂纹面前缘各单元所需要的循环次数Nj,取min(Nj)作为当前分析扩展的次数N,并使min(Nj)所在的单元扩展。如果几个Nj都接近min(Nj)则让几个单元同时扩展。扩展时,以单元为单位进行逐步扩展,每次扩展一步以后重新计算下一步扩展的单元以及相应的循环次数N。
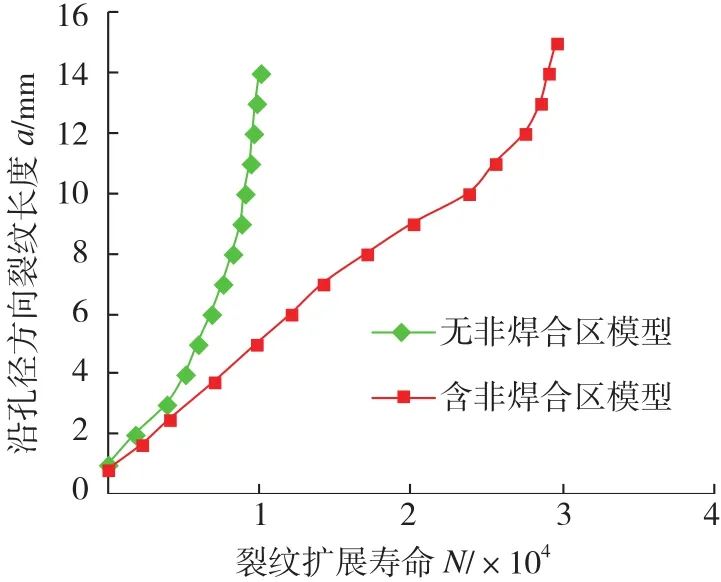
图3 a-N曲线数值分析结果Fig.3 Numerical analysis results of a-N curves
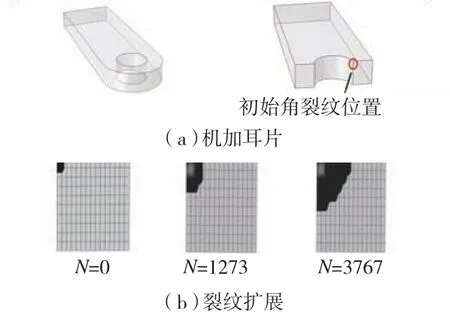
图5 机加耳片裂纹扩展轨迹Fig.5 Crack growth path of traditional lug
2 结果与讨论
在飞机结构服役过程中进行裂纹检测和修理时,通常将沿孔径方向的裂纹扩展规律作为裂纹扩展性能的重要描述参数。从图3中裂纹长度与扩展寿命对比曲线可以看出,相对传统机加试件,层合界面中预置非焊合区使裂纹扩展寿命提高2倍以上,这反映出孔边在受螺栓挤压时,非焊合区对裂纹的扩展有同样的(与元件级典型试件比较)抑制作用[6-7]。两类试件沿孔径方向的da/dN-a对比曲线如图4所示,无非焊合区时,随着裂纹长度的增大,沿孔径方向的裂纹扩展速率急剧增长;而多个非焊合区的设置,改变了裂纹的扩展速率,使裂纹扩展速率显著下降,这表明合理的布置非焊合区对裂纹扩展的抑制作用更明显。
通过两者的裂纹扩展轨迹对比分析看出:机加试件扩展路径单一(图5),裂纹沿耳片厚度和径向同时扩展,直到结构完全失效;然而含非焊合区层合试件裂纹的扩展分为3个扩展阶段(图6):第一阶段,单层内的扩展;第二阶段,临近非焊合区边界的扩展;第三阶段,裂穿非焊合区后的扩展。第一阶段,随着裂纹的增长,裂纹扩展速率急剧增大,当裂纹扩展到非焊合区边界(第二阶段)时,裂纹扩展速率迅速降低,表明非焊合区对裂纹扩展有显著的阻碍作用;当疲劳裂纹面前缘越过非焊合区边界时(第三阶段),裂纹扩展速率又迅速增大,结构剩余强度急剧下降,发生瞬断。
裂纹扩展长度与循环次数a-N曲线对比分析时,以a0=0.5mm作为初始裂纹长度。两类试件的a-N曲线数值与试验对比结果如图7所示,通过数值分析方法得到的裂纹扩展寿命与试验手段测得裂纹扩展寿命基本一致,并且两者的a-N曲线变化趋势相同,这表明XFEM可准确获得机加接头耳片与含预置非焊合区的层合接头耳片结构在受螺栓挤压时的裂纹扩展寿命与扩展规律。
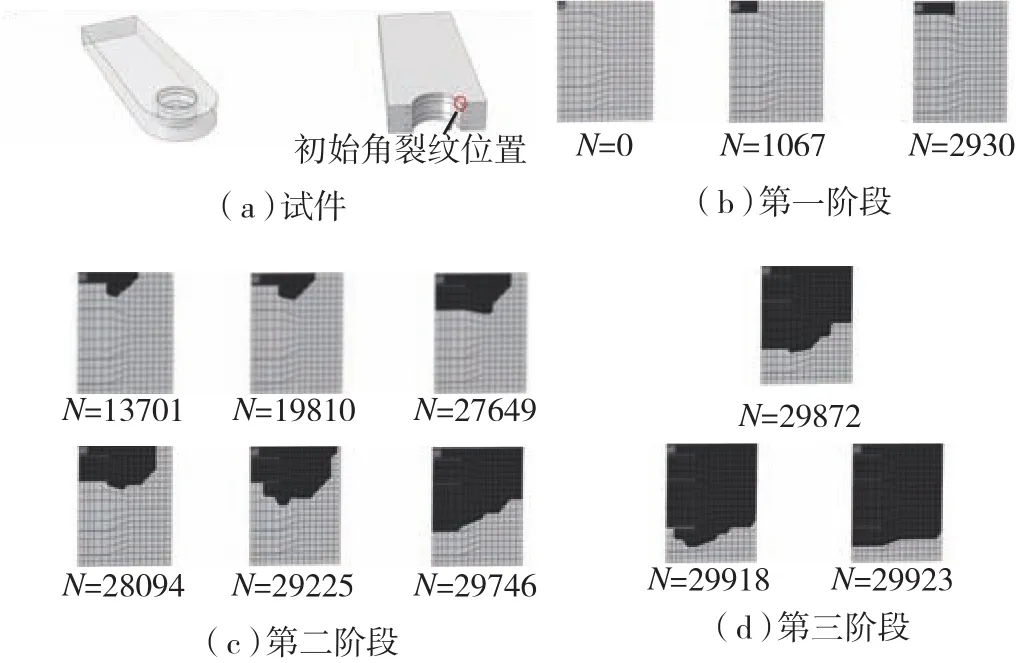
图6 含非焊合区试件裂纹扩展轨迹Fig.6 Crack growth path of diffusion bonded lug with non-welded area

图7 机加试件和含非焊合区试件a-N曲线数值与试验对比Fig.7 Numerical results of a-N curves and the experimental results comparison for traditional lug and diffusion bonded lug with non-welded area
3 结论
对层合耳片在飞机钛合金典型连接结构应用的研究表明:在受螺栓挤压的层合耳片连接界面内预置非焊合区可以显著提高疲劳裂纹的扩展寿命。XFEM数值结果与试验比对分析结果显示:XFEM可准确获得预置非焊合区连接结构在受螺栓挤压时的裂纹扩展规律,是分析该类结构裂纹扩展规律的有效方法。
参 考 文 献
[1]王向明, 刘文珽. 飞机钛合金结构设计与应用[M]. 北京:国防工业出版社, 2010.
WANG Xiangming, LIU Wenting. Titanium alloy structure design and application[M]. Beijing: National Defence Industry Press, 2010.
[2]DERBY B, WALLACH E R. Theoretical model for diffusion bonding[J]. Metal Science, 1982, 16(1): 49-56.
[3]周克印, 徐来, 林兆荣,等. TC4钛板扩散连接后的疲劳断裂特性[J]. 机械强度, 1998, 20(2): 112-115.
ZHOU Keyin, XU Lai, LIN Zhaorong, et al. Fatigue and fracture characteristics of titanium alloy boards bonded by diffusion[J]. Journal of Mechanical Strength, 1998, 20(2): 112 -115.
[4]FRANKIN W L, WAITZ C R. Built-up low-cost advanced titanium structures (BLATS)[C]. 21st Structures, Structural Dynamics, and Materials Conference, Seattle, 1980.
[5]KAIBYSHEV O A. Advanced superplastic forming and diffusion bonding of titanium alloy[J]. Materials Science and Technology, 2006, 22(3):343-348.
[6]贺小帆, 刘彦毛, 刘文珽,等.含孔钛合金扩散连接止焊层合板裂纹扩展特性试验[J]. 航空材料学报, 2011, 31(5): 77-81.
HE Xiaofan, LIU Yanmao, LIU Wenting, et al. Crack growth characteristic for diffusion bonded laminates of titanium-alloy with localized no-welded area[J]. Journal of Aeronautical Materials, 2011, 31(5):77-81.
[7]肖山, 毕金英, 孙彦鹏. 基于扩展有限元的钛合金层合结构裂纹扩展特性研究[J]. 航空制造技术, 2015(17): 86-89.
XIAO Shan, BI Jinying, SUN Yanpeng. XFEM-based analysis for crack growth characteristic of diffusion bonded laminate of titaniumalloy[J]. Aeronautical Manufacturing Technology, 2015(17): 86-89.
[8]中国航空材料手册编辑委员会. 中国航空材料手册[M]. 北京:中国标准出版社, 2001.
China Aeronautical Materials Handbook Editorial Committee. China aeronautical materials handbook[M]. Beijing: Standards Press of China, 2001.
[9]MOËS N, DOLBOW J, BELYTSCHKO T. A finite element method for crack growth without remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 46(1): 131-150.
[10]SHI J, CHOPP D, SUKMAR N, et al. Abaqus implementation of extended finite element method using a level set representationfor threedimensional fatigue crack growth and life predictions[J]. Engineering Fracture Mechanics, 2010, 77(14): 2840-2863.
[11]BELYTSCHKO T, BLACK T. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45(5): 601-620.

