毛坯海量点集与CAD数模的自适应快速精确配准方法研究

李 欢，陈志同，屈新河

（1.北京航空航天大学机械工程及自动化学院,北京 100191；2.中航工业昌河飞机工业（集团）有限责任公司，景德镇 333000）

国内航空工业中的复杂锻铸件毛坯普遍采用人工划线的方式来确定加工余量，这种工艺方式严重滞后，其加工周期长且数控化率低，加工质量稳定性差。为去除这种手工划线的工艺过程，一般采用数字化配准的方式分配每个面的余量，步骤如下：（1）利用扫描仪器扫描毛坯表面，得到海量点集；（2）利用配准算法对齐毛坯点集和CAD数模，使得点集与数模达到最佳位姿，保证所有加工面都有足够的加工余量，同时满足非加工面余量分配均匀的要求。配准过程主要分为粗配准和精配准两步。粗配准的目的是将导入到系统内的点集在工件坐标系下与CAD数模实现大致对齐，可通过主成分分析（Principal Component Analysis，PCA）法[1]或者“由对应三点求坐标变换”的方法[2]等来实现毛坯点集与CAD数模的粗配准。在此基础上，精配准是为了使得每个数模面上分配的余量符合加工要求。本论文是在粗配准完成的基础上讨论如何快速准确地进行精配准。

在进行精配准时，由于点集与数模面数量太多，同时点集与数模面没有任何关联关系，数据点在寻找数模面上的对应点时需要遍历所有数模面以寻求对应面，导致计算量非常大，大大降低了配准效率，最终严重制约工业生产。

在精确配准毛坯点集与理论数模方面，文献[3]提出的方法是在经过粗配准之后，分别提取CAD数模和精铸件点集中的面特征，然后利用提取出的面特征进行精确配准，这种方法要求毛坯表面光滑，适用于精铸件，对于一般的锻铸件，由于其毛坯表面凹凸不平，很难利用此方法进行精确配准；文献[4]根据点云数据的曲率信息将点云分块，然后与相应的面建立关联关系，这种方法可以有效地建立点云与数模面之间的一一对应关系，提高寻找对应点的效率，但计算点云曲率会降低系统的计算效率，同时由于锻铸件毛坯表面不平整，将直接影响关联效果；文献[5-7]主要针对叶片类等数模面比较少的零件模型的配准定位问题，而锻铸件模型的数模面及相应点集数量都非常多，其计算效率无法满足实际生产的需要。

本文针对航空复杂锻铸件毛坯海量点集与CAD数模快速精确配准的问题，提出一种快速精确配准毛坯点集与CAD数模的自适应方法，即利用配准面提取参与配准的数据点，建立点面之间的对应关系，通过不断选取参与配准的特征面及相应的数据点加入配准，直至各面都很好地满足加工要求。

建立如下数学模型

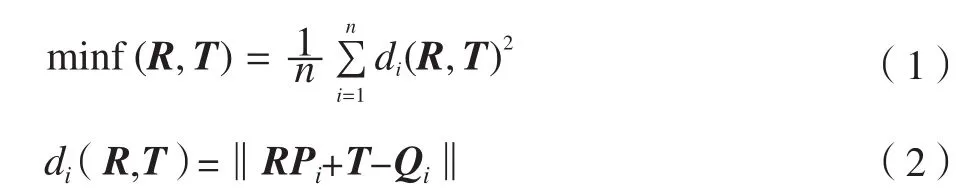
若施加余量进行约束，则上式需满足

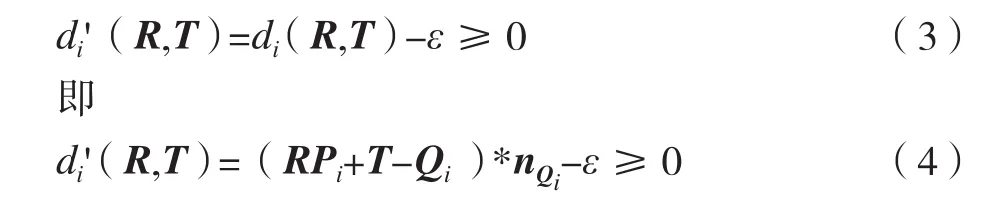
其中，i=0,1,2,3,…,n，Pi为数据点，Qi为CAD数模上的对应点，R为旋转量，T为位移量，nQi为数模上对应点Qi处的外法矢向量，ε为约束余量。（1）式为需要优化的目标函数，（2）式为不加约束的变化量函数，（3）、（4）式为施加余量约束的变化量函数。

本论文的讨论重点是如何快速准确地选取数据点Pi及对应点Qi，对应点Qi通过计算点Pi到对应面的最近点得到，同时介绍了配准面的选取以及快速配准的流程，最后利用实例验证了本文所提方法的高效率以及可靠性。本文的配准算法是基于ICP算法[8]进行的。

1 配准面的选择及分组

1.1 配准面的选择

本文所提出的分批次逐步加入配准面进行迭代配准的方法，要求将配准面进行合理的分组。在分组之前要注意以下两点：

（1）由于参与配准的CAD数模是零件数模，导致很多数模面没有对应的数据点，在配准过程中也不发挥任何作用，为提高配准效率，在进行配准之前需要筛选这些数模面，使其不参与配准。

（2）精配准的主要目的是使所有的加工面都有足够的加工余量，但实际中还要求非加工面部分的对称面上的余量分布均匀，所以在配准过程中也要有非加工面的参与。故需要在配准前区分开加工面和非加工面。

由于在配准过程中，CAD数模始终都是一个，不需要改变，改变的只是不同毛坯的扫描点集，所以可在配准之前标记上述分类，在以后的所有配准中都不需要再进行分类处理。因此，为保证分类完全正确，本文采用手工标记的方式区分配准面和非配准面，以及加工面和非加工面。

如图1所示，以某直升机的尾桨毂壳体为例，标记为绿色的数模面为非配准面，其余为配准面；标记为黄色的数模面为加工面，其余为非加工面。

图1 标记分类数模面Fig.1 Marking classification surfaces

1.2 配准面的分组

在进行精确配准时，为保证配准精度，由六点定位原理可知，从面积较大的面开始，具体分组需遵循以下几点：

（1）配准面中的加工面和非加工面分别按照面积由大到小的顺序进行排序,并在每次配准中按顺序同步加入计算；

（2）由于在实际生产中，要求毛坯非加工面部分的对称面上的余量分布均匀，所以应该对称选取该部分数模面加入到配准中，以达到余量对称分布即分布均匀的目的。对称的数模面面积比较相近或者相等，故本文在每一组的配准面中加工面和非加工面各选2个；

根据以上讨论，将配准面进行分组，分组流程如图2所示。

2 选择配准点的方法

在精确配准时并不需要所有的数据点都加入配准，在每个点云面上只需要提取几个关键点代表该面。

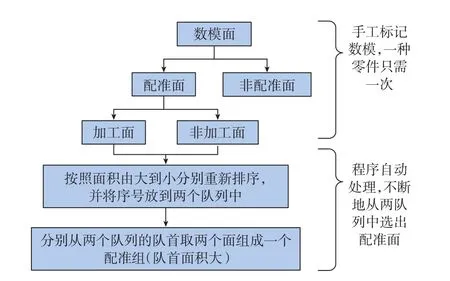
图2 配准面的分组Fig.2 Grouping of registration surfaces

本文采用通过面选取相应数据点的方式来确定配准点，而配准点在点云面上的分布则是通过面上位置点的分布来确定的。所以选取配准点的顺序是：选取配准面→在面上选取位置点→选取配准点，其核心部分是在面上选取位置点。

2.1 在配准面F上选取位置点

为了最大化地表征面F的特征，采用波纹扩散的形式逐步扩散位置点在面F上的位置，波纹线是面F上的曲线，与其外轮廓线相似，以面F的中心点为波源向外部逐渐扩散。在波纹线上均匀选择点作为每次扩散波纹线后的位置点。以下为在第n次扩散后的波纹线上选取位置点的具体步骤：（n=0，1，2，…，N；为保证选取配准点的准确性，避免选到归属于邻面的数据点，当n=N时，扩散后的波纹线要在面外轮廓线的内侧。现使得第n次扩散后的波纹线为面外轮廓线的n/（N+1）倍，即以面的中心点为波源向周围扩散后的波纹线相对于面的外轮廓线缩小的比例为n/（N+1）倍。）

Step 1：当n=0时，波纹线还没开始扩散，此时的波纹线为面的中心点，即第0次扩散后的位置点为面的中心点（由于点面已大致对齐，为提高效率，此时的位置点可直接舍去，不参与配准）；

Step 2：当n≥1时，第n次扩散产生波纹线的方法为：

（1）复制面F，得F'；

（2）将复制面F'按比例n/（N+1）缩小；

（3）将缩小面和原面的中心重合，缩小面的外边界线向原面投影，即可得到相应的波纹线，同时删除复制面；

Step 3：生成波纹线后，在线上均匀选取点作为位置点，点的个数为2n；同时去除不在面上的点，即点位于被裁掉的部分；如图3所示，红色线为波纹线，黑色圆点为有效位置点，红色方点为无效位置点。

2.2 选择配准点

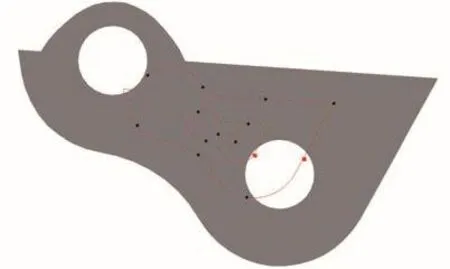
图3 位置点的选取Fig.3 Selection of position points

在配准面F上生成位置点之后，需要根据位置点选择相应的数据点作为配准点，以下为具体步骤：

（1）首先，生成面F的最大包围盒，选择位于盒内的点集作为粗选点集（该步只在首次选取配准点时执行）；

（2）在选出的位置点处生成相应法矢，并以该点为起点，分别向法矢方向及其反方向生成长度为5mm的直线段（考虑到粗配准的精度在±5mm以内，也可以根据不同数模情况手动改变）；

（3）针对每一条长度为10mm的线段，选取距离线段距离小于某一阀值δ的点（δ的值根据点集间的距离l确定，δ≥l）；

（4）选取c中选中的点中距离曲面有向距离数值最小的点为该位置的配准点；如图4所示的3次扩展波纹线后所选择的配准点，蓝色圆点为选择的配准点，其余红色方点为非选中的点集。

图4 配准点的选择Fig.4 Selection of registration points

3 自适应配准方法

以上详细讨论了配准面的选取与分组以及配准点的选取工作，接下来讨论基于ICP算法的自适应配准方法。

自适应配准方法即逐步加入所选配准面进行迭代配准，直至配准结果符合加工要求为止。在配准过程中主要涉及配准面和配准点，用RFace表示配准面集，RPoint表示配准点集。

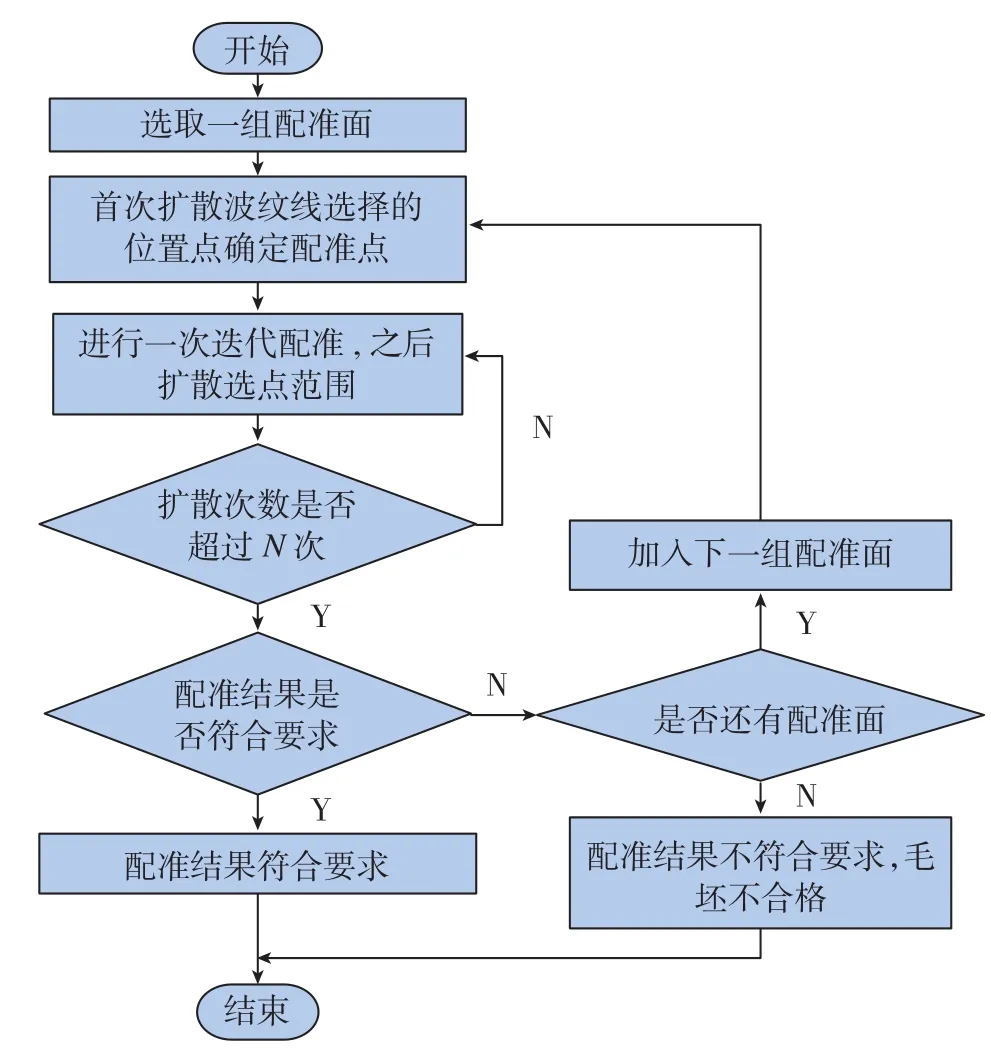
图5 自适应分组配准流程图Fig.5 Flowchart of adaptive and grouping registration

以下为详细步骤：

图5中的一次迭代配准是指将现有的配准点和对应配准面进行反复迭代配准，直至点云位姿的变化量ΔT≤0.01且ΔR≤0.01为止。

Step 1：面积较大的一组配准面加入RFace中；

Step 2：计算新加入配准面对应的配准点：将波纹线第一次扩散后的位置点对应的配准点加入到RPoint中，将RFace和RPoint代入配准算法中进行一次迭代配准；然后扩散新加入配准面对应配准点的选取范围，将新的数据点加入到RPoint中，再次进行一次迭代配准；以此类推，直至扩散N次；

Step 3： 若此时的配准结果符合要求，则结束；否则转向Step 4；

Step 4：若此时已没有未参与配准的配准面，则说明无法利用现有算法合理分配数模各面余量，初步判定毛坯不合格；否则转向Step 5；

Step 5：加入新的一组配准面到RFace中，该组配准面中加工面和非加工面的面积分别是未参与配准的加工面和非加工面中最大的；然后转向Step2。

4 实例验证

以某直升机的尾桨毂壳体为例，进行试验验证。该理论数模的数模面数为1447个，毛坯点集数为103625个，上文的配准面的选择中以该壳体为例进行了配准面的选择，如图1所示。

对于配准点的选择的扩散次数N的取值，不同的零件数模的最优解是不同的，本文根据经验提供一个可行解，令N=3。（N的取值依据：对于某一个特定的零件数模，在前期进行多次试验，N=1,2,3…，选取N的值使得配准效率最高且精度符合加工要求。）

图6 壳体理论数模与毛坯点集配准示意图Fig.6 Registration sketch map of the CAD model and blank point set

图6（a）为精确配准前的状态，图6（b）为按照本文所提方法精确配准之后的状态，经检测，符合加工要求。其中数模中的黄色部分为加工面，其余外表面为非加工面。

表1为对于一个配准点在寻找对应点时所需消耗时间的比较 ；表2为在精确配准上述壳体达到加工要求条件下的配准点、面个数及时间的对比，此处的传统算法是指单纯利用ICP算法进行精确配准；

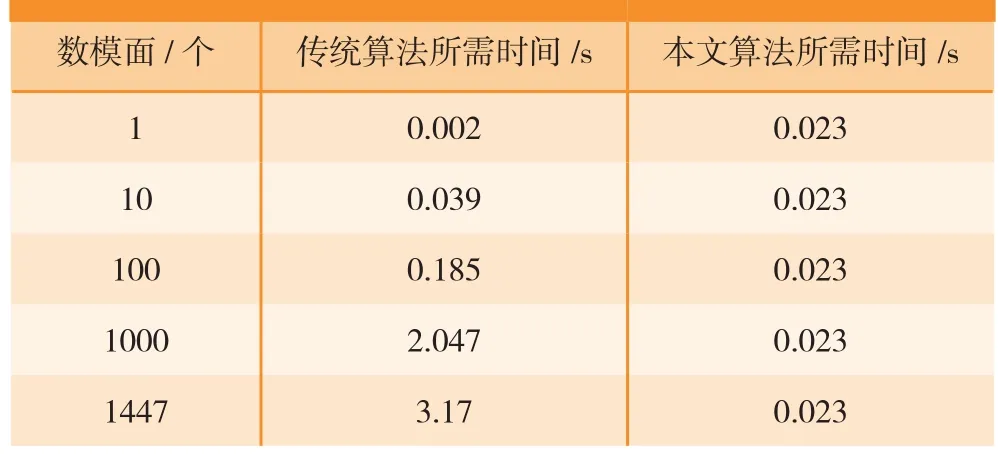
表1 单个点寻找对应点所需时间的对比

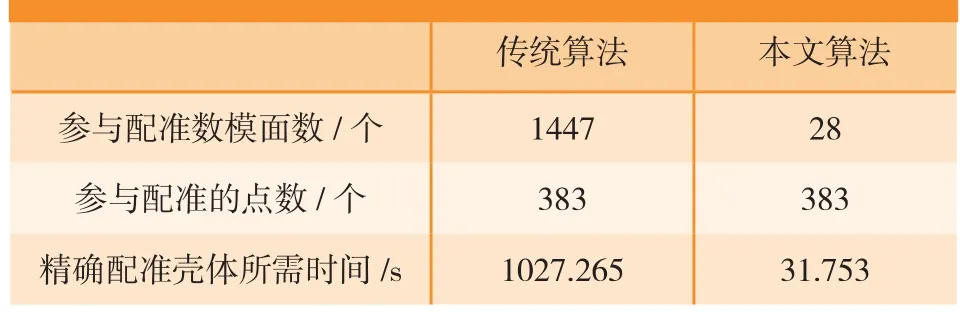
表2 壳体精确配准情况的对比

表1中单个点寻找对应点时，通过计算点到曲面的最短距离来获得，可通过网格法[9-10]来计算点到曲面的最近距离，本文采用方法[10]来计算最近距离；传统的配准计算时点和面没有对应关系，数据点需要计算与每个数模面的最近距离，通过比较找出距离最小的面为该点的对应面，相应的最近点为对应点；当只有一个数模面时，数据点寻找对应点时会直接计算该点与该数模面的最近距离，然后找出相应的最近点为对应点，所以计算时间非常短，只有0.002s，但随着数模面的增加，数据点寻找对应点需要消耗的时间成倍增加。

而本文所提的算法是通过面选择归属于该面的数据点，被选中的配准点都已经有了对应面，求取点到面的对应点时并不受数模面个数的影响，直接计算点到面的最近点即可得到对应点。通过计算可知，此时单个点寻找对应点的平均时间为0.023s。由表1可知，对于航空复杂锻铸件这种由成百上千的数模面构成的CAD数模，本论文所提的算法在寻找对应点方面有着明显的优势。

表2中精确配准壳体点集与数模时， 利用本文所提算法进行精确配准时，结果显示只需要两组配准面（共有28个配准面）参与配准即可使配准精度达到加工要求。为了更直观地比较本论文新算法的高效率，在利用传统算法进行配准时，直接使用本论文新算法配准过程中使用的数据点进行精确配准。

如表2所示，对于航空复杂锻铸件的精确配准，本论文所提算法在配准效率上有非常明显的优势。

5 结论

（1）提出了利用数模面选取参与配准的数据点的方法，其建立点面一一对应关系的时间不受数模面个数的影响，极大地提高了数据点寻找对应点的效率；

（2）在配准前，将数模面进行分类，选取出配准面，同时在配准面中区分开加工面和非加工面，由于一批同类毛坯在生产中只需与同一种CAD数模进行配准，因此这种分类方法适用于工业化生产中，可以提高工业化生产效率；

（3）通过与传统算法的对比，可以看出运用本文提出的方法使得配准效率更高，更具有针对性；

（4）配准点选择过程中的扩散次数N的最优解问题还待后续的工作进一步探讨。中国图像图形学报, 2007, 12(3):517-521.

参考文献

[1] 戴静兰,陈志杨,叶修梓.ICP算法在点云配准中的应用[J].

DAI Jinglan, CHEN Zhiyang,YE Xiuzi. The application of ICP algorithm in point cloud alignment[J]. Journal of Image and Graphics,2007,12(3): 517-521.

[2] 胡栋材,赵歆波,张定华,等. 自适应遗传算法配准三维数字样品模型及其CAD模型[J]. CT理论与应用研究, 2008(2): 8-14.

HU Dongcai, ZHAO Xinbo, ZHANG Dinghua, et al. Registration of Three dimension digital model and CAD model based on the method of adaptive genetic algorithm[J]. Computerized Tomography Theory and Applications, 2008(2): 8-14.

[3] LI Xudong, LI Wei, JIANG Hongzhi, et al. Automatic evaluation of machining allowance of precision castings based on plane features from 3D pointcloud[J]. Computers in Industry, 2013, 64:1129-1137.

[4] 李欢,张丽艳,周良明,等. 面向复杂毛坯小余量加工的层次化快速约束配准算法[J]. 中国机械工程, 2014(11):1524-1529,1561.

LI Huan, ZHANG Liyan, ZHOU Liangming, et al. A hierarchical and fast algorithm of constrained registration for complex blanks with small machining allowance[J]. China Mechanical Engineering, 2014(11):1524-1529,1561.

[5] 严思杰,周云飞,彭芳瑜,等. 大型复杂曲面加工工件定位问题研究[J]. 中国机械工程, 2003,14(9): 737-740．

YAN Sijie, ZHOU Yunfei, PENG Fangyu, et al. Research on localization of the workpieces with large sculptured surfaces[J]. China Mechanical Engineering, 2003, 14(9): 737-740．

[6] 马骊溟,姜虹,贠敏,等.大型复杂曲面类毛坯加工定位的全局优化算法[J].系统仿真学报, 2005(4):825-826.

MA LiMing, JIANG Hong ,YUN Min, et al. A global optimization algorithm of localization for huge sculpture surface blank[J]. Journal of System Simulation, 2005(4):825-826.

[7] 严思杰,周云飞,赖喜德,等.基于曲面重构方法的大型叶片加工定位问题研究[J].机床与液压, 2006(3): 9-12.

YAN Sijie, ZHOU Yunfei, LAI Xide, et al. Research on the localization of large blade NC machining based on the surface reconstruction[J]. Machine Tool &Hydraulics, 2006(3): 9-12.

[8] Besl P J, McKay N D. A method for registration of 3D shapes[J].IEEE Transactions on Pattern Analysis Machine Intelligence,1992,14(2):239-256．

[9] 董明晓,郑康平,许伯彦,等. 一种快速求取空间点到曲面最短距离的算法[J]. 组合机床与自动化加工技术, 2004(9):11-12.

DONG Mingxiao, ZHENG Kangping, XU Boyan, et al. An algorithm for quickly calculating the minimum distance between a space point and a surface[J]. Modular Machine Tool & Automatic Manufacturing Technique,2004(9):11-12.

[10] 徐汝峰,陈志同,陈五一. 计算点到曲面最短距离的网格法[J]. 计算机集成制造系统, 2011(1):95-100.

XU Rufeng, CHEN Zhitong, CHEN Wuyi. Grid algorithm for calculating the shortest distance from spatial point to free-form surface[J].Computer Integrated Manufacturing Systems, 2011(1): 95-100.